Using CEBRA-Time to Identify Latent Embeddings

In this notebook, we will explore the applications of the advanced machine learning algorithm, CEBRA (created by the Mathis Laboratory), to analyze OpenScope data from the Allen Institute. CEBRA is an algorithm that optimizes neural networks that map neural activity onto an embedding space [Schneider et al., 2023]. This algorithm leverages contrastive learning and a generalized InfoNCE loss function to learn representations where similar data points are pulled closer together while dissimilar data points are pushed apart within the embedding space. CEBRA has three different modes: CEBRA-Time (fully unsupervised/self supervised), CEBRA-Behavior (supervised), and CEBRA-Hybrid.

In this notebook, we will be utilizing CEBRA-Time, so our input data will be unlabeled and there will be no behavioral assumptions that influence neuronal activity. We utilize CEBRA-Time to create a 3D latent embedding space of a mouse’s neural activity while passively viewing visual stimuli. This algorithm can help us identify patterns in neural activity and its relationship to the visual stimulus. We use the neural data to train the model, generate embeddings for each type of visual stimulus, and plot different subsections of the data separately onto the same embedding space.

Below is a visualization of the pipeline that displays the steps from how the algorithm receives input data to how the final output of the embedding is produced. To briefly describe how it works, CEBRA takes input in the form of positive and negative pairs of data relative to a reference point. An example of a positive and negative pair for behavioral labels would be two positions on a track that are close together in space versus a position on a track that is far away. Likewise, for time labels, a positive pair would be data from two points that occur close together in time versus a data point that occurs farther away in time. Next, a nonlinear encoder receives the data in the form of a triplet that contains 3 vectors: neural data from the positive points, neural data from the negative points, and neural data from the reference points. The nonlinear encoder maps the raw neural data onto a lower dimensional feature space. Here, CEBRA leverages contrastive learning to learn representations where similar pairs are pulled closer together and dissimilar pairs are pushed apart in an embedding space. During training, similarity scores are computed for positive and negative pairs. A modified InfoNCE loss function is calculated and gradient descent is used to optimize the loss. Once the network is fully trained, the lower-dimensional embedding space is produced from the final output layer.

For further details on CEBRA, you can refer to the paper published by the Mathis Lab or visit the CEBRA website to gain a deeper understanding on these concepts. Understanding how the input data is processed is important as well as how each point in the embedding relates to a given input.

Additionally, in this notebook, we will be using open source data published by the Allen Institute titled Measuring Stimulus-Evoked Neurophysiological Differentiation in Distinct Populations of Neurons in Mouse Visual Cortex. This study employs two-photon calcium imaging to study stimulus-evoked neuronal response in excitatory neurons in five different visual cortical areas. Recordings were taken from mice during passive viewing of either naturalistic or phase-scrambled movie stimuli. During the viewing, each stimulus type was repeated 10 times, nonconsecutively. Our objective is to use CEBRA to generate an embedding space that is consistent across movie repeat. Essentially, we aim to extract a representation of the movie that could be present in the neuronal activity across all repeats.

Figure 1a, Learnable latent embeddings for joint behavioural and neural analysis

Notebook Settings for Google Colab

To ensure the fastest and runtime, check to make sure your hardware accelerator is using GPU. This should be pre-set for the notebook, but here are the steps to double-check it is set correctly:

1. click “Edit” below the notebook title

2. near the bottom of the list click “Notebook settings”

3. In the “Hardware Accelerator” dropdown, click “GPU”

4. select the “GPU type” that you please

5. click “Save” and run the notebook

Create CEBRA Environment and Download Dependencies

⚠️Note: If running on a new environment, run this cell once and then restart the kernel⚠️

import warnings
warnings.filterwarnings('ignore')

try:
    from databook_utils.dandi_utils import dandi_download_open
except:
    !git clone https://github.com/AllenInstitute/openscope_databook.git
    %cd openscope_databook
    %pip install -e .

import cebra
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from cebra import CEBRA

%matplotlib inline

Download Data

We download the data using the same process as in previous notebooks. If you need help downloading OpenScope data, see the Downloading an NWB File notebook.

# download ophys files
dandiset_id = "000036"
dandi_filepath = "sub-389014/sub-389014_ses-20180705T152908_behavior+image+ophys.nwb"
download_loc = "."
dandi_api_key = None

# download data
io = dandi_download_open(dandiset_id, dandi_filepath, download_loc, dandi_api_key=dandi_api_key)
nwb = io.read()

PATH                                                    SIZE   DONE            DONE% CHECKSUM STATUS          MESSAGE
sub-389014_ses-20180705T152908_behavior+image+ophys.nwb 1.3 GB 1.3 GB           100%    ok    done                   
Summary:                                                1.3 GB 1.3 GB                         1 done                 
                                                               100.00%                                               
Downloaded file to ./sub-389014_ses-20180705T152908_behavior+image+ophys.nwb
Opening file

Setting Up The Stimulus Table

The stimulus table below includes information about the type of visual stimulus that was presented to the mice during the passive viewing experiment. It contains the start and stop time for each presentation of a frame, the frame number, and the stimulus type. The frame number helps us to identify the exact part of the movie the mouse is viewing. Before proceeding with the rest of the code, it’s advisable to become familiar with the stimulus table and the data it contains. Understanding the structure and content of the stimulus table will help with comprehending the subsequent code.

The function stim_obj_to_table retrieves start_times, stop_times, frames, and stim-type from an NWB file and then organizes that data into a pandas dataframe. Pandas dataframes are a very useful way to organize, manipulate, and explore data.

# use this if nwb intervals section has no stim information
def stim_obj_to_table(nwb):

    all_labeled_stim_timestamps = []
    for stim_type, stim_obj in nwb.stimulus.items():
        start_times = stim_obj.timestamps[:-1]
        stop_times = stim_obj.timestamps[1:]
        frames = stim_obj.data[:-1]
        l = len(start_times)
        labeled_timestamps = list(zip(start_times, stop_times, frames, [stim_type]*l))
        all_labeled_stim_timestamps += labeled_timestamps

    all_labeled_stim_timestamps.sort(key=lambda x: x[0])
    stim_table = pd.DataFrame(all_labeled_stim_timestamps, columns=("start time", "stop time", "frame", "stimulus type"))

    return stim_table

stim_table = stim_obj_to_table(nwb)

# view the stimulus table
stim_table

	start time	stop time	frame	stimulus type
0	27.475720	27.492416	0	spontaneous
1	27.492416	27.509112	0	spontaneous
2	27.509112	27.525758	0	spontaneous
3	27.525758	27.542211	0	spontaneous
4	27.542211	27.559146	0	spontaneous
...	...	...	...	...
241181	4231.635599	4231.652274	897	snake
241182	4231.652274	4231.668936	897	snake
241183	4231.668936	4231.685619	898	snake
241184	4231.685619	4231.702325	898	snake
241185	4231.702325	4231.718994	899	snake

241186 rows × 4 columns

Extracting DFF Data

The neural data we are trying to analyze is contained in a 2D array called dff_trace and has a shape of (127117, 41) – this will vary for different datasets. From the shape, we can tell that there are 41 regions of interest (or neurons) and 127177 measurements of fluorescence for each neuron. This will produce a matrix with 127177 rows and 41 columns. Each of the 127177 measurements are taken at the same time for each neuron. For example, [5][0] (first ROI 6th measurement) will have a different fluorescence value than [5][33] (34th ROI, 6th measurement) but these measurements will have been taken at the same time during the trial. The timestamps for each fluorescence value are contained in the dff_timestamps array that should have the same length as dff_trace.

# access the data we want
dff = nwb.processing["ophys"]["DfOverF"]
dff_trace = np.array(dff.roi_response_series["imaging_plane_1"].data).transpose()
dff_timestamps = dff.roi_response_series["imaging_plane_1"].timestamps[:-1]

print(dff_trace.shape)
print(dff_timestamps.shape)

(127177, 41)
(127177,)

Aligning Different Types of Data

Currently, we have data from the stimulus table and neural data collected during the 2P imaging. Since the data is from two different places, it is essential to make sure they are aligned by time. The data from the stimulus table includes the start and stop time of each frame of the visual stimulus, the frame number, and the type of visual stimulus that is presented. The purpose of the code below is to identify a frame number and stimulus type for each value in dff_timestamps. Once we have the timestamps aligned with the data in the stimulus table, we can properly index and label the fluorescence traces from dff_traces that will be inputted into CEBRA-Time.

# retrieve intervals of time associated with each frame
frame_intervals = []
frame_list = []
stim_type_list = []

frame_start = stim_table["start time"][0]
frame_end = stim_table["stop time"][0]

for i in range(len(stim_table)):
    if i+1 == len(stim_table):
        continue
    current_frame = stim_table["frame"][i]
    next_frame = stim_table["frame"][i + 1]
    next_start_time = stim_table["start time"][i+1]
    next_stop_time = stim_table["stop time"][i+1]
    current_stim = stim_table["stimulus type"][i]
    next_stim = stim_table["stimulus type"][i+1]

    # appends the start and stop time for each individual frame to get a list of frame intervals
    if current_frame != next_frame or current_stim != next_stim:
        frame_end = next_start_time
        frame_intervals.append((frame_start, frame_end))
        frame_list.append(current_frame)
        stim_type_list.append(current_stim)
        frame_start, frame_end = next_start_time, next_stop_time

# now we can identify the interval of time each frame is displayed
print(len(frame_intervals))
print(len(frame_list))

136798
136798

In the following cell, the two lists timestamp_frames and timestamp_stimulus will be appended to contain the visual movie frames and the stimulus type for each point in the dff_timestamps array. After the while-loop is complete, we will have a list of frames and stimulus types and should be aligned with the dff_timestamps array. This is useful for indexing later in the notebook.

# matches each timestamp from 'dff_timestamps' with its corresponding frame in 'frame_list'
i, j = 0, 0
timestamp_frames =  [] # will contain list of frames associated with each timestamp
timestamp_stimulus = [] # will contain list of stimulus type associated with each timestamp
count_times_before_stim = 0

while i < len(dff_timestamps) and j < len(frame_intervals):
    this_timestamp = dff_timestamps[i]
    start_time, stop_time = frame_intervals[j]
    this_stimulus = stim_type_list[j]
    this_frame = frame_list[j]

    if this_timestamp >= start_time and this_timestamp <= stop_time:
        timestamp_frames.append(this_frame)
        timestamp_stimulus.append(this_stimulus)
        i += 1
    elif this_timestamp < start_time:
        i += 1
        count_times_before_stim += 1
    else:
        j += 1

Here, we run into an issue: timestamp_frames and timestamp_stimulus have a different length than dff_timestamps. This means that if we try to index a timestamp using an index value from the frames list, it will correspond with the wrong timestamp value. When comparing the stimulus table to the timestamps array, total time in seconds from the stimulus table is less than the total time accounted for in dff_timestamps, meaning there are some timestamps that do not correspond with any frame or any stimulus type. In other words, some timestamps occur before or after the duration of stimulus presentation. To correctly align the data, we need to slice dff_timestamps to only include timestamps that correspond with a visual stimulus.

# the length of timestamp_frames is different than the length of dff_timestamps and we need to figure out why
print(len(timestamp_frames))
print(len(timestamp_stimulus))
print(len(dff_timestamps))

print("Number of timestamps unaccounted for: ", len(dff_timestamps)-len(timestamp_frames))

126758
126758
127177
Number of timestamps unaccounted for:  419

# number of dff_timestamps that occur before the first frame is presented (while timestamp < start_time)
print("Number of timestamps that occur before stimulus:", count_times_before_stim)

# find how many dff_timestamps occur after the last visual stimulus is displayed
max_frame_time = np.max(frame_intervals)
max_timestamp_allowed = np.where(dff_timestamps > max_frame_time)[0][0]

# find the last timestamp that occurs during stimulus presentation
timestamps_before_stim_end = len(dff_timestamps) - (len(dff_timestamps)- max_timestamp_allowed)
print("Last timestamp that occurs during stimulus presentation:", timestamps_before_stim_end)

# slice `dff_timestamps` to only include timestamps that correlate with frames
sliced_dff_timestamps = dff_timestamps[count_times_before_stim:timestamps_before_stim_end]
print("New length of dff_timestamps:", len(sliced_dff_timestamps))

# this aligns the dff_trace with sliced version of the dff_timestamps so that we can correctly index the neural data
sliced_dff_trace = dff_trace[count_times_before_stim:timestamps_before_stim_end]
print("New length of dff_trace:", len(sliced_dff_trace))

Number of timestamps that occur before stimulus: 133
Last timestamp that occurs during stimulus presentation: 126891
New length of dff_timestamps: 126758
New length of dff_trace: 126758

Now that all of our data is aligned by time and shape, we can create a 2D array that includes each timestamp and its correlated frame number and stimulus type. While this array might not be directly useful for CEBRA-Time, it can be useful in the future for CEBRA-Behavior, and can easily be converted to a pandas dataframe.

timestamp_frames = np.asarray(timestamp_frames)
timestamp_stimulus = np.asarray(timestamp_stimulus)

# produces a 2D array with dff_timestamps, frame number, and stim type
times_frames_stimtype = np.stack((sliced_dff_timestamps, timestamp_frames, timestamp_stimulus))
times_frames_stimtype = np.transpose(times_frames_stimtype)
print(times_frames_stimtype.shape)
print(times_frames_stimtype)

(126758, 3)
[['27.47572' '0' 'spontaneous']
 ['27.50889' '0' 'spontaneous']
 ['27.54205' '0' 'spontaneous']
 ...
 ['4231.61079' '896' 'snake']
 ['4231.64396' '897' 'snake']
 ['4231.67713' '898' 'snake']]

Perform a GRID-search for training hyper parameters

This algorithm training code was borrowed from the Demo Hypothesis Testing Notebook provided by the Mathis Lab, the creators of CEBRA. If you are interested in the specifics of how the network is trained in the code below, you can view the documentation on the CEBRA website.

CEBRA provides a number of degrees of freedom to optimize the final embedding. It is important that you use a set of parameters that produce consistent embeddings with low reconstruction losses. To fine-tune these parameters, CEBRA provides functionalities to perform a grid-search. Below, we provide example code to look for an optimal set of parameters for a dataset. Keep in mind that making sure this selection generalizes well to new datasets is important to avoid over-fitting. This search is rather intensive, so it is recommended to run this on a good machine. We found that the T4 units on DandiArchive were fairly goods at the moment and would run this search in less than an hour.

# First you define the parameter to explore. Here we explore the output dimension, learning rate, time offset, and model num_hidden_units.
params_grid = dict(
    output_dimension = [16, 32, 64, 128],
    learning_rate = [0.001, 0.01, 0.0003],
    time_offsets = [10, 20],
    model_architecture="offset10-model",
    batch_size=512,
    temperature_mode="constant",
    max_iterations=[1000], # we initially set this low to limit computation and will increase it later to fully train the best model
    distance="cosine",
    conditional="time",
    device="cuda_if_available",
    num_hidden_units = [32, 64, 128],
    temperature=1,
    verbose = True)

# we construct the input data
datasets = {"dataset1": sliced_dff_trace} # a different set of data

# we run the grid search
grid_search = cebra.grid_search.GridSearch()
grid_search.fit_models(datasets=datasets, params=params_grid, models_dir="saved_models")

pos: -0.7285 neg:  6.3555 total:  5.6269 temperature:  1.0000: 100%|██████████| 1000/1000 [00:20<00:00, 48.22it/s]
pos: -0.6524 neg:  6.3869 total:  5.7345 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.38it/s]
pos: -0.7379 neg:  6.3612 total:  5.6233 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 73.50it/s]
pos: -0.6438 neg:  6.3600 total:  5.7162 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 73.71it/s]
pos: -0.7321 neg:  6.3526 total:  5.6205 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 72.67it/s]
pos: -0.6508 neg:  6.3613 total:  5.7105 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 73.28it/s]
pos: -0.7400 neg:  6.3647 total:  5.6248 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 72.62it/s]
pos: -0.6315 neg:  6.3695 total:  5.7380 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.90it/s]
pos: -0.7498 neg:  6.3446 total:  5.5948 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.97it/s]
pos: -0.6573 neg:  6.3502 total:  5.6928 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 71.60it/s]
pos: -0.7606 neg:  6.3482 total:  5.5876 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 74.04it/s]
pos: -0.6637 neg:  6.3682 total:  5.7045 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 72.65it/s]
pos: -0.7475 neg:  6.3576 total:  5.6102 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 72.79it/s]
pos: -0.6764 neg:  6.3614 total:  5.6850 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 72.77it/s]
pos: -0.7496 neg:  6.3437 total:  5.5941 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 71.86it/s]
pos: -0.6635 neg:  6.3616 total:  5.6982 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.12it/s]
pos: -0.7607 neg:  6.3441 total:  5.5834 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.33it/s]
pos: -0.6636 neg:  6.3628 total:  5.6992 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.45it/s]
pos: -0.7591 neg:  6.3456 total:  5.5865 temperature:  1.0000: 100%|██████████| 1000/1000 [00:18<00:00, 53.21it/s]
pos: -0.6539 neg:  6.3588 total:  5.7049 temperature:  1.0000: 100%|██████████| 1000/1000 [00:18<00:00, 52.81it/s]
pos: -0.7599 neg:  6.3430 total:  5.5831 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 52.45it/s]
pos: -0.6830 neg:  6.3534 total:  5.6704 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.89it/s]
pos: -0.7542 neg:  6.3418 total:  5.5876 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.29it/s]
pos: -0.6856 neg:  6.3519 total:  5.6663 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.68it/s]
pos: -0.7837 neg:  6.3548 total:  5.5711 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.39it/s]
pos: -0.6663 neg:  6.3573 total:  5.6909 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.70it/s]
pos: -0.7663 neg:  6.3572 total:  5.5909 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 71.43it/s]
pos: -0.6958 neg:  6.3610 total:  5.6653 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 69.48it/s]
pos: -0.7704 neg:  6.3520 total:  5.5816 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.63it/s]
pos: -0.6863 neg:  6.3700 total:  5.6837 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.49it/s]
pos: -0.7863 neg:  6.3583 total:  5.5721 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.08it/s]
pos: -0.6893 neg:  6.3875 total:  5.6982 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.75it/s]
pos: -0.8001 neg:  6.3477 total:  5.5476 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 67.22it/s]
pos: -0.7508 neg:  6.3592 total:  5.6083 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.55it/s]
pos: -0.7983 neg:  6.3520 total:  5.5536 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.40it/s]
pos: -0.7565 neg:  6.3960 total:  5.6395 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.35it/s]
pos: -0.7942 neg:  6.3522 total:  5.5580 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 69.99it/s]
pos: -0.7510 neg:  6.3753 total:  5.6243 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.87it/s]
pos: -0.7943 neg:  6.3477 total:  5.5534 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.09it/s]
pos: -0.7319 neg:  6.3581 total:  5.6262 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 69.34it/s]
pos: -0.8235 neg:  6.3555 total:  5.5320 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.31it/s]
pos: -0.7812 neg:  6.3793 total:  5.5982 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.15it/s]
pos: -0.8226 neg:  6.3462 total:  5.5236 temperature:  1.0000: 100%|██████████| 1000/1000 [00:18<00:00, 52.63it/s]
pos: -0.8091 neg:  6.3769 total:  5.5678 temperature:  1.0000: 100%|██████████| 1000/1000 [00:18<00:00, 53.14it/s]
pos: -0.8429 neg:  6.3507 total:  5.5078 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.71it/s]
pos: -0.7983 neg:  6.4004 total:  5.6021 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.78it/s]
pos: -0.8487 neg:  6.3547 total:  5.5060 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.55it/s]
pos: -0.7959 neg:  6.3768 total:  5.5809 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.51it/s]
pos: -0.6838 neg:  6.3583 total:  5.6745 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.57it/s]
pos: -0.5868 neg:  6.3768 total:  5.7900 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.54it/s]
pos: -0.6826 neg:  6.3617 total:  5.6790 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 71.00it/s]
pos: -0.6093 neg:  6.3637 total:  5.7544 temperature:  1.0000: 100%|██████████| 1000/1000 [00:13<00:00, 71.67it/s]
pos: -0.6779 neg:  6.3539 total:  5.6760 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.84it/s]
pos: -0.5971 neg:  6.3657 total:  5.7686 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.58it/s]
pos: -0.6904 neg:  6.3562 total:  5.6659 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 67.96it/s]
pos: -0.5910 neg:  6.3814 total:  5.7904 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.65it/s]
pos: -0.7042 neg:  6.3518 total:  5.6475 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.33it/s]
pos: -0.6020 neg:  6.3582 total:  5.7561 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 69.75it/s]
pos: -0.7258 neg:  6.3563 total:  5.6305 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.79it/s]
pos: -0.5988 neg:  6.3527 total:  5.7539 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.96it/s]
pos: -0.7037 neg:  6.3541 total:  5.6504 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 70.91it/s]
pos: -0.6039 neg:  6.3698 total:  5.7658 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 69.70it/s]
pos: -0.7086 neg:  6.3623 total:  5.6537 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.76it/s]
pos: -0.5915 neg:  6.3592 total:  5.7677 temperature:  1.0000: 100%|██████████| 1000/1000 [00:14<00:00, 68.11it/s]
pos: -0.7306 neg:  6.3523 total:  5.6217 temperature:  1.0000: 100%|██████████| 1000/1000 [00:20<00:00, 49.88it/s]
pos: -0.5935 neg:  6.3619 total:  5.7684 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.39it/s]
pos: -0.7273 neg:  6.3436 total:  5.6163 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 52.42it/s]
pos: -0.6309 neg:  6.3486 total:  5.7177 temperature:  1.0000: 100%|██████████| 1000/1000 [00:18<00:00, 53.23it/s]
pos: -0.7479 neg:  6.3490 total:  5.6010 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.30it/s]
pos: -0.6594 neg:  6.3631 total:  5.7037 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 51.99it/s]
pos: -0.7496 neg:  6.3519 total:  5.6023 temperature:  1.0000: 100%|██████████| 1000/1000 [00:20<00:00, 49.96it/s]
pos: -0.6272 neg:  6.3584 total:  5.7312 temperature:  1.0000: 100%|██████████| 1000/1000 [00:19<00:00, 50.85it/s]

<cebra.grid_search.GridSearch at 0x7a3889de9a50>

You can access the underlying grid-search object to visualise the best set of parameters. The models are saved in a “saved_models” folder along with the notebook.

df_results = grid_search.get_df_results(models_dir="saved_models")
best_model, best_model_name = grid_search.get_best_model(dataset_name="dataset1", models_dir="saved_models")

This is the distribution of loss values obtained at the end of training.

# Get all the final losses
pd_loss = grid_search.get_df_results()

# Plot the losses for each parameter combination in a bar plot
# The y-axis is the parameter combination and the x-axis is the loss
# We combine the parameters into a single string for the x-axis
pd_loss["params"] = pd_loss["learning_rate"].astype(str) + "_" + pd_loss["num_hidden_units"].astype(str) + "_" + pd_loss["output_dimension"].astype(str) + "_" + pd_loss["time_offsets"].astype(str)
pd_loss_sorted = pd_loss.sort_values(by="loss", ascending=False)
pd_loss_sorted.plot.barh(x="params", y="loss", figsize=(10, 20))

# We turn off the legend from the plot
plt.gca().legend_.remove()

best_model

CEBRA(batch_size=512, conditional='time', learning_rate=0.01,
      max_iterations=1000, model_architecture='offset10-model',
      num_hidden_units=128, output_dimension=128, temperature=1,
      time_offsets=10, verbose=True)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

best_model_name

'learning_rate_0.01_num_hidden_units_128_output_dimension_128_time_offsets_10_dataset1'

Train CEBRA-Time Model

Here, we use our insight from the grid-search to fully train the CEBRA model using the neural data (sliced_dff_trace). Training the model can take anywhere from a few minutes to a few hours depending on the size of the dataset you are inputting. If you want to lower CPU usage, or if you want to experiment quickly with the model, it’s best to either use a smaller slice of the data you input, or lower the number of max iterations. Keep in mind, this will lower the quality of the embedding space.

# alter the number of max_iterations to get a faster runtime
max_iterations = 20000 # default is 5000

# set conditional to 'time'
cebra_time_model = CEBRA(model_architecture="offset10-model",
                        batch_size=512,
                        learning_rate=1e-2,
                        temperature=1,
                        output_dimension=16,
                        num_hidden_units=128,
                        max_iterations=max_iterations,
                        distance="cosine",
                        conditional="time",
                        device="cuda_if_available",
                        verbose=True,
                        time_offsets=10)

# insert the data you want to train in .fit()
cebra_time_model.fit(sliced_dff_trace)
cebra_time_model.save("cebra_time_model.pt")

pos: -0.9630 neg:  6.2982 total:  5.3351 temperature:  1.0000: 100%|██████████| 20000/20000 [06:24<00:00, 51.97it/s]

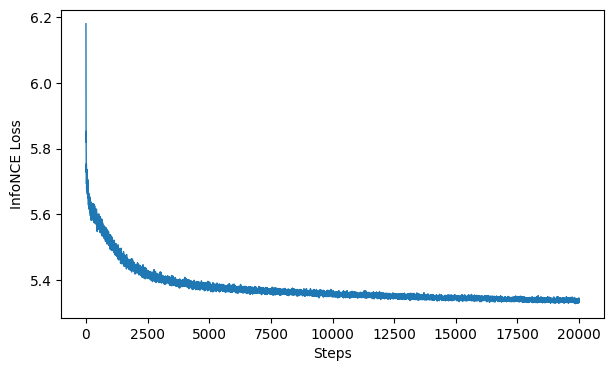
Evaluate The Loss

Here, we plot the loss function of the algorithm. CEBRA uses the InfoNCE loss function to serve as a goodness-of-fit metric to the data, and helps determine which variables have the largest influence on the data. The goal is to minimize loss, so if your network is well trained, you should see a low loss value. Typically, a loss value less than 7 indicates the model is well train on the data.

# this plots the loss from the model we saved in the previous cell
cebra.plot_loss(cebra_time_model, color = "tab:blue")

<AxesSubplot: xlabel='Steps', ylabel='InfoNCE Loss'>

Produce Embedding Spaces for CEBRA-Time

Now, we want to determine if CEBRA-Time can produce a clear embedding space for our data. For this dataset, when we plotted all the points of neural data onto one embedding space, it was difficult to visually detect patterns in the data. A solution to this problem is to create many different plots of the same embedding space that contain different sections of the data. Below, we separate our neural data by stimulus type and then for each stimulus type, we plot each repeat of the movie separately onto the embedding space. We also color the points on the embedding space based on the movie frame. This means that frames that are shown close together in time will have similar colors. For reference, there are 10 repeats of each stimulus type (except for dots), and each repeat contains 899 frames. We have also excluded three stimulus types (‘snake’, ‘noise’, and ‘spontaneous’) from the plots because they did not repeat, or contained issues within the repeats. The hope is that each repeat of each movie will be plotted similarly onto the embedding space, and ultimately, each stimulus type will be differentiable when plotted onto one large embedding space.

First, we create a function that selects neural data based on one repeat of the movie. We index the neural data with the indices of a particular movie repeat, and then load that indexed neural data into the trained CEBRA model which will be used to produce one plot of the embedding space. We also index the frames associated with each point of neural data based on the same indices, and use the value of each frame to create color labels for the embedding space. Next, we create a function that plots each model separately. In the following cell, we use a for-loop to loop through each stimulus, and within that stimulus, we loop through each repeat. For each repeat, we call the two functions and are able to produce a plot of the embedding space for that specific slice of data.

### inputs fluorescence traces for each repeat of the stimulus into the model and gets colors for embedding space
### returns an embedding space of points and color labels for each point
def get_embeddings(selected_frames, individual_dff_input, movie_repeat_indices):

    # takes fluorescence traces from particular stimulus interval and selects only traces for one specific repeat
    movie_repeat_input = individual_dff_input[movie_repeat_indices]

    # inputs neural data for each individual repeat into model
    cebra_time_model = cebra.CEBRA.load("cebra_time_model.pt")
    cebra_time = cebra_time_model.transform(movie_repeat_input)

    # create color labels for embedding
    color_labels = []
    # takes frames of visual movie for a particular stimulus and selects only frames from a specific repeat of the movie
    repeat_frames = selected_frames[movie_repeat_indices]
    for frame in repeat_frames:
        total_frames = np.max(repeat_frames)
        # allows frames that are close together in time to be colored similarly
        value = frame/total_frames
        color_labels.append(value)

    color_labels = np.asarray(color_labels)
    return cebra_time, color_labels

### plots embedding space for one repeat of the visual stimulus
def create_subplots(cebra_time_models_list, cebra_embedding_colors_list):
    fig = plt.figure(figsize=(20, 7))

    plt.title(f"CEBRA-Time - {stim_name}")
    plt.gca().axis("off")

    # We only plot a subset
    if len(cebra_time_models_list)>4:
        index_repeat = [0, 1, 4, 6, 9]
    else:
        index_repeat = range(len(cebra_time_models_list))

    # iterates through the list of cebra models and makes one plot for each model
    for i, value_index in enumerate(index_repeat):
        ax = fig.add_subplot(1, len(index_repeat), i+1, projection="3d")

        ax = cebra.plot_embedding(ax=ax, embedding=cebra_time_models_list[value_index], embedding_labels=cebra_embedding_colors_list[value_index], markersize=1, title=f"repeat {value_index}")

    return plt.show()

import sklearn

# provides the names of each stimulus type from the stim table
stimulus_names = set(stim_table["stimulus type"])

store_scores = {}
# loops through each stimulus type and selects the indices for every occurrence of that stimulus throughout the entire movie
for stim_name in stimulus_names:
    selected_indices = np.where(timestamp_stimulus == stim_name)[0]

    # excludes stimuli that do not exist or produce errors
    if len(selected_indices) == 0:
        print(f"{stimulus_names} not found")
    elif stim_name == "snake" or stim_name == "spontaneous":
        print("Invalid stim")
    # selects the visual movie frames and neural data for each different stimulus type
    else:
        selected_frames = timestamp_frames[selected_indices]
        individual_dff_input = sliced_dff_trace[selected_indices]

        movie_repeat_indices = []
        cebra_time_model_list = []
        cebra_embedding_colors_list = []

        # loops through each frame in the movie for a particular stimulus type and appends the index
        for i, frames in enumerate(selected_frames[:-1]):

            # We exclude the last frame of the movie that is repeated in the index due to edge conditions
            if frames<np.max(selected_frames):
                movie_repeat_indices.append(i)

            if selected_frames[i+1] == 0 or i == (len(selected_frames)-2):
                # use the function from above to get the cebra model and time embeddings for each repeat of the movie
                cebra_time, embedding_color_labels = get_embeddings(selected_frames, individual_dff_input, movie_repeat_indices)

                # append the model and embedding colors for each repeat to a list to be used in the plotting function
                cebra_time_model_list.append(cebra_time.copy())
                cebra_embedding_colors_list.append(embedding_color_labels.copy())

                movie_repeat_indices.clear()

        cebra_time_model_list = np.asarray(cebra_time_model_list, dtype=object)
        cebra_embedding_colors_list = np.asarray(cebra_embedding_colors_list, dtype=object)

        # use the function from above to create a plot of each model from the list we just made and color them using the corresponding embedding color list
        create_subplots(cebra_time_model_list, cebra_embedding_colors_list)

        # Parameter for KNN clustering
        nb_repeat = len(cebra_time_model_list)
        test_percent = 20.0
        nb_training = int(nb_repeat*(100.0-test_percent)/100.0)
        nb_test = int(nb_repeat*test_percent/100.0)

        # We only train a decoder if there are enough repeats.
        if nb_training>1 and nb_test>1:
            nb_folds = 10
            test_scores = []
            for index_fold in range(nb_folds):
                # Here we create the Decoder
                time_decoder = cebra.KNNDecoder(n_neighbors=300, metric="cosine")

                # We pick the folds randomly across repeats
                list_integers = np.arange(nb_repeat)
                list_test = np.random.choice(list_integers, nb_test, replace=False)

                # The following give the remaining integers
                list_training = np.setdiff1d(list_integers, list_test)

                # Extract training and testing data
                embedding_train = np.concatenate(cebra_time_model_list[list_training]).astype("float")
                label_train = np.concatenate(cebra_embedding_colors_list[list_training]).astype("float")

                # Fit the decoder
                time_decoder.fit(embedding_train, label_train)

                embedding_test = np.concatenate(cebra_time_model_list[list_test]).astype("float")
                label_test = np.concatenate(cebra_embedding_colors_list[list_test]).astype("float")

                # Measure performance on held out data
                time_pred = time_decoder.predict(embedding_test)

                local_test_score = sklearn.metrics.r2_score(label_test, time_pred)
                test_scores.append(local_test_score)

            # We average the folds
            average_test_score = np.mean(test_scores)

            # We store the result into a dictionary for later plotting
            print(f"Averaged R2 test score {average_test_score} for {stim_name}")
            store_scores[stim_name] = average_test_score

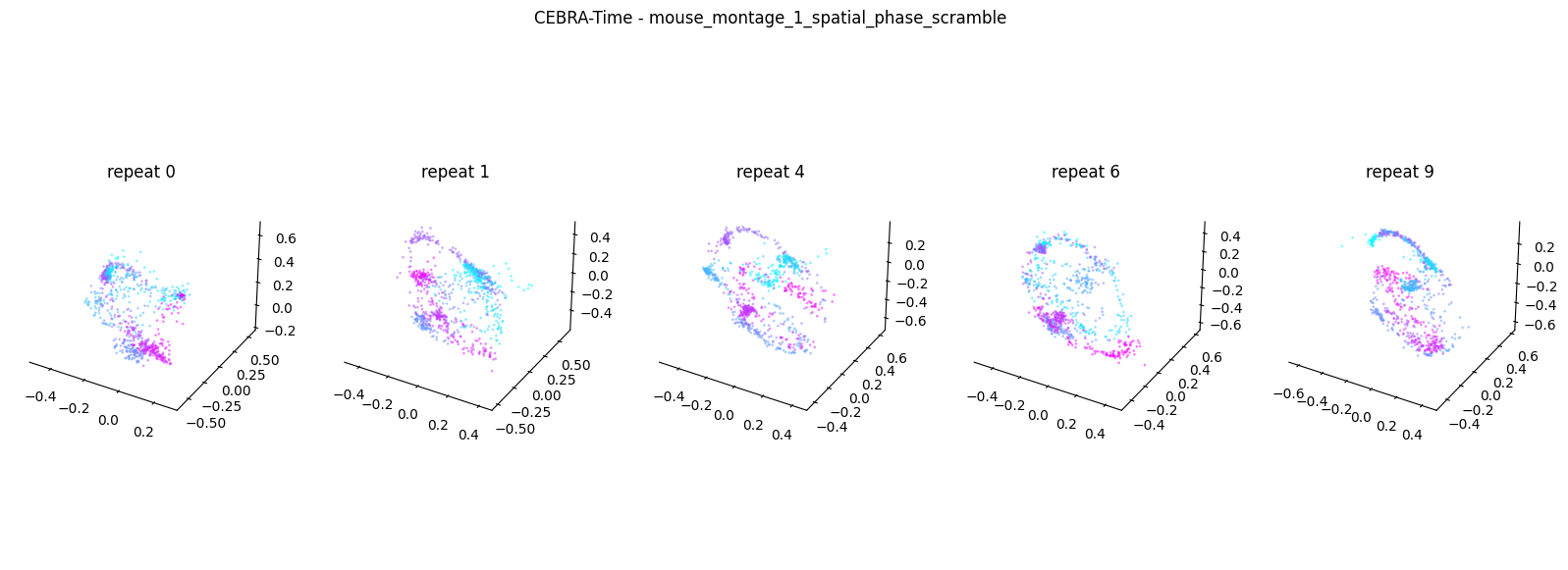
Averaged R2 test score 0.14665644996991373 for mouse_montage_1_spatial_phase_scramble

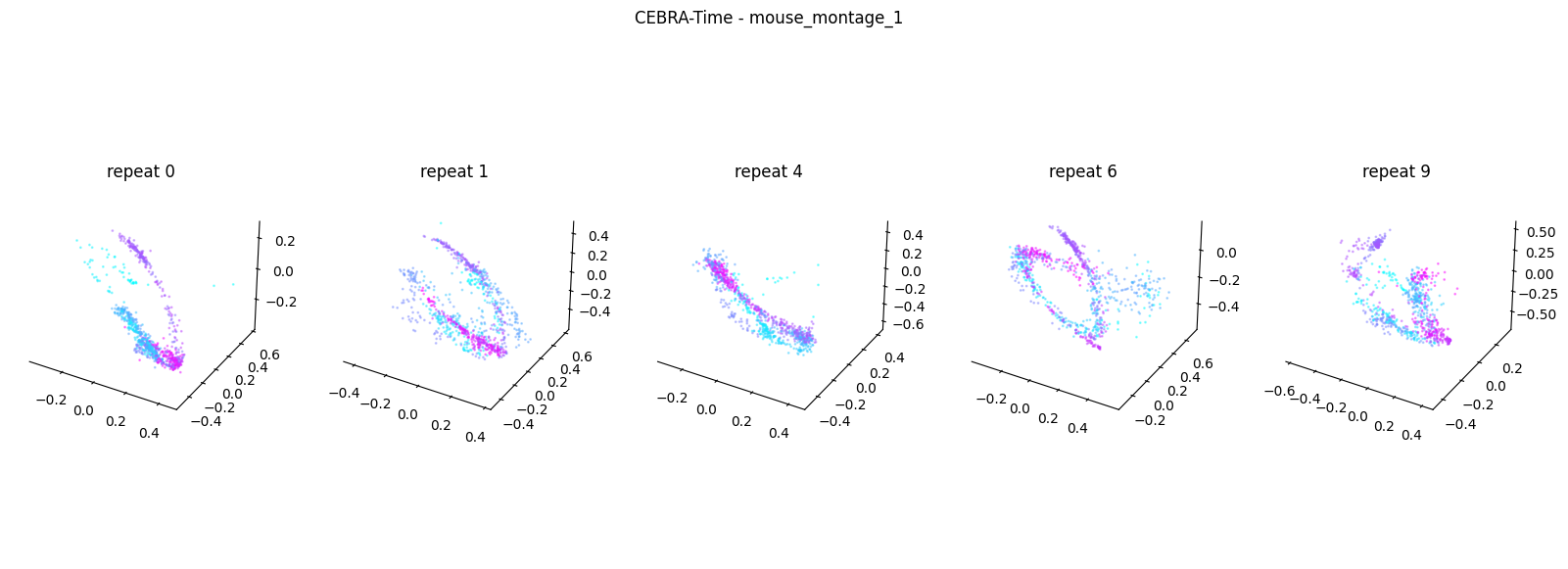
Averaged R2 test score 0.2913343281755714 for mouse_montage_1

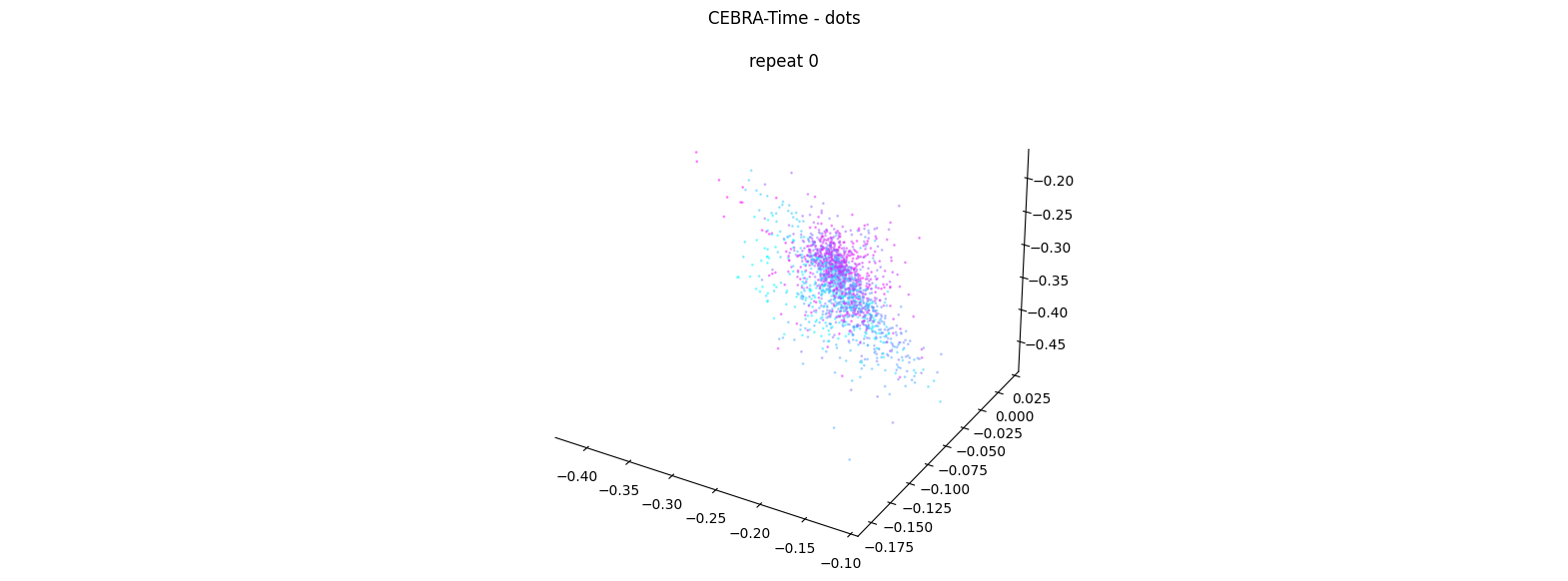
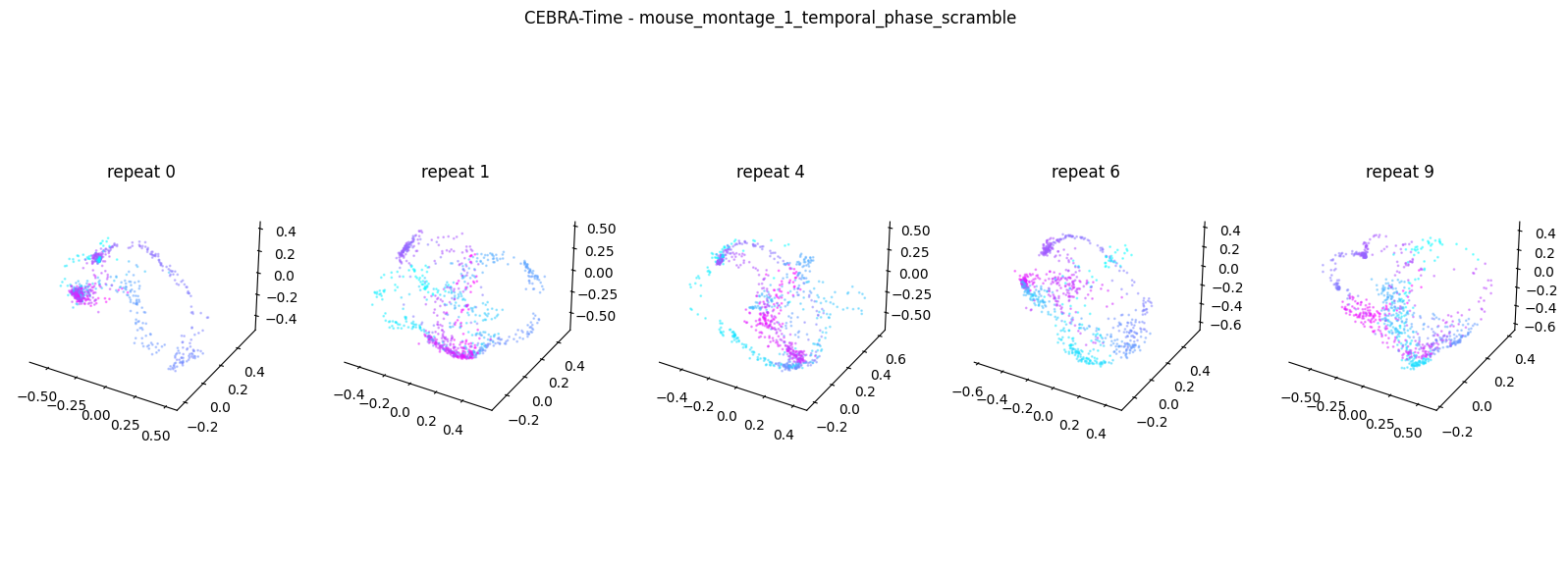
Averaged R2 test score -0.13274409534982662 for mouse_montage_1_temporal_phase_scramble
{'mouse_montage_1_spatial_phase_scramble', 'mouse_montage_1', 'dots', 'mouse_montage_1_temporal_phase_scramble', 'noise', 'conspecifics', 'crickets', 'mousecam', 'snake', 'mousecam_spatial_phase_scramble', 'human_montage', 'man_writing', 'spontaneous', 'mouse_montage_2'} not found

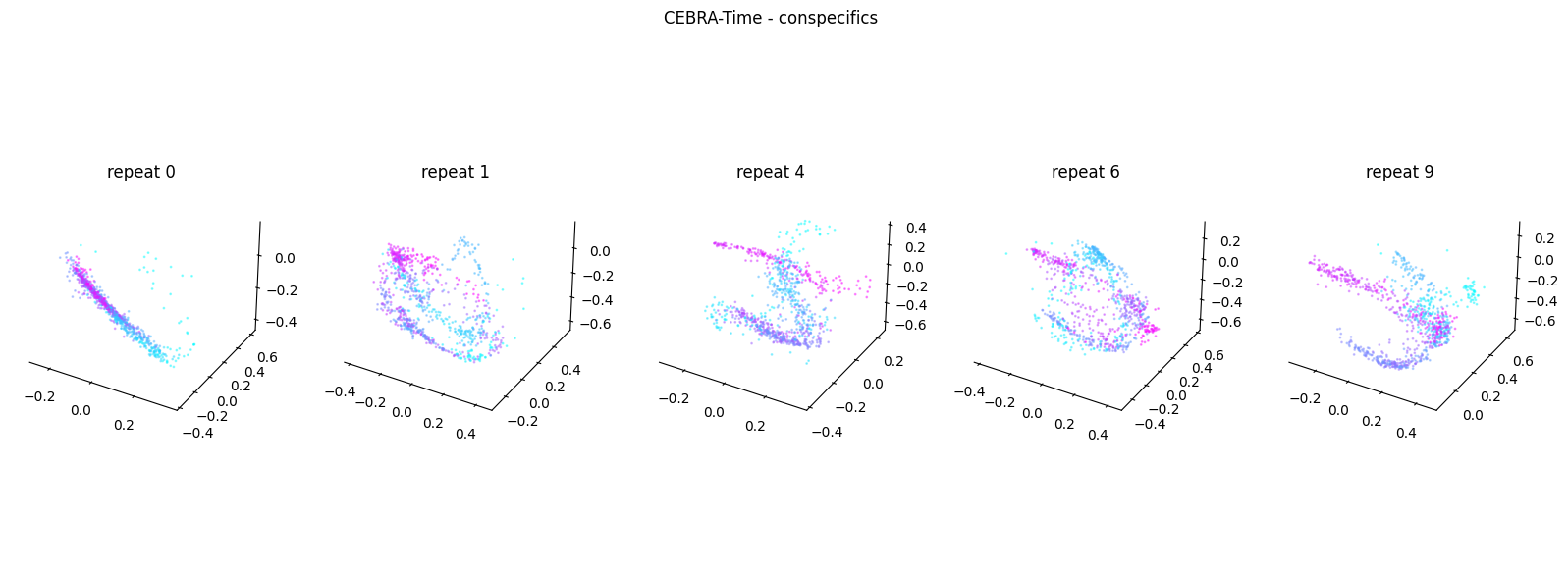
Averaged R2 test score 0.2639747381918638 for conspecifics

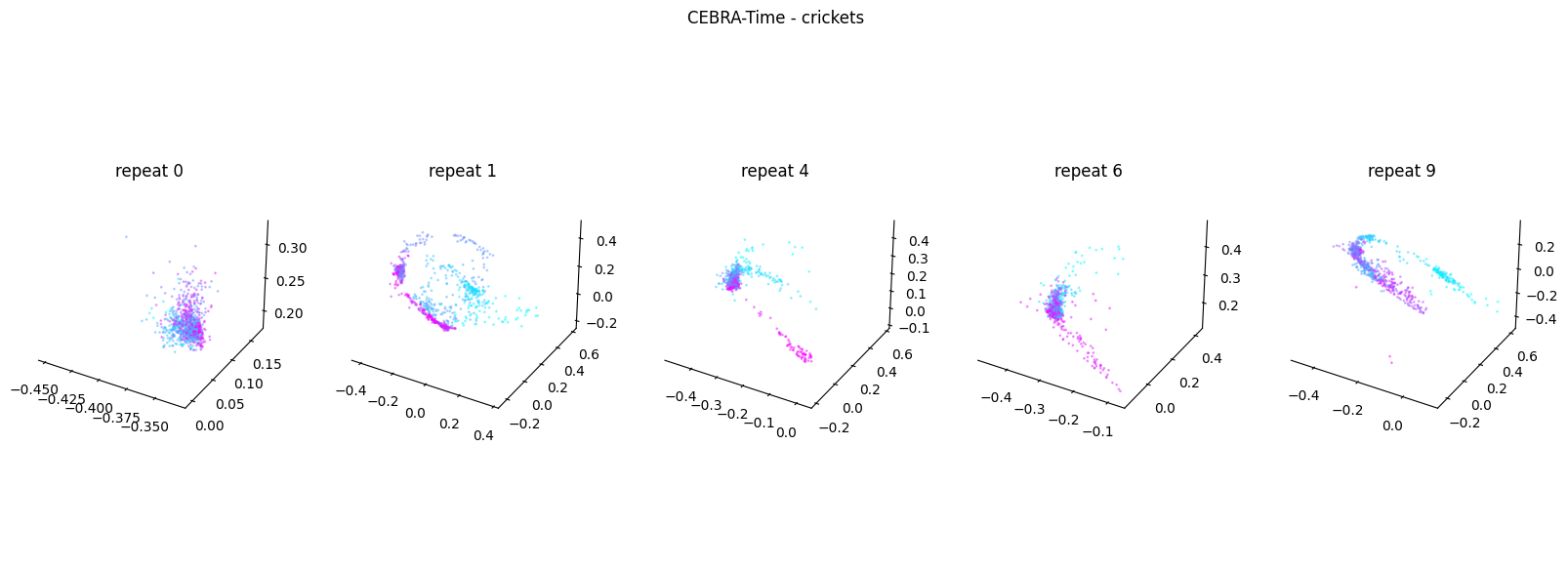
Averaged R2 test score 0.04141435202290535 for crickets

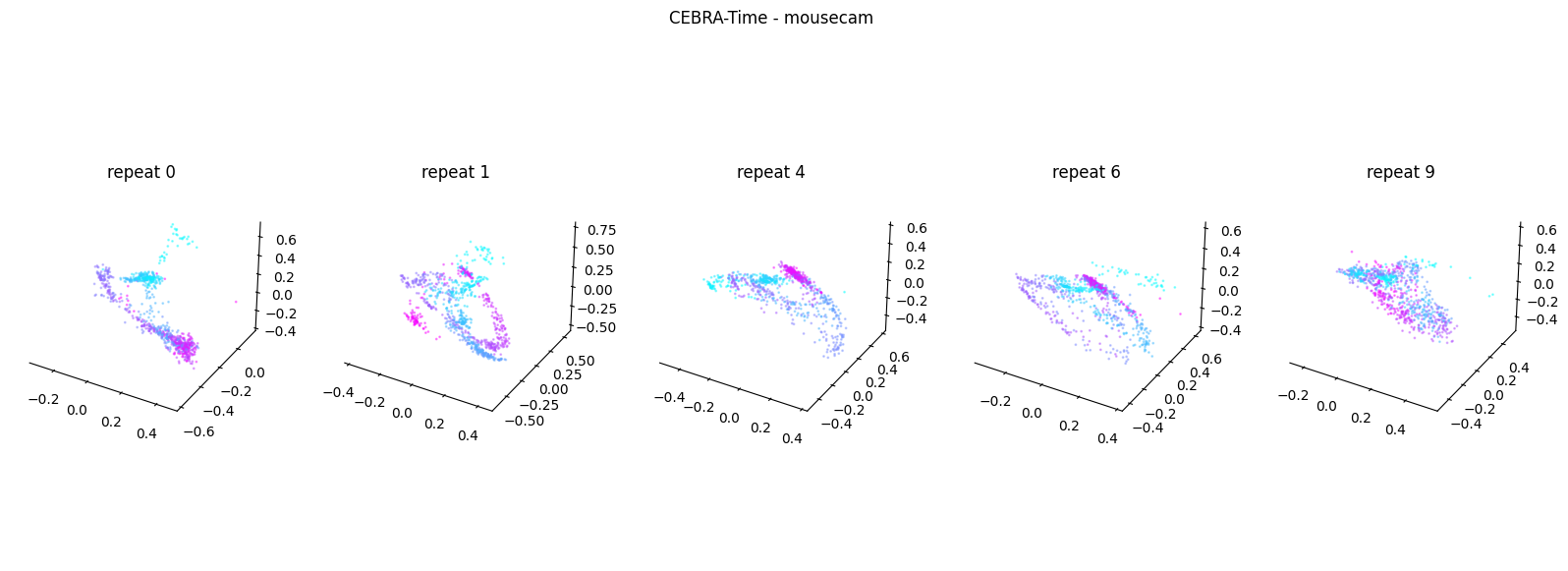
Averaged R2 test score 0.5125350100699715 for mousecam
Invalid stim

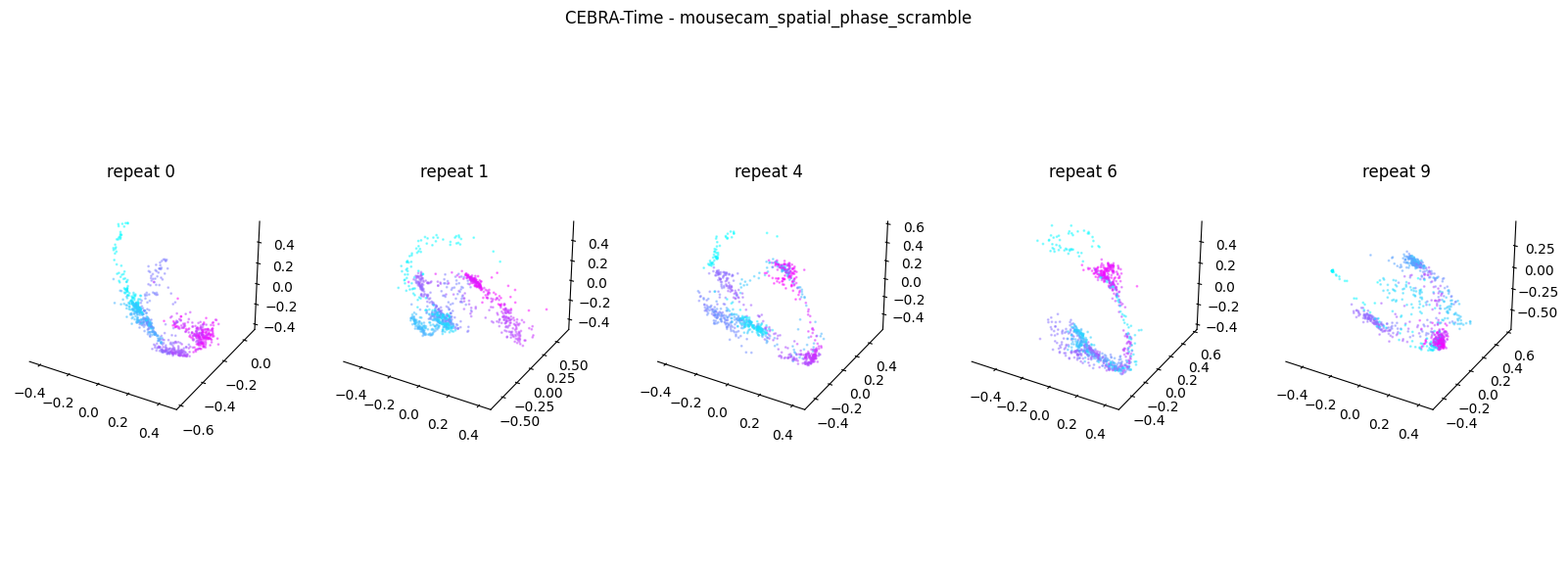
Averaged R2 test score 0.3419273335127083 for mousecam_spatial_phase_scramble

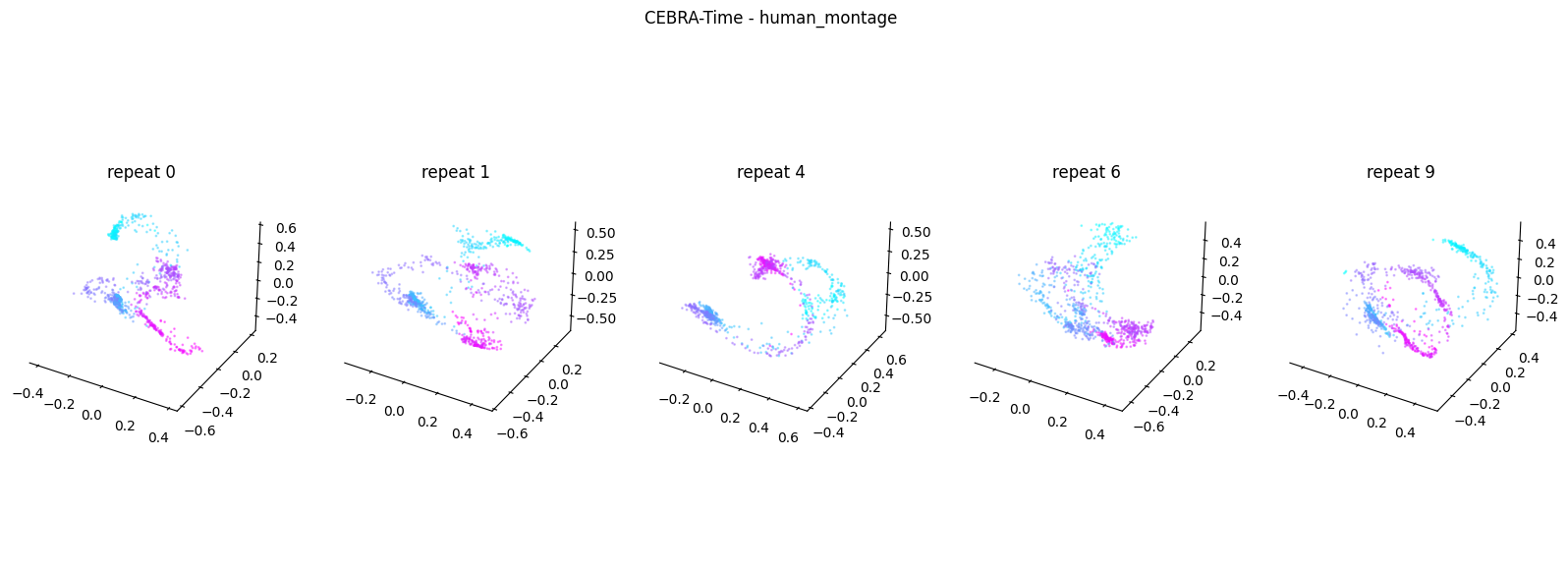
Averaged R2 test score 0.40574859994727774 for human_montage

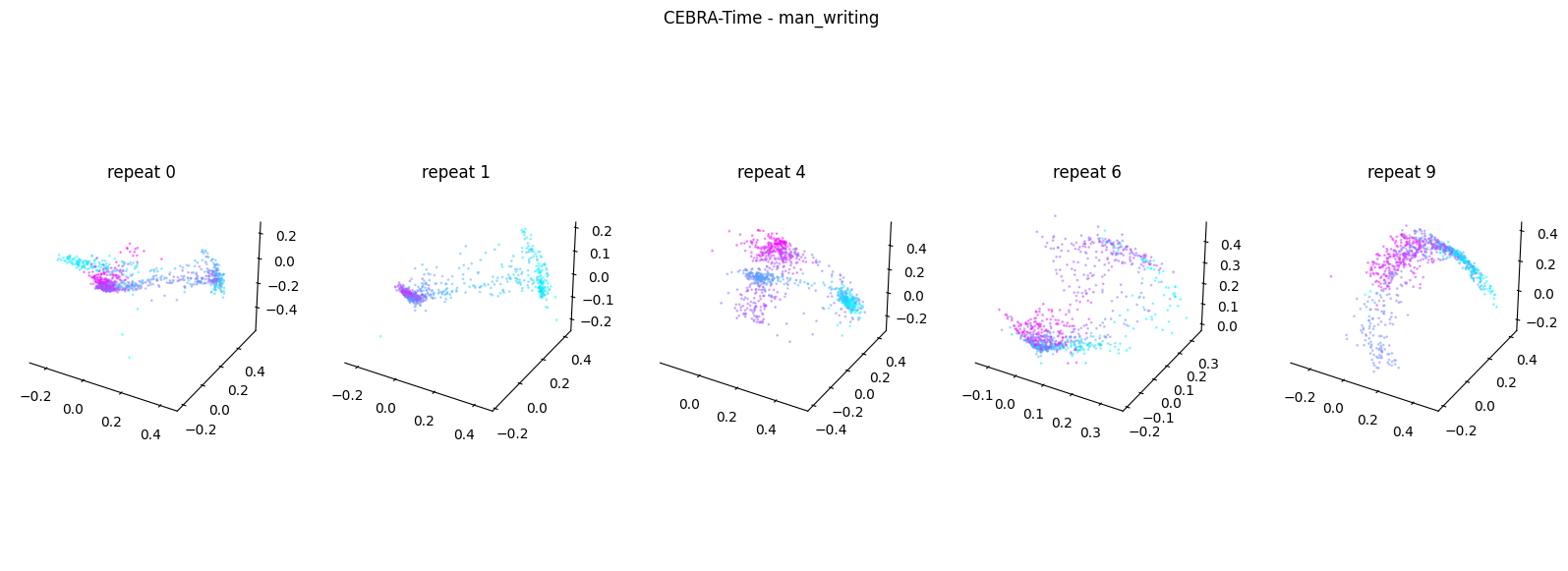
Averaged R2 test score 0.30765979595533427 for man_writing
Invalid stim

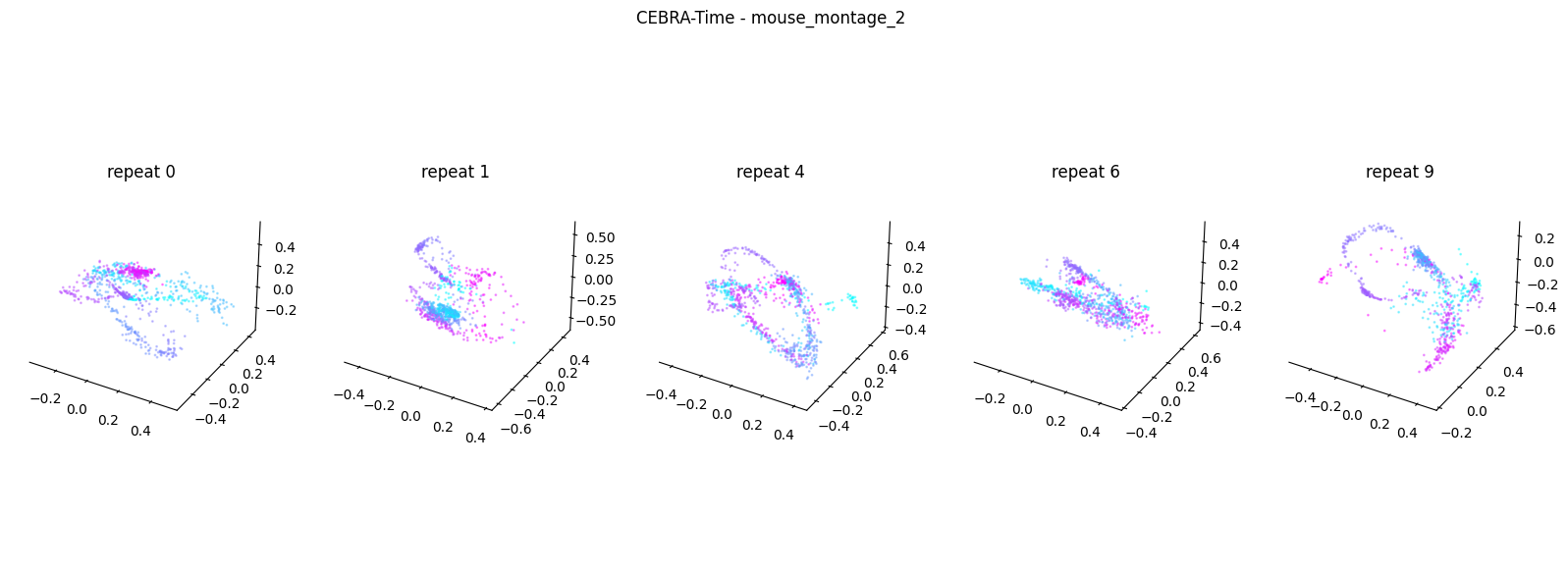
Averaged R2 test score -0.11536414366127998 for mouse_montage_2

In the code above we trained a KNN image decoder onto each movie. Our intent is to test which movie could better be encoded into the neuronal activity recorded during this session. Each movie contains stimuli that are more or less natural to a mouse. The hypothesis is that those more innate stimuli should yield higher decoding accuracy. The KNN decoder tries to predict which frame of the movie is displayed onto the screen solely from the neuronal activity. It does not tries to predict the movie name, just the frame number. For each movie, the performance of the decoder is measured using 10 folds. A fold is a single training/test split of the data. Here, we are splitting each dataset into training and test data 10 times and averaging the performance of all models.

# Extract keys and values from the dictionary
keys = list(store_scores.keys())
values = list(store_scores.values())

# Create a bar plot
plt.bar(keys, values)

# Adding labels and title
plt.xlabel("Movie name")
plt.xticks(rotation=-45, ha="left")

plt.ylabel("R^2 score from KNN cluster")

Text(0, 0.5, 'R^2 score from KNN cluster')

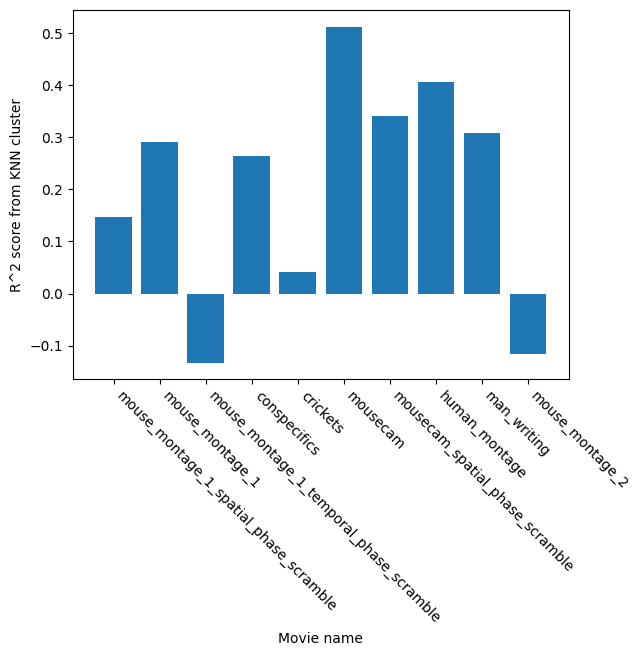
The above plot shows the ability of a clustering algorithm to predict the current frame solely from the embedding created by CEBRA. You can see that specific movie types are better predicted (r2_square value closer to 1). The original hypothesis of the study was to look into the meaningfulness of various movies. CEBRA can be used in this context to test how well each movie is represented by the neuronal activity.