Introduction to Generalized Linear Models using Pynapple and NeMoS#
Authors: Camila Maura, Edoardo Balzani & Guillaume Viejo
In this notebook, we will use Pynapple and NeMoS packages (supported by the Flatiron Institute), to model spiking neural data using Generalized Linear Models (GLM). We will explain what GLMs are and which are their components, then use Pynapple and NeMoS python packages to preprocess real data from the Primary Visual Cortex (VISp) of mice, and use a GLM model to predict spiking neural data as a function of passive visual stimuli. We will also show how, if you have recordings from a large population of neurons simultaneously, you can build connections between the neurons into the GLM in the form of coupling filters.
We will be analyzing data from the Visual Coding - Neuropixels dataset, published by the Allen Institute. This dataset uses extracellular electrophysiology probes to record spikes from multiple regions in the brain during passive visual stimulation. For simplicity, we will focus on the activity of neurons in the visual cortex (VISp) during passive exposure to full-field flashes of color either black (coded as “-1.0”) or white (coded as “1.0”) in a gray background.
We have three main goals in this notebook:
Introduce the key components of Generalized Linear Models (GLMs),
Demonstrate how to pre-process real experimental data recorded from mice using Pynapple, and
Use NeMoS to fit GLMs to that data and explore model-based insights.
By the end of this notebook, you should have a clearer understanding of the fundamental building blocks of GLMs, as well as how Pynapple and NeMoS can streamline the process of modeling and analyzing neural data, making it a much more accessible and efficient endeavor.
Background on GLMs#
A GLM is a regression model which trains a filter to predict a value (output) as it relates to some other variable (or input). In the neuroscience context, we can use a particular type of GLM to predict spikes: the linear-nonlinear-Poisson (LNP) model. This type of model receives one or more inputs and then sends them through a linear “filter” or transformation, passes said transformation through a nonlinearity to get the firing rate and uses that firing rate as the mean of a Poisson distribution to generate spikes. We will go through each of these steps one by one:
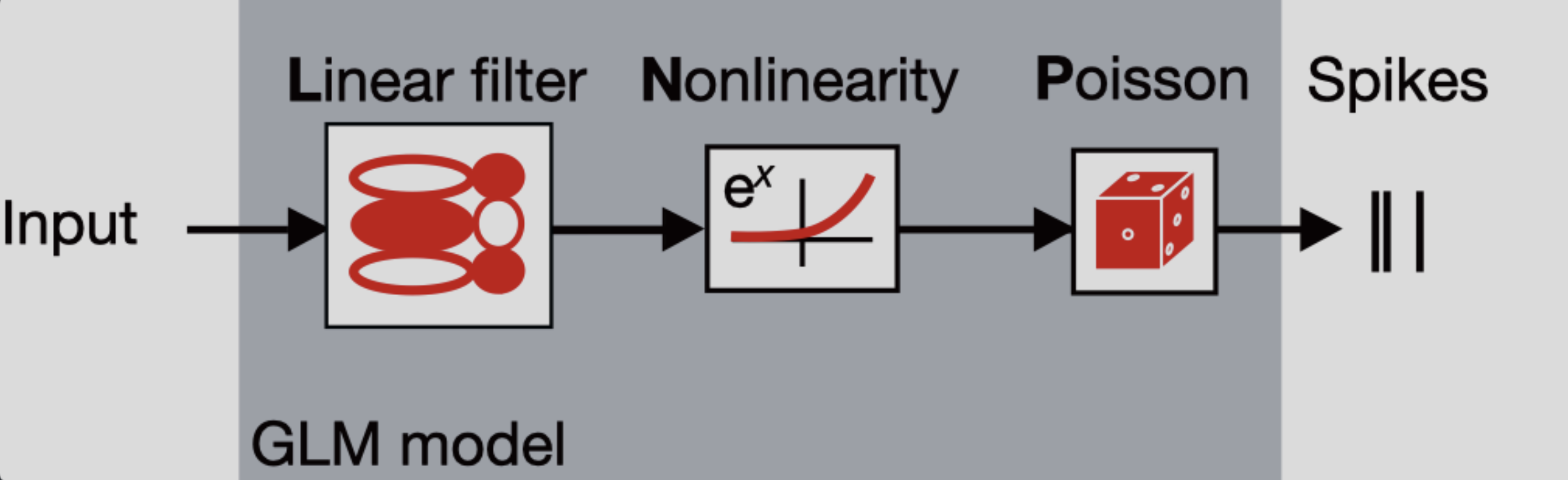
Sends the inputs through a linear “filter” or transformation
The inputs (also known as “predictors” or “filters”) are first passed through a linear transformation:
\[ \begin{aligned} L(X) = WX + c \end{aligned} \]Where \(X\) is the input (in matrix form), \(W\) is a matrix and \(c\) is a vector (intercept).
\(L\) scales (makes bigger or smaller) or shifts (up or down) the input. When there is zero input, this is equivalent to changing the baseline rate of the neuron, which is how the intercept should be interpreted. So far, this is the same treatment of an ordinary linear regression.
Passes the transformation through a nonlinearity to get the firing rate.
The aim of a LNP model is to predict the firing rate of a neuron and use it to generate spikes, but if we were only to keep \(L(X)\) as it is, we would quickly notice that we could obtain negative values for firing rates, which makes no sense! This is what the nonlinearity part of the model handles: by passing the linear transformation through an exponential function, it is assured that the resulting firing rate will always be non-negative.
As such, the firing rate in a LNP model is defined:
\[ \begin{aligned} \lambda = exp(L(X)) \end{aligned} \]where \(\lambda\) is a vector containing the firing rates corresponding to each timepoint.
A note on nonlinearity
In NeMoS, the nonlinearity is kept fixed. We default to the exponential, but a small number of other choices, such as soft-plus, are allowed. The allowed choices guarantee both the non-negativity constraint described above, as well as convexity, i.e. a single optimal solution. In principle, one could choose a more complex nonlinearity, but convexity is not guaranteed in general.
What is the difference between a “link function” and the “nonlinearity”?
The link function states the relationship between the linear predictor and the mean of the distribution function. If \(g\) is a link function, \(L(⋅)\) is the linear predictor and \(\lambda\) the mean of the distribution function:
the “nonlinearity” is the name for the inverse of the link function \(g^{-1}(⋅)\).
Uses the firing rate as the mean of a Poisson distribution to generate spikes
In this type of GLM, each spike train is modeled as a sample from a Poisson distribution whose mean is the firing rate — that is, the output of the linear-nonlinear components of the model.
Spiking is a stochastic process. This means that a given firing rate can lead to many different possible spike trains. Since the model could generate an infinite number of spike train realizations, how do we evaluate how well it explains the single observed spike train? We do this by computing the log-likelihood: it quantifies how likely it is to observe the actual spike train given the predicted firing rate. If \( y(t) \) is the observed spike count and \( \lambda(t) \) is the predicted firing rate at time \( t \), then the log-likelihood at time \( t \):
\[ \log P(y(t) \mid \lambda(t)) = y(t)\log\lambda(t) - \lambda(t) -\log(y(t)!) \]However, the term \( -\log(y(t)!) \) does not depend on \( \lambda \), and therefore is constant with respect to the model. As a result, it is usually dropped during optimization, leaving us with the simplified log-likelihood:
\[ \log P(y(t) \mid \lambda(t)) = y(t) \log \lambda(t) - \lambda(t) \]This forms the loss function for LNPs. In practice, we aim to maximize this log-likelihood, which is equivalent to minimizing the negative log-likelihood — that is, finding the firing rate \(\lambda(t)\) that makes the observed spike train as likely as possible under the model.
Why using GLMs?
Why not just use linear regression? Because neural data breaks its key assumptions. Linear regression expects normally distributed data with constant variance, but spike counts are non-Gaussian. Even more problematic, neural variability isn’t constant: neurons that fire more frequently also tend to be more variable. This violates the homoscedasticity assumption that’s fundamental to linear regression, making GLMs a much more suitable framework for modeling neural activity.
GLMs are as easy to fit as linear regression! The objective function (negative log-likelihood) of GLMs with canonical link functions (such as log link which we are using here) is convex, which means there is one local minimum and no local maxima, ensuring convergence to the right answer.
More resources on GLMs
If you would like to learn more about GLMs, you can refer to:
NeMoS GLM tutorial: for a bit more detailed explanation of all the components of a GLM within the NeMoS framework, as well as some nice visualizations of all the steps of the input transformation!
Introduction to GLM - CCN software workshop by the Flatiron Institute: for a step by step example of using GLMs to fit the activity of a single neuron in VISp under current injection.
Neuromatch Academy GLM tutorial: for a bit more detailed explanation of the components of a GLM, slides and some coding exercises to ensure comprehension.
Jonathan Pillow’s COSYNE tutorial: for a longer tutorial of all of the components of a GLM, as well as different types of GLM besides LNP
Environment setup and library imports#
# Install requirements for the databook
try:
from databook_utils.dandi_utils import dandi_download_open
except:
!git clone https://github.com/AllenInstitute/openscope_databook.git
%cd openscope_databook
%pip install -e .
# Import libraries
import seaborn as sns
from scipy.stats import zscore
import numpy as np
import matplotlib.pyplot as plt
import pynapple as nap
import nemos as nmo
Show code cell source
# Imports for ease of visualization
import warnings
import matplotlib as mpl
warnings.filterwarnings("ignore")
from matplotlib.ticker import MaxNLocator
from scipy.stats import gaussian_kde
from matplotlib.patches import Patch
# Parameters for plotting
custom_params = {"axes.spines.right": False, "axes.spines.top": False}
sns.set_theme(style="ticks", palette="colorblind", font_scale=1.5, rc=custom_params)
Download data#
# Dataset information
dandiset_id = "000021"
dandi_filepath = "sub-726298249/sub-726298249_ses-754829445.nwb"
download_loc = "."
# Download the data using NeMoS
io = nmo.fetch.download_dandi_data(dandiset_id, dandi_filepath)
Now that we have downloaded the data, it is very simple to open the dataset with Pynapple
data = nap.NWBFile(io.read(), lazy_loading=False)
nwb = data.nwb
print(data)
754829445
┍━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┯━━━━━━━━━━━━━┑
│ Keys │ Type │
┝━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┿━━━━━━━━━━━━━┥
│ units │ TsGroup │
│ static_gratings_presentations │ IntervalSet │
│ spontaneous_presentations │ IntervalSet │
│ natural_scenes_presentations │ IntervalSet │
│ natural_movie_three_presentations │ IntervalSet │
│ natural_movie_one_presentations │ IntervalSet │
│ gabors_presentations │ IntervalSet │
│ flashes_presentations │ IntervalSet │
│ drifting_gratings_presentations │ IntervalSet │
│ timestamps │ Tsd │
│ running_wheel_rotation │ Tsd │
│ running_speed_end_times │ Tsd │
│ running_speed │ Tsd │
│ raw_gaze_mapping/screen_coordinates_spherical │ TsdFrame │
│ raw_gaze_mapping/screen_coordinates │ TsdFrame │
│ raw_gaze_mapping/pupil_area │ Tsd │
│ raw_gaze_mapping/eye_area │ Tsd │
│ optogenetic_stimulation │ IntervalSet │
│ optotagging │ Tsd │
│ filtered_gaze_mapping/screen_coordinates_spherical │ TsdFrame │
│ filtered_gaze_mapping/screen_coordinates │ TsdFrame │
│ filtered_gaze_mapping/pupil_area │ Tsd │
│ filtered_gaze_mapping/eye_area │ Tsd │
│ running_wheel_supply_voltage │ Tsd │
│ running_wheel_signal_voltage │ Tsd │
│ raw_running_wheel_rotation │ Tsd │
┕━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┷━━━━━━━━━━━━━┙
Pynapple objects
When printing data, we can see four type of Pynapple objects:
TsGroup: Dictionary-like object to group objects with different timestampsIntervalSet: A class representing a (irregular) set of time intervals in elapsed time, with relative operationsTsd: 1-dimensional container for neurophysiological time series - provides standardized time representation, plus various functions for manipulating times series.TsdFrame: Column-based container for neurophysiological time series
To learn more, please refer to the Pynapple documentation
Extraction, preprocessing and stimuli revision#
Extracting spiking data#
We have a lot of information in data, but we are interested in the units.
(it might take a while the first time that you run this - it’s okay! the dataset is quite big)
units = data["units"]
# See the columns
print(f"columns : {units.metadata_columns}")
# See the dataset
print(units)
columns : ['rate', 'spread', 'velocity_below', 'silhouette_score', 'firing_rate', 'd_prime', 'nn_hit_rate', 'waveform_duration', 'amplitude', 'cluster_id', 'snr', 'local_index', 'peak_channel_id', 'PT_ratio', 'presence_ratio', 'max_drift', 'cumulative_drift', 'repolarization_slope', 'waveform_halfwidth', 'amplitude_cutoff', 'nn_miss_rate', 'quality', 'velocity_above', 'isolation_distance', 'l_ratio', 'recovery_slope', 'isi_violations']
Index rate spread velocity_below silhouette_score firing_rate d_prime nn_hit_rate waveform_duration amplitude cluster_id snr local_index peak_channel_id PT_ratio presence_ratio max_drift cumulative_drift repolarization_slope waveform_halfwidth amplitude_cutoff nn_miss_rate quality velocity_above isolation_distance l_ratio recovery_slope isi_violations
--------- -------- -------- ---------------- ------------------ ------------- --------- ------------- ------------------- ----------- ------------ ----- ------------- ----------------- ---------- ---------------- ----------- ------------------ ---------------------- -------------------- ------------------ -------------- --------- ---------------- -------------------- --------- ---------------- ----------------
951763702 2.38003 30 nan nan 2.38 4.77 0.98 1.52 78.67 0 2.09 0 850135036 1.38 0.98 23.02 425.42 0.1 0.73 0.5 0 good 0 63.68 0 -0 0.44
951763707 0.01147 80 nan 0.03 0.01 3.48 0 1.44 105.93 1 1.54 1 850135036 3.02 0.5 nan 0 0.05 2.18 0.5 0 noise -0.17 12.27 0.01 -0.39 0
951763711 3.1503 50 nan 0.17 3.15 6.08 1 1.04 189.17 2 1.44 2 850135038 2.35 0.99 14.29 328.21 0.12 0.91 0.03 0 good -0.27 63.87 0 -0.01 0.06
951763715 6.53 40 nan 0.12 6.53 5.04 0.99 1.28 191.85 3 1.43 3 850135038 2.05 0.99 27.45 369.58 0.18 0.63 0.01 0 good 0.62 47.54 0 -0.02 0.64
951763720 2.00296 40 0 0.2 2 6.45 0.99 0.27 316.89 4 4.28 4 850135044 0.63 0.99 39.21 214.71 1.37 0.15 0 0 good 0.34 59.93 0 -0.29 0.55
951763724 8.66233 60 -7.55 0.22 8.66 3.1 0.86 0.37 133.85 5 2.22 5 850135044 4.04 0.99 81.75 1245.94 0.37 0.23 0.2 0.01 noise 1.61 41.19 0.03 -0.04 0.55
951763729 11.134 30 -0.69 0.01 11.13 4.61 0.98 0.32 153.87 6 2.45 6 850135044 3.56 0.85 36.45 484.22 0.62 0.16 0.42 0 noise 0.69 91.43 0 -0.09 0.31
951763733 23.8915 60 -0.27 0.19 23.89 3.2 0.74 0.38 329.91 7 1.36 7 850135050 0.19 0.99 47.53 107.39 1.03 0.25 0 0.05 good 1.03 94.32 0.04 -0.23 0.11
951763737 1.01848 60 -0.27 0.12 1.02 3.61 0.32 0.51 251.6 8 3.22 8 850135050 0.93 0.63 36.8 86.37 0.31 0.29 0 0 noise 2.06 34.53 0.01 -0.14 8.63
951763741 11.8133 30 nan 0.15 11.81 1.99 0.25 1.21 110.32 9 0.43 9 850135050 0.4 0.93 88.68 774.76 0.01 1.29 0.37 0.05 noise 11.33 34.23 0.09 -0.02 0.06
951763745 13.4006 50 -9.47 0.02 13.4 1.8 0.24 1.15 95.07 10 0.33 10 850135050 0.43 0.99 98.87 894.51 0.01 1.33 0.35 0.05 noise 14.42 35.34 0.1 -0.02 0.06
951763749 18.2252 60 -8.45 0.01 18.23 1.85 0.35 1.54 96.28 11 0.32 11 850135050 0.52 0.99 128.7 1059.25 0.22 nan 0.28 0.06 noise 12.02 39.32 0.09 -0.01 0.17
951763753 18.9817 80 9.17 0.1 18.98 2.67 0.89 1.03 71.72 12 0.22 12 850135050 0.46 0.99 53.35 547.75 0.04 nan 0.25 0.01 noise -0.86 92.67 0.01 nan 0.11
951763758 13.2587 20 nan 0.04 13.26 4.44 0.95 1.11 147.66 13 0.68 13 850135050 0.49 0.54 29.68 255.01 0.02 nan 0.09 0 noise -25.41 62.62 0.01 nan 0.27
951763762 17.3762 40 8.93 0.01 17.38 1.74 0.32 2.01 105.62 14 0.33 14 850135050 0.54 0.91 121.76 921.06 0.1 nan 0.09 0.06 noise 11.68 37.33 0.1 -1.31 0.07
951763766 12.0932 60 -0.34 0.03 12.09 3.12 0.57 0.45 259.12 15 0.96 15 850135050 0.06 0.99 49.6 189.29 0.61 0.34 0 0.02 noise 1.37 42.2 0.05 -0.17 0.85
951763770 4.00705 120 -2.35 0.11 4.01 3.16 0.48 0.71 117.65 16 1.09 16 850135064 0.77 0.98 37.16 253.33 0.34 0.08 0.01 0.01 noise 0.1 37.27 0.03 -0.13 0.03
951763774 5.77131 120 -0.41 0.04 5.77 4.46 0.76 0.32 107.42 17 2.54 17 850135052 0.51 0.91 41.06 172.15 0.41 0.18 0.03 0.01 good -0.46 57.82 0.01 -0.09 0.04
951763778 1.15881 120 -0.48 -0.05 1.16 3.27 0.1 0.32 87.23 18 2.02 18 850135052 0.53 0.88 34.17 152.12 0.34 0.18 0.05 0 noise -1.77 26.81 0.03 -0.08 0.29
951763782 14.6012 50 -0.34 0.18 14.6 4.91 0.98 1.3 282.59 19 2.51 19 850135058 4.98 0.99 27.03 92.57 0.19 nan 0 0 good -0.69 63.43 0 -0.01 0
951763786 7.50032 50 -0.34 0.12 7.5 4.91 0.96 1.41 223.21 20 1.89 20 850135058 34.12 0.99 33.58 103.36 0.1 nan 0 0 good 0 58.26 0.01 -0.05 0.02
951763790 0.50676 70 -0.07 nan 0.51 4.22 0.33 0.48 204.91 21 1.88 21 850135058 0.95 0.66 7.77 24.52 0.67 0.18 0.06 0 good 0.27 36.67 0 -0.13 0.6
951763794 13.4125 40 -0.69 0.08 13.41 3.93 0.91 0.23 153.74 22 2.27 22 850135060 0.36 0.99 16.81 234.41 0.65 0.07 0.28 0 noise 0.34 59.03 0.01 -0.07 0.06
951763798 3.45524 90 -0.2 0.08 3.46 3.82 0.65 0.54 145.9 23 2.16 23 850135060 0.79 0.99 22.86 245.82 0.44 0.21 0.5 0 good -0.14 38.5 0.02 -0.05 0.16
951763802 14.2516 60 -0.34 0.17 14.25 3.97 0.77 0.62 229.05 24 3.05 24 850135062 0.43 0.99 41.46 115.68 0.63 0.25 0.06 0.01 good 0.41 55.09 0.02 -0.11 0.17
951763806 2.36639 70 -0.21 0.05 2.37 2.59 0.24 0.54 192.35 25 1.8 25 850135072 0.45 0.99 17.38 311.82 0.54 0.3 0.05 0 good 0 26.58 0.07 -0.09 0.19
951763808 10.4327 60 -0.27 0.02 10.43 2.9 0.53 0.36 300.37 26 1.06 26 850135050 0.08 0.99 49.98 153.06 0.97 0.27 0 0.02 good 1.03 37.43 0.05 -0.21 0.19
951763811 0.91494 50 -0.34 -0.01 0.91 4.15 0.26 0.54 223.67 27 2.99 27 850135062 0.37 0.94 10.11 49.54 0.73 0.22 0.02 0 noise 0.34 33.34 0.01 -0.08 0.74
951763815 8.95715 70 -0.41 -0 8.96 3.03 0.64 0.52 195.89 28 2.64 28 850135062 0.49 0.99 20.6 130.53 0.6 0.22 0.22 0.01 noise 0.48 49.55 0.02 -0.11 0.2
951763819 0.69669 70 -0.21 0.04 0.7 3.2 0.3 0.56 182.87 29 2.46 29 850135062 0.46 0.75 12.96 67.73 0.49 0.25 0.2 0 good 0.41 25.92 0.02 -0.08 0.96
951763823 15.7534 80 0.27 0.08 15.75 3.26 0.95 1.5 166.02 30 1.27 30 850135064 1.21 0.99 31.47 102.05 0.07 0.84 0.16 0 good 0.27 65.17 0.01 -0.02 0.03
951763828 20.426 50 0 0.17 20.43 7.35 1 0.36 387.75 31 4.76 31 850135066 0.9 0.99 47.82 104.69 1.47 0.19 0 0 good 0.34 129.98 0 -0.28 0
951763833 5.54128 50 -0.34 0.14 5.54 2.73 0.83 1.41 253.18 32 1.91 32 850135068 10.55 0.99 44.35 131.02 0.15 nan 0.5 0 good 0 49.27 0.01 -0.03 0.09
951763837 10.3832 40 -0.69 0.07 10.38 3.26 0.92 1.4 332.94 33 2.45 33 850135068 2.74 0.99 43.84 84.73 0.18 nan 0 0 good -0.34 50.35 0.02 -0.02 0.01
951763841 18.6182 70 0 0.09 18.62 2.77 0.91 1.04 253.41 34 1.85 34 850135068 7.92 0.99 47.61 117.71 0.15 nan 0.06 0.01 good -0.07 53.17 0.03 -0 0.03
951763845 12.7977 50 -1.37 0.07 12.8 4.31 0.96 1.26 207.72 35 1.64 35 850135068 11.52 0.99 37.5 94.2 0.13 nan 0.02 0.01 good 0 69.14 0 -0.01 0.03
951763849 11.4132 80 0.27 0.21 11.41 5.34 0.94 0.51 183.93 36 2.58 36 850135070 0.33 0.99 34 110.88 0.54 0.25 0 0 good 0.76 71.26 0 -0.09 0.04
951763854 2.52108 90 0.98 0.11 2.52 3.89 0.83 0.47 101.37 37 1.4 37 850135070 0.22 0.99 43.12 379.27 0.27 0.25 0.44 0 noise 1.17 48.78 0.01 -0.04 0.02
951763859 17.1477 60 -0.34 0.11 17.15 3.16 0.62 0.52 317.22 38 3.53 38 850135072 0.39 0.99 36.53 98.08 0.97 0.22 0.01 0.02 good 0.27 48.73 0.04 -0.18 0.06
951763863 0.59377 70 -0.48 -0.01 0.59 1.96 0.07 0.55 231.81 40 2.5 39 850135072 0.43 0.98 38.38 297.14 0.69 0.23 0.06 0 good 0.21 25.39 0.04 -0.12 0.22
951763867 0.03658 70 -0.21 nan 0.04 2.72 0 0.54 281.53 41 3.04 40 850135072 0.48 0.71 8.83 4.12 0.86 0.25 0.49 0 good 0.21 24.11 0.02 -0.19 0
951763874 0.01312 80 0 0.02 0.01 3.51 nan 0.52 227.62 42 2.19 41 850135072 0.44 0.49 nan 0 0.64 0.25 0.41 0 noise 0.49 27.82 0 -0.12 0
951763880 0.02273 170 -2.96 nan 0.02 5.65 0.17 0.33 14.44 43 0.17 42 850135478 2.71 0.47 12.28 37.9 0.05 0.73 0.4 0 noise 0.05 66.55 0 -0.02 0
951763887 5.85025 60 -0.69 0.12 5.85 3.98 0.97 1.46 175.92 44 2.17 43 850135076 1.2 0.99 13.59 157.41 0.08 0.76 0.5 0 good -0.14 70.07 0 -0.06 0.13
951763893 5.0215 100 -0.2 0.07 5.02 3.25 0.73 1.51 127.55 45 1.68 44 850135078 1.25 0.99 31.06 277.75 0.05 0.77 0.5 0 good 0.62 45.59 0.01 -0.03 0.11
951763901 6.27197 90 0.21 0.16 6.27 3.44 0.9 1.5 162.24 46 1.93 45 850135086 2.53 0.99 24.48 177.91 0.07 nan 0.04 0 good 2.34 60.28 0.01 nan 0.05
951763907 9.34383 80 0 0.11 9.34 3.11 0.97 0.54 211.34 47 3.05 46 850135082 0.61 0.99 27.14 116.85 0.62 0.23 0.04 0 good 0.48 67.6 0 -0.12 0.06
951763914 15.789 70 -0.21 0.14 15.79 6.13 0.99 0.55 244.26 48 1.99 47 850135084 0.6 0.99 32.78 87.27 0.66 0.19 0 0 good 0 113.55 0 -0.12 0
951763920 4.00488 110 0.04 0.1 4 2.75 0.77 0.59 158.2 49 1.42 48 850135084 0.56 0.99 16.87 275.2 0.36 0.33 0.5 0 good 0.16 50.12 0.01 -0.07 0.21
951763928 5.38287 60 0 0.36 5.38 5.01 0.96 0.51 684.2 50 4.44 49 850135084 0.81 0.99 49.61 98.27 1.97 0.26 0 0 good 0.41 61.92 0 -0.44 0
951763934 3.04221 60 0.34 0.15 3.04 2.97 0.88 0.96 223.44 51 1.14 50 850135084 0.34 0.99 43.2 212.11 0.58 0.3 0.5 0 good 0.21 46.77 0.01 -0.03 0.26
951763941 0.00816 50 -0.34 nan 0.01 4.4 nan 0.48 691.84 52 2.74 51 850135084 0.99 0.43 nan 0 1.83 0.34 0.5 0 noise 0.69 78.63 0 -0.7 0
951763947 1.57897 50 0 0.17 1.58 3.04 0.99 2.05 869.17 53 5.31 52 850135084 1.05 0.98 64.34 801.87 0.98 0.43 0.05 0 noise 0.34 67.51 0 nan 0.12
951763954 11.8275 60 -0.14 0.2 11.83 5.34 0.98 0.52 407.73 54 4.67 53 850135086 0.94 0.99 35.17 67.31 1.21 0.18 0 0 good 0.34 70.21 0 -0.17 0
951763961 8.62689 60 -0.14 0.06 8.63 2.82 0.95 1.5 234.27 55 2.82 54 850135086 1.65 0.99 28.47 109.43 0.12 1.47 0 0 good 0.69 70.55 0 -0.16 0.08
951763968 8.3856 70 0.76 0.19 8.39 4.54 0.99 1.29 245.66 56 3.3 55 850135088 2.21 0.99 34.87 106.33 0.13 0.96 0 0 good 0.69 79.37 0 -0.01 0.01
951763975 14.9898 70 0.48 0.13 14.99 5.46 0.98 1.09 232.1 57 2.92 56 850135090 1.02 0.99 35.15 74.72 0.13 0.67 0 0 good 0.62 78.92 0.01 0 0
951763982 12.1488 60 -0.69 0.18 12.15 3.6 0.79 0.56 145.48 59 2.5 57 850135092 0.43 0.99 19.53 80.96 0.39 0.32 0.13 0.02 good -1.03 80.68 0.01 -0.08 0.08
951763988 7.26286 60 -0.69 0.27 7.26 5.52 0.99 0.54 294.45 60 4.54 58 850135092 0.38 0.99 25.28 54.14 0.92 0.21 0 0 good 0.41 77.64 0 -0.16 0
951763994 5.46647 70 0.55 0.02 5.47 3 0.54 0.54 135.68 61 2.35 59 850135092 0.38 0.99 34.14 247.78 0.35 0.32 0.33 0.01 noise 1.03 44.64 0.02 -0.08 0.09
951764001 11.7287 80 0.14 0.17 11.73 4.51 0.97 1.11 166.75 62 2.57 60 850135094 1.25 0.99 17.56 115.6 0.09 0.77 0.23 0 good 0.62 84.56 0 0 0.11
951764008 0.15738 110 0.41 0.07 0.16 2.73 0 0.59 179.69 63 2.35 61 850135094 0.89 0.93 29.74 189.08 0.44 0.27 0.1 0 good 0.39 18.86 0.04 -0.09 0
951764014 2.82003 140 0.03 -0.01 2.82 2.77 0.25 0.98 42.76 64 0.38 62 850135122 3.25 0.99 81.96 945.36 0.03 nan 0.5 0.01 noise -0.01 30.14 0.03 nan 0.09
951764022 11.1967 70 -0.34 0.15 11.2 3.83 0.93 1.21 149.13 65 1.36 63 850135096 7.52 0.99 29.51 100.64 0.06 nan 0.08 0.01 good 0.34 67 0 -0.01 0.04
951764029 5.63883 80 -0.07 0.06 5.64 3.02 0.74 1.39 135.8 66 1.78 64 850135090 1.5 0.99 28.49 177 0.08 0.85 0.12 0 good 0.34 48.58 0.01 -0.01 0.09
951764035 11.5555 50 -0.34 0.15 11.56 3.75 0.94 0.59 147.52 67 1.94 65 850135100 0.95 0.99 33.98 112.86 0.36 0.27 0.12 0 good 1.37 64 0.01 -0.07 0.09
951764042 12.2763 50 -0.76 0.27 12.28 4.78 1 0.54 336.72 68 4.26 66 850135100 0.75 0.99 26.05 81.89 0.96 0.32 0 0 good 0 95.55 0 -0.18 0
951764049 3.296 40 -1.03 0.13 3.3 2.55 0.72 1.37 150.65 69 1.85 67 850135100 1.04 0.99 33.97 270.9 0.07 0.77 0.06 0 good 0 41.87 0.02 -0.03 0.23
951764055 7.28983 70 -0.27 0.22 7.29 4.45 0.87 1.22 250.02 70 2.46 68 850135102 1.58 0.99 27.69 85.71 0.14 0.84 0 0 good -0.69 62.86 0 -0.01 0.01
951764063 7.33901 50 -0.69 0.24 7.34 5.65 0.97 1.18 273.47 71 2.63 69 850135102 1.4 0.99 21.86 74.28 0.17 0.82 0 0 good 1.03 64.91 0 -0 0
951764070 10.6127 80 -1.44 0.13 10.61 3.09 0.97 1.39 157.74 72 1.59 70 850135102 2.91 0.99 25.1 122.97 0.08 1.07 0.16 0 good 0.21 76.71 0 -0.01 0.03
951764076 3.39117 80 -0.1 0.05 3.39 2.28 0.48 1.48 193.47 73 1.68 71 850135102 2.61 0.99 26.58 231.56 0.09 1.04 0.5 0.01 good -0.34 35.86 0.03 -0.1 0.14
951764083 10.1095 70 -0.34 0.22 10.11 5.39 0.98 1.57 221.12 74 2.27 72 850135102 1.94 0.99 30.58 103.97 0.13 1.41 0 0 good 0.62 76.5 0 -0.14 0
951764090 14.326 30 -0.69 0.14 14.33 6.02 1 0.55 362.63 75 4.38 73 850135104 0.63 0.99 29.14 58.24 0.99 0.27 0 0 good nan 90.99 0 -0.2 0
951764099 11.0116 60 -0.14 0.07 11.01 3.51 0.96 0.51 167.25 76 2.15 74 850135108 0.81 0.99 29.02 109.5 0.5 0.23 0.1 0 good 0.69 66.59 0 -0.1 0.02
951764106 12.9879 80 -0.69 0.11 12.99 2.44 0.95 0.58 225.94 77 2.86 75 850135108 0.58 0.99 24.5 86.23 0.54 0.29 0.04 0 good 0.27 64.34 0 -0.08 0.03
951764112 8.86983 50 -2.06 0.1 8.87 4.32 0.95 0.51 256.97 78 3.1 76 850135108 0.57 0.99 16.09 74.1 0.79 0.19 0 0 good 0.62 65.45 0 -0.14 0.04
951764118 4.8696 50 -0.69 0.14 4.87 2.12 0.89 0.47 297.7 79 3.39 77 850135112 0.73 0.97 32.92 408.72 1.02 0.16 0 0 good 0.69 43.51 0.02 -0.13 0.11
951764125 4.77381 70 -0.21 0.12 4.77 3.1 0.54 0.54 150.03 80 2.52 78 850135110 0.7 0.99 15.09 191.94 0.43 0.26 0.5 0.01 good -0.21 42.81 0.02 -0.08 0.25
951764132 11.0504 70 -0.76 0.1 11.05 3.17 0.92 0.52 157.43 81 2.73 79 850135110 0.7 0.99 32.49 98.35 0.46 0.21 0.01 0 good 0.21 58.85 0.01 -0.07 0.02
951764139 6.14549 80 0 0 6.15 3.69 0.74 0.51 171.94 82 2.81 80 850135110 0.69 0.99 15.5 169.7 0.5 0.25 0.12 0.01 good -0.48 56.27 0.01 -0.1 0.12
951764147 7.73138 70 -0.48 0.08 7.73 3.6 0.89 1.46 154.24 83 1.99 81 850135112 1.35 0.99 19.71 109.97 0.11 0.69 0.1 0 good 0.07 59.23 0.01 -0.01 0.07
951764155 7.7847 60 -1.03 0.18 7.78 6.5 0.99 0.56 392.87 84 4.66 82 850135112 0.66 0.99 30.35 68.68 1.19 0.23 0 0 good 0.48 80.58 0 -0.2 0
951764162 3.00635 90 -0.07 0.1 3.01 2.71 0.64 0.66 136.1 86 2.06 83 850135114 0.29 0.99 16.32 212.82 0.36 0.3 0.5 0 good 0.14 36.71 0.02 -0.06 0.19
951764169 0.58705 80 -0.69 0.13 0.59 3.69 0.8 1.44 141.25 87 1.77 84 850135112 1.27 0.99 25.87 412.24 0.07 0.8 0.26 0 good -0.62 45.93 0 -0.08 0.22
951764175 11.2825 50 0 0.31 11.28 9.6 1 0.51 477.19 88 5.8 85 850135120 0.59 0.99 29.87 110.84 1.62 0.19 0 0 good 0.34 160.48 0 -0.25 0
951764182 3.69808 70 -1.03 0.07 3.7 3.87 0.9 0.55 121.15 89 1.84 86 850135116 0.51 0.99 29.3 193.6 0.35 0.19 0.5 0 good 0.14 60.78 0 -0.04 0.39
951764190 8.31926 60 0 0.05 8.32 5.17 0.98 0.63 165.47 90 2.33 87 850135116 0.66 0.99 27.66 87.8 0.36 0.26 0 0 good 1.37 76.42 0 -0.08 0.01
951764196 2.44906 80 -0.55 0.1 2.45 2.61 0.94 0.54 173.42 91 1.83 88 850135120 0.69 0.99 19.9 308.01 0.56 0.16 0.45 0 good 0.89 63.26 0 -0.07 0.3
951764203 14.0843 50 -0.34 0.39 14.08 10.14 1 0.54 597.12 92 5.17 89 850135122 0.74 0.99 30.94 73.26 1.8 0.21 0 0 good 0 179.49 0 -0.31 0
951764210 5.32293 120 -1.23 0.08 5.32 2.41 0.52 1.3 84.48 94 0.88 90 850135124 1.36 0.99 43.03 341.19 0.04 1.21 0.48 0.02 good 3.35 45.81 0.03 nan 0.21
951764216 19.1162 70 -0.27 0.14 19.12 4.23 0.99 0.49 215.29 95 2.71 91 850135124 0.64 0.99 24.36 85.83 0.69 0.26 0 0.01 good 0.76 105 0 -0.12 0.01
951764224 3.83655 80 -0.69 0.08 3.84 2.57 0.57 0.66 116.01 96 1.18 92 850135124 0.89 0.99 30.09 354.25 0.24 0.29 0.48 0.01 good 0.37 39.91 0.04 -0.08 0.31
951764232 5.33502 80 -1.03 0.17 5.34 5.12 0.94 1.22 189.07 97 1.89 93 850135118 2.04 0.99 29.81 222.13 0.09 1.06 0.04 0 good -0.24 69.38 0 -0.01 0.31
951764239 3.92841 60 -0.34 0.14 3.93 3.6 0.94 0.45 164.54 98 1.46 94 850135126 0.01 0.98 9.06 146.4 0.55 0.26 0.13 0 good 0.55 74.03 0 -0.07 0.12
951764246 5.55037 60 -0.69 0.32 5.55 8.69 1 0.45 443.82 99 4.3 95 850135126 0.31 0.99 21.27 56.42 1.33 0.23 0 0 good 0.41 129.84 0 -0.24 0
951764250 6.62693 50 -0.69 0.31 6.63 6.57 0.99 0.49 418.96 100 4.28 96 850135128 0.71 0.99 27.29 75 1.4 0.15 0 0 good 0.34 85.05 0 -0.19 0
951764254 0.49198 140 -0.26 0.17 0.49 2.12 0.19 0.62 111.44 102 1.18 97 850135130 0.06 0.8 20.49 154.47 0.29 0.41 0.5 0 noise -0.32 28.39 0.04 -0.03 1.76
951764259 7.92751 60 0.27 0.16 7.93 5 0.96 0.52 164.39 103 2.65 98 850135132 0.3 0.99 15.32 97.82 0.51 0.25 0.03 0 good -0.34 73.17 0 -0.07 0.26
951764263 5.8641 170 -1.13 0.02 5.86 2.31 0.58 1.32 45.24 104 0.34 99 850135128 1.58 0.86 39.06 291.98 0.02 nan 0.38 0.01 good 0.47 47.93 0.02 nan 1.1
951764268 4.06389 60 -0.62 0.32 4.06 4.83 0.99 0.47 338.2 105 3.64 100 850135134 0.95 0.99 31.05 89.91 1.07 0.16 0 0 good 0 87.29 0 -0.17 0
951764272 14.842 70 -0.69 0.08 14.84 3.9 0.96 1.57 239.46 106 2.53 101 850135134 1.63 0.99 50.71 584.15 0.14 0.82 0 0 good -0.55 63.47 0.02 nan 0.03
951764276 1.14734 100 -0.2 0.02 1.15 2.61 0.65 1.35 154.86 107 0.94 102 850135134 3.86 0.98 45.41 135.73 0.04 nan 0.49 0 noise -0.07 42.43 0.01 -0.02 0.82
951764279 10.7474 60 0.34 0.13 10.75 4.73 0.97 0.55 227.53 108 3.17 103 850135138 0.68 0.99 24.86 77.78 0.67 0.21 0.01 0 good 0.41 73.46 0 -0.11 0.02
951764284 4.16102 90 -0.69 0.13 4.16 2.12 0.55 0.55 144.3 109 1.75 104 850135138 0.86 0.99 50.53 235.54 0.36 0.29 0.5 0.01 good -0.2 36.42 0.05 -0.07 0.39
951764287 4.80088 70 -0.62 0.14 4.8 3.13 0.68 1.09 150.94 110 1.3 105 850135140 23.67 0.99 24 151.53 0.11 nan 0.21 0 good 0 42.61 0.02 -0.01 0.23
951764293 16.162 80 -1.03 0.07 16.16 5.22 0.98 1.35 208.23 111 1.89 106 850135140 2.98 0.99 24.74 76.61 0.11 nan 0 0 good -0.27 85.28 0 -0 0.03
951764299 9.321 80 0.21 0.07 9.32 3.38 0.95 1.5 150.14 112 1.39 107 850135140 6.74 0.99 16.04 114.15 0.08 nan 0.31 0.01 good 0.62 69.55 0 -0.09 0.07
951764305 12.0763 60 -1.44 0.13 12.08 3 0.96 1.46 152.91 113 1.67 108 850135142 1.84 0.99 32.6 102.77 0.09 1.13 0.03 0 good 1.03 72.79 0 nan 0.07
951764312 13.7481 50 -0.69 0.13 13.75 3.36 0.84 1.47 233.83 115 2.63 109 850135142 1.02 0.99 34.64 85.71 0.09 0.78 0 0.01 good 0.21 50.64 0.03 -0.01 0.02
951764319 2.25282 90 -1.1 0.05 2.25 2.45 0.35 1.51 267.34 116 2.65 110 850135142 1.07 0.99 17.01 223.55 0.12 0.76 0.03 0 good -0.29 26.04 0.12 nan 0.33
951764325 14.3434 60 -0.41 0.13 14.34 4.66 0.97 1.33 232.55 117 1.96 111 850135146 3.02 0.99 28.98 84.5 0.15 1.25 0.01 0 good 0.34 71.41 0 -0.01 0.03
951764332 6.43751 70 -0.96 0.26 6.44 4.59 0.97 1.4 313.16 118 3.19 112 850135148 1.68 0.99 38.3 84.53 0.16 1.22 0 0 good 0 57.14 0 0 0.02
951764338 6.4588 80 -0.89 0.09 6.46 3.03 0.82 1.22 137.86 119 1.52 113 850135148 9.42 0.99 32.3 160.44 0.06 nan 0.5 0.01 good -0.41 54.14 0.01 -0.01 0.35
951764344 12.0088 70 -0.41 0.14 12.01 3.45 0.53 1.26 170.19 120 2.03 114 850135150 8.49 0.99 17.23 94.34 0.09 nan 0.09 0.03 good 0.14 47.58 0.03 -0 0.16
951764350 10.6634 80 -1.25 0.06 10.66 2.7 0.6 1.54 102.21 121 1.18 115 850135150 5.14 0.99 28.25 208.47 0.08 nan 0.3 0.02 good 0 42.69 0.03 nan 0.13
951764357 11.6866 70 -0.21 0.04 11.69 2.57 0.47 1.14 149.83 122 1.75 116 850135150 9.84 0.99 29.84 124.9 0.09 nan 0.29 0.02 good 0.34 40.96 0.04 -0 0.32
951764364 6.12068 80 -0.48 0.04 6.12 2.44 0.48 1.41 185.55 123 2.4 117 850135150 5.61 0.99 11.09 141.89 0.1 nan 0.21 0.01 good 0 33.84 0.05 -0.02 0.41
951764370 14.4044 60 -0.62 0.15 14.4 5.44 0.98 0.48 256.02 124 3.28 118 850135152 0.43 0.99 26.14 74.55 0.83 0.22 0 0 good 0 75.75 0 -0.13 0.02
951764374 4.53159 70 -0.41 0.05 4.53 2.88 0.74 0.58 129.24 125 1.54 119 850135152 0.42 0.99 23.47 155.69 0.38 0.22 0.5 0.01 good 0.34 48.01 0.01 -0.05 0.26
951764379 4.49532 50 -1.72 0.18 4.5 3.39 0.35 0.62 192.49 126 2.63 120 850135156 0.69 0.99 30.38 187.65 0.45 0.25 0.06 0.01 good 0.69 35.32 0.03 -0.09 0.11
951764385 8.29497 50 -2.06 0.02 8.29 4.39 0.64 0.67 183.15 127 2.55 121 850135156 0.68 0.99 26.3 113.55 0.43 0.23 0.01 0.02 good 0.69 56.15 0.01 -0.1 0.06
951764390 3.70893 90 -1.14 0.06 3.71 4.08 0.27 0.65 216.27 128 2.86 122 850135156 0.68 0.99 23.48 132.5 0.44 0.29 0.02 0 good 0.41 32.07 0.03 -0.06 0.12
951764396 5.75643 70 -0.34 0.08 5.76 3.36 0.82 0.58 161.44 129 2.42 123 850135156 0.74 0.99 22.4 168.78 0.4 0.27 0.5 0 good 0.34 57.67 0.01 -0.08 0.06
951764403 1.74472 170 0.78 0.04 1.74 3.14 0.75 1.11 39.29 130 0.56 124 850135156 1.86 0.73 43.2 300.61 0 nan 0.5 0 noise 1.16 47.05 0 -0 0.19
951764409 2.02507 70 -0.69 0.06 2.03 2.57 0.3 0.55 186.02 131 2.53 125 850135156 0.52 0.99 14.65 222.21 0.57 0.18 0.46 0 noise 0 33.19 0.02 -0.07 0.26
951764415 22.8442 60 -0.34 0.22 22.84 5.03 0.98 1.44 394.15 132 3.57 126 850135158 1.3 0.99 24.85 55.77 0.23 0.77 0 0 good 0.14 73.29 0.01 -0.02 0.01
951764421 11.9241 80 0 0.11 11.92 2.85 0.95 1.35 190.96 133 2.13 127 850135158 5.75 0.99 22.18 107.95 0.1 nan 0.1 0 good 0.48 67.95 0 -0 0.04
951764426 2.71742 60 0 0.04 2.72 2.13 0.34 1.21 216.72 134 1.98 128 850135158 3 0.95 18.87 112.71 0.13 1.59 0.23 0.01 noise 0.41 33.84 0.02 -0.01 0.25
951764432 14.0462 60 0 0.04 14.05 2.78 0.81 1.3 257.67 135 2.43 129 850135158 2.32 0.99 15.88 84.43 0.17 1.37 0.05 0.01 good 0.21 61.72 0.01 -0.02 0.17
951764438 22.7161 50 0 0.14 22.72 4.93 0.96 0.38 269.76 136 3.31 130 850135160 0.47 0.99 23.52 68.4 1 0.16 0 0 good 0 89.63 0 -0.18 0.02
951764443 14.2488 60 -0.14 0.09 14.25 3.93 0.95 1.61 201.23 137 2.01 131 850135162 1.09 0.99 21.46 123.04 0.12 0.84 0.01 0 good 0.34 65 0.01 nan 0.06
951764447 3.7575 40 -0.34 0.34 3.76 5.66 0.98 1.19 411.01 139 4.19 132 850135164 2.63 0.99 20.21 58.61 0.26 0.78 0 0 good 0 79.97 0 -0 0
951764454 8.93462 70 -0.34 0.17 8.93 2.77 0.87 1.52 182.8 140 1.78 133 850135164 30.45 0.99 29.2 157.45 0.11 nan 0.11 0 good 0.34 50.85 0.01 -0.04 0.11
951764460 20.9761 50 0 0.18 20.98 4.19 0.94 0.48 301.04 141 3.29 134 850135166 0.31 0.99 30.39 71.88 0.96 0.25 0 0.01 good 0 77.75 0.01 -0.17 0.02
951764466 3.91136 70 0 0.06 3.91 2.22 0.4 0.49 210.82 143 2.19 135 850135166 0.24 0.99 14.37 187.8 0.68 0.27 0.5 0 good 0 34.29 0.03 -0.11 0.3
951764472 15.2495 60 0 0.11 15.25 3.7 0.95 0.47 224.32 144 2.61 136 850135168 0.72 0.99 24.11 91.85 0.72 0.21 0.02 0 good 0.34 90.81 0 -0.11 0.01
951764478 17.1805 50 -0.34 0.21 17.18 5.34 0.98 0.51 364.67 146 3.48 137 850135170 0.4 0.99 24.11 52.17 1.1 0.25 0 0 good 0.34 96.03 0 -0.18 0
951764484 5.14984 60 -0.76 0.12 5.15 3.24 0.85 0.56 164.88 147 1.8 138 850135172 0.28 0.99 35.82 201.39 0.37 0.32 0.5 0 good 0.69 46.7 0.01 -0.08 0.07
951764490 3.234 50 -0.69 0.22 3.23 4.18 0.86 0.45 388.57 148 3.8 139 850135172 0.46 0.99 25.66 90.47 1.3 0.22 0 0 good 0.69 39.48 0.01 -0.3 0.14
951764496 10.2851 60 0.62 0.06 10.29 3.91 0.88 0.49 183.02 149 2.15 140 850135172 0.28 0.99 35.99 104.34 0.54 0.32 0 0.01 good 1.03 63.62 0.01 -0.13 0.04
951764503 20.7697 60 -0.34 0.18 20.77 4.33 0.98 0.45 319.22 150 2.99 141 850135170 0.45 0.99 31.78 87.22 1.02 0.25 0 0 good 0.27 75.24 0 -0.17 0.02
951764508 3.69643 60 0 0.07 3.7 3.15 0.9 1.61 236.92 151 1.62 142 850135174 16.57 0.99 5.65 179.31 0.14 nan 0.5 0 good 0.69 49.97 0 nan 0.39
951764514 12.4374 60 0 0.18 12.44 4.06 0.95 0.54 288.36 152 2.58 143 850135170 0.37 0.99 28.02 112.88 0.78 0.26 0 0 good 0.55 63.79 0 -0.12 0.04
951764520 10.2671 60 0.34 0.13 10.27 3.35 0.95 0.87 173.07 153 2.12 144 850135176 1.35 0.99 13.97 124.88 0.12 0.67 0.11 0 good 1.37 70.56 0 -0 0.08
951764525 5.52423 50 -2.06 0.09 5.52 3.89 0.94 1.03 141.4 154 0.96 145 850135174 1.98 0.99 14.46 162.9 0.1 nan 0.12 0 good 2.06 72.36 0 -0.02 0.03
951764531 12.6207 20 0 0.38 12.62 7.11 0.99 0.54 605.84 155 5.77 146 850135180 0.52 0.99 10.36 28.82 1.88 0.21 0 0 noise nan 75.96 0 -0.34 0
951764537 11.6708 110 0.59 0.09 11.67 nan nan 0.47 59.14 156 0.46 147 850135180 0.47 0.99 53.49 326.22 0.13 0.26 0.24 0 noise 1.02 nan nan -0.04 0.25
951764543 3.67886 50 0.21 0.12 3.68 2.35 0.46 0.48 234.65 157 2.38 148 850135180 0.63 0.99 24.76 279.28 0.7 0.29 0.5 0.01 good 0.69 37.28 0.02 -0.13 0.24
951764550 4.92685 40 0.14 0.03 4.93 2.52 0.56 0.47 224.94 158 2.28 149 850135180 0.58 0.99 33.29 176.93 0.67 0.27 0.5 0.01 good nan 47.92 0.01 -0.14 0.16
951764557 9.14284 70 -6.59 0.07 9.14 2.31 0.79 0.52 77.68 159 0.86 150 850135180 0.5 0.99 18.49 229.16 0.23 0.29 0.28 0.01 good -0.69 66.24 0.01 -0.06 0.29
951764563 10.5269 30 0.34 0.29 10.53 5.38 0.88 0.41 484.4 160 3.13 151 850135182 0.99 0.99 12.41 42.55 1.66 0.15 0 0 good nan 54.51 0.01 -0.34 0.01
951764570 11.5479 60 -0.21 0.1 11.55 4.41 0.98 1.52 239.75 161 1.5 152 850135182 1.97 0.99 35.03 106.12 0.14 0.89 0.01 0 good 0.34 71.52 0 -0.09 0.03
951764576 6.09557 160 2.4 0.07 6.1 nan nan 1.11 39.32 162 0.1 153 850135182 1.28 0.99 43.9 810.05 0.03 nan 0.49 0 noise 1.12 nan nan -0.01 0.24
951764582 3.42961 170 0.47 0.02 3.43 nan nan 0.88 39.19 163 0.25 154 850135182 2.26 0.99 84.01 917.58 0.06 1.46 0.5 0 noise -0.4 nan nan 0 0.08
951764589 5.32965 160 0.79 0.02 5.33 nan nan 1.18 48.64 164 0.16 155 850135182 2.38 0.99 48.75 1006.26 0.01 1.4 0.41 0 noise 0.84 nan nan -0.02 0.09
951764595 6.93115 160 -0.39 0.01 6.93 3.32 0.88 1.09 49.7 165 0.24 156 850135182 10.4 0.97 72.91 674.81 0 1.65 0.35 0.01 noise 0.67 70 0 nan 0.13
951764601 3.70697 130 1.27 -0 3.71 nan nan 1.25 55.59 166 0.29 157 850135182 7.79 0.98 82.49 1050.73 0.05 1.19 0.5 0 noise -2.79 nan nan -0.03 0.1
951764608 18.6999 60 0.27 0.15 18.7 3.01 0.93 1.04 230.74 167 1.47 158 850135182 1.83 0.99 26.88 91.9 0.13 1.22 0.01 0.01 good 0 66.6 0.01 -0.01 0.03
951764614 15.2261 50 -1.37 0.09 15.23 4.43 0.96 0.48 197.19 168 2.92 159 850135186 0.87 0.99 14.87 82.23 0.61 0.22 0.01 0 good 0 64.97 0.01 -0.14 0.02
951764618 1.6015 70 0 0.14 1.6 2.98 0.44 0.52 207.03 169 2.77 160 850135186 0.84 0.99 16.35 273 0.61 0.22 0.04 0 good 0.21 26.8 0.06 -0.11 0.27
951764622 13.3591 40 -0.69 0.07 13.36 3.36 0.88 1.51 241.36 170 1.53 161 850135182 2 0.99 18.59 94.42 0.18 0.73 0.01 0.01 good 0.34 52.06 0.02 -0.06 0.05
951764624 13.0301 50 -0.34 0.15 13.03 2.96 0.93 0.44 173.5 171 2.62 162 850135188 0.28 0.99 17.01 101.88 0.59 0.29 0.5 0 good 0 71.24 0.01 -0.12 0.25
951764626 11.5823 20 nan 0.07 11.58 4.43 0.95 0.44 240.42 172 3.42 163 850135188 0.36 0.99 27.46 72.69 0.81 0.25 0 0 good 1.37 59.18 0.01 -0.16 0.01
951764630 7.20716 40 0 0.12 7.21 4.51 0.93 0.45 197.09 173 2.55 164 850135190 0 0.99 23.69 166.24 0.67 0.29 0.2 0 good 0.34 54.75 0.01 -0.12 0.23
951764635 5.02522 50 0.34 0.27 5.03 7.53 1 0.49 347.15 174 5.55 165 850135192 0.42 0.99 25.15 55.36 1.11 0.19 0 0 good 0.69 92.62 0 -0.19 0
951764639 10.251 60 -7.07 0.09 10.25 2.48 0.49 0.48 112.36 175 1.44 166 850135196 0.42 0.99 67.16 281.5 0.33 0.3 0.14 0.02 good 0 39.14 0.05 -0.07 0.08
951764644 13.5192 50 0.14 0.01 13.52 3.09 0.67 0.48 172.02 176 2.4 167 850135196 0.47 0.99 31.34 112.85 0.5 0.29 0.15 0.03 good -0.69 57.46 0.02 -0.1 0.03
951764648 8.21975 40 0 0.15 8.22 5.73 0.98 0.4 329.23 177 4.27 168 850135196 0.48 0.99 19.13 71.28 1.19 0.18 0 0 good -0.69 69.88 0 -0.23 0.01
951764652 6.23229 60 -1.99 0.08 6.23 4.13 0.85 0.47 163.54 178 2.11 169 850135196 0.41 0.99 15.8 227.39 0.54 0.23 0.5 0.01 good 0 60.61 0.01 -0.11 0.12
951764656 5.28139 50 -1.17 0.04 5.28 2.15 0.34 0.54 85.26 179 1 170 850135196 0.49 0.99 24.37 331.74 0.21 0.38 0.5 0.01 noise 0.69 34.98 0.05 -0.06 0.11
951764663 0.00093 160 2.36 nan 0 3.85 nan 0.22 221.89 180 2.75 171 850135196 1.11 0.09 nan 0 0.96 0.14 0.36 0 noise 2.66 4.48336e+12 nan -0.29 0
951764669 3.9993 70 -0.14 0.19 4 4.38 0.52 1.68 170.8 181 1.45 172 850135198 3.39 0.99 14.31 147.96 0.1 nan 0.13 0.01 good 0.21 45.22 0.02 nan 1.4
951764675 4.10233 70 -0.21 0.02 4.1 4.21 0.57 0.95 156.97 182 1.16 173 850135198 3.37 0.99 15.12 155.57 0.12 nan 0.2 0.01 good 0.21 48.58 0.01 -0.01 1.6
951764681 1.56647 70 -0.27 0.18 1.57 2.84 0.8 1.29 167.88 183 2.09 174 850135200 1.27 0.99 35.17 286.59 0.11 0.66 0.14 0 good 0.69 43.89 0.01 -0.01 0.32
951764688 1.50726 70 -0.34 0.13 1.51 4.1 0.72 1.32 185.03 184 1.67 175 850135198 3.31 0.99 16.1 176.19 0.12 nan 0.02 0 good 0.14 35.9 0.03 -0.01 1.14
951764694 2.66358 90 -0.07 0.05 2.66 2.63 0.75 0.44 110.23 185 2.32 176 850135202 0.44 0.99 19.57 265.47 0.39 0.22 0.5 0 good -0.14 41.73 0.02 -0.07 0.57
951764700 4.42691 70 -1.99 0.14 4.43 6.33 0.99 0.49 102.15 186 1.76 177 850135204 0.13 0.99 19.77 168.42 0.29 0.37 0.35 0 good -0.55 80.47 0 -0.05 0.12
951764706 10.0951 70 -0.21 0.09 10.1 4.84 0.95 0.43 159.53 187 3.04 178 850135206 0.26 0.99 10.66 84.31 0.6 0.18 0.01 0.01 good 0.21 60.83 0.01 -0.09 0.08
951764714 3.74241 80 0.06 0.07 3.74 4.04 0.86 0.49 115.39 188 2.22 179 850135206 0.33 0.99 12.39 269.85 0.38 0.26 0.5 0 good 0 54.61 0 -0.07 0.22
951764718 9.8384 60 -0.21 0.14 9.84 3.6 0.74 0.44 154.54 189 2.32 180 850135210 0.75 0.99 18.21 178.03 0.55 0.15 0.17 0.01 noise 0 55.11 0.02 -0.12 0.28
951764724 10.5901 70 -0.34 0.18 10.59 4.24 0.97 0.41 130.7 191 2.78 181 850135212 0.31 0.99 6.04 149.58 0.48 0.3 0.01 0 good 0 65.46 0 -0.09 0.04
951764731 12.0302 50 0.34 0.16 12.03 5.05 0.96 0.59 99.59 192 2.16 182 850135212 0.18 0.99 10.22 230.73 0.23 0.32 0.04 0.01 good 1.72 88.04 0 -0.05 0.06
951764739 1.05082 80 0.2 0.03 1.05 3.43 0.07 0.55 99.4 193 2.24 183 850135212 0.09 0.89 28.31 142.88 0.27 0.32 0.1 0 noise 1.72 25.5 0.04 -0.04 0
951764746 0.00227 170 -0.54 0.1 0 4.6 nan 0.54 120.51 194 0.88 184 850135170 0.18 0.18 nan 0 0.47 0.22 0.01 0 noise 0.23 8.69384e+12 nan -0.2 0
951764753 9.52085 100 -0.76 0.05 9.52 nan nan 1.47 81.66 195 1.14 185 850135214 2.19 0.99 73.81 363.01 0.05 1.87 0.5 nan good 0 nan 0 -0.02 0.6
951764761 8.88574 90 -0.18 0.07 8.89 nan nan 1.55 80.33 196 0.51 186 850135214 3.12 0.99 80.94 522.26 0.02 nan 0.32 0 noise -0.2 nan nan nan 1.07
951764768 9.13933 30 -4.12 0.13 9.14 5.07 0.94 1.65 124.5 197 1.88 187 850135214 1.29 0.99 12.05 218.02 0.07 0.67 0.03 0.01 good 3.43 75.02 0.01 -0.06 0.06
951764776 3.37133 40 -0.34 0.12 3.37 nan nan 1.19 168.29 198 1.75 188 850135216 4.85 0.99 13.94 272.98 0.13 0.95 0.03 0 good 0.69 nan nan -0.01 0.34
951764783 23.1542 60 -0.34 0.12 23.15 nan nan 1.8 108.62 199 1.16 189 850135216 5.81 0.99 21.1 281.45 0.07 nan 0.06 0 good 0 nan nan -0.01 0.01
951764791 5.49003 40 -0.34 0.03 5.49 nan nan 1.24 215.03 200 2.34 190 850135216 2.86 0.99 17.19 176.86 0.17 0.85 0 0 good 0 nan nan -0.01 0.04
951764798 10.1731 140 0.15 0.02 10.17 nan nan 1.09 44.36 201 0.33 191 850135216 1.44 0.88 112.47 900.56 0.01 nan 0.5 nan good 0.19 nan 0 nan 0.22
951764809 20.4946 100 0.45 0.06 20.49 nan nan 0.96 88.46 202 0.55 192 850135218 0.12 0.99 100.51 745.32 0.16 0.93 0.5 nan noise 3.66 nan 0 -0 0.28
951764815 0.83423 40 0.14 0 0.83 2.52 0.33 1.55 87.73 203 0.67 193 850135220 6.78 0.99 19.38 250.21 0.04 nan 0.5 0 noise nan 30.85 0.03 nan 0.39
951764821 0.83144 60 -0.33 0.03 0.83 nan nan 1.48 93.33 204 1.25 194 850135220 13.11 0.99 23.91 360.76 0.06 nan 0.5 nan noise nan nan 0 -0 0.45
951764827 0.0031 170 0.22 nan 0 nan 1 1.32 71.84 205 0.67 195 850135196 0.8 0.18 nan 0 0.11 1.32 0.5 nan noise -0.09 nan nan -0.03 0
951764835 9.1322 170 1.03 0.01 9.13 nan nan 2.1 18.21 206 0.18 196 850135270 1.31 0.99 134.42 1226.98 0.01 0.47 0.5 0 noise -1.97 nan nan -0.03 0.92
951764842 2.50341 60 0.69 0.12 2.5 3.24 0.77 0.56 52.04 207 0.71 197 850135318 0.39 0.99 35.89 522.61 0.11 1 0.5 0.01 good 0.46 42.86 0.09 -0 6.18
951764848 0.71105 70 0.69 0.23 0.71 3.24 0.81 1.68 152.11 208 1.68 198 850135324 2.57 0.99 30.32 279.83 0.03 nan 0 0 good 2.01 43.36 0.02 -0.03 1.46
951764855 4.23894 100 0.89 0.08 4.24 2.84 0.87 0.76 62.2 209 1.43 199 850135332 0.38 0.99 34.3 386.55 0.17 0.23 0.42 0.01 good 2.58 48.46 0.03 -0.02 1.2
951764862 2.10123 60 0.34 0.19 2.1 3.77 0.88 0.47 107.69 210 2.09 200 850135334 0.2 0.99 27.73 146.3 0.38 0.22 0.01 0 good 0.96 51.56 0.01 -0.03 0.19
951764868 13.3805 70 0 0.17 13.38 4.07 0.97 0.32 114.51 211 2.43 201 850135334 0.33 0.99 40.84 106.77 0.45 0.15 0.01 0.02 good 0.21 77.68 0.01 -0.1 0.07
951764875 1.47967 70 0.96 0.16 1.48 4.41 0.91 0.76 139.71 212 2.7 202 850135334 0.16 0.99 38.05 250.14 0.46 0.22 0.01 0 good 1.65 49.67 0.01 -0.02 0.85
951764883 3.91798 170 0.84 0.06 3.92 2.83 0.47 0.66 30.22 213 0.64 203 850135338 0.49 0.99 39.03 698.98 0.03 1.3 0.5 0.02 noise 1.13 31.63 0.09 -0.02 1.67
951764889 7.6392 170 -0.4 0.1 7.64 4.4 0.94 0.92 18.94 214 0.43 204 850135338 0.63 0.99 58.52 1128.71 0.01 nan 0.5 0 noise -1.82 60.31 0.02 -0.01 0.57
951764895 5.06408 90 -0.75 0.11 5.06 3.45 0.9 0.27 66.73 215 1.69 205 850135340 0.6 0.99 47.03 320.29 0.28 0.12 0.08 0.01 good 0.48 52.68 0.02 -0.01 0.12
951764903 6.99842 70 -0.69 0.16 7 4.24 0.95 0.54 88.92 216 2.45 206 850135340 0.56 0.99 38.71 114.38 0.27 0.22 0.01 0.01 good 0.48 67.34 0.01 -0.03 0.08
951764909 3.95053 60 0 0.07 3.95 2.51 0.91 0.92 87.78 217 2.13 207 850135340 0.43 0.99 33.65 240.48 0.2 0.21 0.5 0 noise 2.82 50.2 0.02 -0.02 0.02
951764916 0.01033 150 -5.08 nan 0.01 3.69 0 0.71 75.75 218 1.75 208 850135340 0.69 0.54 nan 0 0.17 0.23 0.5 0 noise 0.17 36.23 0 -0.04 0
951764923 0.00558 170 -0.24 nan 0.01 4.02 nan 0.81 65.82 219 1.31 209 850135340 0.48 0.39 nan 0 0.17 0.29 0.38 0 noise 1.98 56.03 0 -0.02 0
951764928 0.00765 120 0.69 nan 0.01 3.98 nan 0.71 90.28 220 1.97 210 850135340 0.34 0.36 nan 0 0.24 0.19 0.38 0 noise 1.57 30.19 0 -0.03 0
951764935 0.01354 120 -0.07 nan 0.01 3.24 0 0.6 76.25 221 1.75 211 850135340 0.67 0.63 nan 0 0.21 0.22 0.5 0 noise 1.13 25.74 0 -0.03 0
951764939 0.00827 140 -2.55 nan 0.01 3.41 nan 0.69 85.12 222 1.91 212 850135340 0.44 0.51 nan 0 0.24 0.21 0.46 0 noise 2.19 27.52 0 -0.01 0
951764944 4.10667 120 -0.37 0.08 4.11 2.76 0.71 0.32 65.35 223 1.09 213 850135342 0.17 0.99 42.39 350.63 0.27 0.8 0.5 0.01 noise -0.01 42.39 0.05 -0.04 2.35
951764951 2.11601 60 -0.1 0.05 2.12 nan nan 0.96 94.86 224 1.72 214 850135342 0.11 0.99 46.58 1667.7 0.07 0.71 0.49 0 good -0.69 nan nan -0.01 0.09
951764958 2.80133 120 0.78 0.01 2.8 2.87 0.69 1.1 30.85 225 0.39 215 850135344 0.49 0.99 59.48 1235.88 0.01 nan 0.5 0.06 noise 1.05 66.99 0.02 nan 0.16
951764964 4.36522 120 1.18 0.03 4.37 1.94 0.38 1.14 30.17 226 0.25 216 850135326 1.77 0.92 79.98 675.41 0 nan 0.23 0.04 noise -0.56 35.29 0.07 -0.01 0.08
951764971 1.73925 120 -0.51 0.02 1.74 3.14 0.49 0.65 40.53 227 0.45 217 850135344 0.62 0.75 68.39 586.07 0.04 nan 0.34 0.01 noise -0.54 36.95 0.04 -0.04 0.27
951764977 3.93389 160 -0.44 0.02 3.93 2.41 0.35 0.88 27.64 228 0.38 218 850135344 0.42 0.99 83.86 1007.86 0.03 1.36 0.5 0.03 noise 1.12 36.67 0.07 -0.01 0.15
951764983 3.26614 170 -1.48 -0.06 3.27 nan nan 1.02 31.53 229 0.26 219 850135326 1.64 0.99 38.25 1008.08 0.03 nan 0.5 0 noise -1.4 nan nan -0.02 0.17
951764990 1.58476 170 2.39 0.02 1.58 nan nan 0.96 24.14 230 0.4 220 850135344 0.29 0.99 74.77 1473.81 0.01 nan 0.5 0 noise 1.58 nan nan -0 6.56
951764995 1.82656 140 1.16 0.03 1.83 3.27 0.47 1.03 43.89 231 0.64 221 850135344 0.53 0.62 43.18 609.47 0.02 nan 0.19 0.03 noise 1.43 43.98 0.04 nan 0.14
951765001 0.65494 170 1.03 -0 0.65 1.35 0.04 1.5 28.63 232 0.39 222 850135344 0.63 0.66 34.41 608.55 0.02 nan 0.5 0.01 noise -2.25 21.23 0.21 -0.1 2.62
951765009 18.7407 30 0 0.18 18.74 7.7 1 0.49 173.8 233 3.44 223 850135356 0.06 0.99 34.7 55.38 0.65 0.16 0 0 good 1.37 124.54 0 -0.06 0
951765017 1.72437 160 -3.95 0.03 1.72 nan nan 2.47 45.76 234 0.69 224 850135372 4.91 0.99 67.1 1747.95 0.04 1.33 0.48 0 noise 2.67 nan nan nan 2.76
951765023 2.14391 60 0 0.12 2.14 6.34 0.98 0.58 120.35 235 1.8 225 850135374 0.14 0.99 27.18 212.42 0.41 0.19 0.02 0 good -0.96 69.21 0 -0.04 0.15
951765031 6.40951 140 2.33 -0.01 6.41 1.22 0.33 1 27.72 236 0.28 226 850135368 2.09 0.99 66.78 819.7 0.04 1.39 0.5 0.16 noise -1.16 36.92 0.22 -0.01 0.11
951765039 6.89932 140 2.37 0 6.9 1 0.38 2.2 25.64 237 0.25 227 850135368 1.95 0.99 87.73 1010.54 0 nan 0.37 0.15 noise -0.03 38.77 0.21 -0.38 0.08
951765044 6.80167 120 2.05 -0 6.8 2.41 0.5 1.04 38 238 0.31 228 850135368 4.18 0.99 89.46 968.25 0.01 1.14 0.5 0.05 noise -1.64 45.06 0.06 -0.01 0.08
951765049 0.0031 80 0.41 nan 0 3.47 nan 0.69 240.3 239 2.63 229 850135370 0.4 0.18 nan 0 0.95 0.14 0.01 0 noise 1.44 1.40477e+13 nan -0.07 0
951765055 0.04092 40 0.69 nan 0.04 2.32 0.29 0.65 205.41 240 2.46 230 850135370 0.46 0.77 8.3 3.5 0.82 0.14 0.34 0 noise 1.03 27.43 0.05 -0.07 0
951765061 0.04764 70 0 nan 0.05 6.2 0.91 0.62 321.87 241 4.77 231 850135372 0.22 0.69 9.68 13.22 1.13 0.11 0 0 good 1.18 42.23 0 -0.12 0
951765067 1.06364 100 0.16 0.05 1.06 2.1 0.66 0.66 62.35 242 0.95 232 850135372 0.62 0.99 55.37 454.97 0.23 0.16 0.5 0.01 good -2.2 35.52 0.09 -0.01 2.57
951765074 0.86037 70 0.34 0.01 0.86 3.49 0.51 0.22 133.16 243 1.75 233 850135372 0.37 0.96 27.8 124.64 0.57 0.12 0.5 0.01 noise -0.76 36.03 0.08 -0.07 14.96
951765080 3.61148 160 -3.12 -0.03 3.61 1.89 0.51 0.03 62.79 244 0.71 234 850135376 1.93 0.99 33.71 415.94 0.6 nan 0.5 0.03 noise 3.24 29.56 0.36 nan 3.62
951765085 0.00713 80 -0.34 nan 0.01 2.55 0 0.7 203.93 245 1.79 235 850135372 0.2 0.4 nan 0 0.62 0.16 0.35 0 noise 4.43 35.61 0 -0.04 0
951765093 0.0125 30 0.69 nan 0.01 7 0.56 0.63 715.89 246 2.7 236 850135376 0.69 0.49 nan 0 0.74 0.11 0.31 0 noise nan 69.88 0 -0.12 0
951765098 0.62353 80 0.62 0.07 0.62 4.45 0.61 0.65 96.24 247 1.8 237 850135380 0.13 0.99 34.92 552.24 0.35 0.18 0.12 0 good 2.27 34.89 0.07 -0.03 3.39
951765105 17.799 120 -2.42 -0.01 17.8 nan nan 1.19 39.68 248 0.18 238 850135368 2.37 0.99 53.48 788.29 0.01 nan 0.37 0 noise 1.15 nan nan nan 0.19
951765110 3.41453 160 0.05 0.01 3.41 2.5 0.69 0.04 44.13 249 0.49 239 850135376 12.17 0.99 30.93 679.96 0.38 nan 0.5 0.02 noise -0.93 43.2 0.09 nan 1.6
951765118 1.60491 150 4.32 -0.01 1.6 nan nan 2.02 47.36 250 0.52 240 850135388 32.09 0.99 50.88 1546.16 0.01 1.62 0.46 0 noise -9.75 nan nan -0.76 1.82
951765124 10.2191 120 -3.34 0.03 10.22 nan nan 1.06 36.19 251 0.31 241 850135368 3.68 0.99 27.06 457.71 0.01 nan 0.5 0 noise 1.23 nan nan nan 0.06
951765132 6.29749 120 1.21 0.03 6.3 1.77 0.25 1.07 41.41 252 0.38 242 850135390 1.21 0.99 67.16 800.86 0.05 0.8 0.5 0.05 noise -0.01 33.52 0.2 -0.01 0.08
951765138 4.64836 160 -2.88 -0 4.65 1.42 0.21 0.91 34.52 253 0.3 243 850135390 0.08 0.99 76.98 1010.7 0.02 nan 0.5 0.06 noise -0.84 33.01 0.17 nan 0.13
951765145 5.76635 80 0 0.11 5.77 5.83 0.99 0.55 112.37 254 1.17 244 850135390 0.31 0.99 33.48 140.59 0.37 0.19 0.02 0 good -4.33 65.76 0 -0.05 0.03
951765151 12.9111 40 -0.69 0.11 12.91 6.16 1 0.36 174.67 255 2.67 245 850135416 0.27 0.99 39.63 72.37 0.7 0.15 0.01 0 good 0.69 82.53 0 -0.04 0.01
951765159 25.3179 100 1.17 -0 25.32 1.86 0.76 1.57 34.79 256 0.1 246 850135424 1.84 0.99 33.89 464.32 0 nan 0.19 0.19 noise -3.31 94.62 0.12 -0.01 0.13
951765164 8.99611 170 -1.01 0.06 9 3.33 0.92 1.59 55.43 257 0.48 247 850135418 1.76 0.99 48.51 282.37 0.02 nan 0.5 0.07 noise 0.84 100.29 0.04 nan 1.33
951765170 5.02088 170 0.1 0.02 5.02 nan nan 2.02 31.36 258 0.23 248 850135430 0.79 0.99 54.83 754.73 0 nan 0.5 0 noise -0.19 nan nan -0.03 0.6
951765176 2.50662 70 -0.55 0.04 2.51 3.43 0.8 0.41 91.38 259 1.43 249 850135430 0.3 0.99 24.52 323.88 0.33 0.88 0.5 0.02 good -0.41 49.23 0.05 -0.03 1.87
951765182 10.2026 140 1.35 0.04 10.2 2.94 0.95 0.87 40.75 260 0.11 250 850135430 0.91 0.99 54.31 516.35 0.02 nan 0.5 0.03 good 2.98 82.95 0.01 -0.01 0.38
951765189 3.2618 100 -2.29 0.01 3.26 nan nan 0.93 44.59 261 0.47 251 850135426 4.06 0.98 27.44 302.37 0.02 nan 0.5 0 noise 2.4 nan nan nan 0.56
951765195 0.83537 170 0.57 -0.05 0.84 1.8 0.21 1.54 63 262 0.5 252 850135418 2.73 0.97 31.34 177.79 0.03 nan 0.5 0.02 noise 4.45 27.92 0.19 nan 21.15
951765200 0.81367 170 -0.79 0.05 0.81 2.6 0.37 0.96 45.71 263 0.54 253 850135450 5.67 0.99 79.05 876.67 0.03 nan 0.24 0 noise 5.15 28.74 0.12 nan 22.76
951765206 0.65071 130 -2.2 0.12 0.65 3.79 0.72 0.77 77.28 264 1.09 254 850135444 0.35 0.99 45.69 476.49 0.11 0.36 0.04 0 noise -1.02 28 0.1 -0.01 15.46
951765213 0.47751 50 0.34 0.12 0.48 4.18 0.98 1.47 120.86 265 1.57 255 850135450 1.97 0.99 61.81 131.62 0.07 nan 0 0 good 1.03 61.9 0 nan 0
951765219 0.00651 170 -3.23 nan 0.01 4.35 0 1.24 151.56 266 0.97 256 850135460 0.7 0.34 nan 0 0.27 0.27 0.5 0 noise -1.76 35.5 0 -0.04 0
951765225 5.07885 130 -3.71 0.16 5.08 3.02 0.92 0.73 63.69 267 1.3 257 850135454 0.16 0.99 28.04 430.28 0.15 0.32 0.34 0.01 good -0.78 53.42 0.04 -0.02 1.4
951765231 2.53317 100 -1.9 0.06 2.53 2.41 0.64 0.81 55.35 268 0.74 258 850135470 0.11 0.99 43.21 544.27 0.16 0.55 0.23 0.03 noise 0.14 48.87 0.03 -0.01 0.27
951765238 2.03313 120 -4.4 0.02 2.03 2.19 0.45 0.45 41.71 269 0.68 259 850135452 5.59 0.99 60.02 654.48 0.07 0.6 0.34 0.02 noise -1.11 33.45 0.1 -0.04 0.68
951765243 5.11461 100 -1.37 0.06 5.11 2.67 0.87 0.67 91.63 270 1.57 260 850135460 0.81 0.99 65.38 409.3 0.23 0.21 0.01 0.01 good -0.66 54.71 0.02 -0.02 0.45
951765247 7.2672 150 -2.46 0.06 7.27 1.62 0.69 1 57.28 271 0.64 261 850135470 0.17 0.99 82.77 343.01 0.08 0.45 0.5 0.02 noise 0.02 42.76 0.04 -0.03 1.05
951765252 4.16857 120 -1.44 0.1 4.17 3.6 0.85 0.89 151.42 272 1.77 262 850135470 0.14 0.99 64.42 347.29 0.43 0.25 0 0.01 good 0.14 40.98 0.05 -0.02 0.44
951765258 9.5782 80 -2.67 0.08 9.58 2.63 0.81 0.93 81.69 273 0.95 263 850135470 0.07 0.99 56.75 226.82 0.18 0.29 0.4 0.03 good 0.34 51.31 0.05 -0 0.21
951765264 2.62855 90 -0.77 0.19 2.63 4.22 0.93 0.87 196.8 274 2.09 264 850135478 0.36 0.99 63.37 347.09 0.56 0.19 0 0 good 1.99 59.42 0 -0.04 0.11
951765270 2.10805 70 0.69 0.08 2.11 3.48 0.95 0.34 103.97 275 1.68 265 850135466 0.87 0.99 38.91 270.23 0.45 0.14 0.41 0 good 0.76 55.06 0 -0.08 0.48
951765276 6.53124 100 -1.92 0.02 6.53 2.23 0.65 0.78 105.64 276 1.28 266 850135470 0.15 0.99 80.68 300.26 0.26 0.29 0.47 0.02 good -0.14 38.09 0.06 -0.02 0.5
951765282 2.79348 80 -1.03 0.19 2.79 6.02 0.99 0.77 262.93 277 3.2 267 850135470 0.21 0.99 67.61 221.04 0.79 0.18 0 0 good 0.21 76.77 0 -0.08 0
951765288 9.12827 50 -0.76 0.09 9.13 3.9 1 1.07 284.26 278 1.16 268 850135474 0.12 0.99 23.62 74.75 0.27 0.33 0 0 good -0.69 83.49 0 -0 0
951765293 5.05044 70 -0.62 0.12 5.05 3.69 0.99 0.73 173.58 279 2.45 269 850135472 0.15 0.99 50.96 209.01 0.55 0.16 0 0 good -0.89 72.1 0 -0.04 0.04
951765299 4.3677 70 -1.03 0.16 4.37 6.08 0.98 0.8 274.42 280 2.88 270 850135474 0.01 0.95 47.48 147.52 0.72 0.19 0 0 good -0.21 93.52 0 -0.01 0.04
951765303 6.53413 140 -1.84 0.03 6.53 1.58 0.56 0.87 46.29 281 0.46 271 850135478 0.63 0.99 94.98 383.23 0.08 0.29 0.38 0.02 good -0.2 34.5 0.06 -0.01 0.71
951765309 2.50352 70 -0.26 0.12 2.5 3.63 0.93 0.87 141.18 282 1.44 272 850135478 0.28 0.99 39.07 325.75 0.32 0.25 0.01 0 good -0.69 61.33 0 -0.04 0.15
951765314 9.83788 70 -1.74 0.07 9.84 3.74 0.96 0.87 111.1 283 1.27 273 850135478 0.24 0.99 70.31 149.92 0.33 0.15 0.02 0 good 0.34 65.22 0 -0.03 0.07
951765319 0.90471 70 -0.76 0.11 0.9 4.06 0.88 1.03 280.94 284 3.71 274 850135474 0.02 0.99 34.51 137.07 1 0.16 0 0 good -0.69 48.25 0 -0.03 0.09
951765323 3.66574 50 -0.69 -0.02 3.67 3.32 1 1.17 171.31 285 2.26 275 850135476 0 0.99 65.95 88.59 0.63 0.22 0 0 good 0.69 51.45 0.01 -0.05 0
951765329 4.50648 90 -1.18 0.1 4.51 2.84 0.82 0.96 97.5 286 1.49 276 850135476 0.04 0.96 56.93 218.51 0.29 0.26 0.05 0 good -1.03 48.39 0.01 -0.03 0.33
951765334 6.26566 70 -1.24 0.11 6.27 3.12 0.83 0.91 123.72 287 1.32 277 850135476 0.13 0.99 49.78 215.26 0.24 0.4 0.04 0 good -1.37 40.5 0.03 -0.02 0.98
951765339 1.33551 60 -1.1 0.07 1.34 4.55 0.88 0.8 241.56 288 2.99 278 850135480 0.31 0.99 72.34 214.3 0.63 0.14 0 0 good -0.69 53.86 0 -0.02 0.61
951765343 4.19781 70 -0.27 0.05 4.2 2.45 0.76 0.8 149.07 289 1.49 279 850135478 0.39 0.99 70.01 267.93 0.44 0.18 0.5 0.01 good 0 32.01 0.06 -0.03 1.05
951765349 10.8901 60 -0.69 0.11 10.89 3.44 0.98 0.7 188.92 290 2.1 280 850135478 0.36 0.99 61.77 214.53 0.57 0.14 0.01 0 good 0 66.33 0 -0.03 0.02
951765353 3.54545 110 -0.98 -0.01 3.55 1.79 0.81 0.89 71.82 291 1.02 281 850135480 0.08 0.99 63.94 311.37 0.2 0.25 0.1 0 good -0.62 41.48 0.02 -0.01 0.32
951765358 2.30501 80 -0.21 0.12 2.31 3.58 0.82 0.82 187.19 292 1.5 282 850135478 0.35 0.99 53.6 291.9 0.44 0.14 0 0 good 1.1 50.1 0 -0.04 0.15
951765364 39.3285 60 -0.27 0.06 39.33 4.18 1 0.26 181.77 293 2.62 283 850135482 0.54 0.99 64.71 91 0.81 0.16 0 0 good 0.69 81.96 0 -0.15 0
951765369 13.1377 70 -0.81 0.06 13.14 2.8 0.86 0.93 90.77 294 1.44 284 850135484 0.06 0.99 58.87 239.58 0.32 0.16 0.33 0.01 good nan 48.22 0.03 -0.01 0.4
951765374 0.32385 150 -2.14 0.02 0.32 2.53 0.1 1.47 179.54 295 0.77 285 850135478 0.72 0.99 57.11 291.03 0.07 0.99 0.11 0 noise -0.12 13.73 0.26 -0.08 191.29
951765379 2.20085 160 -0.65 0.01 2.2 2.33 0.19 1 71.64 296 0.46 286 850135478 1.68 0.99 80.64 763.1 0.03 1.55 0.36 0 noise 0.21 22.79 0.13 nan 14.53
951765385 0.00785 110 0.41 nan 0.01 3.99 nan 0.41 147.87 297 0.82 287 850135476 0.01 0.48 nan 0 0.45 0.22 0.4 0 good -0.62 27.41 0 -0.06 0
951765393 5.09063 160 -0.55 0.1 5.09 3.25 0.91 1.59 68.23 298 0.62 288 850135478 2.98 0.99 62.81 413.66 0.05 0.95 0.5 0 noise 0.65 49.39 0.01 nan 1.06
951765396 0.00289 160 -0.42 nan 0 4.32 nan 0.63 181.48 299 0.94 289 850135492 2.64 0.22 nan 0 0.04 nan 0.5 0 noise -1.02 2.85682e+12 nan nan 0
951765400 16.8106 140 3.02 0.04 16.81 2.98 0.81 1.19 40.22 300 0.29 290 850135494 1.42 0.99 46.83 492.07 0.02 nan 0.17 0.01 noise -2.51 60.96 0.02 -0.02 0.04
951765405 33.1885 80 -1.24 0.09 33.19 5.87 0.99 1.85 196.94 301 1.51 291 850135494 4.73 0.99 59.55 115.09 0.16 nan 0 0 good 0.62 85.28 0 nan 0.01
951765411 11.0497 130 -0.48 0.06 11.05 3.45 0.86 1 36.4 302 0.26 292 850135494 1.34 0.99 50.74 566.45 0.01 nan 0.45 0.01 noise 1.41 58.97 0.01 nan 0.11
951765414 5.89448 40 0.69 0.13 5.89 3.91 0.98 0.51 223.72 303 3.06 293 850135496 0.62 0.99 52.33 71.63 0.79 0.15 0 0 good 0.34 72.96 0 -0.08 0
951765420 13.1448 70 0.41 0.09 13.14 2.81 0.99 0.34 84.18 304 1.81 294 850135498 0.22 0.99 49.98 111.26 0.35 0.21 0.02 0 good 0.21 71.9 0 -0.06 0.01
951765423 14.1916 100 -0.35 0.1 14.19 3.32 0.98 0.44 59.55 305 1.73 295 850135500 0.54 0.99 45.27 140.5 0.23 0.18 0.19 0 good 0.2 82.86 0 -0.04 0.07
951765430 5.69876 110 -2.96 0.07 5.7 3.1 0.95 0.6 96.35 306 2.2 296 850135504 0.13 0.99 64.15 110.91 0.36 0.16 0 0 good 0.27 48.63 0.03 -0.02 0.11
951765435 19.8853 80 0 0.12 19.89 6.01 1 0.22 163.91 307 3.01 297 850135506 0.19 0.99 63.13 97.65 0.69 0.14 0 0 good 0 89.4 0 -0.16 0.02
951765440 9.97935 80 -3.57 0.06 9.98 1.95 0.5 0.36 65.64 308 1.24 298 850135520 0.97 0.99 56.14 917.5 0.15 0.22 0.37 0.02 good 0.41 40.54 0.06 -0.01 0.09
951765447 1.86221 60 -0.14 0.03 1.86 2.63 0.42 0.26 41.79 309 1.1 299 850135522 2.21 0.99 74.83 1479.83 0.19 0.14 0.5 0.01 good 0 32.71 0.04 -0.03 0.93
951765454 5.47349 130 0.67 0.02 5.47 2.72 0.49 1.3 48.24 310 0.81 300 850135526 0.48 0.98 51.92 1069.77 0 nan 0.46 0.02 good -0.29 36.22 0.05 nan 0.23
951765460 4.44892 70 -0.21 0.1 4.45 4.46 0.98 0.81 71.54 311 0.95 301 850135526 0.46 0.99 52.25 226.24 0.17 1.29 0.43 0 good -0.21 58.94 0 -0.01 0.23
951765467 9.98162 30 0 0.24 9.98 4.45 0.96 0.16 314.61 312 4.9 302 850135528 0.68 0.77 13.32 98.02 1.08 0.08 0 0 good 0 63.59 0.01 -0.48 0.01
951765473 4.10409 40 0 0.06 4.1 2.8 0.94 0.16 113.73 313 1.72 303 850135528 4.91 0.6 28.21 319.21 0.36 0.14 0.5 0 noise 6.18 69.04 0 -0.06 0.25
951765478 17.4047 30 6.52 0.07 17.4 2.4 0.78 1.41 131.76 314 1.8 304 850135532 0.57 0.97 18.69 170.53 0.01 nan 0.02 0.03 good nan 48.68 0.07 nan 0.61
951765485 13.9773 40 1.72 0.04 13.98 2.52 0.8 1.54 167.8 315 1.97 305 850135532 0.87 0.99 37.84 276.76 0.03 nan 0.5 0.03 good nan 46.45 0.07 nan 0.13
951765490 5.27323 20 nan 0.16 5.27 5.02 0.97 0.18 276.16 316 1.62 306 850135528 9.85 0.69 34.6 372.84 0.26 0.19 0.09 0 noise -0.69 59.62 0 -0.13 0.03
951765497 8.33011 30 1.37 0.02 8.33 1.85 0.42 1.58 129.34 317 1.72 307 850135532 0.56 0.99 70.69 594.95 0.02 nan 0.43 0.03 noise -15.8 34.59 0.09 nan 0.5
951765502 13.287 60 3.88 0.02 13.29 1.94 0.7 0.88 74.88 318 0.9 308 850135532 0.28 0.99 19.79 390.99 0.03 nan 0.41 0.05 noise -2.97 46 0.07 -0.01 0.26
951765508 2.13461 50 -0.21 0.05 2.13 4.76 0.89 0.74 123.99 319 1.73 309 850135532 0.16 0.99 65.81 206.29 0.35 0.43 0.01 0 good 2.75 49.17 0.01 -0.01 0.03
951765513 3.90661 20 -0.69 0.08 3.91 5.43 0.95 0.73 92.38 320 2.58 310 850135534 5.24 0.85 60.19 556.47 0.23 0.1 0.16 0 noise nan 63.22 0 -0.01 0.02
951765520 24.5397 150 3.15 0.01 24.54 nan nan 1.22 40.54 322 0.23 311 850135538 1.26 0.99 56.65 489.06 0 nan 0.5 0 noise 1 nan nan -0 0.23
951765525 12.0324 160 -2.46 0.03 12.03 2.12 0.49 1.04 43.27 323 0.21 312 850135538 1.34 0.87 49.35 407.97 0.02 nan 0.5 0.04 noise -0.48 45.74 0.05 nan 0.41
951765530 2.95127 80 0.14 0.1 2.95 4.1 0.87 0.65 96.61 324 1.98 313 850135540 0.86 0.99 57.93 449.71 0.21 0.21 0 0 good 0.76 42.12 0.02 -0.03 0.18
951765535 3.3674 40 nan 0.1 3.37 3.79 0.88 0.63 102.58 325 2.06 314 850135540 0.85 0.99 35.02 174.93 0.3 0.19 0.04 0.01 good 0.34 49.14 0.01 -0.04 0.16
951765541 1.58972 70 -0.34 0.08 1.59 3.35 0.62 1.26 84.77 326 0.47 315 850135538 1.76 0.99 39.98 297.02 0.02 nan 0.06 0 good 0.62 34.71 0.03 -0.03 0.41
951765547 3.5935 70 0 0.12 3.59 2.37 0.55 0.26 111.7 327 2.55 316 850135542 0.44 0.99 43.52 167.28 0.49 0.18 0.02 0 good 0.12 37 0.05 -0.09 0.08
951765552 2.32971 100 -0.55 0.08 2.33 3.21 0.69 0.67 80.97 328 2.02 317 850135542 0.29 0.99 37.02 291.49 0.23 0.23 0.35 0.01 good 2.06 43.01 0.02 -0.02 0.51
951765557 4.0796 100 0 0.1 4.08 4.25 0.88 0.98 79.39 329 0.47 318 850135538 1.95 0.99 47.98 203.49 0.06 nan 0.5 0.01 good 0.26 62.88 0 -0 0.13
951765561 1.76766 60 0.69 0.06 1.77 4.46 0.93 0.67 106.44 330 1.84 319 850135546 0.01 0.94 48.54 106.04 0.29 0.32 0.02 0 good 1.3 43.06 0.01 -0.04 7.59
951765566 3.18388 40 0.34 0.08 3.18 3.57 0.8 0.66 139.12 331 2.36 320 850135548 0.01 0.96 39.89 127.15 0.38 0.3 0.02 0 good 2.06 47.13 0.02 -0.04 0.13
951765571 2.77426 70 0.14 0.12 2.77 4.01 0.82 0.59 136.85 332 2.68 321 850135550 0.98 0.99 39.4 257.24 0.38 0.15 0.01 0 good 1.79 43.14 0.02 -0.06 0.32
951765576 12.7688 20 nan 0.13 12.77 2.84 0.88 0.3 154.56 333 3.07 322 850135550 0.83 0.99 56.81 110.93 0.63 0.12 0.06 0.02 noise -0.69 56.65 0.03 -0.11 0.04
951765582 14.778 60 0 0.05 14.78 3.51 0.86 0.22 170.34 334 3.49 323 850135550 0.91 0.99 52.15 105.33 0.74 0.1 0.01 0.02 good 0.21 59.1 0.03 -0.19 0.05
951765587 2.62793 120 0 0.11 2.63 4.05 0.95 0.65 78.83 335 2.14 324 850135552 0.18 0.99 18.69 192.15 0.3 0.16 0.06 0 good 1.48 55.83 0 -0.04 0.13
951765594 2.76868 140 -0.14 0.09 2.77 3.01 0.75 0.41 72.44 336 1.33 325 850135548 0.14 0.99 50.71 305.21 0.27 0.37 0.5 0 good 0.45 43.45 0.02 -0.03 0.82
951765600 0.00796 170 0.37 nan 0.01 3.56 nan 1.24 107.16 337 1.02 326 850135558 4.81 0.52 nan 0 0.08 nan 0.5 0 noise 0.02 35.83 0 -0.02 0
951765606 7.46973 50 0 0.1 7.47 4.84 0.96 1.35 127.65 338 1.56 327 850135564 6.27 0.99 30.61 151.59 0.05 nan 0.03 0 good 1.03 75.46 0 -0.01 0.2
951765611 23.9673 60 0 0.13 23.97 3.71 0.98 0.73 168.07 339 1.96 328 850135566 0 0.99 58.3 152.94 0.34 0.41 0 0.01 good 0.82 117.66 0 -0.05 0.01
951765617 2.60169 80 0.34 0.1 2.6 2.42 0.64 0.62 113.92 340 1.38 329 850135566 0.17 0.99 37.35 442.26 0.3 0.38 0.33 0 good 1.24 43.65 0.02 -0.04 0.26
951765623 6.50075 90 0.27 0.12 6.5 3.56 0.95 0.7 107.6 341 2.27 330 850135568 0.1 0.99 42.9 184.27 0.34 0.21 0.01 0 good 1.57 66.4 0 -0.02 0.07
951765629 3.00129 60 1.37 0.25 3 4.96 0.98 0.6 379.77 342 5.43 331 850135570 0.44 0.97 30.83 97.69 1.08 0.16 0 0 good 0.82 65.17 0 -0.14 0
951765635 0.11336 50 4.12 nan 0.11 3.8 0.19 0.89 162.18 343 1.75 332 850135570 0.62 0.73 26.07 172.34 0.39 0.41 0.1 0 noise 1.17 32.51 0.01 -0.04 0
951765641 4.34527 80 0 0.12 4.35 3.23 0.71 0.6 165.25 344 2.7 333 850135572 0.63 0.99 26.61 259.8 0.45 0.19 0.15 0 good 0.61 41.47 0.03 -0.05 0.26
951765647 9.12497 90 0.69 0.18 9.12 4.87 0.94 1.43 197.3 345 2.46 334 850135574 6.69 0.99 34.73 114.37 0.08 nan 0.01 0 good 1.52 65.29 0.01 -0.01 0.01
951765653 9.42195 70 0 0.07 9.42 3.89 0.99 0.81 111.19 346 1.81 335 850135576 0.42 0.99 45.01 115.34 0.34 0.15 0.11 0 good 3.09 78.11 0 -0.03 0.01
951765661 15.6626 110 0.62 0.15 15.66 4.43 0.97 0.56 178.05 347 1.99 336 850135578 0.47 0.99 59.73 102.87 0.43 0.26 0 0 good 0.34 72.23 0.01 -0.09 0.02
951765666 9.72245 100 -6.32 0 9.72 1.84 0.58 0.27 71.6 348 1.09 337 850135576 0.78 0.99 80.13 259.35 0.32 0.14 0.24 0.01 good -0.2 39.77 0.07 -0.03 0.33
951765669 5.41325 80 0.21 0.1 5.41 2.49 0.75 0.66 128.98 349 2.77 338 850135580 0.32 0.99 64.93 158.97 0.41 0.21 0.06 0 good 0.82 39.66 0.04 -0.05 0.1
951765675 18.6652 90 -0.41 0.04 18.67 3.91 0.94 0.21 119.65 350 2.52 339 850135580 0.52 0.99 59.94 172.66 0.51 0.12 0.18 0.02 good -0.31 78.77 0.01 -0.15 0.03
951765681 14.6917 130 0.82 0.07 14.69 2.77 0.88 0.55 97.06 351 2.24 340 850135580 0.39 0.99 57.46 140.99 0.26 0.26 0.5 0.03 good 0.94 59.98 0.02 -0.03 0.09
951765686 11.2814 130 0.27 0.08 11.28 3.25 0.98 0.56 121.6 352 2.36 341 850135582 0.47 0.99 51.64 151.62 0.3 0.26 0.27 0.01 good 0.66 73.08 0 -0.03 0.07
951765692 1.13855 80 -0.07 0.02 1.14 2.92 0.83 0.29 114.09 353 2.15 342 850135582 0.37 0.99 48.63 391.37 0.48 0.12 0.09 0 good 0.48 47.08 0 -0.06 0.09
951765697 9.08022 80 0.69 0.09 9.08 4.04 0.99 0.6 159.88 354 2.32 343 850135584 0.54 0.99 61.19 153.43 0.44 0.26 0 0 good 0.48 63.08 0 -0.1 0
951765703 3.58978 150 0.71 0.07 3.59 1.84 0.58 0.52 108.43 355 1.22 344 850135578 0.31 0.99 44.96 360.89 0.29 0.33 0.5 0 noise 0.58 35.07 0.08 -0.03 0.61
951765710 0.003 170 -1.48 nan 0 4 nan 0.76 95.93 356 1.34 345 850135584 0.25 0.23 nan 0 0.35 0.21 0.26 0 noise 1.69 3.11185e+12 nan -0.02 0
951765716 3.34756 140 0.56 0.08 3.35 2.67 0.67 0.51 96.11 357 1.55 346 850135590 0.3 0.99 47.02 324.67 0.25 0.3 0.5 0 good 0.56 39.58 0.04 -0.04 0.64
951765721 10.0994 80 -0.62 0.07 10.1 2.81 0.88 1.62 117.72 358 1.98 347 850135588 1.96 0.99 50.42 142.8 0.11 0.66 0.1 0.01 good 0.21 48.86 0.03 -0.01 0.06
951765727 15.782 140 0.37 0.1 15.78 3.97 0.93 1.51 181.62 359 3.07 348 850135588 1.1 0.99 60.27 112.92 0.09 0.76 0.01 0.01 good 1.05 56.55 0.02 -0.03 0.05
951765732 1.64645 60 -0.21 0.05 1.65 4.62 0.97 0.34 197.37 360 2.73 349 850135590 0.54 0.99 40.77 141.11 0.75 0.27 0 0 good -0.69 46.89 0.01 -0.17 0
951765737 6.97155 100 0.57 0.1 6.97 2.8 0.87 1.29 89.66 361 0.7 350 850135596 7.77 0.99 46.35 252.08 0.01 nan 0.03 0 good 2.75 50.71 0.01 nan 0.06
951765743 10.5288 110 0.86 0.04 10.53 2.1 0.3 1 58.02 362 0.32 351 850135598 1.42 0.99 75.73 626.69 0.03 nan 0.35 0.06 noise -2.02 35.64 0.11 -0.01 0.12
951765747 13.0858 130 0.87 0.01 13.09 2.04 0.34 1.18 56.22 363 0.34 352 850135598 1.44 0.99 31.45 446.75 0.01 nan 0.14 0.07 noise -1.47 37.97 0.11 -0.02 0.02
951765753 13.4251 130 -0.06 0 13.43 1.61 0.32 1.07 48.75 364 0.3 353 850135598 1.29 0.99 30.03 436.84 0.05 nan 0.09 0.11 noise -1.35 37.3 0.18 -0.02 0.05
951765758 13.2055 110 1.97 0.01 13.21 1.41 0.34 2.16 46.52 365 0.32 354 850135598 1.3 0.99 41.31 525.2 0.01 nan 0.05 0.08 noise -3.41 38.02 0.17 -0.61 0.02
951765764 19.5368 100 -0.35 0.06 19.54 4.1 0.97 1.02 58.84 366 0.33 355 850135598 1.43 0.99 31.8 348.5 0.02 nan 0.04 0.01 noise 3.84 63.32 0.02 nan 0.04
951765769 7.64943 60 0 0.13 7.65 3.92 0.97 1.36 128.07 367 0.73 356 850135598 2.81 0.99 60.32 199.26 0.07 nan 0.06 0 good 1.1 53.98 0.01 -0.01 0.11
951765775 0.31001 90 -0.41 0.04 0.31 4.1 0.68 0.62 111.08 368 1.83 357 850135602 0.29 0.86 27.56 111.46 0.35 0.19 0.32 0 noise 0.41 47.54 0 -0.05 4.84
951765780 0.00289 170 1.19 nan 0 4.64 nan 0.47 134.75 369 2.14 358 850135602 0.06 0.19 nan 0 0.49 0.21 0.46 0 noise 0 1.47191e+13 nan -0.04 0
951765786 2.58722 110 0.51 0.07 2.59 3.7 0.81 0.69 83.95 370 1.46 359 850135604 0.02 0.99 45.43 284.91 0.18 0.33 0.3 0 good 0.96 51.12 0.01 -0.01 0.27
951765793 7.54827 70 -0.34 0.07 7.55 6.74 1 0.33 210.46 371 2.55 360 850135612 0.12 0.99 52.64 78.99 0.8 0.26 0 0 good 1.37 80.65 0 -0.23 0
951765801 1.88846 80 0.21 0.05 1.89 3.46 0.66 0.67 138.63 372 1.58 361 850135606 0.16 0.99 37.74 303.18 0.54 0.22 0.46 0 good 0.62 36.46 0.06 -0.04 4.76
951765809 5.72387 130 0.18 0.06 5.72 3.89 0.93 0.19 119.03 373 1.74 362 850135602 0.23 0.99 75.95 241.1 0.49 0.15 0.5 0.01 good 0.03 48.86 0.03 -0.15 3.31
951765815 0.00713 60 -0.34 nan 0.01 5.91 nan 0.51 140.89 374 2.38 363 850135602 0.12 0.3 nan 0 0.49 0.18 0.46 0 noise 0.41 50.12 0 -0.03 0
951765820 5.49643 70 -0.69 0.1 5.5 6.31 1 0.25 233 375 3.01 364 850135610 0.12 0.99 57.86 95.94 1.07 0.19 0 0 good 0 73.48 0 -0.24 0.04
951765825 1.98983 150 0.05 0.08 1.99 2.11 0.61 0.58 65.32 376 0.95 365 850135612 0.44 0.99 115.45 645.08 0.17 1.07 0.5 0 good 1.15 30.19 0.16 -0.02 1.46
951765832 5.27602 170 0.93 0.01 5.28 1.45 0.78 1.19 32.95 377 0.71 366 850135624 0.12 0.99 42.6 568.58 0.07 0.58 0.5 0.13 noise 1.03 76.64 0.08 -0.02 1.1
951765836 1.17183 80 0.16 0.05 1.17 4.02 0.89 0.89 99.7 378 2.26 367 850135622 0.18 0.99 28.64 370.27 0.34 0.16 0.06 0.01 noise 1.37 45.85 0.05 -0.02 0.71
951765841 0.00858 150 -0.26 nan 0.01 4.76 0.5 0.52 137.58 379 1.73 368 850135614 0 0.27 2.38 0 0.39 0.23 0.5 0 noise 0.25 51.78 0 -0.02 0
951765849 1.28302 120 0.13 0.03 1.28 2.99 0.62 0.45 84.34 380 1.58 369 850135622 0.16 0.99 24.27 169.28 0.26 0.26 0.5 0.02 noise 0.22 38.21 0.11 -0.03 7.27
951765855 1.28787 110 0.15 0.05 1.29 3.15 0.65 0.77 86.98 381 1.81 370 850135628 0.37 0.99 35.92 482.31 0.26 0.23 0.5 0.02 good 1.72 38.44 0.1 -0.02 2.97
951765859 0.18828 110 0.23 0.04 0.19 3.26 0.41 0.62 87.59 382 1.91 371 850135628 0.39 0.85 25.33 136.03 0.24 0.27 0.5 0.01 noise 1.03 37.93 0.03 -0.01 8.74
951765866 3.43602 80 -0.82 0.08 3.44 3.25 0.82 0.27 85.98 383 1.64 372 850135630 0.17 0.99 53.48 306.8 0.39 0.23 0.31 0.04 good -0.14 71.39 0.07 -0.05 0.57
951765870 0.45974 70 0.48 0.06 0.46 3.05 0.81 0.6 94.19 384 1.99 373 850135636 0.69 0.99 23.73 292.94 0.29 0.21 0.47 0 noise 1.37 39.56 0.04 -0.03 5.86
951765876 0.00134 140 0.38 nan 0 2.89 nan 0.47 151.56 385 2.26 374 850135636 0.38 0.12 nan 0 0.49 0.19 0.5 0 noise 0.24 4.50625e+13 nan -0.07 0
951765881 1.33448 130 0.86 0.02 1.33 2.35 0.81 0.98 59.13 386 1.2 375 850135642 8.45 0.98 21.34 283.81 0.03 nan 0.5 0.02 good 0 48.82 0.06 nan 2
951765886 3.61417 50 -0.41 0.07 3.61 3.13 0.97 1.77 97.81 387 1.71 376 850135642 2.6 0.99 30.06 150.26 0.07 1.35 0.02 0.08 good 0.69 76.4 0.04 nan 0.03
951765892 0.73668 40 1.37 0.14 0.74 4.11 0.91 0.78 101.6 388 2.47 377 850135648 0.12 0.95 36.65 292.55 0.28 0.29 0.11 0 good 2.06 53.39 0.02 -0.01 0.86
951765898 21.7077 90 0.01 -0.01 21.71 2.49 0.94 1.4 24.14 389 0.33 378 850135690 0.47 0.99 54.46 644.79 0.01 1.55 0.5 0.06 noise 28.16 672.32 0.13 -0.01 0.3
951765904 0.91411 110 0.35 0.24 0.91 3.3 0.58 0.66 92.66 390 1.54 379 850135684 0.17 0.97 31.69 286.94 0.11 1 0 0.01 noise 0 20.57 0.14 -0.09 18.91
951765910 10.1545 100 0.32 0.11 10.15 2.04 0.87 0.66 34.58 391 0.57 380 850135690 0.17 0.99 38.31 719.8 0.05 1 0.5 0.06 noise 0 40.16 0.15 -0.01 3.04
951765913 10.8102 50 -0.34 0.01 10.81 2.4 0.52 0.49 281.45 392 3.11 381 850135072 0.38 0.99 32.7 83.33 0.9 0.22 0.01 0.02 good 0 41.89 0.04 -0.13 0.07
951765921 0.11367 80 -0.41 nan 0.11 3.22 0 0.54 206.54 393 1.81 382 850135072 0.42 0.7 14.76 48.83 0.55 0.32 0.37 0 good 0.21 23.91 0.02 -0.07 0
951765926 9.27046 70 -0.69 0.12 9.27 5.24 1 1.26 136.58 394 1.74 383 850135112 1.29 0.99 13.75 152.34 0.06 0.91 0.02 0 good 0.48 84.83 0 -0 0.04
951765931 5.00807 80 -0.69 0.07 5.01 3.88 0.83 1.25 135.64 395 1.24 384 850135118 7.23 0.99 25.1 236.37 0.04 nan 0.12 0 good -0.24 51.48 0.01 -0.01 0.14
951765944 1.90417 60 0 0.05 1.9 3.76 0.36 0.48 245.52 396 2.87 385 850135172 0.35 0.99 36.49 188.18 0.8 0.23 0 0 good 0.69 31.49 0.02 -0.16 0.15
951765950 1.62072 50 -0.69 0.04 1.62 4.09 0.32 1.35 215.39 397 1.66 386 850135174 4.38 0.99 15.78 218.98 0.16 nan 0.05 0 good 1.37 33.75 0.01 -0.02 0.09
951765955 0.16513 60 nan nan 0.17 6.15 0.89 1.59 223.68 398 2.38 387 850135324 2.03 0.89 30.02 101.26 0.02 2.62 0 0 good 1.59 47.02 0 -0.02 0
951765961 0.948 90 1.17 0.04 0.95 2.65 0.69 0.81 75.69 399 1.65 388 850135334 0.16 0.99 32.18 380.84 0.22 0.22 0.14 0.01 good 1.69 45.56 0.01 -0.03 0.86
951765966 0.10117 50 0.34 nan 0.1 2.21 0.1 0.66 122.14 400 1.66 389 850135374 0.03 0.97 23.95 78.86 0.46 0.18 0.21 0 good 0.34 25.36 0.05 -0.03 11.35
951765973 0.67416 70 0.69 0.05 0.67 3.58 0.6 0.74 115.43 401 1.77 390 850135372 0.39 0.99 47.96 420 0.42 0.14 0.07 0 good 1.72 34.58 0.09 -0.04 4.01
951765977 0.50407 80 1.03 0 0.5 3.88 0.62 0.6 63.06 402 1.21 391 850135380 0.15 0.99 49.52 637.74 0.21 0.19 0.12 0.01 good 1.51 46.33 0.01 -0.02 2.59
951765984 0.12969 160 -1.57 0.15 0.13 3.06 0.37 1.39 119.14 403 0.88 392 850135448 0.24 0.89 58.47 127.63 0.03 1.03 0.07 0 noise 2.37 16.57 0.4 -0.03 211.87
951765988 0.45085 50 -3.43 0.01 0.45 4.31 0.85 1.37 152.06 404 0.62 393 850135470 0.11 0.74 20.4 19.72 0.14 0.33 0.12 0 good -0.48 45.49 0 -0.01 0
951765995 1.32508 70 0.48 0.02 1.33 3.83 0.74 0.73 136.78 405 2.7 394 850135604 0.09 0.99 42.33 215.45 0.44 0.21 0.01 0 good 1.37 44 0.01 -0.04 0.49
951766001 0.1395 110 0.29 nan 0.14 3.13 0.77 0.59 169.88 406 2.17 395 850135684 0.16 0.92 25.78 49.92 0.25 0.78 0.01 0 noise 0 13.63 0.3 -0.16 87.57
951766007 0.57589 60 0 0.02 0.58 3.66 0.76 0.54 123.99 407 1.32 396 850135330 0.1 0.99 21.32 269.27 0.24 0.26 0.03 0 good 0.76 47.54 0 -0.03 0.23
951766012 0.09083 50 -0.96 -0.12 0.09 4.32 0 1.11 312.1 408 1.33 397 850135474 0.2 0.52 6.35 11.14 0.3 0.36 0.08 0 good -2.75 18.14 0.02 -0.01 0
951766019 0.02501 40 0 nan 0.03 10.73 0.76 0.66 494.69 409 5.05 398 850135372 0.21 0.6 nan 0 1.98 0.12 0.04 0 good 0 86.41 0 -0.17 0
951766024 0.00837 30 0.69 nan 0.01 6.81 0 0.58 607.06 410 7.22 399 850135372 0.21 0.41 nan 0 2.14 0.1 0 0 good 0.69 86.57 0 -0.16 0
951766138 3.56684 30 nan nan 3.57 2.03 0.5 0.56 46.73 0 1.68 0 850137692 0.75 0.99 22.36 402.05 0.27 0.27 0.5 0.01 good 0.69 21.36 0.05 -0.04 0.05
951766144 10.9933 30 nan 0.09 10.99 5.03 0.94 0.49 170.97 1 4.11 1 850137694 0.73 0.99 9.47 141.83 0.52 0.4 0 0.01 good 1.03 69.52 0.01 -0.11 0
951766152 7.44338 30 nan 0.07 7.44 2.72 0.8 0.56 97.33 2 2.47 2 850137694 0.61 0.99 13.98 293.31 0.27 0.25 0.5 0.01 good 0 43.3 0.01 -0.05 0.23
951766160 4.75634 40 nan 0.1 4.76 2.63 0.71 0.54 108.12 3 2.6 3 850137694 0.52 0.99 35.05 247.18 0.31 0.22 0.07 0.01 good 0.82 31.66 0.02 -0.04 0.16
951766167 10.7141 30 nan 0.24 10.71 4.63 0.99 0.54 120.07 4 2.76 4 850137696 0.53 0.99 10.94 253.75 0.32 0.25 0.01 0 good 0.69 95.02 0 -0.04 0.02
951766173 9.36047 30 nan 0.36 9.36 6.64 1 0.54 266.39 5 5.07 5 850137696 0.46 0.99 18.53 56.64 0.87 0.23 0 0 good 0.34 80.08 0 -0.12 0
951766180 10.412 40 nan 0.18 10.41 5.04 1 0.58 162.85 6 3.28 6 850137692 0.49 0.99 13.94 93.89 0.67 0.18 0 0 good -0.41 90.48 0 -0.1 0.01
951766188 5.87175 60 -0.69 0.12 5.87 1.96 0.86 0.58 96.41 7 2.41 7 850137698 0.58 0.99 20.3 264.18 0.24 0.27 0.5 0.01 good 0.55 40.56 0.01 -0.04 0.13
951766195 8.16663 40 nan 0.08 8.17 3.18 0.95 0.56 122.78 8 2.7 8 850137696 0.52 0.99 14.95 182.92 0.36 0.22 0 0 good 0 62.59 0 -0.05 0.11
951766203 1.90221 50 -0.34 0.51 1.9 6.8 0.98 0.52 227.15 9 5.32 9 850137702 0.71 0.99 17.68 67.62 0.7 0.43 0 0 good 0.69 80.87 0 -0.15 0
951766208 12.5293 60 -0.34 0.13 12.53 3.63 0.97 0.56 90.46 10 2.7 10 850137702 0.51 0.99 21.4 191.77 0.24 0.25 0.08 0 good 0.21 61.47 0.01 -0.05 0.22
951766214 0.0589 60 0 nan 0.06 5.75 0 0.55 172.69 11 3.83 11 850137702 0.87 0.55 17.26 23.89 0.51 0.67 0.09 0 noise 0.48 34.46 0 -0.1 11.16
951766220 0.17577 60 nan nan 0.18 2.4 0 0.59 76.38 12 1.41 12 850137696 0.8 0.99 37.98 194.45 0.18 0.34 0.3 0 good 0.37 28.48 0.02 -0.03 0
951766225 5.32087 50 0.69 0.42 5.32 6.1 1 0.55 168.69 13 3.98 13 850137700 0.71 0.99 33.84 69.2 0.48 0.33 0 0 good 0.41 61.97 0 -0.1 0
951766229 4.65135 60 -0.34 0.31 4.65 6.3 0.97 0.52 125.53 14 3.9 14 850137704 0.41 0.99 14.89 89.04 0.4 0.18 0 0 good 0.48 88.58 0 -0.06 0.04
951766235 0.96609 60 -2.06 0.21 0.97 6.33 0.99 0.55 56.42 15 1.71 15 850137704 3.26 0.76 50.53 593.52 0.21 0.21 0.5 0 good 0.41 113.93 0 -0.01 0
951766240 5.05385 80 0 0.1 5.05 2.98 0.74 0.58 69.18 16 2.12 16 850137702 0.54 0.99 19.23 196 0.18 0.26 0.38 0 good 1.47 51.45 0.01 -0.04 0.1
951766245 3.38342 70 0 0.19 3.38 7.22 0.97 0.58 130.8 17 3.98 17 850137706 0.39 0.99 21.13 85.17 0.4 0.19 0 0 good 0.55 74.94 0 -0.06 0.03
951766251 6.44888 80 0 0.11 6.45 2.89 0.88 0.6 64.94 18 2.3 18 850137706 0.47 0.99 18.91 203.71 0.14 0.34 0.5 0.01 good -0.55 57.77 0.01 -0.03 0.07
951766256 0.70733 80 -0.21 0.04 0.71 2.75 0.28 0.54 48.97 19 1.6 19 850137706 0.42 0.99 30.38 616.5 0.14 0.23 0.33 0 good 0 36.52 0.01 -0.03 0.08
951766262 6.33583 80 -0.27 0.09 6.34 4.65 0.92 0.47 89.61 20 2.99 20 850137710 0.65 0.99 21.62 101.34 0.28 0.27 0 0 good 0.41 57.29 0.01 -0.05 0.05
951766266 8.58318 80 0.14 0.15 8.58 4.64 0.88 0.59 74.93 21 2.61 21 850137710 0.55 0.99 17.37 130.59 0.2 0.25 0.09 0 good 0.62 69.35 0 -0.03 0.09
951766271 6.02665 90 -0.34 0.05 6.03 3.36 0.85 0.59 65.11 22 2.3 22 850137710 0.58 0.99 17.03 146.86 0.18 0.25 0.5 0 good 0.96 56.91 0.01 -0.04 0.17
951766276 2.62132 90 -0.34 0.15 2.62 3.57 0.76 0.66 62.41 23 1.7 23 850137712 0.74 0.99 21.51 385.77 0.12 0.34 0.5 0 good -0.34 52.6 0 -0.03 0.12
951766280 4.53841 70 -1.24 0.13 4.54 3.43 0.95 0.67 109.6 24 2.72 24 850137712 0.51 0.99 27.75 122.79 0.31 0.27 0.02 0 good 0.41 61.25 0 -0.05 0.07
951766286 6.32157 50 -1.37 0.21 6.32 4.1 0.98 0.59 172.64 25 3.88 25 850137712 0.5 0.99 20.87 39.08 0.49 0.23 0 0 good 1.03 88.39 0 -0.07 0
951766291 2.9985 70 -0.69 0.11 3 2.97 0.74 0.59 73.1 26 2.27 26 850137712 0.55 0.99 33.54 270.2 0.2 0.22 0.21 0 good 0.14 55.24 0 -0.03 0.03
951766298 8.71307 80 0 0.16 8.71 4.07 0.99 0.55 90.75 27 2.61 27 850137714 0.48 0.99 19.79 119.99 0.25 0.3 0 0 good 1.1 94.31 0 -0.04 0.03
951766303 9.10947 60 -0.62 0.16 9.11 4.16 0.98 0.66 146.33 28 3.85 28 850137716 0.63 0.93 25.55 129.01 0.38 0.27 0.02 0 good 0.34 84.8 0 -0.06 0.05
951766309 27.6031 50 -1.72 0.07 27.6 5.72 1 0.84 132.06 29 2.54 29 850137718 0.35 0.99 8.98 49.88 0.25 0.34 0 0 good 0.69 117.47 0 -0.02 0
951766314 13.9623 80 -0.48 0.08 13.96 4.4 0.99 0.65 133.62 30 3.22 30 850137718 0.58 0.99 15.56 74.63 0.25 0.34 0.01 0 good 0.89 101.42 0 -0.08 0.02
951766322 13.2362 70 -0.69 0.19 13.24 6.17 1 0.62 171.41 32 4.1 31 850137718 0.51 0.99 26.18 58.06 0.39 0.29 0 0 good 1.3 113.45 0 -0.09 0.01
951766327 20.8808 50 -0.69 0.17 20.88 3.34 0.98 0.62 77.33 33 2 32 850137720 0.21 0.99 6.15 59.93 0.23 0.22 0.37 0.01 good 0.69 117.81 0 -0 0.03
951766334 9.46226 80 -0.34 0.18 9.46 5.24 0.98 0.59 161.36 34 4.05 33 850137716 0.56 0.99 33.4 71.71 0.43 0.27 0 0 good 1.37 69.3 0 -0.08 0.01
951766340 3.49089 60 -0.21 0.15 3.49 3.38 0.75 0.62 154.86 35 3.83 34 850137720 0.58 0.99 13.15 79.16 0.38 0.3 0.07 0 good 1.03 35.08 0.03 -0.07 0.18
951766346 7.1218 70 -0.34 0.05 7.12 2.46 0.76 0.65 88.55 36 2.31 35 850137720 0.48 0.99 25.61 131.8 0.23 0.27 0.22 0.01 good 1.03 50.06 0.01 -0.03 1.47
951766353 0.01281 110 -0.82 nan 0.01 3.36 nan 0.65 96.83 37 2.11 36 850137720 0.47 0.64 nan 0 0.26 0.25 0.5 0 good 2.64 22.17 0.01 -0.04 235.9
951766360 0.39991 70 0.34 nan 0.4 4.26 0.77 0.73 73.85 39 1.65 37 850137722 0.52 0.99 17.89 134.98 0.21 0.23 0.06 0 good 0.96 53.08 0 -0.03 0
951766366 10.6936 80 -0.07 0.25 10.69 5.83 0.99 0.51 129.08 40 3.32 38 850137724 0.59 0.99 12.04 65.88 0.36 0.25 0 0 good 0.89 131.18 0 -0.07 0.01
951766372 12.1386 50 0 0.23 12.14 7.38 1 0.51 150.6 41 3.82 39 850137724 0.42 0.99 25.28 67.62 0.49 0.19 0 0 good 0.69 136.63 0 -0.07 0
951766379 6.03647 90 0.21 0.19 6.04 3.63 0.79 0.58 71.67 42 1.86 40 850137726 0.73 0.99 26.53 233.62 0.17 0.41 0.5 0.01 good 0.27 55.71 0.01 -0.04 0.09
951766385 3.86827 80 0.34 0.07 3.87 3.88 0.8 0.63 87.87 43 2.16 41 850137726 0.47 0.99 6.26 160.72 0.23 0.25 0.5 0 good 0.82 53.68 0 -0.04 0.16
951766390 6.73223 60 -1.37 0.05 6.73 4.27 0.85 0.62 99.84 44 2.53 42 850137726 0.56 0.99 14.55 109.37 0.25 0.29 0.07 0 good 0.21 58.86 0.01 -0.05 0.12
951766398 1.86687 110 0.1 0.1 1.87 3.06 0.85 0.63 78.99 45 1.61 43 850137736 0.82 0.99 26.2 490.9 0.15 0.49 0.5 0 good 0.27 45.64 0.01 -0.03 0.12
951766403 7.8248 60 -0.89 0.47 7.82 11.13 1 0.55 420.91 46 7.63 44 850137730 0.47 0.99 19.52 66.03 1.25 0.21 0 0 good -0.34 234 0 -0.21 0
951766408 10.6266 50 -0.69 0.41 10.63 9.28 1 0.58 300.06 48 5.54 45 850137730 0.48 0.99 19.09 53.34 0.88 0.23 0 0 good 1.03 266.88 0 -0.13 0
951766416 10.091 70 -0.96 0.18 10.09 4.98 1 0.55 125.05 49 2.71 46 850137732 0.52 0.99 11.74 85.28 0.36 0.26 0 0 good 0.96 123.05 0 -0.07 0.02
951766421 0.68915 80 -0.76 nan 0.69 2.02 0.32 0.69 89.76 50 2 47 850137738 0.64 0.99 16.68 464.42 0.18 0.34 0.43 0 good 0.07 26.84 0.03 -0.03 0
951766427 7.16882 70 -0.69 0.17 7.17 4.43 0.96 0.59 126.46 51 3.07 48 850137734 0.55 0.99 8.77 64.23 0.34 0.23 0.07 0 good 0.96 70.52 0 -0.06 0.13
951766432 7.59136 60 -0.96 0.09 7.59 4.76 0.97 0.55 81.34 52 2.01 49 850137734 0.65 0.99 7.24 100.38 0.21 0.25 0.11 0 good 0.34 82.32 0 -0.04 0.07
951766438 5.55885 70 -0.69 0.08 5.56 2.34 0.95 0.66 92.48 53 2.25 50 850137736 0.5 0.99 24.29 173.23 0.22 0.25 0.26 0 good 0.48 67.77 0 -0.04 0.04
951766442 9.71284 50 -0.69 0.4 9.71 10.52 1 0.52 309.92 54 7.01 51 850137736 0.61 0.99 12.48 28.22 0.91 0.23 0 0 good 0.34 190.44 0 -0.19 0
951766447 13.6457 70 -1.37 0.17 13.65 4.21 0.98 0.6 110.59 55 2.39 52 850137738 0.66 0.99 17.02 107.45 0.29 0.37 0.02 0 good 0.48 79.45 0 -0.05 0.05
951766452 5.53095 50 -0.34 0.43 5.53 10.15 1 0.54 305.81 56 6.16 53 850137738 0.48 0.99 11.67 37.22 0.99 0.19 0 0 good 0.34 186.94 0 -0.17 0
951766458 15.2865 60 -1.44 0.31 15.29 7.25 1 0.62 216.51 57 5.28 54 850137742 0.47 0.99 16.79 38.87 0.52 0.26 0 0 good 0.69 100.72 0 -0.09 0
951766463 8.09647 60 -0.21 0.18 8.1 5.1 0.99 0.56 148.06 58 3.49 55 850137742 0.42 0.99 17.82 89.98 0.44 0.21 0 0 good 0.69 93.12 0 -0.06 0.02
951766469 0.06086 100 0.34 nan 0.06 3.01 0 0.62 69.27 59 1.39 56 850137742 0.73 0.95 17.86 14.07 0.14 0.33 0.5 0 good -0.26 30.71 0 -0.03 0
951766474 15.4068 60 -0.34 0.13 15.41 4.07 0.99 0.62 107.21 60 2.45 57 850137742 0.54 0.99 17.06 87.03 0.27 0.25 0 0 good 0.21 98.15 0 -0.05 0.01
951766480 6.592 60 -0.55 0.44 6.59 8.65 1 0.65 273.02 61 6.85 58 850137744 0.44 0.99 26.88 56.41 0.8 0.21 0 0 good 0.34 180.65 0 -0.1 0
951766485 1.00887 90 -0.62 0.09 1.01 3.14 0.7 0.58 81.33 62 2.12 59 850137744 0.59 0.99 23.85 399.27 0.19 0.32 0.05 0 good -0.27 55.26 0 -0.02 0.11
951766489 5.3901 90 0 0.13 5.39 3.27 0.56 0.69 70.57 63 2.21 60 850137748 0.65 0.99 20.71 209.9 0.12 0.34 0.5 0.01 good 0.31 39.55 0.02 -0.03 0.07
951766494 5.21226 60 0 0.23 5.21 4.64 0.95 0.58 102.87 64 3.15 61 850137750 0.46 0.99 15.82 131.16 0.32 0.19 0.02 0 good 0.21 55.38 0 -0.04 0.06
951766500 0.344 80 0.07 0.1 0.34 3.21 0.17 0.67 76.39 65 2.49 62 850137750 0.51 0.99 16.77 385.37 0.2 0.26 0.02 0 good 0.07 37.14 0 -0.03 0
951766504 7.791 100 -0.96 0.05 7.79 3.78 0.91 0.58 67.44 66 2.3 63 850137752 0.58 0.99 14.92 130.82 0.18 0.26 0.45 0 good -0.21 60.75 0.01 -0.03 0.11
951766510 3.71916 50 -0.34 0.45 3.72 10.24 0.98 0.56 268.67 67 6.89 64 850137752 0.58 0.99 4.06 22.75 0.77 0.21 0 0 good 0 113.81 0 -0.16 0
951766515 14.5508 80 -1.33 0.04 14.55 3.66 0.91 0.6 65.48 68 2.16 65 850137752 0.5 0.99 13.43 106.95 0.17 0.23 0.23 0 good 0 89.52 0.01 -0.03 0.05
951766521 10.2152 70 -1.24 0.11 10.22 4.05 0.96 0.6 90.53 69 2.88 66 850137750 0.57 0.99 14.51 84.59 0.24 0.26 0 0 good -0.21 68.26 0 -0.05 0.03
951766526 7.57307 60 0 0.13 7.57 5.39 1 0.65 79.8 70 2.6 67 850137754 0.53 0.99 13.43 118.83 0.22 0.33 0 0 good 1.03 81.69 0 -0.04 0.02
951766531 8.37578 40 -0.69 0.12 8.38 5.57 0.99 0.59 112.54 71 3.34 68 850137754 0.34 0.99 18.79 71.86 0.34 0.19 0 0 good -0.69 92.19 0 -0.04 0.01
951766541 15.5747 80 -0.48 0.17 15.57 4.09 0.99 0.63 78.81 72 2.65 69 850137756 0.48 0.99 11.86 73.16 0.2 0.26 0 0 good 0.69 82.31 0 -0.03 0.04
951766546 12.2331 60 -0.21 0.21 12.23 5.71 0.99 0.54 114.12 73 3.7 70 850137758 0.37 0.99 11.29 49.82 0.36 0.19 0 0 good 0.69 96.17 0 -0.04 0.01
951766552 6.38915 60 -0.62 0.13 6.39 3.46 0.73 0.63 90.08 74 2.78 71 850137758 0.48 0.99 15.81 107.82 0.22 0.26 0.05 0.01 good 0 45.11 0.02 -0.04 0.13
951766557 4.74549 40 -1.37 0.18 4.75 4.96 0.99 0.65 126.56 75 3.6 72 850137758 0.4 0.99 10.73 66.86 0.38 0.21 0 0 good 0 62.55 0 -0.05 0.03
951766562 0.16058 60 -0.34 0.03 0.16 2.47 0.04 0.65 62.15 76 1.89 73 850137758 0.47 0.99 22.42 176.92 0.14 0.32 0.01 0 good 1.37 31.84 0.01 -0.04 0
951766567 1.90572 40 -0.34 0.04 1.91 3.85 0.6 0.71 83.57 77 2.68 74 850137758 0.31 0.99 6.65 155.24 0.28 0.21 0.09 0 good 0 42.35 0.01 -0.03 0.2
951766573 14.5612 30 0 0.14 14.56 6.05 1 0.66 61.2 78 2.29 75 850137760 0.69 0.99 6.47 93.27 0.12 0.33 0.04 0 good nan 114.07 0 -0.03 0
951766577 2.15807 130 -0.12 0.07 2.16 2.61 0.53 0.67 64.76 79 2.3 76 850137766 0.68 0.99 13.39 323.27 0.12 0.37 0.5 0 good -0.12 37.77 0.02 -0.03 0.08
951766582 6.21069 100 -0.62 0.08 6.21 3.44 0.92 0.55 58.71 80 2.28 77 850137766 0.57 0.99 11.56 173.82 0.16 0.27 0.4 0.01 good -0.31 66.41 0 -0.03 0.03
951766589 13.1292 60 -2.06 0.1 13.13 3.88 0.97 0.73 64.86 81 2.32 78 850137766 0.37 0.99 9.61 136.16 0.17 0.23 0.45 0 good 1.3 76.83 0 -0.02 0.01
951766593 2.40938 70 0.21 0.03 2.41 3.44 0.63 0.69 71 82 2.55 79 850137766 0.43 0.99 17.62 235.97 0.2 0.22 0.5 0 good 1.03 44.38 0.01 -0.02 0.29
951766599 10.8013 60 -10.3 0.09 10.8 4.81 0.96 0.67 59.96 83 2.1 80 850137766 0.59 0.99 18 142.36 0.12 0.27 0.02 0 good 1.3 70.82 0 -0.03 0.01
951766605 0.91628 10 nan nan 0.92 7.49 1 0.25 85.29 84 3.1 81 850137768 0.25 0.91 17.69 216.72 0.35 0.12 0.42 0 noise nan 91.39 0 -0.07 0
951766611 8.05554 70 -0.96 0.35 8.06 9.22 1 0.54 182.48 85 5.94 82 850137770 0.44 0.99 11.54 35.32 0.54 0.19 0 0 good -0.21 153.7 0 -0.08 0
951766616 4.09551 60 -0.34 0.13 4.1 4.32 0.93 0.58 74.61 86 2.63 83 850137774 0.42 0.99 5.38 158.57 0.22 0.21 0.4 0 good 0.21 66.47 0 -0.03 0.12
951766621 4.53768 50 -0.69 0.32 4.54 8.81 1 0.58 166.78 88 4.84 84 850137776 0.55 0.99 17.32 73.02 0.47 0.21 0 0 good 0.34 128.98 0 -0.1 0.01
951766625 7.22948 70 -1.3 0.22 7.23 5.75 0.97 0.55 117.41 89 3.47 85 850137778 0.51 0.97 9.33 134.41 0.4 0.16 0 0 good 0.07 74.16 0 -0.06 0
951766630 17.7724 80 -0.82 0.1 17.77 2.87 0.96 0.62 69.77 90 2.14 86 850137778 0.49 0.99 9.75 103.38 0.18 0.25 0.02 0.01 good 0.76 71.77 0.01 -0.03 0.07
951766634 5.82938 60 -0.07 0.18 5.83 6.66 1 0.59 91.38 91 2.63 87 850137780 0.34 0.99 18.31 126.77 0.29 0.19 0 0 good 0.34 104.45 0 -0.03 0.02
951766636 10.1654 50 -0.34 0.08 10.17 2.95 0.93 0.52 120.67 92 3.67 88 850137780 0.44 0.99 16.95 64.28 0.37 0.19 0 0 good 0.34 50.85 0.03 -0.06 0.07
951766640 14.9032 80 -0.62 0.08 14.9 2.87 0.93 0.56 87.19 93 2.62 89 850137782 0.67 0.99 14.4 93.83 0.22 0.29 0.06 0.01 good 0.07 68.56 0.01 -0.04 0.03
951766645 9.48799 60 -0.21 0.21 9.49 9.1 1 0.51 214.75 94 5.57 90 850137782 0.63 0.99 17.09 57.75 0.68 0.18 0 0 good 0.34 116.17 0 -0.13 0
951766650 9.78735 70 -1.1 0.06 9.79 4.2 0.89 0.66 74.19 95 2.3 91 850137782 0.75 0.99 17.37 122.98 0.17 0.34 0.1 0.01 good 1.72 59.97 0.01 -0.04 0.03
951766657 4.37906 100 -1.37 0.1 4.38 3.99 0.98 0.73 45.32 96 1.29 92 850137784 0.57 0.99 20.51 287.44 0.07 0.33 0.26 0 good -0.14 76.53 0 -0.02 0.04
951766662 8.9896 80 -1.1 0.13 8.99 5.49 0.99 0.58 96.68 97 3.17 93 850137784 0.59 0.99 8.63 85.07 0.25 0.25 0 0 good -0.41 89.07 0 -0.05 0.02
951766673 19.209 70 -0.69 0.17 19.21 4.81 0.98 0.56 99.11 98 3.46 94 850137786 0.47 0.99 10.99 59.82 0.27 0.25 0 0 good 0.21 104.45 0 -0.05 0.01
951766679 4.43683 60 -0.34 0.14 4.44 7.35 0.99 0.45 115.29 99 3.56 95 850137786 0.36 0.99 13.39 117.16 0.44 0.15 0 0 good 0 72.19 0 -0.07 0.01
951766685 5.74878 80 -0.41 0.11 5.75 3.34 0.86 0.66 66.76 100 2.27 96 850137790 0.31 0.99 13.44 169.48 0.18 0.26 0.5 0 good 0.69 53.89 0.01 -0.03 0.16
951766691 0.12307 90 0.07 nan 0.12 3.01 0 0.65 82.51 101 2.57 97 850137792 0.53 0.99 14.96 48.16 0.22 0.23 0.11 0 good 0.34 27.46 0.01 -0.02 0
951766697 9.43415 30 -2.75 0.17 9.43 6.61 1 0.29 81.2 102 2.81 98 850137792 2.81 0.99 19.14 493.28 0.37 0.16 0.39 0 good 2.75 120.79 0 -0.05 0.06
951766704 14.0932 80 -0.41 0.22 14.09 4.61 0.97 0.58 78.81 103 2.59 99 850137792 0.59 0.99 22.22 145.49 0.21 0.26 0 0 good -0.62 77.42 0 -0.03 0.04
951766709 3.67142 90 -0.27 0.05 3.67 2.09 0.65 0.56 71.9 104 2.2 100 850137800 0.66 0.99 14.41 185.72 0.18 0.22 0.01 0.01 good 0 50.62 0.01 -0.03 0.03
951766714 5.80851 70 -1.37 0.09 5.81 2.25 0.72 0.6 60.05 105 2.12 101 850137796 0.48 0.99 15.09 173.81 0.15 0.25 0.45 0.01 good 0.41 46.76 0.02 -0.02 0.3
951766722 4.83012 90 -0.55 0.11 4.83 3.82 0.83 0.62 71.21 106 2.4 102 850137798 0.44 0.99 13.41 216.53 0.17 0.27 0.5 0 good 0 50.14 0.01 -0.02 0.18
951766727 7.53411 30 0 0.12 7.53 6.39 0.98 0.3 79.46 107 2.71 103 850137798 0.18 0.99 10.35 195.46 0.31 0.1 0.26 0 noise 0 92.3 0 -0.04 0.02
951766732 9.49439 90 0.41 0.08 9.49 4.43 0.93 0.62 67.39 108 2.37 104 850137798 0.54 0.99 17.69 148.29 0.16 0.29 0.31 0.01 good 1.03 71.09 0.01 -0.03 0.11
951766738 0.03865 90 -0.27 nan 0.04 3.32 0 0.67 83.72 109 2.29 105 850137800 0.55 0.96 nan 0 0.2 0.25 0.14 0 good 0.53 28.81 0 -0.02 0
951766743 6.11428 80 -0.82 0.07 6.11 2.52 0.83 0.69 80.89 110 2.66 106 850137800 0.59 0.99 21.3 138.53 0.21 0.25 0.06 0.01 good 0.27 45.97 0.02 -0.03 0.14
951766749 10.5625 70 -1.58 0.07 10.56 4.72 0.84 0.63 108.18 111 3.74 107 850137802 0.59 0.99 13.88 76.35 0.25 0.27 0 0.01 good 0 63.91 0.01 -0.05 0.07
951766754 4.75293 60 -1.1 0.07 4.75 2.94 0.75 0.58 64.23 112 2.16 108 850137804 0.53 0.99 14.74 164.96 0.17 0.25 0.19 0.01 good 0 51.81 0.01 -0.03 0.09
951766761 2.22317 70 -1.24 0.03 2.22 3.09 0.14 0.62 73.65 113 2.3 109 850137804 0.59 0.96 13.22 184.8 0.18 0.32 0.02 0.01 noise 0 29.6 0.04 -0.03 0.2
951766767 6.77501 50 0 0.29 6.78 9.82 1 0.63 152.2 114 4.42 110 850137804 0.42 0.99 16.21 71.41 0.4 0.21 0 0 good 0.69 146.46 0 -0.07 0
951766773 5.93778 80 -0.41 0.11 5.94 4.33 0.93 0.67 72.18 115 2.42 111 850137806 0.56 0.99 10.86 182.19 0.17 0.27 0.5 0 good 0.34 54.44 0.01 -0.04 0.23
951766780 9.65053 10 nan 0.16 9.65 6.48 1 0.44 77.73 116 2.58 112 850137808 4.42 0.95 47.72 553.86 0.31 0.15 0.37 0 noise nan 117.58 0 -0.02 0.23
951766785 0.00289 160 -1.72 nan 0 3.08 nan 0.59 69.67 117 2.11 113 850137806 0.62 0.2 nan 0 0.16 0.27 0.01 0 noise 0.33 6.23532e+12 nan -0.04 0
951766791 12.2685 60 -0.41 0.14 12.27 5.2 0.96 0.55 92.13 118 3.19 114 850137810 0.43 0.99 13.88 92.58 0.33 0.15 0 0 good 0.34 73.4 0 -0.05 0.02
951766797 9.73103 70 -0.21 0.07 9.73 3.49 0.94 0.6 76.27 119 2.76 115 850137810 0.53 0.99 11.64 87.79 0.19 0.26 0.02 0 good 0.27 59.34 0.01 -0.03 0.08
951766803 1.74886 60 0 0.19 1.75 6.51 0.93 0.8 100.55 120 3.43 116 850137810 0.31 0.99 14.63 123.63 0.34 0.16 0 0 good 0.76 66.31 0 -0.03 0.03
951766809 5.3809 60 -1.1 0.12 5.38 4.68 0.94 0.6 78.69 121 2.47 117 850137812 0.35 0.99 12.06 109.76 0.22 0.21 0 0 good 1.03 58.75 0 -0.03 0.05
951766816 13.8656 70 -1.03 0.26 13.87 7.92 0.99 0.62 121.23 122 3.96 118 850137808 0.63 0.99 17.69 67.26 0.31 0.3 0 0 good -0.14 126.25 0 -0.06 0
951766820 4.09675 30 -4.12 0.14 4.1 6.15 0.99 0.4 60.2 123 2.04 119 850137814 3.01 0.8 37.69 548 0.23 0.22 0.48 0 noise 4.81 97.66 0 -0.03 0.13
951766828 3.99424 80 -0.55 0.14 3.99 3.61 0.92 0.67 64.62 124 2.23 120 850137814 0.63 0.99 10.05 191.69 0.14 0.3 0.5 0 good 0.41 59.31 0 -0.03 0.09
951766833 3.1071 80 -1.51 0.13 3.11 2.97 0.74 0.67 57.89 125 1.63 121 850137816 0.63 0.99 22.16 381.98 0.1 0.38 0.5 0 good -0.07 47.07 0.01 -0.02 0.16
951766840 0.74164 80 -0.69 0.04 0.74 3.46 0.39 0.58 71.28 126 2.15 122 850137816 0.63 0.99 16.01 431.54 0.18 0.34 0.35 0 good -1.03 39.2 0.01 -0.03 0
951766846 3.07569 50 -0.69 0.1 3.08 4.09 0.93 0.71 134.66 127 3.46 123 850137816 0.43 0.99 7.89 94.91 0.39 0.19 0.01 0 good 0 57.55 0 -0.05 0.19
951766853 0.11636 80 0.21 nan 0.12 2.03 0 0.65 74.31 128 2.15 124 850137818 0.54 0.97 18.15 81.51 0.2 0.26 0.36 0 good 0.69 28.22 0.01 -0.04 0
951766860 0.19882 70 -0.69 nan 0.2 2.19 0.03 0.65 71 129 2.22 125 850137818 0.48 0.99 21.2 189.71 0.19 0.26 0.5 0 good 0.41 27.76 0.01 -0.04 0
951766867 5.40002 60 0.07 0.28 5.4 9.16 1 0.56 127.61 130 3.41 126 850137816 0.55 0.99 24.79 76.23 0.36 0.19 0 0 good 0.69 144.35 0 -0.08 0
951766873 6.75093 60 -0.27 0.1 6.75 4.14 0.97 0.59 114.57 131 3.19 127 850137820 0.55 0.99 15.84 87.3 0.34 0.3 0 0 good 1.03 83.19 0 -0.04 0.14
951766879 10.7436 50 -0.34 0.21 10.74 8.06 1 0.55 218.88 132 6.75 128 850137820 0.56 0.99 21.64 43.83 0.64 0.21 0 0 good 0.34 151.37 0 -0.12 0
951766886 1.85229 100 -1.65 0.12 1.85 2.46 0.82 0.58 66.87 133 1.91 129 850137820 0.62 0.99 15.18 419.64 0.17 0.3 0.5 0 good 0.14 52.56 0 -0.03 0.43
951766893 6.92133 70 -1.87 0.15 6.92 6.21 0.97 0.55 92.13 134 3.18 130 850137822 0.55 0.99 26.14 89.95 0.25 0.25 0 0 good 0.69 78.41 0 -0.04 0.01
951766899 6.3007 40 -0.69 0.21 6.3 4.7 0.89 0.58 76.1 135 2.56 131 850137822 0.54 0.99 10.6 98.06 0.22 0.26 0.03 0 good 0 54.29 0.01 -0.04 0.04
951766906 4.72048 80 -0.55 0.08 4.72 3.04 0.92 0.65 65.44 136 2.4 132 850137822 0.43 0.99 14.77 203.9 0.17 0.25 0.49 0 good -0.27 58.07 0 -0.03 0.18
951766912 6.60729 60 -0.48 0.23 6.61 6.93 0.99 0.56 145.44 137 4.56 133 850137824 0.55 0.99 15.74 62.76 0.43 0.21 0 0 good -0.69 134.58 0 -0.08 0.02
951766918 0.34101 60 -0.14 -0 0.34 4.15 0.4 0.49 90.09 138 1.46 134 850137824 0.55 0.99 24.56 367.9 0.14 0.21 0.39 0 good 0.69 49.48 0 -0.02 0.33
951766923 1.02189 60 -0.48 0.03 1.02 3.31 0.89 0.54 60.43 139 1.78 135 850137824 0.73 0.99 15.89 321.39 0.16 0.25 0.5 0 good 1.37 54.58 0 -0.03 1.26
951766928 1.23497 50 -0.34 0.25 1.23 6.54 0.96 0.59 84.58 140 2.92 136 850137828 0.44 0.99 15.54 184.5 0.26 0.22 0 0 good -1.03 66.37 0 -0.04 0.13
951766933 0.08133 90 -0.45 nan 0.08 2.36 0 0.62 57.49 141 2.1 137 850137828 0.55 0.96 11.24 4.32 0.13 0.34 0.5 0 good 0.48 30.34 0.01 -0.03 0
951766938 6.78389 60 -0.69 0.17 6.78 4.85 0.97 0.52 61.91 142 2.21 138 850137828 0.31 0.99 11.77 116.35 0.21 0.19 0.03 0 good 0.41 81.61 0 -0.02 0.31
951766942 7.80795 60 -0.27 0.21 7.81 4.83 0.98 0.55 97.58 143 3.61 139 850137830 0.58 0.99 9.06 63.78 0.28 0.22 0 0 good 0.34 76.09 0 -0.05 0.03
951766948 6.11903 50 0.34 0.16 6.12 3.86 0.87 0.59 67.22 144 2.6 140 850137830 0.44 0.99 7.77 131.27 0.2 0.22 0.5 0 good 0.69 53.67 0.01 -0.02 0.3
951766952 13.0386 70 -0.55 0.07 13.04 3.62 0.96 0.59 68.4 145 2.72 141 850137830 0.54 0.99 20.79 96.76 0.18 0.23 0.24 0.01 good 0.34 76.51 0.01 -0.03 0.08
951766957 1.97123 50 -1.1 0.07 1.97 5.39 0.91 0.59 78.65 146 2.81 142 850137832 0.55 0.99 24.39 116.25 0.23 0.23 0 0 good 1.37 51.69 0 -0.04 0.2
951766960 1.76363 70 -0.21 0.06 1.76 3.67 0.75 0.66 72.25 147 2.71 143 850137832 0.58 0.99 11.61 243.64 0.22 0.19 0.5 0 good 1.72 45.33 0.01 -0.04 0.44
951766965 6.69885 60 -0.41 0.12 6.7 3.46 0.97 0.56 65.91 148 2.63 144 850137834 0.53 0.99 11.17 111.75 0.19 0.22 0.07 0 good -0.34 70.15 0 -0.04 0.1
951766968 1.38088 50 -0.21 0.23 1.38 6.88 0.97 0.66 96.42 149 3.69 145 850137836 0.49 0.99 8.37 95.5 0.28 0.22 0 0 good 0.69 92.99 0 -0.05 0.06
951766973 0.0062 50 -0.41 nan 0.01 4.39 nan 0.54 143.32 150 3.39 146 850137838 0.57 0.4 nan 0 0.37 0.26 0.26 0 good 1.37 40.29 0 -0.06 0
951766978 4.07247 100 0.02 0.09 4.07 2.6 0.84 0.62 49.41 151 1.99 147 850137838 0.59 0.99 10.17 260.34 0.11 0.36 0.5 0 noise 0.48 50.42 0.01 -0.03 0.13
951766983 0.16131 40 0 nan 0.16 3.54 0.23 0.62 59.44 152 2.22 148 850137838 0.49 0.95 18.36 170.71 0.16 0.23 0.16 0 good 2.06 35.98 0 -0.03 0
951766990 12.6832 70 -0.12 0.14 12.68 4.59 0.98 0.59 74.67 153 2.99 149 850137838 0.52 0.99 17.36 114.2 0.2 0.26 0.01 0 good 1.37 73.62 0 -0.03 0.04
951766995 1.32249 30 0 0.21 1.32 7.91 0.99 0.45 120.73 154 3.47 150 850137838 0.3 0.99 8.79 151.88 0.49 0.15 0 0 good nan 71.79 0 -0.05 0.22
951767001 2.79089 60 0.34 0.16 2.79 4.45 0.94 0.52 64.11 155 2.45 151 850137840 0.48 0.99 15.4 171.89 0.21 0.18 0.03 0 good 2.06 59.14 0 -0.04 0.38
951767006 3.95456 40 -0.34 0.24 3.95 6.59 0.94 0.52 98.2 156 3.84 152 850137840 0.43 0.99 6.95 85.17 0.32 0.19 0 0 good 2.75 83.91 0 -0.03 0.2
951767013 1.88857 50 -0.69 0.14 1.89 3.39 0.82 0.59 50.83 157 1.85 153 850137840 0.43 0.99 11.06 285.81 0.15 0.25 0.5 0 good 1.37 42.41 0.01 -0.02 1.11
951767020 1.77717 50 0 0.1 1.78 3.63 0.69 0.49 64.2 158 2.55 154 850137840 0.48 0.99 11.79 281.76 0.21 0.21 0.41 0.01 noise 0 51.89 0 -0.03 0.56
951767025 2.16158 80 0.07 0.03 2.16 2.65 0.25 0.62 62.81 159 2.45 155 850137840 0.53 0.99 31.06 288.69 0.18 0.25 0.5 0.01 noise 0.27 33.61 0.03 -0.03 0.36
951767033 0.14818 110 0.24 nan 0.15 3.6 0 0.45 63.73 160 2.27 156 850137840 0.59 0.95 24.07 121.07 0.22 0.19 0.39 0 noise 0.34 24.47 0.01 -0.04 1.76
951767038 1.78885 40 -0.69 0.14 1.79 6.23 0.97 0.55 120.54 161 3.95 157 850137844 0.42 0.99 6.68 93.56 0.36 0.18 0 0 good 0 65.92 0 -0.07 0.07
951767045 5.89758 30 nan 0.36 5.9 6.89 0.99 0.55 191.88 162 5.63 158 850137844 0.31 0.99 6.4 62.49 0.65 0.15 0 0 good 1.03 74.04 0 -0.08 0.61
951767050 11.6229 50 0 0.12 11.62 3.77 0.97 0.58 84.21 163 3.37 159 850137844 0.5 0.99 6.91 95.02 0.25 0.25 0.03 0 good 0.34 93.48 0 -0.05 0.3
951767056 5.01468 70 0.69 0.18 5.01 4.76 0.85 0.54 73.79 164 2.94 160 850137846 0.69 0.99 19.52 159.65 0.21 0.26 0.04 0 good 0.69 63.56 0.01 -0.04 0.19
951767061 4.74084 30 nan 0.06 4.74 3.88 0.85 0.62 70.38 165 2.79 161 850137846 0.61 0.99 9.93 256.56 0.18 0.23 0.06 0 good 0.69 59.92 0.01 -0.03 0.31
951767067 5.18054 50 -1.37 0.21 5.18 5.13 0.97 0.62 99.64 166 3.6 162 850137848 0.51 0.99 11.79 116.3 0.27 0.25 0 0 good 1.03 68.33 0 -0.04 0.03
951767074 8.54753 50 -0.34 0.14 8.55 2.95 0.94 0.45 71.01 167 2.91 163 850137848 0.71 0.99 8.23 179.9 0.23 0.22 0.37 0.01 good 0.69 88.01 0 -0.06 0.15
951767078 2.8839 40 -1.37 0.1 2.88 5.07 0.9 0.48 101.35 168 3.69 164 850137848 0.62 0.99 17.36 149.94 0.32 0.22 0 0 good 0 54.96 0 -0.06 0.08
951767086 17.4824 10 nan 0.14 17.48 nan nan 0.19 48.08 169 2.03 165 850137848 3.11 0.99 42.96 508.85 0.19 0.21 0.09 nan noise nan nan 0 -0.03 0.01
951767092 2.35626 60 -1.1 0.12 2.36 3.24 0.92 0.65 51.14 170 2.04 166 850137850 0.84 0.99 10.91 373.18 0.09 0.33 0.35 0 good 1.72 54.46 0 -0.03 0.17
951767098 6.15344 40 -0.69 0.29 6.15 nan nan 0.66 116.01 171 4.9 167 850137852 0.36 0.99 10.73 108.26 0.32 0.22 0 nan good 2.06 nan 0 -0.05 0
951767104 1.92845 50 -0.34 0.07 1.93 2.51 0.5 0.47 60.31 172 1.93 168 850137852 0.39 0.99 19.19 289.7 0.16 0.25 0.5 0 noise -0.34 34.89 0.03 -0.03 0.66
951767108 5.38793 70 0.55 0.09 5.39 nan nan 0.55 55.94 173 2.42 169 850137854 0.4 0.99 14.86 266.67 0.15 0.26 0.5 nan good 0.34 nan 0 -0.03 0.19
951767112 9.06679 50 -0.69 0.26 9.07 nan nan 0.54 113.64 174 4.8 170 850137854 0.53 0.99 7.74 88.74 0.31 0.27 0 nan good 0.34 nan 0 -0.07 0
951767120 4.13839 40 -1.03 0.08 4.14 nan nan 0.49 81.26 175 3.41 171 850137854 0.36 0.99 21.06 201.23 0.28 0.19 0.01 nan good 0.69 nan 0 -0.04 0.1
951767125 3.19928 10 nan 0.12 3.2 nan nan 0.23 69.9 176 2.83 172 850137854 0.26 0.99 33.83 588.51 0.31 0.1 0.09 nan noise nan nan 0 -0.06 0.04
951767133 3.54359 50 -0.69 0.11 3.54 nan nan 0.62 47.18 177 2.01 173 850137854 0.37 0.99 19.19 332.78 0.12 0.32 0.5 nan good -0.34 nan 0 -0.02 0.42
951767138 3.67855 50 -0.62 0.09 3.68 nan nan 0.52 40.44 178 2.04 174 850137856 0.8 0.99 21.55 420 0.11 0.32 0.5 nan good -0.69 nan 0 -0.03 0.55
951767144 4.2285 40 -0.34 0.18 4.23 nan nan 0.44 107.22 179 5.23 175 850137856 0.62 0.99 11.06 113.3 0.36 0.16 0 nan good -0.69 nan 0 -0.08 0.01
951767152 8.61593 50 -0.69 0.05 8.62 nan nan 0.55 54.33 180 2.7 176 850137856 0.7 0.99 14.44 200.78 0.14 0.34 0 nan good 0.69 nan 0 -0.04 0.04
951767157 1.58776 90 -1.59 -0 1.59 nan nan 0.51 42.15 181 2.11 177 850137856 0.8 0.99 27.35 413.73 0.11 0.32 0.5 nan noise 0 nan 0 -0.03 0.78
951767164 9.383 40 nan 0.09 9.38 2.65 0.89 1.55 76.05 182 0.29 178 850137974 3.65 0.99 62.36 919.61 0.01 1.51 0.21 0.03 noise -1.65 75.22 0.03 -0.06 0.1
951767169 3.17086 170 1.2 0.04 3.17 nan nan 2.01 18.45 183 0.59 179 850137992 0.25 0.99 38.78 1025.02 0.02 1.35 0.5 nan noise -0.57 nan 0 -0.16 0.27
951767177 2.97917 100 -1.37 0.01 2.98 nan nan 2.14 22.63 184 0.91 180 850137976 0.4 0.99 40.3 1062.45 0 1.36 0.5 nan noise 6.62 nan 0 -0.26 0.98
951767182 7.54455 110 4.46 0 7.54 2.03 0.79 0.85 31.88 185 0.47 181 850137982 0.65 0.96 51.06 582.43 0.02 0.98 0.5 0.04 noise -1.08 56.46 0.04 -0.01 0.17
951767190 0.09238 140 -0.2 nan 0.09 3.53 0.19 1.72 36.64 186 0.38 182 850137996 1.21 0.99 15.1 34.53 0.03 1 0.5 0 good 1.45 29.65 0.04 nan 49.92
951767195 2.75473 140 0.65 0.08 2.75 4.76 0.96 0.21 36.98 187 1.07 183 850137992 0.44 0.99 28.89 528.07 0.17 0.12 0.46 0 good 2.39 50.44 0.03 -0.04 5.18
951767202 3.80731 60 -0.41 0.05 3.81 2.8 0.87 0.21 436.46 188 5.78 184 850138002 0.39 0.84 46.71 737.76 1.89 0.11 0.04 0 noise -0.34 44.53 0.06 -0.32 0.84
951767209 5.08578 50 -0.34 0.24 5.09 6.11 0.98 0.21 390.08 189 5.6 185 850138002 0.36 0.93 20.96 148.6 1.61 0.12 0 0 good 0 62.96 0.01 -0.26 0.04
951767217 0.1054 50 -1.44 nan 0.11 3.95 0.94 0.32 143.94 190 2.77 186 850138002 0.44 0.33 39.12 15.37 0.47 0.27 0 0 good 1.37 42.53 0 -0.13 0
951767223 6.24179 100 -0.14 0.38 6.24 8.86 1 0.54 117.74 191 3.26 187 850138006 0.42 0.99 17.72 59.5 0.35 0.29 0 0 good -0.24 147.5 0 -0.05 0
951767230 0.08897 50 -1.03 nan 0.09 6 0.94 0.29 193.24 192 3.85 188 850138002 0.4 0.19 4.3 9.64 0.86 0.25 0.06 0 good 0.69 73.11 0 -0.11 0
951767242 10.0404 80 0.41 0.2 10.04 5.89 1 0.66 56.36 193 1.82 189 850138010 0.21 0.99 13.67 149.29 0.18 0.19 0 0 good 0.34 110.43 0 -0.02 0.02
951767247 1.57566 80 -0.21 0.2 1.58 6.62 0.99 0.51 78.09 194 2.33 190 850138014 0.34 0.99 19.06 154.9 0.26 0.16 0 0 good 0.34 82.46 0 -0.03 0
951767253 8.11517 130 -0.56 0.14 8.12 4.34 0.99 0.56 48.05 195 1.03 191 850138022 0.29 0.99 13.1 135.97 0.15 0.25 0.24 0 good 0.14 111.97 0 -0.03 0.07
951767258 4.49191 150 -0.1 0.11 4.49 2.98 0.92 0.33 50.82 196 1.08 192 850138018 0.64 0.99 16.5 242.6 0.19 0.18 0.5 0 noise 0.16 52.03 0.02 -0.04 1.25
951767263 3.47787 170 -0.03 0.04 3.48 2.86 0.87 2.02 34.98 197 0.73 193 850138016 1.59 0.99 34.44 1122.43 0.01 1.39 0.35 0.01 noise -3.77 52.62 0.02 -0.56 0.39
951767269 1.71785 170 -0.21 -0 1.72 1.36 0.09 1.84 33.63 198 0.49 194 850138016 0.09 0.99 40.22 1356.01 0.01 1.63 0.3 0.02 noise 3.19 22.2 0.23 -0.33 1.56
951767274 0.48785 170 0 -0.01 0.49 2.92 0.14 2.09 96.72 199 1.06 195 850138024 1.52 0.99 90.69 2143.35 0.04 1.3 0.01 0 noise -9 19.54 0.12 -1.92 0.81
951767280 13.4059 100 -1 0.15 13.41 6.45 1 0.27 61.11 200 1.97 196 850138016 0.4 0.99 13.59 151.5 0.28 0.16 0.02 0 good 0.21 129.05 0 -0.04 0.04
951767285 1.1801 90 0.82 0.26 1.18 8.61 1 0.26 90.48 201 2.54 197 850138018 2.26 0.99 48.34 330.9 0.4 0.18 0 0 good 2.54 102.1 0 -0.08 0.03
951767291 7.60314 70 -0.69 0.03 7.6 4.05 0.99 0.18 162.33 202 1.66 198 850138024 0.53 0.99 65.96 477.36 0.68 0.11 0.5 0.01 noise 0 67.14 0.01 -0.16 0.14
951767297 5.39754 70 -0.62 0.02 5.4 3.78 1 0.23 108.69 203 1.62 199 850138024 0.51 0.99 51.07 366.36 0.51 0.14 0.4 0 noise -0.48 72.05 0 -0.08 0.1
951767304 1.49341 70 -11.87 0.07 1.49 4.68 0.93 0.45 76.5 204 0.91 200 850138030 0.5 0.99 40.7 426.76 0.27 0.14 0.34 0 good -0.41 43.65 0.02 -0.03 1.29
951767310 20.5422 40 -0.34 0.3 20.54 12.65 1 0.22 659.41 205 8.25 201 850138032 0.55 0.9 25.3 79.93 2.83 0.14 0 0 good 0 577.83 0 -0.6 0
951767318 0.76107 70 0.96 0.03 0.76 3.1 0.56 0.69 73.53 206 0.82 202 850138036 0.2 0.99 37.58 272.55 0.25 0.16 0.05 0 good 1.17 24.89 0.18 -0.02 9.3
951767322 0.1455 160 -6.38 nan 0.15 5.14 0.55 0.7 29.87 207 0.17 203 850138032 0.89 0.88 30.73 206.97 0.07 0.12 0.03 0 good 1.93 34.69 0.01 -0.03 1.83
951767329 3.09563 150 -0.25 0.04 3.1 1.85 0.2 0.29 38.19 208 0.45 204 850138036 0.09 0.99 25.88 471.2 0.14 0.22 0.21 0.03 noise -0.17 26.25 0.25 -0.01 2.15
951767334 5.63676 160 -0.18 0.03 5.64 2.73 0.7 0.22 40.94 209 0.36 205 850138026 0.69 0.99 71.93 429.93 0.17 0.11 0.4 0.05 noise 0.08 40.07 0.12 -0.03 0.5
951767340 4.63348 160 -3.46 0.03 4.63 1.49 0.38 2.01 23.35 210 0.79 206 850138052 0.43 0.99 21.55 580.42 0.01 1.33 0.5 0.12 noise 6.55 37.61 0.22 -0.29 0.09
951767346 6.02128 150 3.38 0.02 6.02 2.02 0.55 2.02 23.96 211 0.62 207 850138056 1.43 0.99 24.24 643.52 0 1.4 0.42 0.07 noise -7.71 40.01 0.11 -0.41 0.14
951767351 1.51118 130 1.21 0.01 1.51 1 0.11 1.88 35.9 212 0.92 208 850138056 0.7 0.99 31.02 1081.97 0.01 1.57 0.03 0.06 noise 5.92 27.96 0.45 -0.69 0.05
951767358 0.50418 170 3.02 0.16 0.5 2.02 0.06 1.95 52.82 213 0.78 209 850138056 1.13 0.99 66.13 1632.46 0 1.52 0.01 0.01 noise -6.43 17.31 0.26 -0.84 0.61
951767364 0.4586 100 -4.34 0.12 0.46 1.82 0.17 2.16 80.47 214 1.43 210 850138056 0.57 0.99 50.3 909.04 0.01 1.39 0.03 0.01 noise 2.75 17.94 0.73 -1.71 2.58
951767370 5.1362 100 -5.71 0.04 5.14 1.26 0.49 2.03 26.44 215 0.81 211 850138058 0.63 0.99 14.56 400.85 0.01 1.18 0.39 0.3 noise 0.69 44.85 0.35 -0.38 0.25
951767376 3.00521 170 -0.03 0.06 3.01 2.44 0.64 1.21 17.89 216 0.64 212 850138090 0.46 0.99 20.48 660.27 0.01 0.95 0.5 0.05 noise 1.72 40.16 0.18 -0.02 4.8
951767383 2.80598 10 nan 0.19 2.81 3.9 0.89 2.62 52.06 217 2.03 213 850138088 0.05 0.99 3.46 136.69 -0 0.78 0 0.02 noise nan 87.73 0.02 -1.12 4.43
951767389 0.93684 10 nan 0.07 0.94 3.95 0.81 2.09 52.69 218 1.62 214 850138088 0.03 0.99 9.74 311.76 0.21 0.21 0.06 0.01 noise nan 58.42 0.01 nan 0.26
951767395 1.53702 10 nan 0.08 1.54 3.86 0.8 0.69 52.31 219 1.85 215 850138088 0.02 0.99 10.74 243.44 0.06 0.51 0 0.02 noise nan 47.77 0.04 -0 0.1
951767402 1.03677 10 nan 0.15 1.04 5.7 1 1.88 52.01 220 1.49 216 850138088 0.01 0.99 33.78 1195.2 0 1.55 0 0 noise nan 104.96 0 nan 0
951767408 0.03968 10 nan nan 0.04 4.71 0.4 0.91 51.34 221 1.65 217 850138088 0.01 0.82 15.49 0 0 1.59 0.02 0 noise nan 38.43 0 nan 0
951767415 0.16286 170 -6.36 nan 0.16 7.67 0.97 1.07 4.64 222 0.07 218 850138036 0.68 0.96 62.46 376.91 0 nan 0.01 0 noise 2.58 63.32 0 -0 1.46
951767422 3.12963 170 -2.67 0.03 3.13 2.15 0.57 2.06 22.74 223 0.87 219 850138092 0.26 0.99 80.54 556.11 0.05 0.36 0.5 0.08 noise -0.35 40.61 0.17 -0.16 4.15
951767428 0.00806 170 -3.82 nan 0.01 4.22 0.11 0.6 38.58 224 1.14 220 850138096 0.39 0.39 nan 0 0.09 0.36 0.5 0 noise -1.81 47.67 0 -0.01 0
951767433 0.48826 170 -7.03 -0.02 0.49 2.17 0.2 1.68 16.61 225 0.47 221 850138098 1.47 0.93 50.55 164.35 0.01 0.49 0.5 0.01 noise -0.38 23.76 0.24 -0.14 49.06
951767438 4.72493 100 0.22 0.1 4.72 4.33 0.99 0.41 38.76 226 1.64 222 850138110 0.21 0.99 43.22 184.28 0.14 0.19 0.11 0.01 good 0.41 67.55 0.01 -0.01 0.11
951767443 0.44 30 -3.43 -0.03 0.44 5.76 0.95 0.52 46.88 227 1.84 223 850138104 3.2 0.99 75.5 645.03 0.1 0.21 0.29 0 noise 2.75 61.74 0 -0.02 0.8
951767450 0.01478 60 -2.06 nan 0.01 nan nan 0.62 59.2 228 2.05 224 850138104 3.71 0.37 58.25 29.42 0.12 0.25 0.42 0 noise 1.03 nan nan -0.01 0
951767455 2.51437 140 -1.53 0.07 2.51 2.84 0.81 0.73 28.62 229 1.21 225 850138106 0.01 0.99 47.73 316.06 0.06 0.41 0.5 0.02 good -1.57 47.65 0.05 -0 0.9
951767461 1.6666 120 -1.44 0.07 1.67 3.46 0.8 0.69 35.3 230 1.55 226 850138108 0.32 0.96 28.63 349.68 0.08 0.32 0.08 0.01 good -1.64 47.41 0.03 -0.01 0.68
951767468 6.65524 110 -2.06 0.14 6.66 3.24 0.95 0.71 36.6 231 1.52 227 850138110 0.69 0.99 33.65 279.16 0.05 0.36 0.1 0.01 noise -0.77 64.28 0.01 -0 0.27
951767474 4.99029 170 -1.57 0.02 4.99 2.08 0.59 0.77 24.16 232 0.96 228 850138116 0.2 0.99 39.19 341.26 0.04 0.48 0.5 0.03 noise -1.8 44.47 0.05 -0 0.57
951767481 2.13409 140 -1.81 0.09 2.13 2.67 0.66 0.66 28.92 233 1.24 229 850138114 0.23 0.99 53.12 261.51 0.07 0.38 0.14 0.01 good -1.59 36.38 0.07 -0.01 0.8
951767487 15.1874 50 -0.34 0.08 15.19 4.62 0.98 0.25 48.87 234 2.01 230 850138114 0.37 0.99 30.84 355.49 0.21 0.12 0 0 good 0.34 86.39 0.01 -0.05 0.03
951767493 0.00765 160 -3.03 nan 0.01 5.54 nan 0.26 60.36 235 1.65 231 850138114 2 0.28 nan 0 0.25 0.15 0.5 0 noise -2.93 70.92 0 -0.04 0
951767500 2.84287 140 -2.26 0.04 2.84 2.96 0.78 0.56 44.4 236 1.8 232 850138116 0.24 0.99 39.63 217.49 0.12 0.3 0.05 0.01 good -1.72 40.6 0.04 -0 0.41
951767507 1.90045 170 -0.02 0.03 1.9 2.26 0.5 1.39 23.73 237 0.72 233 850138116 0.41 0.99 34.95 656.73 0 0.99 0.5 0.02 noise 1.56 35.08 0.09 -0.01 16.39
951767514 1.88309 110 -0.89 0.12 1.88 2.98 0.89 0.92 43.35 238 1.77 234 850138114 0.53 0.99 36.34 326.71 0.08 0.26 0.03 0 good 0.48 46.58 0.02 -0.01 0.54
951767520 2.06217 80 -1.85 0.28 2.06 8.81 0.99 0.81 85.24 239 3.58 235 850138120 0.31 0.88 30.33 59.79 0.2 0.29 0 0 good 0.76 126.45 0 -0.03 0.02
951767526 2.5247 170 -0.85 0.04 2.52 1.86 0.41 1.41 29.91 240 0.68 236 850138136 0.16 0.99 33.28 622.19 0.02 0.91 0.5 0.02 noise -0.7 35.88 0.07 -0.02 6.13
951767532 6.72251 130 -1.1 0.04 6.72 2.35 0.79 0.66 36.8 241 1.5 237 850138122 0.6 0.99 59.98 303.32 0.06 0.33 0.16 0.02 good -1.51 46.67 0.05 -0 0.47
951767538 0.62498 120 -1.24 -0.03 0.62 3.18 0.93 0.69 48.42 242 2.07 238 850138130 0.12 0.99 38.89 163.27 0.12 0.36 0.01 0 good -1.24 51.37 0 -0.01 0
951767544 0.76841 140 -0.77 0.19 0.77 5.43 0.94 0.77 118.16 243 3.19 239 850138142 0.29 0.98 24.97 364.01 0.35 0.21 0 0 good 4.83 60.01 0 -0.04 0.46
951767547 0.21701 110 -1.44 nan 0.22 3.24 0.59 0.6 71.96 244 2.48 240 850138126 0.24 0.97 34.37 443.25 0.24 0.21 0.26 0 noise -0.93 33.53 0.02 -0.02 4.93
951767552 0.27684 90 -0.69 -0.03 0.28 nan nan 0.66 64.15 245 0.56 241 850138126 0.03 0.51 37.91 201.76 0.04 0.38 0.08 0 noise -1.74 nan nan -0 3.03
951767556 2.96853 170 -2.07 0.04 2.97 2.6 0.87 0.69 40.27 246 1.31 242 850138122 0.64 0.99 44.91 295.89 0.07 0.3 0.02 0 noise -1.48 44 0.02 -0.01 0.56
951767562 0.29637 120 -1.55 nan 0.3 3.71 0.89 0.71 100.94 247 2.09 243 850138136 0.33 0.98 43.71 393.97 0.19 0.26 0.06 0 noise 0.21 46.09 0 -0.02 2.65
951767566 0.71446 130 -1.62 0.01 0.71 3.72 0.7 0.67 75.4 248 2.31 244 850138132 0.23 0.99 43.63 389.66 0.24 0.21 0.01 0 good -0.61 47.39 0 -0.01 0.91
951767573 7.00834 90 -1.82 -0.03 7.01 3.71 1 0.95 86.65 249 2.81 245 850138138 0.19 0.99 44.53 222.47 0.24 0.22 0 0 good -0.27 92.27 0 -0.01 0.01
951767580 0.01715 80 -0.96 nan 0.02 4.95 0 0.71 163.18 250 3.3 246 850138132 0.33 0.53 nan 0 0.48 0.19 0 0 good -0.62 30.62 0 -0.05 0
951767586 5.66043 70 -0.69 -0.03 5.66 2.6 0.85 0.49 58.32 251 0.65 247 850138134 0.35 0.71 34.43 174.22 0.07 0.4 0.08 0.01 good -0.21 52.28 0.02 -0.01 0.15
951767594 3.2216 130 -1.33 -0.05 3.22 2.34 0.84 0.7 50.84 252 1.36 248 850138150 0.25 0.99 62.13 469.7 0.17 0.18 0.04 0.01 good -0.14 46.92 0.02 -0.02 0.49
951767599 1.25687 130 -2.95 0.13 1.26 4.89 0.99 0.65 80.99 253 2.24 249 850138136 0.3 0.99 18.14 377.29 0.18 0.32 0.06 0 noise -1.04 55.17 0 -0.02 0.44
951767606 1.26183 110 0.2 0.08 1.26 3.96 0.9 0.45 55.87 254 1.43 250 850138136 0.27 0.99 40.41 499.22 0.22 0.18 0.34 0 good 0.34 54.59 0 -0.02 2.65
951767612 6.88134 130 -1.63 0.21 6.88 4.09 0.95 0.73 82.98 255 2.59 251 850138140 0.39 0.99 58.4 273.99 0.21 0.22 0 0 good -0.34 75.51 0 -0.03 0.03
951767618 4.13209 140 -1.24 0.03 4.13 2.73 0.85 0.73 49.69 256 1.5 252 850138138 0.45 0.99 55.11 237.06 0.09 0.33 0.05 0 good -0.85 50.38 0.01 -0 0.22
951767624 3.92211 90 -1.37 0.08 3.92 3.35 0.96 0.7 86.56 257 2.65 253 850138138 0.4 0.99 78.24 272.2 0.22 0.25 0 0 good -0.64 62.47 0 -0.02 0.04
951767631 0.00496 170 -3.07 nan 0 2.91 nan 0.19 68.73 258 0.89 254 850138142 0.7 0.23 nan 0 0.28 0.59 0.5 0 good -1.49 33.74 0 -0.04 0
951767636 0.19076 60 0.82 0.1 0.19 4.41 0.17 0.18 84.53 259 2.16 255 850138142 0.9 0.68 38.77 170.34 0.31 0.51 0.02 0 noise 1.37 30.85 0.01 -0.13 1.06
951767643 4.95309 120 -3.02 0.19 4.95 4.04 0.95 0.74 66.89 260 1.99 256 850138140 0.36 0.99 50.07 248.01 0.15 0.3 0 0 good -0.79 53.86 0.01 -0.02 0.03
951767649 6.09692 110 -2.39 0.12 6.1 2.43 0.89 0.77 64.09 261 2.01 257 850138140 0.28 0.99 64.71 232.59 0.18 0.23 0.01 0.01 good 0.16 54.34 0.01 -0.02 0.38
951767655 1.171 70 -0.86 0.22 1.17 7.93 0.98 0.88 179.72 262 4.51 258 850138142 0.21 0.99 42 228.68 0.61 0.15 0 0 good 0 109.71 0 -0.04 0.03
951767661 7.66545 80 -1.2 -0.01 7.67 3 0.87 0.45 49.75 263 0.79 259 850138142 0.34 0.67 49.61 187.45 0.1 0.44 0.25 0.01 good nan 59.53 0.02 -0.01 0.25
951767667 1.09298 50 -1.24 0.05 1.09 6.01 0.97 0.78 148.78 264 3.4 260 850138142 0.2 0.99 33.85 96.98 0.51 0.15 0 0 good 1.37 102.26 0 -0.03 0.03
951767674 0.24584 60 -1.3 -0.09 0.25 3.4 0.06 0.59 75.83 265 2.04 261 850138142 0.74 0.29 16.37 62.29 0.18 0.25 0.06 0 good 3.43 26.32 0.02 -0.1 1.28
951767681 0.22228 60 -1.3 -0.05 0.22 3.36 0.05 0.62 70.75 266 1.84 262 850138142 0.81 0.25 15.51 56.29 0.16 0.26 0.02 0 good 3.43 25.65 0.01 -0.11 0
951767688 1.44722 60 1.44 0.06 1.45 5.93 0.93 0.19 76.39 267 1.81 263 850138142 0.87 0.58 15.99 80.17 0.28 0.59 0 0 noise 1.37 72.62 0 -0.11 0.09
951767694 0.24387 60 1.03 nan 0.24 3.64 0.12 0.18 83.3 268 2.37 264 850138142 0.97 0.37 12.17 38.67 0.31 0.49 0.01 0 noise 1.37 27.46 0.01 -0.13 0.65
951767700 0.04929 60 0.89 nan 0.05 4.68 0 0.19 86.6 269 2.23 265 850138142 0.8 0.35 7.03 13.28 0.35 0.48 0.05 0 good 1.37 24.81 0 -0.12 0
951767707 0.01829 140 -3.13 nan 0.02 2.23 0 0.81 40.32 270 0.7 266 850138142 1.13 0.55 9.09 0 0.07 1.24 0.5 0 noise -0.69 16.23 0.04 -0.01 0
951767713 17.364 120 -0.71 0.12 17.36 4.23 0.99 0.25 69.82 271 2.06 267 850138144 0.66 0.99 41.5 168 0.33 0.18 0.15 0 good -0.1 89.95 0 -0.07 0.08
951767719 1.35949 50 -0.69 0.12 1.36 7.02 0.99 0.98 201.53 272 3.42 268 850138148 0.28 0.91 57.38 171.84 0.76 0.18 0 0 good -0.34 147.57 0 -0.05 0
951767725 14.6946 70 -2.4 0.09 14.69 2.9 0.81 0.7 49.89 273 1.45 269 850138148 0.37 0.99 40.52 230.93 0.12 0.25 0.02 0.02 good -0.96 59.67 0.04 -0.01 0.14
951767730 13.7188 90 -3.09 0.01 13.72 2.63 0.8 0.8 28.5 274 0.86 270 850138148 0.35 0.99 62.19 287.69 0.07 0.37 0.09 0.02 good -1.89 60.97 0.02 -0.01 0.07
951767738 2.12593 90 -1.03 0.03 2.13 2.25 0.71 0.65 67.12 275 1.91 271 850138148 0.24 0.99 60.51 281.6 0.23 0.19 0.01 0.01 good -0.48 42.38 0.02 -0.01 0.38
951767743 1.28085 110 -1.37 0.23 1.28 3.72 0.92 0.59 115.49 276 2.22 272 850138128 0.31 0.99 58.89 443.26 0.17 0.27 0 0 noise -0.8 46.64 0.01 -0.01 1.53
951767750 1.1275 150 -2.07 -0.06 1.13 2.08 0.33 0.67 31.57 277 0.8 273 850138150 0.34 0.7 72.78 348.57 0.05 0.34 0.09 0 good -0.34 26.86 0.05 -0.01 1.34
951767757 0.86709 120 -1.19 -0.08 0.87 3.75 0.91 0.8 66.06 278 1.72 274 850138150 0.29 0.99 10.93 215.21 0.17 0.27 0.16 0 good 0.14 44.67 0.01 -0.01 0.98
951767763 0.25875 100 -0.98 -0.06 0.26 2.19 0.2 0.58 67.45 279 1.68 275 850138142 0.76 0.32 15.82 96.02 0.15 0.29 0.5 0 good -0.89 23.57 0.03 -0.08 8.1
951767770 2.86085 80 -0.89 0.05 2.86 4.07 0.98 0.77 117.16 280 3.34 276 850138150 0.17 0.99 62.68 229.39 0.4 0.16 0 0 good -0.27 87.99 0 -0.02 0.02
951767776 2.16685 170 -1.08 -0.01 2.17 2.14 0.4 1 49.39 281 0.8 277 850138160 1.02 0.99 41.2 767.92 0.03 1.07 0.48 0 noise -0.19 32.87 0.06 nan 6.08
951767782 1.31753 80 -0.48 0.19 1.32 4.19 0.79 0.63 158.8 282 4.03 278 850138152 0.35 0.99 41.6 173.48 0.51 0.19 0 0 good -0.55 45.94 0.01 -0.07 0.65
951767789 4.99897 90 -0.69 0.13 5 3.32 0.82 0.62 67.44 283 1.77 279 850138152 0.3 0.99 36.34 164.54 0.2 0.25 0.39 0.01 good -0.83 50.62 0.01 -0.03 0.52
951767795 2.74997 50 0 0.11 2.75 3.2 0.85 0.52 75.32 284 1.75 280 850138152 0.33 0.99 38.38 196.36 0.27 0.16 0.02 0 good -0.21 46.16 0.01 -0.05 0.11
951767803 4.23677 170 -1.43 0.03 4.24 1.56 0.68 0.67 41.14 285 1.06 281 850138154 0.37 0.99 48.83 390.72 0.1 0.3 0.42 0.01 good -0.55 44.1 0.03 -0.01 0.44
951767810 2.37765 160 -1.58 0.05 2.38 1.47 0.44 0.66 51.96 286 1.32 282 850138154 0.44 0.99 53.98 467.51 0.15 0.26 0.5 0.01 good -0.3 31.49 0.09 -0.02 1.11
951767821 4.38216 80 -2.75 0.09 4.38 5.07 1 0.78 50.64 287 1.39 283 850138148 0.37 0.93 19.68 129.48 0.13 0.21 0.01 0 good -0.77 79.55 0 -0.01 0.01
951767827 4.35674 90 -0.82 0.16 4.36 5.36 1 0.74 131.51 288 3.09 284 850138162 0.36 0.99 48.51 398 0.46 0.14 0 0 good -0.07 89.74 0 -0.02 0.01
951767832 3.53626 70 -0.48 0.09 3.54 3.88 0.98 0.71 93.11 289 2.38 285 850138156 0.19 0.99 46.45 194.3 0.31 0.19 0 0 good -0.69 66.16 0 -0.01 0.2
951767838 2.72631 70 -0.48 0.1 2.73 1.79 0.76 0.69 105.12 290 2.28 286 850138160 0.3 0.99 30.53 219.61 0.34 0.21 0.26 0 good -0.41 42.45 0.02 -0.02 0.67
951767845 0.74929 160 -4.69 nan 0.75 2.4 0.08 1.33 61.25 291 0.9 287 850138150 0.91 0.99 51.23 1024.32 0.02 0.92 0.46 0 noise 0.58 19.76 0.2 -0.05 57.97
951767852 0.26867 110 -1.08 nan 0.27 3.85 0.69 0.84 146.74 292 3.44 288 850138158 0.19 0.95 68.8 281.19 0.53 0.14 0.02 0 noise -0.34 35.99 0.01 -0.03 1.07
951767857 1.92391 120 -1.37 0.04 1.92 2.36 0.7 0.67 55.17 293 1.53 289 850138158 0.36 0.99 33.02 335.35 0.16 0.23 0.5 0 good -0.48 40.83 0.01 -0.02 1.09
951767862 0.6289 170 -1.67 -0.09 0.63 2.45 0.36 0.65 29.13 294 0.75 290 850138150 0.3 0.82 92.36 352.76 0.06 0.34 0.35 0 noise -0.6 29.54 0.03 -0.01 3.13
951767868 2.15331 170 -7.44 0.03 2.15 nan nan 2.02 48.77 295 0.99 291 850138166 1.4 0.99 43.66 1530.26 0.06 0.47 0.5 0 noise 0.19 nan nan -0 9.72
951767873 2.78717 70 -0.48 0.05 2.79 2.93 0.52 0.45 119.77 296 2.45 292 850138160 0.4 0.99 44.17 256.24 0.43 0.21 0.02 0 good 1.17 32.39 0.06 -0.04 0.55
951767879 1.65482 40 0.34 0.02 1.65 3.31 0.93 0.36 78.77 297 1.82 293 850138160 0.32 0.98 48.91 273.2 0.31 0.14 0.17 0 good 0.69 48.08 0.01 -0.05 0.04
951767884 0.02883 90 -0.76 nan 0.03 3.57 0 0.91 71.58 298 1.77 294 850138162 0.44 0.69 6.61 6.74 0.17 0.25 0.03 0 good -0.62 36.78 0 -0.01 0
951767892 0.20926 70 -0.62 nan 0.21 4.24 0.36 0.87 143.74 299 3.34 295 850138164 0.22 0.72 15.64 44.12 0.51 0.18 0 0 good 0 37.14 0 -0.04 1.77
951767897 26.7566 70 -0.69 0.07 26.76 3.94 0.98 0.33 122.16 300 3.2 296 850138164 0.53 0.99 50.67 64.23 0.5 0.18 0 0.01 good 1.1 85.82 0.01 -0.09 0
951767903 4.96601 100 -0.55 0.06 4.97 2.11 0.79 0.59 73.02 301 1.69 297 850138160 0.43 0.99 70.68 210.46 0.22 0.23 0.33 0.01 good -0.69 49.02 0.02 -0.04 0.53
951767907 1.15405 100 -0.07 0.22 1.15 4.49 0.9 0.54 92.98 302 2.72 298 850138166 0.4 0.99 47.13 214.61 0.33 0.23 0 0 good 0.96 54.06 0 -0.04 0
951767915 2.33498 130 -1.25 0.04 2.33 2.28 0.72 0.67 47.36 303 1.35 299 850138166 0.33 0.99 37.93 401.81 0.12 0.29 0.5 0 good 0.48 40.92 0.02 -0 0.4
951767920 11.689 80 -0.69 0.14 11.69 5.75 1 0.7 105.86 304 2.96 300 850138166 0.36 0.99 51.4 136.44 0.31 0.21 0 0 good -0.48 107.17 0 -0.03 0
951767927 4.05283 110 -0.69 0.04 4.05 2.11 0.61 0.58 68.12 305 1.44 301 850138160 0.57 0.99 54.26 267.27 0.19 0.27 0.5 0.01 good -0.86 36.17 0.05 -0.04 0.84
951767933 1.48814 70 -1.82 0.16 1.49 7.19 0.99 0.78 193.04 306 3.58 302 850138168 0.21 0.94 34.74 83.77 0.74 0.12 0 0 good -0.41 93.64 0 -0.04 0
951767939 3.34074 80 -0.69 0.24 3.34 4.51 0.97 0.59 229.84 308 4.67 303 850138168 0.43 0.99 49.36 76.45 0.78 0.21 0 0 good -0.07 73.87 0 -0.13 0.1
951767945 4.65301 110 -0.62 0.1 4.65 2.82 0.76 0.51 63.57 309 1.42 304 850138168 0.52 0.99 38.17 176.12 0.19 0.27 0.06 0.01 good -0.83 41.23 0.03 -0.04 0.14
951767950 11.2101 80 -0.41 0.05 11.21 2.69 0.86 0.38 95.96 310 2.31 305 850138168 0.49 0.99 44.41 85.6 0.39 0.16 0.08 0.02 good 0.34 53.81 0.02 -0.07 0.15
951767956 3.27482 90 -0.48 0.11 3.27 4.1 0.93 0.58 118.11 311 2.3 306 850138168 0.37 0.99 42.3 117.88 0.39 0.22 0 0 good -0.76 45.81 0.01 -0.05 0.12
951767960 7.71826 110 -0.86 0.01 7.72 1.95 0.7 0.49 70.92 312 1.75 307 850138168 0.37 0.99 44.55 124.64 0.25 0.23 0.36 0.02 good -0.06 43.14 0.04 -0.03 0.3
951767966 7.05711 60 0.21 0.07 7.06 3.83 0.92 0.62 104.41 313 2.2 308 850138170 0.39 0.99 39.88 514.91 0.23 0.22 0.02 0 good 0.69 55.25 0.02 -0.02 0.1
951767973 1.25284 120 -1.04 0.2 1.25 4.39 0.94 0.78 103.97 314 3.15 309 850138170 0.37 0.99 42.79 315.6 0.33 0.22 0 0 good -0.55 76 0 -0.03 0.02
951767979 2.99633 130 -1.03 0.1 3 2.82 0.81 0.69 60.46 315 1.64 310 850138172 0.35 0.99 67.34 319.82 0.18 0.25 0.43 0 good 0 59.95 0 -0.03 0.41
951767984 0.48289 110 -1.05 nan 0.48 4.03 0.86 0.56 127.28 316 3.34 311 850138172 0.38 0.99 41.63 135.46 0.41 0.19 0 0 good 0 55.48 0 -0.05 0
951767991 5.21691 60 0 0.07 5.22 3.12 0.93 0.54 136.74 317 3.92 312 850138174 0.29 0.99 50.67 74.44 0.48 0.18 0 0 good 0 68.04 0 -0.05 0.01
951767997 2.56841 110 -0.76 0.04 2.57 2.76 0.9 0.62 60.57 318 1.75 313 850138174 0.39 0.99 50.55 244.8 0.16 0.27 0.5 0 good -0.76 55.49 0 -0.03 0.28
951768004 4.48581 90 -0.33 0.21 4.49 5.44 0.98 0.59 130.54 320 3.7 314 850138174 0.35 0.99 46.69 103.15 0.42 0.15 0 0 good 0.21 95.05 0 -0.07 0
951768010 4.42339 90 -0.14 0.03 4.42 2.96 0.67 0.4 69.26 321 1.91 315 850138176 0.48 0.99 36.56 232.21 0.26 0.19 0.5 0.01 good -0.21 42.65 0.03 -0.04 0.37
951768018 8.212 120 -0.03 0.06 8.21 2.96 0.86 0.52 48.79 322 1.39 316 850138176 0.68 0.99 45.49 223.92 0.13 0.4 0.44 0.01 good -0.89 54.15 0.02 -0.04 0.45
951768023 4.26932 110 -0.78 0.07 4.27 3.4 0.79 0.62 56.06 323 1.46 317 850138176 0.74 0.99 42.71 218.54 0.09 0.4 0.36 0 good -0.31 45.47 0.02 -0.03 0.22
951768030 2.22027 70 -0.48 0.1 2.22 3.18 0.87 0.66 82.89 324 2.5 318 850138176 0.33 0.99 50 131.39 0.27 0.18 0.01 0 good 0.07 51.59 0 -0.03 0.05
951768035 3.24588 170 0.68 0.07 3.25 2.11 0.42 1.1 48.28 325 1.09 319 850138176 0.98 0.99 40.58 585.63 0.09 0.77 0.5 0.02 noise -0.58 37.57 0.06 -0.04 2.73
951768042 3.34725 160 0.07 0.05 3.35 2.74 0.5 0.41 53.97 326 1.24 320 850138176 0.24 0.99 53.73 404.1 0.2 0.25 0.5 0.01 noise 0.07 37.09 0.05 -0 2.18
951768047 2.89165 130 -1.02 0.09 2.89 3.1 0.85 0.51 82.2 327 2.27 321 850138172 0.44 0.99 50.67 223.88 0.3 0.19 0.01 0 good -0.48 60.03 0 -0.05 0.11
951768054 18.1724 70 -0.07 0.07 18.17 3.87 0.97 0.25 55.66 328 2 322 850138182 0.68 0.99 39.8 143.33 0.25 0.14 0.06 0.02 good -0.27 87.99 0.01 -0.06 0.03
951768060 0.46429 170 -3.18 0.01 0.46 3.45 0.27 1.03 76.32 329 1.21 323 850138176 1.49 0.99 30.41 807.27 0.04 1.04 0.05 0 noise -0.05 23.36 0.14 nan 30.37
951768067 3.65075 130 -0.05 0.08 3.65 3.19 0.74 0.34 63.57 330 1.83 324 850138184 0.65 0.99 41.82 267.21 0.26 0.23 0.5 0.01 good -0.14 44.8 0.03 -0.05 1.17
951768073 2.28259 170 -6.94 0.03 2.28 2.42 0.32 1.63 41.85 331 0.85 325 850138176 1.62 0.99 31.36 492.57 0.03 1.07 0.46 0.02 noise -1.01 32.86 0.08 nan 4.99
951768080 1.55624 90 0.14 0.06 1.56 2.75 0.63 0.47 46.33 332 1.46 326 850138184 0.41 0.99 38.55 315.07 0.17 0.18 0.28 0 good -0.27 37.52 0.04 -0.01 1.04
951768086 0.1579 30 0 0.04 0.16 6.2 0.92 0.33 63.83 333 2.54 327 850138188 0.2 0.61 11.12 61.95 0.26 0.12 0.34 0 good 0 68.38 0 -0.02 0
951768093 3.65344 170 -0.17 0.02 3.65 2.09 0.37 0.33 44.61 334 1.53 328 850138190 0.32 0.99 35.59 336.56 0.19 0.25 0.45 0.03 good 0.01 35.11 0.13 -0.02 1.35
951768098 4.65538 130 -0.09 0.01 4.66 2.54 0.48 0.29 49.66 335 1.82 329 850138190 0.68 0.99 45.17 262.18 0.22 0.22 0.5 0.04 noise -0.07 42.51 0.07 -0.04 0.26
951768105 13.1174 40 0 0.06 13.12 3.11 0.9 0.29 57.81 336 2.11 330 850138190 0.28 0.99 37.22 247.99 0.23 0.11 0.04 0.04 good 0 63.36 0.04 -0.03 0.03
951768109 2.4225 10 nan 0.08 2.42 5.23 1 0.25 66.16 337 2.56 331 850138192 0.34 0.99 17.04 232.86 0.26 0.1 0.38 0 noise nan 61.8 0 -0.05 0.19
951768115 0.42089 30 -3.43 -0.04 0.42 6.97 0.8 0.32 60.11 338 2.66 332 850138192 3.67 0.84 33.88 425.4 0.19 0.14 0.03 0 noise 2.06 125.6 0 -0.03 2.19
951768121 0.28893 20 0 0.09 0.29 6.69 0.94 0.25 67.22 339 2.99 333 850138200 0.55 0.96 10.25 103.64 0.28 0.11 0.34 0 noise nan 54.66 0 -0.06 0.46
951768127 3.07114 20 nan 0.1 3.07 7.08 1 0.16 82.18 340 3.46 334 850138208 2.42 0.76 37.41 412.04 0.31 0.11 0.27 0 noise 0 101.59 0 -0.1 0.14
951768133 12.0295 30 0 0.1 12.03 4.19 0.99 0.34 52.9 341 2.49 335 850138212 0.22 0.97 18.21 190.64 0.17 0.1 0.11 0 good 0 97.13 0 -0.02 0.01
951768139 4.95733 80 -0.69 0.11 4.96 4.35 0.95 0.8 40.97 342 1.87 336 850138212 0.31 0.99 35.08 163.45 0.09 0.26 0.02 0 good 1.92 63.35 0 -0 0.06
951768144 3.58524 20 0 0.07 3.59 5.36 1 0.26 74.46 343 3.01 337 850138214 0.37 0.9 41.05 227.49 0.29 0.08 0.5 0 noise nan 97.07 0 -0.06 0.25
951768149 3.98442 40 -0.34 0.13 3.98 4.04 0.99 0.87 50.92 345 2.07 338 850138214 0.37 0.98 50.86 211.84 0.13 0.19 0 0 noise 0 71.27 0 -0.02 0.09
951768154 5.94749 40 -2.06 0.24 5.95 4.74 0.95 0.76 88.99 346 3.42 339 850138216 0.38 0.99 36.11 116.07 0.26 0.21 0.01 0 good 1.37 78.34 0 -0.02 0.52
951768160 2.84969 60 -0.69 0.15 2.85 2.99 0.8 0.74 50.47 347 1.98 340 850138216 0.39 0.99 59.98 250.53 0.14 0.23 0.01 0.01 good 1.03 46.43 0.02 -0.01 0.27
951768165 5.99213 40 -0.34 0.12 5.99 2.65 0.86 0.8 42.2 348 1.8 341 850138214 0.39 0.9 25.23 150.42 0.11 0.22 0 0.01 noise 0 63.11 0.01 -0.01 0.01
951768170 4.00664 50 -0.34 0.16 4.01 4.91 0.88 0.8 56.55 349 2.05 342 850138214 0.6 0.97 23.17 61.6 0.11 0.19 0 0.01 good -1.37 82.57 0.01 -0.01 0
951768177 2.6113 70 0.69 0.12 2.61 4.97 0.89 0.62 63.38 350 2.55 343 850138222 0.48 0.99 11.56 163.43 0.19 0.18 0.01 0 good 1.24 61.78 0 -0.04 0.37
951768183 5.32107 60 1.51 0.05 5.32 3.82 0.98 0.85 23.83 351 0.82 344 850138224 0.72 0.99 28.91 268.31 0.03 0.41 0.5 0 good 0.34 82.57 0 -0.01 0.03
951768188 3.62843 120 0.78 0.08 3.63 3.44 0.89 0.65 43.1 352 0.99 345 850138234 0.35 0.99 46.44 481.61 0.06 0.3 0.15 0 good 2.41 62.08 0.01 -0.01 0.18
951768196 1.16005 40 -1.37 0.07 1.16 2.25 0.7 0.6 91.52 353 2.84 346 850138224 0.41 0.99 12.04 240.61 0.29 0.19 0.48 0 good 1.37 38.42 0.02 -0.03 0.2
951768201 4.48178 40 nan 0.07 4.48 3.82 0.96 0.25 59.24 354 2.16 347 850138224 0.47 0.99 16.89 347.72 0.25 0.11 0.19 0 noise -1.17 80.22 0 -0.04 0.06
951768209 1.65337 100 0.69 0.19 1.65 4.79 0.94 0.76 75.97 355 1.8 348 850138224 0.59 0.98 26.25 142.83 0.13 0.14 0 0 good 1.57 76.84 0 -0.03 0
951768215 2.43232 50 nan 0.13 2.43 3.04 0.75 0.6 58.67 356 1.35 349 850138224 0.86 0.99 42.78 251.36 0.11 0.25 0.13 0 good 0.41 46.33 0.01 -0.02 0.33
951768222 38.6918 90 0.27 0.18 38.69 7.69 1 0.27 131.16 357 4.61 350 850138226 0.67 0.99 51.34 68.83 0.6 0.21 0 0 good 0.45 179.21 0 -0.12 0
951768228 1.4528 90 0 0.22 1.45 5.38 0.82 0.71 101.18 358 2.72 351 850138228 0.49 0.83 28.24 64.54 0.23 0.18 0 0 good 1.63 53.24 0 -0.03 0.02
951768234 0.04402 60 0.34 nan 0.04 4.46 0 0.59 111.33 359 3.28 352 850138230 0.47 0.77 4.04 8.18 0.34 0.14 0.07 0 good 0.69 25.58 0.01 -0.09 0
951768239 2.24094 80 0 0.09 2.24 4.54 0.91 0.63 60.27 360 1.82 353 850138230 0.3 0.92 24.32 188.31 0.17 0.19 0.16 0 good 1.33 61.61 0 -0.02 0.29
951768247 6.3691 90 0.96 0.08 6.37 4.4 0.97 0.63 74.66 361 2.72 354 850138232 0.45 0.99 40.39 153.31 0.2 0.22 0 0 good 2.61 87.52 0 -0.02 0.01
951768252 0.95854 60 -0.34 0.2 0.96 5.39 0.92 0.66 98.62 362 3.09 355 850138232 0.4 0.97 39.32 97.04 0.34 0.16 0 0 good 0.96 51.2 0 -0.04 0.34
951768258 2.92234 120 0.89 0.07 2.92 2.75 0.89 0.59 42.02 363 1.63 356 850138232 0.51 0.99 25.52 356.29 0.11 0.27 0.29 0 good 2.44 58.17 0 -0.01 0.31
951768266 1.54962 70 0.34 0.11 1.55 3.74 0.96 0.63 62.72 364 2.29 357 850138232 0.48 0.99 40.65 234.69 0.18 0.18 0 0 good 0.76 72.49 0 -0.03 0
951768272 0.11047 80 -0 nan 0.11 4.76 0.37 0.69 108.48 365 3.15 358 850138238 0.4 0.9 21.58 55.55 0.34 0.16 0.01 0 good 0.48 45.02 0 -0.05 0
951768278 9.61519 60 -0.34 0.26 9.62 5.53 0.99 0.26 136.17 366 4.23 359 850138238 0.58 0.99 55.36 83.51 0.61 0.14 0 0 good -0.07 80.31 0 -0.12 0.01
951768285 3.60332 110 0.07 0.11 3.6 3.7 0.8 0.58 57.68 367 1.89 360 850138238 0.62 0.99 33.42 243.03 0.16 0.22 0.07 0 good 1.91 47.62 0.02 -0.03 0.33
951768291 2.06661 100 0.55 0.05 2.07 3.15 0.58 0.58 50.41 368 1.47 361 850138238 0.87 0.95 37.9 267.74 0.14 0.27 0.5 0 good 0.75 35.92 0.03 -0.04 0.42
951768298 7.5058 90 0.55 0.09 7.51 4.16 0.97 0.37 36.41 369 1.5 362 850138240 0.52 0.99 19.84 213.53 0.15 0.18 0.05 0 good 0.69 78.51 0 -0.02 0.07
951768307 3.44108 90 0.69 0.09 3.44 4.25 0.9 0.56 56.87 370 2.35 363 850138240 0.5 0.99 33.76 269.32 0.17 0.22 0.17 0 good 0.96 45.51 0.03 -0.03 0.22
951768313 2.51974 130 0.94 0.06 2.52 3.14 0.81 0.29 49.78 371 1.4 364 850138238 0.78 0.91 30.73 332.36 0.22 0.16 0.5 0 noise 0 44.65 0.02 -0.06 2.11
951768318 11.362 60 -0.34 0.08 11.36 3.76 0.96 0.44 59.59 372 2.33 365 850138246 0.47 0.99 39.23 80.89 0.21 0.18 0.01 0.01 good 0.69 76.75 0 -0.02 0.09
951768327 1.25057 100 0.08 0.09 1.25 3.26 0.69 0.73 49.96 373 1.82 366 850138246 0.46 0.99 29.45 346.08 0.13 0.23 0.06 0 good 1.03 40.75 0.02 -0.01 0.5
951768332 18.085 110 0 0.11 18.09 3.71 0.98 0.32 57.36 374 2.41 367 850138248 0.43 0.99 19.84 111.74 0.24 0.19 0.35 0.02 good 0.61 104.15 0 -0.03 0.06
951768340 2.44038 90 -0.55 0.1 2.44 3.34 0.77 0.54 65.7 375 2.2 368 850138248 0.36 0.99 38.97 240.71 0.22 0.19 0.03 0 good 1.03 32.32 0.05 -0.02 0.16
951768345 4.23646 40 0 0.17 4.24 3.54 0.98 0.21 105.62 376 0.74 369 850138248 0.3 0.99 35.36 277.45 0.08 0.11 0 0 good 0 55.6 0.01 -0.03 0.01
951768352 1.72974 110 -0.14 0.06 1.73 3.73 0.79 0.47 49.35 377 1.65 370 850138252 0.39 0.99 24.23 295.49 0.16 0.21 0.5 0 good -0.66 46.26 0.01 -0.02 0.17
951768356 3.20248 170 0.4 0.07 3.2 2.69 0.75 0.63 54.05 378 1.17 371 850138258 0.68 0.99 22.48 427.4 0.11 0.32 0.5 0 noise 0.69 43.34 0.02 -0.03 0.5
951768363 1.26452 80 0.27 0.14 1.26 3.62 0.97 0.7 150.05 379 3.27 372 850138258 0.44 0.99 39.89 164.78 0.45 0.18 0 0 good 1.17 82.56 0 -0.06 0.27
951768369 4.01356 100 -0.37 0.08 4.01 3.36 0.92 0.62 46.8 380 1.66 373 850138254 0.4 0.99 33.87 278.33 0.14 0.21 0.4 0 good 1.3 59.85 0 -0.02 0.1
951768374 10.5394 90 1.03 0.19 10.54 4.31 0.97 0.54 97.88 381 3.6 374 850138254 0.57 0.99 37.27 76.52 0.27 0.26 0 0 good 0.44 81.65 0 -0.06 0
951768382 11.6807 40 0 0.16 11.68 4.37 0.99 0.48 74.33 382 2.02 375 850138256 0.18 0.99 22.96 219.38 0.23 0.23 0.5 0 good 2.4 82.87 0 -0 0.01
951768390 27.369 70 -0.34 0.15 27.37 9.19 1 0.23 204.25 383 5.05 376 850138258 0.62 0.99 49.26 74.52 0.92 0.12 0 0 good 0 221.47 0 -0.22 0
951768402 7.5028 60 0.14 0.1 7.5 3.6 0.99 0.65 50.99 384 1.29 377 850138262 0.58 0.99 37.42 123.26 0.14 0.27 0 0 good 2.4 78.13 0 -0.05 0.01
951768408 11.9073 110 0.27 0.27 11.91 6.66 1 0.51 231.84 385 5.13 378 850138260 0.54 0.99 53.8 133.8 0.63 0.19 0 0 good 1.1 131.73 0 -0.13 0
951768415 1.64232 110 0.82 0.15 1.64 4.53 0.94 0.65 124.38 386 2.54 379 850138260 0.4 0.96 46.53 209.42 0.38 0.16 0 0 good 1.73 68.33 0 -0.05 0
951768421 11.2489 150 0.69 0.11 11.25 3.01 0.96 0.58 68.19 388 1.64 380 850138262 0.48 0.99 39.42 163.66 0.18 0.27 0.27 0 good 1.02 80.55 0 -0.03 0.11
951768427 5.18322 70 0 0.21 5.18 4.12 0.97 0.59 146.55 389 3.12 381 850138262 0.49 0.99 45.7 93.36 0.41 0.22 0 0 good 0.34 65.12 0 -0.08 0.02
951768434 10.6732 90 0.34 0.13 10.67 6.41 0.99 0.56 212.66 390 4.57 382 850138262 0.49 0.99 48.21 113.7 0.56 0.22 0 0 good 0.66 100.02 0 -0.1 0
951768441 23.9354 90 0.69 0.15 23.94 2.97 0.94 0.58 113.53 391 2.16 383 850138264 0.55 0.99 46.27 120.36 0.28 0.23 0.07 0.01 good 0.89 109.46 0.01 -0.04 0.23
951768446 14.5898 50 0.34 0.27 14.59 4.75 1 0.71 283.84 392 4.82 384 850138264 0.36 0.99 39.6 61.89 0.81 0.16 0 0 good 1.37 73.65 0 -0.1 0
951768451 11.3477 100 0.76 0.11 11.35 2.61 0.84 0.55 126.84 394 2.32 385 850138264 0.66 0.99 52.79 132.17 0.33 0.27 0.01 0.01 good 0.71 51.79 0.02 -0.06 0.07
951768457 9.15917 110 -0.41 0.12 9.16 3.62 0.97 0.62 88.38 395 2.11 386 850138266 0.34 0.99 38.89 148.56 0.22 0.23 0.01 0 good 1 83.74 0 -0.04 0.03
951768462 3.18564 150 0.49 0.08 3.19 2.56 0.89 0.63 74.29 396 1.35 387 850138264 0.65 0.99 47.5 320.97 0.18 0.25 0.5 0 good 0.7 56.02 0 -0.03 0.12
951768467 1.92143 90 0.34 0.22 1.92 5.98 0.97 0.63 177.05 397 3.65 388 850138268 0.46 0.99 44.78 143.72 0.45 0.22 0 0 good 0.55 66.03 0 -0.08 0
951768473 8.20703 100 0.41 0.1 8.21 3.15 0.93 0.6 104.16 398 2.42 389 850138270 0.47 0.99 44.27 150.8 0.26 0.23 0.04 0 good 0.48 60.86 0 -0.04 0.11
951768480 5.17423 100 -0.89 0.07 5.17 3.72 0.92 0.29 83.66 399 1.89 390 850138270 0.52 0.99 33.32 228.75 0.38 0.21 0.07 0 good 0.66 51.54 0.01 -0.07 0.04
951768487 0.31145 90 0.55 nan 0.31 3.46 0.14 0.67 76.47 400 1.71 391 850138270 0.5 0.99 46.11 527.28 0.18 0.27 0.15 0 good 0.41 32.81 0.01 -0.03 0
951768495 16.5755 90 0.34 0.12 16.58 4.94 0.98 0.65 187.4 401 3.96 392 850138272 0.45 0.99 43.23 94.78 0.45 0.22 0 0 good 1.03 65.87 0.01 -0.07 0.01
951768500 11.2425 70 1.03 0.13 11.24 5.14 0.98 0.23 158.18 402 2.91 393 850138272 0.66 0.99 35.2 138.62 0.72 0.14 0 0 good 0 68.25 0 -0.18 0.02
951768506 0.13651 130 0.78 -0.01 0.14 1.92 0 0.67 84.61 403 1.43 394 850138272 0.68 0.97 49.12 187.35 0.17 0.33 0.36 0 good 1.03 24.72 0.04 -0.04 0
951768511 6.84621 100 0.07 0.1 6.85 3.94 0.95 0.8 133.13 404 2.53 395 850138272 0.33 0.99 50.16 222.39 0.36 0.22 0 0 good 1.03 61.39 0 -0.03 0.23
951768519 0.21856 100 0.31 nan 0.22 3.55 0.15 0.7 77.19 405 2.07 396 850138274 0.34 0.98 41.48 292.64 0.2 0.26 0.09 0 good 0.82 40.24 0 -0.02 0
951768524 4.24338 100 1.03 0.13 4.24 4.11 0.97 0.62 89.6 406 1.93 397 850138270 0.54 0.99 28.3 182.78 0.21 0.25 0.03 0 good 0.34 53.49 0 -0.04 0.35
951768530 2.67815 130 0.86 0.09 2.68 3.17 0.84 0.62 68.81 407 1.87 398 850138276 0.48 0.99 37.63 260.5 0.18 0.25 0.49 0 good 0.61 58.71 0 -0.03 0.09
951768538 4.26591 150 0.81 0.04 4.27 2.69 0.83 0.6 47.3 408 1.12 399 850138276 0.5 0.99 52.01 334.71 0.1 0.3 0.32 0 good 0.77 50.34 0.01 -0.02 0.66
951768544 2.18772 50 0.34 0.22 2.19 4.8 0.97 0.76 126.84 409 3.19 400 850138276 0.31 0.84 11.68 66.98 0.4 0.16 0 0 good 0.69 77.91 0 -0.04 0.01
951768550 2.01825 60 0.69 0.09 2.02 5.4 0.99 0.73 146.88 410 4.01 401 850138278 0.36 0.99 35.52 96.93 0.39 0.19 0 0 good 0.69 70.97 0 -0.07 0
951768557 7.48875 60 -0.69 0.15 7.49 3.75 0.97 0.36 107.66 411 2.79 402 850138278 0.48 0.99 37.44 113.64 0.44 0.16 0 0 good -0.14 72.89 0 -0.09 0.01
951768563 1.62082 60 0.34 0.11 1.62 5.8 0.96 0.73 170.18 412 3.74 403 850138278 0.41 0.99 40.57 113.95 0.48 0.19 0 0 good 0.41 70.71 0 -0.06 0
951768568 7.46457 70 -0.69 0.09 7.46 3.59 0.94 0.3 74.52 413 1.99 404 850138278 0.42 0.99 33.29 217.09 0.34 0.16 0.34 0 good -0.48 64.16 0 -0.06 0.13
951768575 1.83111 60 0.69 0.13 1.83 5.4 0.99 0.67 203.62 414 5.12 405 850138280 0.43 0.99 40.34 88.38 0.56 0.19 0 0 good 0.89 94.58 0 -0.08 0
951768581 4.42153 120 0.06 0.12 4.42 3.04 0.94 0.67 84.11 415 2.19 406 850138280 0.56 0.99 25.35 223.66 0.2 0.26 0.06 0 good 1.01 65.16 0 -0.04 0.25
951768586 2.11725 60 0.27 0.08 2.12 3.56 0.9 1 87.43 416 2.2 407 850138280 0.25 0.99 30.08 288.52 0.28 0.18 0.02 0 good 2.06 61.93 0 -0.02 0.11
951768593 2.39016 80 0.34 0.12 2.39 4.36 0.96 0.71 104.4 417 2.89 408 850138282 0.43 0.99 36.7 183.21 0.28 0.21 0.01 0 good 0.96 67.75 0 -0.03 0.31
951768598 1.75857 70 -0.07 0.06 1.76 4.99 0.94 0.62 141.52 418 3.51 409 850138282 0.5 0.99 36.86 129.05 0.4 0.18 0 0 good 0.62 64.8 0 -0.07 0.03
951768604 6.47378 110 -4.4 0.06 6.47 3.23 0.96 0.23 57.31 419 1.75 410 850138284 0.48 0.99 19.85 312.87 0.26 0.11 0.47 0.01 good 2.92 72.41 0 -0.07 0.06
951768611 0.82968 40 1.37 0.29 0.83 5.53 0.99 0.15 241.99 420 5.06 411 850138284 1.97 0.73 27.78 249.16 0.88 0.11 0 0 good 0.34 105.98 0 -0.25 0
951768616 1.5769 70 0.34 0.11 1.58 5.23 0.94 0.85 123.63 421 3.26 412 850138284 0.29 0.99 35.19 120.54 0.37 0.18 0 0 good 0.69 66.96 0 -0.03 0
951768621 3.24547 80 0.2 0.13 3.25 3.64 0.78 0.62 96.42 422 2.5 413 850138286 0.49 0.99 37.05 172.85 0.28 0.19 0.04 0 good 0.69 50.36 0.01 -0.05 0.53
951768627 11.0219 50 -0.34 0.14 11.02 5.34 1 0.4 106.41 423 3.08 414 850138286 0.57 0.99 38.52 82.75 0.4 0.18 0 0 good -0.34 104.77 0 -0.07 0
951768632 4.57457 60 -0.27 0.07 4.57 3.5 0.82 0.62 92.98 424 2.26 415 850138286 0.43 0.99 35.39 138.14 0.29 0.18 0.02 0.01 good 0.69 52.32 0.01 -0.05 0.82
951768637 2.74026 160 1.54 0.1 2.74 2.65 0.29 0.36 68.56 425 1.56 416 850138288 0.39 0.99 32.68 335.81 0.27 0.22 0.5 0.01 noise 0.69 32.34 0.1 -0.03 2.55
951768643 1.4684 50 0.34 0.12 1.47 4.68 0.83 0.63 91.57 426 2.58 417 850138288 0.42 0.99 15.19 154.16 0.25 0.21 0.03 0 good 1.03 53.52 0 -0.03 0.29
951768649 5.50615 160 -0.59 0.04 5.51 3.62 0.88 0.29 85.4 427 2.2 418 850138288 0.48 0.99 29.6 187.55 0.39 0.21 0.07 0.01 good 0.38 49.16 0.02 -0.06 0.18
951768655 2.28073 70 0.14 0.08 2.28 3.25 0.85 0.66 68.89 428 1.91 419 850138288 0.38 0.99 47.34 212.72 0.19 0.23 0.5 0 good 1.03 46.33 0.01 -0.02 0.66
951768660 0.7403 40 0.34 0.19 0.74 6.5 0.92 0.6 148.56 429 3.4 420 850138290 0.43 0.99 34.1 137.37 0.44 0.18 0 0 good 1.37 57.65 0 -0.07 0.07
951768668 2.53855 70 -0.07 0.05 2.54 3.04 0.87 0.62 77.47 430 2.07 421 850138290 0.42 0.99 32.07 221.54 0.2 0.25 0.2 0 good 1.03 49.99 0.01 -0.04 0.72
951768673 1.92969 30 0.69 0.13 1.93 4.5 0.95 0.65 123.47 431 2.98 422 850138294 0.4 0.99 39.08 131.79 0.38 0.16 0 0 good nan 57.96 0 -0.06 0.08
951768681 0.49353 60 0.34 0.08 0.49 6.11 0.75 0.67 97.9 432 2.65 423 850138292 0.39 0.99 9.37 128.55 0.29 0.18 0.02 0 good 1.3 50.42 0 -0.05 1.11
951768686 3.26159 160 0.41 0.07 3.26 1.89 0.29 0.36 59 433 1.3 424 850138294 0.39 0.99 64.72 503.6 0.23 0.22 0.49 0.01 noise 0.69 31.07 0.09 -0.07 2.01
951768693 2.85889 80 0.27 0.07 2.86 3.9 0.87 0.45 68.35 434 1.78 425 850138294 0.46 0.99 23.04 288.14 0.24 0.23 0.5 0 good 0.69 50.69 0.01 -0.03 0.73
951768699 4.46896 80 -1.99 0.06 4.47 3.92 0.9 0.19 75.11 435 2.05 426 850138294 0.49 0.98 36.04 356.14 0.32 0.1 0.5 0 good 6.87 55.12 0.01 -0.1 0.17
951768705 4.19585 170 0.27 0.06 4.2 3.09 0.68 0.23 53.72 436 1.49 427 850138296 0.58 0.98 45.67 471.72 0.24 0.15 0.5 0.02 good 1.87 46.3 0.02 -0.08 1.49
951768712 4.65549 110 -0.15 0.1 4.66 4.29 0.96 0.52 56.86 437 1.83 428 850138296 0.65 0.99 35.96 186.21 0.21 0.19 0.42 0.01 good 2.4 77.17 0 -0.04 0.07
951768717 1.42169 50 1.03 0.13 1.42 4.49 0.71 0.63 79.13 438 2.19 429 850138296 0.42 0.99 15.71 280.98 0.26 0.18 0.16 0 good 0.69 43.81 0.01 -0.04 0.9
951768723 5.12256 110 0.14 0.09 5.12 4.59 0.92 0.19 107.81 439 2.65 430 850138296 0.45 0.99 25.54 235.18 0.46 0.14 0.05 0 good -0.05 52.05 0.01 -0.14 0.57
951768729 1.35205 170 0.46 0.01 1.35 1.77 0.11 0.33 35.4 440 0.85 431 850138294 0.43 0.97 46.81 541.76 0.14 0.21 0.5 0.01 noise 3.97 26.55 0.15 -0.05 2.29
951768735 0.81573 50 1.37 nan 0.82 5.27 0.91 0.56 69.19 441 2.04 432 850138300 0.29 0.99 16.35 205.03 0.23 0.21 0.02 0 good 0.69 50.48 0 -0.03 0.41
951768739 1.94953 80 0.41 0.09 1.95 3.84 0.72 0.71 62.21 442 1.7 433 850138300 0.26 0.99 26.84 344.06 0.18 0.22 0.3 0 good 1.44 37.76 0.03 -0.02 4.51
951768745 2.27897 170 0.39 0.02 2.28 1.81 0.2 0.37 34.87 443 0.9 434 850138296 0.42 0.99 54.8 678.05 0.12 0.23 0.5 0.01 noise 3.64 31.46 0.09 -0.06 1.66
951768749 2.02352 90 0.34 0.08 2.02 3.93 0.78 0.54 77.89 444 2.09 435 850138302 0.31 0.99 14.68 325.12 0.26 0.22 0.17 0 good 0.76 40.59 0.03 -0.03 2
951768754 1.3661 50 nan 0.01 1.37 3.19 0.73 0.54 66.69 445 1.78 436 850138302 0.26 0.99 40.27 249.64 0.26 0.14 0.11 0 good 0.96 39.58 0.02 -0.03 1.1
951768760 4.04994 170 1.02 0.03 4.05 2 0.35 1.18 43.94 446 1.08 437 850138294 0.24 0.99 24.89 420.36 0.09 0.45 0.5 0.02 noise 0.66 33.46 0.12 -0.01 1.41
951768766 8.87438 110 -0.77 0.1 8.87 3.63 0.99 0.47 54.19 447 1.68 438 850138304 0.62 0.99 29.51 198.67 0.18 0.19 0.08 0.02 good 1.55 76.71 0 -0.03 0.05
951768771 8.05575 90 0 0.18 8.06 6.55 0.99 0.25 125.46 448 3.3 439 850138304 0.58 0.99 35.39 184.91 0.57 0.14 0 0 noise -0.28 87.41 0 -0.12 0
951768776 0.03441 60 0.34 nan 0.03 6.64 0.22 0.62 173.28 449 4.04 440 850138308 0.41 0.66 3.25 2.55 0.55 0.16 0.02 0 good 0.89 42.7 0 -0.07 0
951768782 0.1641 70 0.34 nan 0.16 5.15 0.44 0.63 85.75 450 2.51 441 850138310 0.44 0.99 20.46 106.86 0.24 0.25 0 0 good 0.76 36.54 0 -0.03 0
951768786 3.67638 170 0.63 0.05 3.68 2.85 0.45 0.36 54.22 451 1.67 442 850138310 0.37 0.99 50.61 364.73 0.21 0.3 0.29 0.02 noise 0.27 35.31 0.08 -0.04 0.9
951768793 4.23739 150 1.2 0.03 4.24 2.94 0.6 0.3 43.5 452 1.31 443 850138302 0.35 0.99 23.89 400.44 0.19 0.65 0.5 0.02 good 0.15 43.61 0.04 -0.04 0.27
951768797 0.88393 70 0.34 0.2 0.88 6.73 0.93 0.62 134.03 453 3.24 444 850138312 0.39 0.99 25.27 181.32 0.39 0.18 0 0 good 1.1 60.45 0 -0.06 0.25
951768802 0.00651 90 0 nan 0.01 7.09 nan 0.69 147.07 454 3.93 445 850138314 0.41 0.42 nan 0 0.45 0.19 0 0 good 1.51 77.18 0 -0.09 0
951768807 2.17615 130 1.13 0.05 2.18 2.32 0.58 0.69 52.38 455 1.39 446 850138312 0.42 0.99 66.19 392.72 0.13 0.29 0.48 0 good 0.83 29.88 0.16 -0.03 1.32
951768810 2.27835 170 -2.68 0.03 2.28 1.99 0.25 1.1 33.01 456 0.87 447 850138302 0.69 0.99 49.62 755 0 0.99 0.5 0.02 noise -0.1 31.2 0.11 -0.02 0.78
951768815 2.70812 110 0.07 0.06 2.71 3.96 0.88 0.67 51.41 457 1.55 448 850138318 0.4 0.99 32.76 376.44 0.13 0.26 0.29 0 good 1.51 44.65 0.03 -0.01 1.89
951768820 5.31446 170 -0.98 0.05 5.31 2.8 0.72 0.3 46.06 458 1.2 449 850138304 0.4 0.99 34.72 460.37 0.2 0.21 0.49 0.01 noise 0.57 44.02 0.06 -0.04 0.19
951768823 6.52535 140 0.2 0.11 6.53 3.14 0.88 0.37 46.54 459 1.62 450 850138320 0.58 0.99 37.82 241.87 0.18 0.18 0.17 0.02 good 1.5 55.94 0.03 -0.03 0.22
951768830 10.9098 110 0.71 0.13 10.91 4.17 0.96 0.32 53.53 460 1.98 451 850138320 0.8 0.99 42.67 222.25 0.22 0.16 0.04 0.01 good -0.2 72.12 0.01 -0.04 0.03
951768835 7.83947 140 0.61 0.03 7.84 3.19 0.86 0.45 35.41 461 1.32 452 850138324 0.24 0.99 36.49 335.55 0.12 0.21 0.14 0.03 good 1.59 61.65 0.02 -0.01 0.11
951768842 2.49308 90 1.17 0.08 2.49 3.17 0.77 0.65 59.66 462 1.86 453 850138320 0.46 0.99 61.24 313.89 0.15 0.25 0.03 0.01 good 1.17 37.94 0.07 -0.03 0.52
951768848 4.81886 150 0.85 0.02 4.82 1.34 0.39 1.17 30.13 463 0.88 454 850138320 0.45 0.99 80.01 484.93 0.05 0.54 0.5 0.03 noise 0.81 36.44 0.13 -0.02 0.71
951768854 3.75047 170 2.44 0.01 3.75 nan nan 1.61 14.81 464 0.3 455 850138312 0.27 0.99 120.78 994.12 0.01 1.13 0.5 0 noise 0.62 nan nan -0.03 0.52
951768861 0.24088 60 0.41 nan 0.24 10.23 0.98 0.7 233.33 465 6.15 456 850138326 0.49 0.94 21.61 53.11 0.6 0.16 0 0 good 0.69 179.34 0 -0.11 0
951768867 0.03813 60 -0.76 nan 0.04 7.41 0.53 0.66 156.97 466 4.51 457 850138324 0.41 0.67 10.44 6.78 0.43 0.19 0 0 good 0.69 60.94 0 -0.08 0
951768875 0.94707 130 0.52 0.05 0.95 2.65 0.62 0.58 57.7 467 1.62 458 850138322 0.5 0.99 35.06 272.95 0.15 0.27 0.5 0 good 0.63 34.59 0.06 -0.01 2.46
951768881 2.06258 80 -0.43 0.14 2.06 4.27 0.99 1.17 68.02 468 2.37 459 850138326 0.29 0.99 21.18 181.41 0.22 0.18 0.08 0 good 3.09 67.02 0 -0.01 0.12
951768888 2.90921 120 0.69 0.04 2.91 2.02 0.65 0.84 53.31 469 1.67 460 850138328 0.32 0.99 17.46 317.8 0.15 0.26 0.3 0.01 good 0.96 37.17 0.1 -0.01 1.08
951768894 9.16155 80 -0.21 0.12 9.16 4.26 0.99 0.49 56.89 470 2.16 461 850138328 0.66 0.99 35.84 127.15 0.15 0.22 0.02 0.02 good 0.82 80.4 0 -0.03 0.06
951768901 3.99186 120 2.29 0.09 3.99 4.41 0.96 0.32 56.78 471 2.02 462 850138330 0.8 0.99 33.87 268.04 0.22 0.19 0.03 0 good 0.41 64.59 0 -0.08 0.21
951768907 2.85765 70 0.14 0.11 2.86 4.35 0.93 0.81 84.97 472 2.41 463 850138332 0.22 0.99 40.67 269.42 0.23 0.19 0.02 0.01 good 0.62 60.22 0.01 -0.01 0.3
951768913 0.0712 70 -0.14 nan 0.07 5.2 0.64 0.7 131.77 473 3.8 464 850138332 0.4 0.95 20.48 28.64 0.37 0.21 0.05 0 good 1.37 42.11 0 -0.05 7.64
951768920 1.85539 100 0.16 0.03 1.86 3.87 0.92 0.62 50.71 474 1.81 465 850138334 0.65 0.99 43.35 593.03 0.13 0.25 0.38 0 good 1.03 44.64 0.04 -0.01 1.49
951768925 2.28806 80 1.79 0.1 2.29 4.25 0.96 0.27 50.27 475 1.72 466 850138336 0.87 0.99 28.61 509.05 0.22 0.22 0.5 0.01 good 0 65.91 0 -0.05 1.15
951768932 0.78329 70 1.1 0.01 0.78 2.91 0.64 0.66 61.53 476 1.99 467 850138336 0.58 0.99 19.18 270.77 0.16 0.25 0.24 0 noise 0.34 38.61 0.06 -0.02 3.98
951768937 0.08412 60 0.55 nan 0.08 4.74 0.56 0.73 54.03 477 2.05 468 850138340 0.71 0.76 18 37.71 0.14 0.22 0.1 0 good 0.69 46.71 0 -0.03 0
951768944 0.96981 60 -0.07 0.11 0.97 3.52 0.91 0.67 61.79 478 2.29 469 850138344 0.45 0.99 20.83 492.34 0.15 0.33 0.05 0.02 good 0 66.76 0.01 -0.01 0.62
951768950 0.37893 170 0.1 0.1 0.38 1.3 0.1 0.44 24.63 479 0.7 470 850138364 0.83 0.44 19.26 12.23 0.06 0.32 0.5 0.02 noise -0.13 10.9 0.44 -0.02 89.55
951768957 10.2835 100 0.02 0.05 10.28 2.12 0.98 0.7 20.3 480 1.03 471 850138394 0.65 0.99 23.72 471.43 0.03 0.55 0.28 0.39 noise 0.69 231.68 0.1 -0.01 1.86
951768969 6.83019 140 0.33 0.12 6.83 nan nan 1.04 23.25 481 1.17 472 850138376 0.38 0.99 62.26 667.32 0.02 0.77 0.5 0 noise -0.22 nan nan -0 1.29
951768974 1.00556 100 0.06 0.24 1.01 2.63 0.73 0.65 53.18 482 1.97 473 850138394 0.87 0.97 18.59 270.34 0.08 0.49 0 0.02 noise 0 19.75 0.2 -0.04 13.67
951768980 6.48257 40 nan 0.02 6.48 3.2 0.87 0.58 134.91 483 3.26 474 850137694 0.47 0.99 30.36 177.42 0.42 0.21 0 0.01 good 0.21 37.05 0.01 -0.05 0.08
951768986 8.03663 50 nan 0.13 8.04 3.02 0.97 0.55 81.73 484 1.62 475 850137696 0.39 0.99 26.5 202.22 0.27 0.22 0.04 0 good 0.14 67.28 0 -0.02 0.05
951768990 1.87875 70 -0.21 -0 1.88 4.27 0.89 0.56 52.51 485 1.75 476 850137708 0.64 0.99 28.69 313.93 0.18 0.16 0.17 0 good -0.21 63.19 0 -0.02 0
951768995 4.25578 80 -0.48 0.02 4.26 3.08 0.62 0.58 78.48 486 2.35 477 850137712 0.51 0.99 31.16 162.25 0.22 0.23 0.25 0 good 0.21 45.79 0.01 -0.03 0.11
951769002 0.03389 70 -0.34 nan 0.03 3.6 0 0.65 107.87 487 2.02 478 850137722 0.67 0.89 nan 0 0.25 0.32 0.35 0 good 0.69 34.66 0 -0.05 0
951769007 15.5288 80 -0.75 0.13 15.53 3.1 0.98 0.66 79.25 488 1.59 479 850137738 0.65 0.99 10.95 105.58 0.11 0.37 0.06 0.01 good -0.34 97.7 0 -0.03 0.03
951769012 1.77727 90 -0.51 0.01 1.78 2.94 0.76 0.7 70.49 489 1.73 480 850137738 0.66 0.99 14.38 322.27 0.11 0.34 0.19 0 good 1.72 50.17 0 -0.02 0.01
951769018 2.70678 70 0 0.07 2.71 3.07 0.94 0.65 92.67 490 2.15 481 850137742 0.39 0.99 19.41 310.68 0.27 0.19 0.18 0 good -0.14 59.01 0 -0.04 0.09
951769024 7.12573 90 -1.44 0.06 7.13 3.44 0.97 0.67 56.66 491 1.34 482 850137742 0.7 0.99 11.23 220.52 0.06 0.4 0.09 0 good -0.06 93.5 0 -0.03 0.05
951769029 11.3657 70 -0.34 0.14 11.37 4.7 1 0.58 119.28 492 2.66 483 850137740 0.35 0.99 2.11 53.43 0.32 0.23 0 0 good -0.21 113.34 0 -0.05 0.01
951769034 10.5122 70 -1.03 0.03 10.51 4.49 0.97 0.65 79.64 493 2.64 484 850137750 0.56 0.99 7.7 74.29 0.19 0.3 0 0 good 1.1 76.82 0 -0.04 0.07
951769041 1.54229 70 -1.1 0.12 1.54 5.73 0.84 0.6 134.36 494 4.06 485 850137756 0.55 0.99 9.26 127.17 0.34 0.27 0 0 good -0.27 45.81 0.01 -0.06 0
951769046 6.2699 70 -1.55 0.01 6.27 3.29 0.73 0.56 72.64 495 2.33 486 850137758 0.35 0.99 10.67 121.54 0.2 0.23 0.08 0.01 good 0.69 54.81 0.01 -0.02 0.23
951769054 2.17036 90 -0.48 0.05 2.17 3.5 0.76 0.63 67.11 496 1.71 487 850137780 0.5 0.99 18.21 295.25 0.14 0.29 0.5 0 good 0.06 47.88 0.01 -0.02 0.08
951769060 2.35905 80 -0.34 0.12 2.36 5.93 0.91 0.73 109.64 497 3.16 488 850137792 0.39 0.99 13.35 175.83 0.33 0.18 0.01 0 good 0.62 62.82 0 -0.03 0.03
951769068 3.05016 70 -0.21 0.09 3.05 5.24 0.95 0.69 78.62 498 2.6 489 850137792 0.52 0.99 17.89 247.51 0.22 0.19 0.01 0 good 1.03 72.1 0 -0.04 0.01
951769074 0.03823 90 -0.21 nan 0.04 4.42 0 0.7 79.92 499 2.44 490 850137792 0.57 0.93 nan 0 0.19 0.26 0.17 0 good 1.24 29.42 0 -0.02 0
951769081 14.6808 80 -0.76 0.02 14.68 4.22 0.91 0.59 87.46 500 3.07 491 850137796 0.54 0.99 14.59 93.57 0.23 0.29 0 0.01 good -0.21 69.43 0.01 -0.04 0.05
951769088 2.94218 70 -0.34 0.17 2.94 5.5 0.99 0.59 99.1 501 2.95 492 850137800 0.37 0.99 8 139.53 0.33 0.16 0 0 good 0.89 83.72 0 -0.03 0.02
951769094 7.31804 60 -1.03 0.01 7.32 3.36 0.97 0.56 74.9 502 2.24 493 850137816 0.53 0.99 7.47 131.29 0.22 0.34 0.15 0.01 good -1.37 81.69 0 -0.04 0.08
951769100 2.82582 70 -0.21 0.14 2.83 4.02 0.94 0.63 80.5 503 2.36 494 850137818 0.4 0.99 13.89 187.43 0.24 0.21 0.09 0 good 1.03 61.39 0 -0.04 0.11
951769106 7.54703 80 -1.84 0.09 7.55 3.56 0.98 0.58 64.7 504 2.07 495 850137818 0.35 0.99 15.27 127.52 0.2 0.22 0.18 0 good 0 85.78 0 -0.03 0.04
951769112 2.67371 50 -0.69 0.12 2.67 7.48 0.96 0.6 173.13 505 4.9 496 850137824 0.48 0.99 17.5 66.74 0.58 0.16 0 0 good 1.03 83.85 0 -0.1 0
951769119 6.08782 60 -0.69 0.07 6.09 4.35 0.9 0.59 85.94 506 2.24 497 850137816 0.54 0.99 26.29 104.13 0.22 0.22 0 0.01 good 0.21 72.12 0 -0.05 0.1
951769125 2.68911 70 -0.69 0.03 2.69 4.03 0.71 0.56 71.32 507 1.98 498 850137816 0.45 0.99 26.7 200.83 0.21 0.21 0.04 0 good 0 48.84 0.01 -0.03 0.12
951769131 1.97671 60 -0.48 0.07 1.98 3.16 0.88 0.52 65.93 508 2.27 499 850137828 0.38 0.99 12.95 222.71 0.21 0.23 0.1 0 good 1.03 50.52 0 -0.02 0.28
951769138 2.61677 40 0 0.18 2.62 8.86 0.96 0.49 139.9 509 3.25 500 850137832 0.44 0.99 9.87 122.88 0.33 0.18 0 0 good 0 105.95 0 -0.04 0.02
951769144 1.13215 40 0 0.15 1.13 5.55 0.94 0.6 72.96 510 2.62 501 850137838 0.5 0.99 8.18 221.05 0.21 0.21 0.07 0 good 1.37 56.72 0 -0.04 0.66
951769149 3.25725 30 -0.69 0.07 3.26 5.08 0.89 0.49 120.58 511 4.38 502 850137848 0.52 0.99 13.81 102.36 0.43 0.16 0 0 good 1.37 59.68 0 -0.08 0.04
951769156 1.14785 110 0 0.06 1.15 5.9 0.95 0.26 43.92 512 1.68 503 850137986 0.19 0.99 22.32 703.55 0.19 0.14 0.5 0 good -1.04 62.8 0 -0.02 0.53
951769162 0.04485 70 nan 0.11 0.04 3.16 0.15 0.47 75.93 513 0.56 504 850137986 0.5 0.82 15.21 0 0.08 0.22 0.5 0 good 4.29 23.7 0.1 -0 269.59
951769169 0.04433 120 -2.13 nan 0.04 2.72 0.52 0.33 45.3 514 0.48 505 850138002 0.55 0.71 66.48 0 0.17 0.14 0.03 0 good 4.92 24.72 0.08 -0.01 376.21
951769174 1.73439 110 0 0.06 1.73 3.76 0.97 0.62 47.7 515 1.17 506 850138006 0.09 0.83 39.88 319.59 0.14 0.22 0.49 0 noise 0.98 69.74 0 -0.01 0.15
951769182 0.13651 80 -1.24 nan 0.14 1.61 0.5 0.38 86.2 516 1.13 507 850138002 0.38 0.82 50.65 107.77 0.26 0.33 0.5 0 good 0.55 32.25 0.01 -0.01 6.24
951769187 1.45662 100 1.34 0.12 1.46 4.7 0.87 0.4 46.66 517 0.33 508 850138052 1.29 0.98 19.52 166.57 0.04 0.27 0.02 0 noise 3.43 49.22 0.01 -0.01 0.6
951769194 1.14785 10 nan -0 1.15 2.7 0.68 1.14 52.2 518 2.02 509 850138088 0.02 0.99 5.5 175.76 0.26 0.3 0.01 0.02 noise nan 43.31 0.04 -0 0.21
951769200 0.28438 10 nan -0.01 0.28 2.43 0.53 1.83 50.29 519 1.42 510 850138088 0.03 0.99 32.95 693.87 0.03 1.33 0.01 0 noise nan 40.71 0.02 -0.02 10.54
951769207 0.01054 20 3.09 nan 0.01 2.79 0.13 1.14 36.8 520 0.72 511 850138088 0.28 0.6 nan 0 0.05 1.88 0.28 0 noise nan 56.99 0 -0.01 0
951769213 0.0156 20 -0.94 nan 0.02 2.66 0 0.77 48.74 521 1.23 512 850138088 0.04 0.72 nan 0 0.02 1.39 0.5 0 noise nan 26.22 0.01 nan 0
951769220 0.00889 20 4.72 nan 0.01 nan nan 0.85 49.85 522 1.2 513 850138088 0.05 0.42 nan 0 0.03 1.5 0.33 0 noise nan nan nan nan 0
951769226 0.03348 10 nan nan 0.03 3.87 0.11 0.87 51.5 523 1.48 514 850138088 0 0.77 40.89 40.89 0.01 1.51 0.07 0 noise nan 33.11 0.01 nan 0
951769233 0.04309 90 -2.88 -0.07 0.04 5.32 0.67 0.65 119.7 524 3.9 515 850138130 0.34 0.48 8.01 19.81 0.23 0.36 0.12 0 good -1.19 42.74 0 -0.02 20.86
951769238 0.01932 60 -0.21 nan 0.02 5.09 0 0.74 153.11 525 3.06 516 850138136 0.37 0.56 35.05 0 0.47 0.29 0.03 0 noise -1.72 44.09 0 -0.05 0
951769246 0.14777 140 -1.52 nan 0.15 6.02 0.61 0.74 111.16 526 2.93 517 850138132 0.31 0.96 24.84 89.09 0.35 0.19 0.02 0 good -0.46 43.34 0 -0.04 10.64
951769251 2.34118 110 -1.65 0.09 2.34 3.1 0.79 0.74 75.44 527 2.41 518 850138132 0.3 0.99 55.59 218.74 0.22 0.22 0 0 good -0.69 47.58 0.01 -0.01 0.18
951769259 0.10148 130 -1.94 nan 0.1 4.01 0.44 0.76 130.56 528 3.67 519 850138132 0.27 0.92 36.96 32.27 0.41 0.18 0.02 0 good -0.27 26.15 0.02 -0.04 0
951769264 1.08802 120 -1.61 0.03 1.09 3.72 0.81 0.71 85.45 529 2.31 520 850138148 0.29 0.99 56.92 307.01 0.29 0.18 0.01 0 good 0.34 48.71 0 -0.02 0.2
951769272 0.02769 100 -1.72 nan 0.03 4.69 0 1.3 78.53 530 2.14 521 850138162 0.49 0.48 7.77 7.77 0.17 0.25 0.5 0 good -0.14 44.04 0 0 0
951769277 0.02108 100 -0.76 nan 0.02 4.09 0 0.74 67.46 531 1.06 522 850138164 0.27 0.78 nan 0 0.09 0.37 0.21 0 good 0.39 37.58 0 -0 0
951769284 0.45054 60 0.41 0.15 0.45 4.91 0.93 0.56 110.21 532 2.89 523 850138238 0.57 0.92 34.61 116.89 0.33 0.15 0.01 0 good 0.69 51.19 0 -0.07 3.24
951769289 0.28851 130 0.56 nan 0.29 2.6 0.09 0.56 89.22 533 1.95 524 850138270 0.59 0.99 54.32 479.42 0.2 0.32 0.07 0 good 0.54 29.52 0.02 -0.03 0.47
951769295 3.27275 80 0.34 0.07 3.27 4.8 0.93 0.66 90.76 534 2.3 525 850138270 0.4 0.99 30.46 213.04 0.27 0.21 0.03 0 good 0.55 62.7 0 -0.03 0.2
951769299 4.57933 120 0.07 0.03 4.58 2.44 0.78 0.59 82.43 535 1.82 526 850138272 0.46 0.99 40.81 237.44 0.21 0.22 0.14 0 good 1.45 47.36 0.01 -0.03 0.15
951769304 2.04729 90 0.34 0.1 2.05 4.64 0.93 0.91 93.34 536 2.38 527 850138274 0.26 0.99 37.67 207.74 0.27 0.25 0 0 good 0.76 59.69 0 -0.02 0.05
951769309 1.31185 100 0.55 0.1 1.31 4.87 0.76 0.67 149.35 537 2.99 528 850138278 0.41 0.99 34.54 189.6 0.3 0.22 0.01 0 good 0.62 40.98 0.01 -0.05 0.61
951769314 1.02519 80 0.34 0.04 1.03 4.08 0.69 0.69 95.83 538 2.35 529 850138276 0.47 0.99 32.88 271.46 0.26 0.21 0.01 0 good 0.62 44 0 -0.06 0.04
951769319 0.83041 70 -0.14 -0.01 0.83 4.22 0.62 0.65 72.79 539 1.99 530 850138288 0.44 0.99 19.41 335.1 0.19 0.25 0.02 0 good 0.69 45.06 0 -0.03 0.17
951769325 0.75714 70 -0.21 -0.01 0.76 4.56 0.67 0.66 70.93 540 1.96 531 850138292 0.39 0.99 22.48 373.25 0.22 0.21 0.04 0 good 0.96 46.28 0 -0.04 1.55
951769330 1.10104 100 -0.04 0.05 1.1 4.06 0.75 0.8 64.83 541 1.62 532 850138308 0.34 0.99 38.07 319.78 0.19 0.21 0.03 0 good 1.85 35.42 0.04 -0.02 0.99
951769334 0.07223 70 0.34 0.02 0.07 7.28 0.5 0.66 179.82 542 4.42 533 850138308 0.44 0.78 21.2 20.62 0.55 0.18 0.01 0 good 1.17 58.49 0 -0.1 0
951769339 0.3778 70 -0.34 0.19 0.38 7.96 0.91 0.65 130.73 543 3.54 534 850138310 0.41 0.99 17.69 120.93 0.39 0.21 0 0 good 0.62 62.65 0 -0.05 1.09
951769344 0.94873 120 -0 0.18 0.95 8.13 0.98 0.69 81.61 544 2.22 535 850138314 0.33 0.99 10.39 89.17 0.22 0.23 0 0 good 1.4 80.42 0 -0.04 0.3
951769351 0.25638 90 0 0.13 0.26 6.04 0.89 0.65 118.7 545 3.32 536 850138314 0.29 0.99 25.31 147.91 0.36 0.19 0 0 good 0.82 58.77 0 -0.02 1.18
951769355 0.05136 70 0.21 nan 0.05 9.08 0.54 0.66 179.36 546 3.79 537 850138322 0.48 0.65 9.45 2.84 0.39 0.19 0.06 0 good 0.48 66.96 0 -0.05 14.68
951769362 0.04464 120 0.91 nan 0.04 3.81 0 0.63 78.14 547 2.27 538 850138328 0.46 0.9 0 0 0.21 0.29 0 0 good 0.69 23.05 0.06 -0.02 0
951769365 0.03141 50 0.21 nan 0.03 6.67 0.58 0.67 110.2 548 3.71 539 850138340 0.54 0.69 2.11 1.75 0.31 0.18 0.05 0 good 1.37 46.83 0 -0.05 0
951769371 0.25679 40 -0.48 nan 0.26 3.83 0.74 0.69 106.22 549 3.46 540 850138344 0.41 0.99 16.03 122.59 0.3 0.21 0.01 0.01 good nan 38.65 0.04 -0.03 7.64
951769377 0.16978 100 -0.02 0.16 0.17 2.9 0.77 0.62 98.5 550 2.51 541 850138394 0.88 0.92 16.13 70.63 0.14 0.48 0.04 0 noise 0 11.85 0.44 -0.08 76.68
951769383 0.08019 50 0.14 nan 0.08 5.23 0.08 0.59 66.52 551 2.15 542 850137838 0.4 0.89 7.58 31.53 0.22 0.32 0.28 0 good -0.69 33.26 0 -0.02 6.02
951769390 0.21091 80 -1.72 0.13 0.21 2.51 0.79 0.34 78.02 552 1.65 543 850138000 0.52 0.58 30.2 28.27 0.27 0.21 0.04 0 good -0.21 38.46 0.01 -0.05 6.97
951769395 0.03947 30 nan nan 0.04 6.9 0.48 0.37 164.95 553 3.5 544 850137998 0.54 0.09 12.54 10.52 0.52 0.27 0.02 0 good -2.06 64.45 0 -0.11 0
951769401 0.16813 10 nan -0.06 0.17 1.66 0.29 2.13 50.26 554 1.36 545 850138088 0.02 0.99 15.84 129.79 0.02 1.1 0.09 0 noise nan 34.49 0.03 -0.09 0
951769406 0.0434 10 nan nan 0.04 1.86 0.02 1.84 51.19 555 1.38 546 850138088 0.01 0.73 8.13 8.33 0.06 1.25 0.06 0 noise nan 27.67 0.04 -0 0
951769412 0.05704 10 nan -0.04 0.06 3.93 0.62 2.69 49.89 556 1.95 547 850138088 0.04 0.97 nan 0 0 0.55 0.02 0 noise nan 45.39 0 -1.22 0
951769418 0.01963 20 -5.41 nan 0.02 2.84 0.07 0.7 33.42 557 0.74 548 850138088 0.02 0.69 nan 0 0.01 0.48 0.2 0 noise nan 32.49 0.01 -0 0
951769424 0.15046 80 0.14 nan 0.15 6.09 0.83 0.74 96.6 558 2.75 549 850138324 0.33 0.96 9.74 102.88 0.28 0.23 0.01 0 good 0.48 44.56 0 -0.03 3.42
951769429 0.03513 80 -0.27 nan 0.04 4.57 0.28 0.91 86.57 559 2.24 550 850138324 0.29 0.56 2.9 12.51 0.17 0.26 0.21 0 good 0.96 32.84 0.01 -0.02 0
951769435 0.07027 50 0.55 nan 0.07 5.79 0.75 0.76 89.44 560 3.22 551 850138340 0.52 0.84 10.99 6 0.26 0.18 0.02 0 good 2.06 49.43 0 -0.04 0
951769443 0.09135 120 -0.76 -0.03 0.09 2.81 0.29 0.54 36.41 561 0.42 552 850138002 0.56 0.83 46.92 35.27 0.1 0.34 0.5 0 good -1.09 39.13 0 -0.01 4.64
951769448 0.04681 120 -0.41 nan 0.05 1.26 0.05 0.52 43.77 562 0.37 553 850138002 0.63 0.67 50.01 171.84 0.07 0.54 0.5 0 good -1.04 28.56 0.01 0 0
951769456 0.04392 10 nan -0.02 0.04 2.39 0 2.25 52.53 563 1.89 554 850138088 0.01 0.49 5.94 15.68 0.01 0.43 0 0 noise nan 23.66 0.05 -0.05 0
951769462 0.00827 20 1.37 nan 0.01 3.07 0 0.03 46.58 564 1.23 555 850138088 0.05 0.45 nan 0 0.74 nan 0.01 0 noise nan 42.69 0 nan 0
951769470 0.07368 10 nan nan 0.07 2.39 0.28 2.69 52.28 565 2.18 556 850138088 0.02 0.98 29.05 0 -0 0.58 0.03 0 noise nan 32.27 0.01 -1.21 0
951769475 0.05043 10 nan nan 0.05 5.38 0.6 0.91 53.4 566 1.81 557 850138088 0.01 0.68 27.89 53.34 0 1.66 0 0 noise nan 48.17 0 nan 0
951769482 3.38115 70 -1.1 0.13 3.38 4.61 1 0.95 144.29 567 3.45 558 850138164 0.23 0.73 24.77 80.19 0.49 0.18 0 0 good 0 106.16 0 -0.03 0.01
951769487 0.26702 20 nan nan 0.27 5.75 0.7 0.49 66.07 568 2.74 559 850138192 4.09 0.94 46.69 458.99 0.24 0.18 0 0 noise -13.05 44.15 0 -0.01 1.09
951769493 0.40022 70 0.34 0.11 0.4 4.84 0.64 0.59 121.81 569 4.09 560 850138230 0.49 0.98 24.93 106.87 0.37 0.15 0.01 0 good 0.82 43.94 0 -0.08 0.24
951769500 0.06045 100 0.43 nan 0.06 3.55 0.12 0.7 88.87 570 2.54 561 850138322 0.49 0.76 15.94 24.1 0.25 0.23 0.04 0 good 0.69 24.25 0.06 -0.05 0
951769506 0.05539 10 nan nan 0.06 3.85 0.39 0.73 53.34 571 1.9 562 850138088 0.02 0.95 0 0 0.01 1.44 0.23 0 noise nan 44.05 0 nan 0
951769514 0.02098 10 nan nan 0.02 2.54 0 0.85 52.89 572 1.52 563 850138088 0.02 0.83 nan 0 0.02 1.44 0.5 0 noise nan 26.82 0.01 nan 0
951769521 0.0371 80 -1.06 0.17 0.04 7.39 0.44 0.76 153.31 573 3.41 564 850138136 0.24 0.66 13.12 20.6 0.48 0.19 0 0 noise -0.34 67.97 0 -0.04 0
951769527 0.01674 20 4.38 nan 0.02 2.47 0 0.03 40.36 574 0.99 565 850138088 0.02 0.7 nan 0 0.57 nan 0.48 0 noise nan 32.19 0.01 nan 0
951769538 0.01116 20 2.32 -0.11 0.01 2.31 0 0.04 46.86 575 1.27 566 850138088 0.03 0.65 nan 0 0.54 nan 0.5 0 noise nan 40.65 0 nan 0
951769546 0.14694 70 0.55 0.17 0.15 4.21 0.67 0.65 123.52 576 3.37 567 850138322 0.43 0.94 18.87 68.91 0.4 0.22 0.01 0 good 0.41 43.37 0 -0.05 5.38
951769554 0.07172 10 nan nan 0.07 4.79 0.52 0.73 53.68 577 1.95 568 850138088 0.01 0.94 25.47 15.19 0.01 1.5 0.07 0 noise nan 46.04 0 nan 0
951769645 1.43048 80 nan nan 1.43 7.02 1 0.3 22.03 0 2.94 0 850140490 0.32 0.99 34.88 587.35 0.45 0.15 0.5 0 good 4.15 56.25 0 -0.05 0.68
951769654 2.99788 50 1.37 0.12 3 5.28 0.97 0.33 88.37 1 2.23 1 850140498 0.79 0.99 35.56 656.21 0.27 0.16 0.13 0 good -0.21 50.4 0 -0.02 0.07
951769662 33.2358 90 -0.69 0.11 33.24 2.06 0.8 0.4 74.12 2 1.82 2 850140500 0.5 0.99 50.91 310.49 0.28 0.26 0.18 0.07 good 0.25 48.4 0.15 -0.05 0.05
951769668 19.8743 40 -1.37 0.06 19.87 3.02 0.88 0.27 75.58 3 1.85 3 850140500 0.18 0.99 51.45 715.11 0.3 0.11 0.3 0.01 good 0 42.17 0.08 -0.03 0.01
951769674 0.00413 100 -0.69 nan 0 4.05 nan 0.34 138.89 4 3.44 4 850140500 0.23 0.21 nan 0 0.48 0.11 0.5 0 noise 2.04 43.81 0 -0.01 0
951769681 3.13717 60 -0.34 0.14 3.14 3.77 0.96 0.29 120.4 5 2.75 5 850140504 0.36 0.99 39.51 271.88 0.54 0.19 0.01 0 good -0.27 56 0 -0.07 0.03
951769688 3.78963 50 -0.34 0.16 3.79 4.72 0.93 0.21 136.38 6 3.13 6 850140506 0.6 0.99 44.05 366.36 0.6 0.11 0.15 0 good 0.34 58.07 0 -0.18 0.03
951769694 30.0669 70 -0.34 0.1 30.07 5.18 1 0.51 107.02 7 2.61 7 850140506 0.49 0.99 40.96 271.77 0.33 0.21 0.2 0 good 0.41 103.06 0 -0.07 0
951769698 37.0382 80 -0.14 0.02 37.04 2.33 0.8 0.3 85.47 8 1.88 8 850140508 0.49 0.84 44.25 167.45 0.33 0.21 0.16 0.07 good -0.96 65.21 0.08 -0.05 0.02
951769706 2.10733 80 0 0.3 2.11 7.37 0.96 0.15 308.93 9 5.7 9 850140508 0.73 0.69 27.07 108.17 1.16 0.1 0 0 good 0.48 95.37 0 -0.44 0
951769711 1.39586 50 -0.34 0.11 1.4 7.59 1 0.19 126.13 10 2.8 10 850140510 1.87 0.86 59.08 596.53 0.5 0.11 0.5 0 good 0.34 99.45 0 -0.16 0.58
951769718 0.04795 110 0 nan 0.05 3.2 0 0.19 135.64 11 2.92 11 850140510 1.28 0.59 44 155.49 0.57 0.1 0.15 0 good -0.54 9.73 0.04 -0.22 0
951769724 1.20748 70 0 0.37 1.21 4.25 0.97 0.23 308.26 12 4.46 12 850140512 0.66 0.99 19.03 258.6 1.08 0.14 0 0 good -0.27 62.93 0 -0.16 0
951769730 1.56461 70 -0.14 0.26 1.56 4.8 0.97 0.23 285.44 13 3.41 13 850140516 0.59 0.99 34.98 189.92 0.82 0.11 0 0 good -0.21 67.19 0 -0.2 0
951769737 0.54086 40 0 0.19 0.54 3.42 0.86 0.26 196.19 14 3.48 14 850140514 3.52 0.89 52.25 996.34 0.79 0.12 0.5 0 good 0 29.77 0.03 -0.1 9.53
951769744 11.9715 90 0.07 0.12 11.97 4.97 0.99 0.3 133.05 15 2.95 15 850140514 0.63 0.77 14.6 85.4 0.55 0.21 0.5 0 good 0.34 90.49 0 -0.14 0.02
951769751 1.9887 90 -0.59 0.14 1.99 4.23 0.93 0.25 128.99 16 2.69 16 850140516 0.61 0.99 55.83 380.42 0.58 0.14 0.07 0 good -0.07 59.24 0 -0.13 0.06
951769758 1.55376 50 0 0.12 1.55 5.38 0.99 0.22 150.74 17 2.86 17 850140518 3.63 0.88 50.55 1053.47 0.6 0.11 0.5 0 good 0.34 106.68 0 -0.1 0.67
951769764 3.96613 30 0 0.13 3.97 5.08 0.99 0.19 162.67 18 2.65 18 850140522 0.28 0.99 18.34 188.69 0.65 0.11 0.5 0 good 0 90.06 0 -0.15 0.03
951769771 51.3402 60 -0.34 0.08 51.34 6.71 1 0.25 287.27 19 5.02 19 850140522 0.43 0.99 45.2 121.84 1.28 0.14 0 0 good 0.27 163.51 0 -0.24 0
951769776 1.74369 70 0 0.16 1.74 7.09 0.99 0.23 372.14 20 4.31 20 850140522 0.45 0.99 43.87 148.26 1.58 0.14 0 0 good 0.48 82.95 0 -0.3 0.01
951769784 0.36385 60 0.69 0.04 0.36 3.13 0.24 0.23 95.72 21 1.59 21 850140526 0.48 0.99 30.64 562.39 0.42 0.14 0.5 0 good 0.21 33.3 0.01 -0.07 0.59
951769790 32.9643 60 0.34 0.03 32.96 3.95 0.98 0.16 157.71 22 2.63 22 850140528 1.5 0.99 11.59 295.96 0.54 0.11 0.01 0.01 good 0.55 99.2 0 -0.18 0
951769797 1.20262 60 0 0.04 1.2 5.14 0.9 0.16 196.43 23 3.48 23 850140530 0.78 0.99 21.13 369.22 0.7 0.11 0.5 0 good 0.34 51.48 0 -0.31 1.85
951769803 25.6825 80 0.07 0.02 25.68 3.8 0.99 0.37 113.4 24 2.1 24 850140528 0.89 0.99 27.63 163.6 0.28 0.19 0.24 0 good 1.1 103.47 0 -0.03 0.01
951769808 45.8666 50 0.14 0.08 45.87 7.9 1 0.3 279.29 25 3.77 25 850140532 0.56 0.99 37.79 104.55 1.18 0.18 0 0 good 0 134.13 0 -0.24 0.03
951769813 0.51606 50 -0.34 0.03 0.52 3.79 0.41 0.21 385.86 26 4.77 26 850140532 0.59 0.99 43.24 212.93 1.71 0.11 0.01 0 good 0.69 35.8 0.01 -0.46 2.62
951769818 12.9885 50 -0.34 0.12 12.99 3.96 0.98 0.38 125.7 27 2.63 27 850140534 0.32 0.99 30.26 137.85 0.47 0.12 0.12 0 good 0.34 74.77 0 -0.05 0.01
951769822 0.05198 30 nan nan 0.05 11.33 0.33 0.41 235.73 28 4.93 28 850140536 0.89 0.47 12.04 33.44 0.55 0.22 0.01 0 good -1.03 130.95 0 -0.04 0
951769826 38.6449 70 0.27 0.13 38.65 4.6 0.98 0.22 172.98 29 3.3 29 850140540 0.45 0.99 35.27 104.91 0.76 0.12 0 0.01 good -0.14 81.63 0 -0.16 0.02
951769833 33.3518 80 -0.69 0.04 33.35 5.53 1 0.43 100.17 30 1.23 30 850140542 0.38 0.99 38.53 115.14 0.22 0.23 0.01 0 good -0.41 88.33 0 -0.03 0.01
951769839 0.30897 90 0 0.18 0.31 5.23 0.36 0.16 244.39 31 3.2 31 850140544 0.72 0.99 30.54 154.82 0.92 0.12 0.01 0 good -0.14 32.75 0.02 -0.35 62.07
951769846 2.36701 70 -0.62 0.03 2.37 4 0.92 0.27 59.24 32 1 32 850140546 0.36 0.99 31.9 421.17 0.21 0.14 0.46 0 noise -0.27 55.86 0 -0.04 0.12
951769857 6.66723 50 0.48 -0.03 6.67 3.14 0.99 0.21 109.27 33 1.21 33 850140548 1.59 0.99 45.47 747.24 0.27 0.11 0.5 0 good 0 64.95 0 -0.08 0
951769864 4.09944 60 0.48 0.1 4.1 4.98 0.95 0.14 163.51 34 2.87 34 850140548 0.9 0.95 58.64 926.91 0.45 0.08 0.2 0 noise 0.34 58.13 0 -0.31 0.32
951769870 1.66247 80 0.31 -0 1.66 3.47 0.75 0.15 139.63 35 1.77 35 850140548 0.68 0.6 33.48 229.3 0.37 0.1 0.5 0 good 0.69 45.05 0.01 -0.13 0.17
951769875 3.81971 50 0.14 0.05 3.82 4.13 0.9 0.14 145.79 36 2.28 36 850140548 0.66 0.57 20.21 417.96 0.4 0.11 0.23 0 good 0 51.13 0.01 -0.14 0.17
951769878 27.2155 130 -0.69 0.13 27.22 3.34 0.96 0.29 105.5 37 2.16 37 850140550 0.4 0.99 33.02 120.67 0.46 0.18 0.26 0.02 good 0.34 82.35 0 -0.06 0.01
951769883 2.62452 70 -0.21 0.08 2.62 3.68 0.5 0.23 155.18 38 2.76 38 850140550 0.73 0.99 33.49 284.23 0.71 0.15 0.02 0 good -0.34 30.07 0.04 -0.2 0.08
951769890 25.5366 40 -0.34 0.12 25.54 4.72 1 0.19 111.98 39 2.16 39 850140552 0.2 0.99 12.22 135.35 0.43 0.08 0.17 0 good 8.93 91.17 0 -0.1 0.01
951769898 25.2519 80 -0.41 0.1 25.25 4.95 0.97 0.34 156.18 40 3.01 40 850140552 0.56 0.99 34.35 103.15 0.47 0.22 0 0 good 0.07 73.6 0.01 -0.15 0.01
951769905 20.452 60 -0.34 0.07 20.45 4.85 0.99 0.36 124.59 41 2.07 41 850140552 0.22 0.99 36.01 122.31 0.47 0.14 0.05 0 good -0.07 69.25 0 -0.06 0
951769911 2.5649 110 -0.34 0.06 2.56 2.6 0.36 0.36 116.18 42 2.06 42 850140554 0.56 0.99 32.26 344.23 0.45 0.18 0.5 0 noise 0.48 27.81 0.06 -0.08 0.12
951769917 0.6165 70 0 0.12 0.62 4.2 0.35 0.21 181.19 43 2.54 43 850140556 0.59 0.99 19.65 454.62 0.78 0.14 0.5 0 good 0 27.58 0.02 -0.17 2.45
951769923 47.8529 60 -1.03 0.18 47.85 4.27 0.93 0.27 205.6 45 3.42 44 850140562 0.48 0.99 32.65 75.35 0.9 0.16 0.02 0.02 good 0 89.61 0.01 -0.17 0.01
951769930 6.53403 70 -0.41 0.08 6.53 3.05 0.64 0.22 153.85 46 2.17 45 850140562 0.61 0.99 29.17 177.72 0.68 0.14 0.14 0 good 0 36.27 0.04 -0.2 0.14
951769935 3.4045 60 0 0.06 3.4 2.54 0.26 0.33 188.26 48 2.88 46 850140562 0.42 0.99 40.44 243.87 0.79 0.16 0.5 0 noise 0.14 25.73 0.08 -0.12 0.13
951769941 33.4774 50 0 0.11 33.48 3.91 1 0.26 165.87 50 1.9 47 850140564 0.57 0.99 32.22 111.49 0.75 0.15 0.1 0 good 0.07 111.19 0 -0.16 0.01
951769948 39.7706 50 -1.03 0.03 39.77 5.99 1 0.36 390.49 51 4.27 48 850140566 0.5 0.99 40.7 114.14 1.46 0.18 0 0 good 0 81.18 0 -0.28 0
951769953 0.00682 120 0.55 nan 0.01 3.54 nan 0.36 292.89 52 2.12 49 850140566 0.31 0.43 nan 0 1.23 0.14 0.5 0 good -1.58 39.58 0 -0.12 0
951769959 8.49503 60 -0.69 0.08 8.5 4.94 0.99 0.18 183.45 53 2.58 50 850140574 0.57 0.99 28.55 138.5 0.69 0.1 0 0 good 0.21 85.05 0 -0.23 0.01
951769966 0.20957 90 -0.56 0.17 0.21 8.2 0.39 0.14 409.38 54 4.37 51 850140570 0.98 0.87 63.47 185.98 1.18 0.08 0 0 noise 0.34 79.41 0 -0.73 3.53
951769971 1.13907 50 -0.34 0.21 1.14 8.59 0.98 0.38 686.47 55 6.03 52 850140570 1.01 0.85 18.7 420.56 1.36 0.14 0 0 good 0.34 99.78 0 -0.04 0.48
951769978 35.3371 50 0 0.12 35.34 3.29 0.93 0.29 172.8 56 2.93 53 850140570 0.47 0.99 35.5 108.71 0.74 0.19 0.05 0.01 good 0.34 67.25 0.02 -0.12 0
951769985 10.3165 140 -0.02 0.13 10.32 3.54 0.97 0.19 199.07 57 2.59 54 850140578 0.56 0.99 48.37 185.05 0.85 0.11 0 0 good 0.61 57.85 0.01 -0.24 0.14
951769992 0.37335 50 0 nan 0.37 7.21 0.86 0.16 326.46 58 4.64 55 850140572 0.75 0.99 18.89 148.66 1.18 0.11 0 0 good 0 50.2 0 -0.5 0
951769999 2.20922 30 0 0.06 2.21 4.88 0.77 0.41 126.19 59 1.94 56 850140574 6.32 0.99 56.04 1434.91 0.43 0.1 0.39 0 noise -0.69 57.29 0 -0.02 0.13
951770005 5.12298 50 -0.34 0.03 5.12 5.18 0.93 0.22 133.38 60 2.21 57 850140574 2.11 0.94 24.52 555.66 0.57 0.12 0.5 0 good 0 83.17 0 -0.12 0.04
951770012 4.62014 20 0 0.09 4.62 3.81 0.85 0.21 183.16 61 2.61 58 850140578 0.21 0.96 11.45 155.04 0.72 0.1 0.5 0 noise nan 58.34 0 -0.12 0.08
951770018 13.4504 80 0 0.12 13.45 5.35 1 0.14 196.21 62 2.99 59 850140580 0.65 0.99 32.14 204.61 0.59 0.08 0 0 good 0.41 82.73 0 -0.3 0.01
951770024 9.66686 110 -0.08 0.11 9.67 4.53 0.89 0.33 161.83 63 2.33 60 850140584 0.3 0.99 37.95 185.78 0.66 0.19 0.5 0.01 good 0.16 59.27 0.01 -0.09 0.14
951770031 1.18785 70 0.21 -0.1 1.19 5.51 0.91 0.18 454.41 64 4.73 61 850140582 0.74 0.91 38.99 149.11 1.84 0.12 0 0 good 0.48 64.66 0 -0.64 1.29
951770036 41.438 90 -0.14 0.06 41.44 6.49 0.99 0.29 233.4 65 3 62 850140582 0.66 0.99 40.33 119.33 1.06 0.21 0 0 good 0.41 101.77 0 -0.24 0
951770042 3.69715 70 0.07 0.03 3.7 3.18 0.66 0.29 105.36 66 1.49 63 850140584 0.55 0.99 62.34 332.7 0.45 0.19 0.5 0 good 1.03 37.73 0.02 -0.11 0.17
951770049 19.4763 70 0.26 0.11 19.48 4.32 0.78 0.16 151.85 67 2.44 64 850140584 0.24 0.99 37.31 412.94 0.53 0.07 0.18 0.03 noise 0 103.9 0.02 -0.19 0.01
951770053 8.94733 110 0.23 0.01 8.95 3.36 0.31 0.16 138.79 68 2.11 65 850140584 0.19 0.97 23.11 275.88 0.49 0.1 0.18 0.02 good 0.65 35.97 0.04 -0.11 0.04
951770058 0.70961 70 -0.07 0.07 0.71 2.21 0.06 0.27 225.7 69 2.89 66 850140586 0.41 0.99 37.89 433.1 1 0.14 0.08 0 noise -0.14 16.76 0.11 -0.14 0.08
951770063 13.2811 110 -0.66 0.06 13.28 2.88 0.37 0.37 148.79 71 2.09 67 850140588 0.53 0.99 36.65 236.27 0.52 0.25 0.02 0.02 good 0.89 30.82 0.1 -0.13 0.05
951770068 38.2703 90 -0.88 0.04 38.27 3.77 0.88 0.36 119.2 72 1.94 68 850140588 0.57 0.99 36.2 173.36 0.46 0.22 0.02 0.05 good -0.55 117.2 0.02 -0.12 0.01
951770072 2.30067 70 -0.21 0.02 2.3 7.3 0.99 0.23 420.23 73 2.58 69 850140594 0.41 0.95 41.22 684.33 1.42 0.16 0 0 good 0 65.27 0 -0.26 1.23
951770077 0.30856 60 -0.41 0.11 0.31 5.68 1 0.26 448.59 74 3.28 70 850140594 0.35 0.56 13.18 82.33 1.94 0.15 0 0 good 0 56.98 0 -0.26 6.1
951770082 2.02931 170 0.13 0.05 2.03 2.95 0.12 0.63 89.09 75 0.94 71 850140590 0.21 0.99 56.57 429.87 0.33 0.19 0.46 0 good 0.1 21.5 0.12 -0 2.06
951770087 0.0124 150 -0.38 nan 0.01 4.5 nan 0.36 273.06 76 2.02 72 850140594 0.52 0.56 nan 0 1.07 0.26 0.36 0 noise 1.13 21.88 0.01 -0.17 0
951770091 1.88815 70 -0.14 0.08 1.89 3.93 0.74 0.18 264.93 77 2.03 73 850140594 0.77 0.98 37.32 223.1 1.12 0.12 0.04 0 good 0.34 36.82 0.02 -0.34 1.51
951770093 46.1365 50 -0.69 0.11 46.14 4.97 0.98 0.36 326.56 80 4.04 74 850140594 0.46 0.99 46.01 136.4 1.25 0.19 0.01 0 good 0.34 88.83 0 -0.24 0.02
951770098 0.03224 100 0.96 nan 0.03 2.9 0 0.37 354 82 2.62 75 850140594 0.47 0.77 0 0 1.28 0.23 0.29 0 good 0.69 13.58 0.08 -0.26 0
951770102 0.0094 170 -0.23 nan 0.01 2.49 nan 0.36 285 85 1.7 76 850140594 0.49 0.56 nan 0 1.1 0.25 0.5 0 noise -0.86 14.93 0.04 -0.12 0
951770105 0.01529 170 0.57 nan 0.02 2.8 nan 0.43 300.71 86 2.3 77 850140594 0.38 0.61 nan 0 1.1 0.25 0.08 0 good 0.62 14.39 0.03 -0.1 0
951770111 0.24811 80 -0.02 0.01 0.25 3.75 0.04 0.36 357.22 87 3.4 78 850140594 0.46 0.99 33.63 377.66 1.32 0.21 0.06 0 good 0 25.53 0.03 -0.24 0
951770116 0.01416 120 -0.04 nan 0.01 3.1 nan 0.34 293.05 88 2.3 79 850140594 0.46 0.5 nan 0 1.11 0.25 0.5 0 noise 0.1 16.69 0.01 -0.1 0
951770121 0.01157 130 -0.22 nan 0.01 3.13 nan 0.33 339.84 89 2.22 80 850140594 0.55 0.47 nan 0 1.33 0.27 0.5 0 noise 1.13 15.99 0.02 -0.25 0
951770127 0.02253 70 1.37 nan 0.02 3 nan 0.37 299.15 90 2.29 81 850140594 0.57 0.58 3.4 0 1.05 0.25 0.46 0 good -1.1 14.72 0.03 -0.19 0
951770132 2.404 70 0.34 0.04 2.4 4.39 0.91 0.43 284.85 91 1.86 82 850140588 1.09 0.95 32.72 117.11 0.53 0.16 0 0 good -0.14 34.48 0.02 -0.03 1.29
951770136 0.5267 60 0 -0.06 0.53 3.25 0.68 0.14 423.98 92 4.17 83 850140588 0.72 0.95 53.56 620.07 1.17 0.08 0.14 0 good -0.41 30.47 0.02 -0.72 0.42
951770142 2.90952 70 -0.41 -0.05 2.91 3.8 0.91 0.23 421.32 93 2.72 84 850140598 0.34 0.9 32.61 401.71 1.19 0.14 0.02 0 good 0 41.92 0.02 -0.19 1.04
951770147 2.11745 100 -0.27 0.07 2.12 4.08 0.51 0.29 135.46 94 2.24 85 850140600 0.41 0.99 15.38 287.17 0.61 0.18 0.5 0 good -0.67 34.01 0.02 -0.08 0.16
951770154 10.0171 110 0 0.05 10.02 4.48 0.94 0.26 113.24 95 2.01 86 850140600 0.42 0.99 29.48 170.62 0.5 0.16 0.5 0.02 good -0.59 61.71 0.01 -0.03 0.02
951770159 0.18766 90 -0.14 0.01 0.19 3.28 0.13 0.21 222.78 96 2.46 87 850140602 0.42 0.98 39.14 180.01 0.94 0.12 0.02 0 good 0.21 25.76 0.01 -0.24 3.3
951770164 5.28366 140 -2.94 0.04 5.28 4.22 0.92 0.12 184.76 97 2.02 88 850140602 0.37 0.99 27.41 407.05 0.44 0.07 0.5 0 noise 1.27 45.14 0.02 -0.29 1.11
951770170 17.817 60 0 0.11 17.82 6.54 1 0.33 268.16 98 3.39 89 850140602 0.65 0.99 34.5 101.59 1.13 0.16 0 0 good -0.07 86.21 0 -0.22 0
951770178 3.51083 170 0.18 -0.04 3.51 3.16 0.21 0.96 130.09 99 1.75 90 850140604 0.45 0.99 48.05 691.65 0.48 0.21 0.5 0 noise 0.3 21.79 0.17 -0.02 2.27
951770183 6.9079 40 0 0.1 6.91 3.64 0.92 0.23 142.64 100 0.76 91 850140610 0.4 0.99 38.61 332.62 0.24 0.11 0.1 0 good -0.69 50.71 0.01 -0.03 0.08
951770188 35.2797 100 -0.63 0.1 35.28 4.13 0.91 0.32 147.15 101 2.13 92 850140610 0.47 0.99 35.77 153.56 0.54 0.16 0 0.03 good -0.41 116.45 0.02 -0.05 0.01
951770196 8.93566 60 -0.76 0.05 8.94 3.23 0.57 0.27 186.73 102 2.62 93 850140610 0.33 0.99 12.03 236.13 0.84 0.14 0.08 0.02 good 0 42.86 0.05 -0.08 0.05
951770200 4.70416 100 -0.34 0.09 4.7 3.89 0.85 0.19 142.37 103 2.22 94 850140616 0.42 0.87 45.17 352.71 0.6 0.11 0.19 0.01 good 1.43 55.21 0.01 -0.16 0.16
951770205 6.16409 40 -0.34 0.08 6.16 3.53 0.94 0.16 96.12 104 1.64 95 850140616 0.23 0.99 18.27 222.84 0.36 0.11 0.07 0 good 0 59.14 0.01 -0.12 0.02
951770210 0.75301 90 -0.06 -0.09 0.75 2.4 0.43 0.19 115.4 105 1.71 96 850140616 0.17 0.92 56.28 287.9 0.47 0.12 0.24 0 good -0.21 29.08 0.02 -0.06 1.78
951770214 5.3033 110 0.15 0.07 5.3 4.74 0.95 0.32 183.12 106 2.48 97 850140618 0.49 0.99 34.34 229.12 0.78 0.18 0.5 0 good 0.55 58.16 0 -0.1 0.67
951770220 28.654 60 0.69 0.06 28.65 4.64 0.99 0.15 103.72 107 1.43 98 850140618 2.46 0.99 42.78 245.44 0.3 0.11 0.5 0.01 good 0.21 103.87 0 -0.08 0.01
951770224 8.07962 110 -0.14 0.04 8.08 3.29 0.87 0.19 126.87 108 1.89 99 850140620 0.65 0.97 42.43 224.3 0.56 0.16 0.1 0.01 good 0 50.51 0.02 -0.14 0.08
951770229 2.06527 80 -0.18 0.01 2.07 2.74 0.64 0.19 153.5 109 2.36 100 850140620 0.62 0.8 30.24 215.16 0.69 0.16 0.5 0 good 0 40.62 0.01 -0.21 0.42
951770234 22.1688 80 1.44 0.09 22.17 5.02 0.99 0.33 112.31 110 1.9 101 850140620 2.45 0.98 46.03 714.96 0.44 0.18 0.15 0 good 3.43 98.46 0 -0.06 0.19
951770238 5.75922 50 -0.62 0.08 5.76 6.37 0.94 0.18 224.87 111 3.07 102 850140626 0.75 0.74 38.07 120.45 0.9 0.1 0 0 good 0 88.3 0 -0.3 0.01
951770243 2.45495 150 1.06 -0.01 2.45 2.4 0.64 0.37 62.46 112 0.89 103 850140624 0.95 0.97 73.76 566.35 0.26 0.15 0.5 0 good 0.83 32.67 0.06 -0.03 1.03
951770248 0.73585 60 -0.89 -0.04 0.74 2.63 0.59 0.18 200.62 113 2.27 104 850140626 0.78 0.81 40.2 229.27 0.77 0.08 0.5 0 good 0.34 36.84 0.03 -0.23 23.6
951770251 2.08718 80 0.16 0.03 2.09 2.73 0.48 0.22 210.76 114 2.61 105 850140626 0.44 0.75 26.5 347.23 0.89 0.12 0.5 0 noise 0.34 25.71 0.08 -0.1 0.32
951770258 0.09435 50 -0.34 nan 0.09 3.28 0.07 0.16 229.4 115 2.54 106 850140626 0.76 0.6 14.69 59.72 0.82 0.1 0.5 0 noise 0 22.1 0.04 -0.3 43.51
951770264 0.13196 70 0.14 -0.01 0.13 3.64 0 0.16 274.62 116 3.29 107 850140626 0.62 0.65 21.45 1.39 0.97 0.1 0.46 0 good 0.34 27.36 0.01 -0.3 28.91
951770270 0.02542 50 0 nan 0.03 4.02 0 0.16 267.91 117 3.06 108 850140626 0.69 0.35 4.55 1.01 1.02 0.08 0.05 0 good 0.34 20.94 0.03 -0.32 119.87
951770276 3.03642 120 0.15 0.06 3.04 4.38 0.94 0.34 128.25 118 2.13 109 850140628 0.48 0.94 45.43 298.57 0.52 0.19 0.5 0 good 1.14 58.58 0 -0.08 0.31
951770283 13.0684 70 0.41 0.06 13.07 5.73 0.98 0.26 190.74 119 2.56 110 850140630 0.67 0.9 23.11 227.4 0.55 0.12 0 0 good 0.34 74.44 0 -0.05 0.13
951770288 36.0112 80 0.25 0.12 36.01 3.25 0.77 0.3 153.13 120 2.66 111 850140634 0.41 0.99 31.36 130.07 0.65 0.16 0.03 0.08 good 1.37 95.09 0.04 -0.09 0.02
951770295 7.37415 30 -0.69 0.13 7.37 6.91 0.99 0.19 306.54 121 3.84 112 850140634 0.71 0.99 30.58 200.82 1.27 0.14 0 0 good 0 77.07 0 -0.38 0.01
951770300 18.2104 110 0.13 0.02 18.21 2.17 0.39 0.34 153.27 122 2.41 113 850140634 0.43 0.99 44.85 276.04 0.62 0.21 0.05 0.05 good 0.96 36.88 0.13 -0.07 0.04
951770307 0.15242 130 0.86 nan 0.15 3.35 0 0.21 115.63 123 1.65 114 850140632 0.56 0.95 65.82 100.92 0.49 0.14 0.12 0 good -0.14 23.21 0.02 -0.12 5
951770312 3.81661 50 0 0.02 3.82 2.62 0.94 0.15 140.56 124 2.12 115 850140648 0.86 0.58 66.79 391.63 0.5 0.08 0.27 0 good 0.34 53.67 0.01 -0.25 0.25
951770315 12.5504 30 nan 0.1 12.55 3.14 0.95 0.21 157.43 125 2.39 116 850140642 0.58 0.99 25.87 187.11 0.65 0.11 0.46 0.01 good 1.03 67.15 0.01 -0.22 0.04
951770321 4.15937 80 0 0.05 4.16 2.7 0.56 0.26 193.61 126 2.85 117 850140642 0.4 0.98 11.46 252.35 0.85 0.15 0.5 0 good 0.62 33.43 0.04 -0.14 0.17
951770327 2.71463 40 0 0.07 2.71 2.73 0.85 0.41 146.48 127 2.13 118 850140644 0.43 0.96 20 145.37 0.64 0.15 0.01 0 good 1.37 52.57 0.01 -0.09 0.03
951770333 41.5639 60 0.55 0.07 41.56 6.24 1 0.21 165.13 128 2.36 119 850140652 0.57 0.99 34.12 168.9 0.7 0.12 0 0.01 good 0.69 131.45 0 -0.19 0
951770340 3.59846 60 -0.34 0.1 3.6 3.91 0.95 0.29 188.9 129 2.83 120 850140646 0.51 0.99 39.24 211.04 0.67 0.15 0.01 0 good -0.41 53.76 0.01 -0.1 0.01
951770347 2.79255 50 0.69 0.13 2.79 6.31 0.97 0.25 256.54 130 1.75 121 850140650 0.45 0.94 42.65 310.63 0.48 0.14 0.11 0 good -1.03 68.23 0 -0.07 0
951770353 0.00114 170 -0.06 nan 0 5.26 nan 0.23 210.46 131 2.78 122 850140648 1.11 0.03 nan 0 0.7 0.15 0.02 0 good 2.31 3.92584e+12 nan -0.2 0
951770358 15.6871 40 -0.69 0.12 15.69 5.28 1 0.25 143.9 132 2.5 123 850140644 0.63 0.99 20.33 153.75 0.56 0.11 0 0 good 0 109.94 0 -0.12 0.01
951770366 4.55928 50 -0.69 0.08 4.56 3.78 0.83 0.18 223.26 133 3.33 124 850140654 0.76 0.66 20.4 183.42 0.93 0.12 0.03 0 good -0.34 52.31 0.01 -0.28 0.13
951770375 0.00434 110 2.12 nan 0 4.2 nan 0.22 235.19 134 2.92 125 850140654 0.36 0.28 nan 0 0.96 0.11 0.5 0 good -2.27 136.3 0 -0.13 0
951770379 0.68574 50 -0.34 -0 0.69 3.62 0.51 0.59 151.05 136 1.77 126 850140654 2.03 0.54 38.24 204.81 0.35 0.18 0.01 0 good -1.03 37.46 0.01 -0.02 0.33
951770386 0.76241 70 -0.34 0.01 0.76 3.78 0.3 0.23 133.09 138 1.91 127 850140656 0.63 0.52 20.56 80.13 0.49 0.18 0.5 0 good 0 30.92 0.01 -0.1 0.6
951770391 0.38668 60 -0.34 0.02 0.39 3.83 0.5 0.19 248.05 139 3.53 128 850140658 0.73 0.68 16.37 86.8 1.04 0.11 0.01 0 noise -0.07 29.23 0.01 -0.37 0
951770397 0.05208 80 0 nan 0.05 1.75 0 0.16 135.36 140 2.04 129 850140648 0.73 0.51 22.79 19.63 0.51 0.1 0.5 0 good -0.16 21.58 0.01 -0.16 0
951770401 0.40373 60 -0.69 -0.01 0.4 3.83 0.23 0.19 223.85 141 3.36 130 850140658 0.77 0.67 22.13 73.22 0.96 0.12 0.01 0 noise -0.07 31.5 0.01 -0.34 0
951770406 3.30272 90 0.51 0.08 3.3 6.43 0.97 0.18 141.35 142 2.48 131 850140660 0.72 0.99 37.71 375.18 0.55 0.11 0.37 0 good 0 71.83 0 -0.18 0.03
951770412 4.56641 120 -0.02 0.07 4.57 4.93 0.94 0.33 118.2 143 2.07 132 850140662 0.42 0.67 19.81 140.13 0.48 0.19 0.5 0 good 0.89 74.99 0 -0.1 0.09
951770417 2.03014 60 -0.41 0.03 2.03 4.78 0.91 0.19 339.91 144 4.13 133 850140666 0.79 0.93 35.09 216.7 1.47 0.12 0 0 good 0.34 64.45 0 -0.56 0.15
951770423 40.8491 40 0 0.11 40.85 7.2 1 0.25 371.51 145 4.45 134 850140666 0.46 0.99 41.67 87.79 1.63 0.14 0 0 good 0 112.69 0 -0.34 0
951770428 7.49309 60 -0.34 0.04 7.49 4.21 0.99 0.21 155.43 146 2.14 135 850140666 0.51 0.99 32.61 203.61 0.68 0.12 0.3 0 good -0.21 79.27 0 -0.19 0.02
951770434 42.6069 50 0 0.16 42.61 4.18 0.98 0.18 369.72 147 5.05 136 850140668 0.48 0.99 41.06 86.15 1.54 0.11 0 0 good 0 74.52 0.01 -0.41 0
951770439 44.0604 110 0.07 0.07 44.06 4.34 0.98 0.32 132.86 148 2.05 137 850140668 0.58 0.99 44.66 197.53 0.54 0.21 0.08 0.02 good 1.2 103.78 0 -0.1 0.01
951770446 9.16289 110 -0.42 0.11 9.16 5 0.94 0.19 197.11 149 3.51 138 850140674 0.5 0.99 26.8 152.76 0.85 0.11 0 0 good 0.62 66.83 0.01 -0.23 0.01
951770452 3.19711 70 -0.41 0.05 3.2 3.93 0.85 0.26 144.35 150 2.91 139 850140674 0.65 0.99 22.87 281.43 0.63 0.14 0.5 0 good 0.27 59.35 0 -0.14 0.56
951770457 6.71766 100 -0.14 0.07 6.72 2.95 0.64 0.3 143.28 151 2 140 850140668 0.51 0.99 38.87 213.4 0.62 0.18 0.5 0 good 0.45 38.73 0.04 -0.11 0.19
951770465 8.21706 60 -1.03 0.09 8.22 4.38 0.87 0.26 109.62 152 2.39 141 850140676 0.64 0.99 22.67 217.42 0.51 0.15 0.5 0 good 0.62 56.1 0.01 -0.1 0.12
951770470 8.14875 70 -0.41 0.05 8.15 3.35 0.91 0.33 116.62 153 2.36 142 850140682 0.41 0.99 37.99 158.99 0.49 0.15 0.22 0.01 good 0.34 65.78 0.01 -0.09 0.04
951770477 37.1047 80 0 0.11 37.1 5.39 1 0.43 91.84 154 2.31 143 850140680 0.41 0.99 27 125.92 0.29 0.22 0 0 good 0.76 120.7 0 -0.06 0.01
951770484 5.17609 80 -0.33 0.08 5.18 3.76 0.92 0.18 160.58 155 3.33 144 850140682 0.7 0.99 33.45 173.54 0.66 0.1 0.01 0.01 good 0 63.06 0.01 -0.22 0.52
951770489 0.94955 80 -0.27 0.07 0.95 3.36 0.55 0.18 165.54 156 3.14 145 850140682 0.68 0.99 28.02 346.73 0.67 0.11 0.11 0 good 0.14 41.23 0.02 -0.23 1.8
951770497 0.73007 70 0.48 -0 0.73 3.55 0.76 0.3 115.64 157 2.59 146 850140682 0.47 0.98 17.91 285.93 0.5 0.18 0.5 0 good 0.69 46.19 0.01 -0.1 0.65
951770501 4.21404 80 -1.28 0.07 4.21 3.46 0.92 0.33 122.26 158 1.84 147 850140690 0.46 0.99 37.58 186.53 0.52 0.16 0.01 0 good 1.37 59.42 0.01 -0.09 0.03
951770508 1.8741 50 -0.34 0.03 1.87 3.62 0.71 0.29 140.8 159 1.97 148 850140690 0.48 0.99 10.54 274.94 0.61 0.16 0.5 0 good 1.03 42.46 0.02 -0.06 0.94
951770513 4.27707 70 -0.27 0.06 4.28 3.27 0.95 0.29 80.88 160 1.31 149 850140690 0.39 0.99 33.45 287.58 0.35 0.16 0.5 0.01 good -0.21 76.37 0 -0.04 0.13
951770519 0.70237 50 0 0.07 0.7 4.38 0.95 0.48 72.37 161 2.23 150 850140696 0.36 0.99 25.19 495.63 0.22 0.19 0.13 0 good -0.34 66.1 0 -0.03 0.16
951770525 1.99056 50 0.07 0.03 1.99 4.91 0.99 0.33 64.21 162 1.53 151 850140700 0.79 0.99 28.2 320.78 0.23 0.21 0.08 0 good 0.69 79.73 0 -0.03 0.31
951770530 0.0062 110 2.25 nan 0.01 2.66 0 0.19 91.84 163 2.03 152 850140696 0.33 0.32 nan 0 0.39 0.12 0.5 0 good 0.69 39.02 0 -0.07 0
951770536 0.05177 50 0.27 nan 0.05 3.9 0.06 0.23 96.13 164 2.48 153 850140702 0.75 0.49 22.02 39.59 0.28 0.12 0.12 0 good nan 34.73 0.01 -0.03 0
951770542 0.19747 40 -0.69 0.05 0.2 3.77 0.62 0.36 164.2 165 3.89 154 850140698 0.48 0.99 22.42 50.4 0.68 0.16 0.01 0 good 0 44.31 0 -0.14 0
951770548 1.45735 70 -0.82 0.08 1.46 3.87 0.94 0.21 110.11 166 2.73 155 850140698 0.34 0.98 15.96 358.93 0.47 0.11 0.02 0 good -0.34 63.03 0.01 -0.09 0.36
951770556 0.10809 10 nan nan 0.11 2.53 0.87 2.69 470.26 167 0.85 156 850140706 0.15 0.99 3.05 1.16 0.05 1.46 0.03 0 noise nan 41.68 0 -12.15 878.5
951770561 1.84444 50 0.55 0.07 1.84 5.79 1 0.33 104.45 168 0.41 157 850140706 0.54 0.96 14.49 235.11 0.44 nan 0.5 0 good -0.69 85.14 0 -0.11 1.18
951770569 0.14798 10 nan nan 0.15 2.95 0.91 0.03 477.46 169 1.12 158 850140706 0.06 0.99 29.27 36.84 12.48 1.69 0.03 0 noise nan 41 0.01 nan 1011.75
951770574 16.8392 10 nan 0.1 16.84 4.46 0.98 0.67 79.13 170 2.48 159 850140714 0.69 0.99 11.32 266.74 0.13 0.26 0.11 0.04 noise nan 142.44 0.01 -0.05 0.05
951770580 0.00765 100 0.17 nan 0.01 6.23 0 0.38 122.41 171 3.62 160 850140714 0.53 0.47 nan 0 0.47 0.19 0.37 0 noise 0.28 62.99 0 -0.09 0
951770586 7.93485 50 -2.75 0.05 7.93 3.84 0.88 0.63 54.73 172 1.64 161 850140714 0.36 0.99 24.63 211.48 0.16 0.18 0.27 0.01 good 0.21 58.83 0.06 -0.02 0.03
951770592 1.68127 90 0.41 0.08 1.68 3.48 0.79 0.41 62.78 173 2.2 162 850140722 0.38 0.99 19.65 491.02 0.22 0.19 0.5 0.01 good 0.55 47.13 0.03 -0.02 2.9
951770599 0.13227 90 -0.48 -0.04 0.13 3.24 0.18 0.4 62.92 174 2.05 163 850140722 0.58 0.99 21.3 33.44 0.25 0.16 0.17 0 good 0.69 31.26 0.03 -0.06 13.28
951770604 5.58602 60 0.34 0.05 5.59 4.4 0.96 0.56 53.15 175 2.13 164 850140726 0.38 0.99 15.71 286.71 0.19 0.19 0.1 0.02 good 0.41 77.9 0.01 -0.02 0.05
951770610 0.3222 60 -0.48 0.12 0.32 7.94 0.99 0.3 173.69 176 4.19 165 850140730 0.63 0.99 27.61 135.6 0.79 0.21 0 0 good 0.34 76.53 0 -0.14 0
951770618 0.14901 60 0.89 nan 0.15 4.03 0.61 0.23 58.39 177 1.99 166 850140732 1.4 0.7 40.83 196.78 0.26 0.22 0.22 0 good -0.34 44.42 0 -0.08 1.74
951770623 0.16317 60 0.34 0.06 0.16 4.93 0.5 0.52 86.42 178 3.04 167 850140732 0.99 0.85 46.81 399.88 0.15 0.23 0.05 0 noise -0.34 52.97 0 -0.01 0
951770630 0.05311 60 0.34 nan 0.05 8.35 0.99 0.15 92.07 179 3.29 168 850140732 1 0.47 28.61 160.85 0.34 0.16 0.12 0 noise 0 88.32 0 -0.14 0
951770636 1.18382 10 nan 0.04 1.18 nan 1 1.84 54.58 180 2.53 169 850140766 0.05 0.99 8.77 327.12 0.22 0.16 0.5 nan noise nan nan nan -0 1.38
951770641 1.42738 90 nan -0.16 1.43 nan nan 1.74 51.54 181 0.5 170 850140810 0.48 0.99 45.53 1604.8 -0 0.78 0.5 0 noise 7.53 nan nan -0.01 3.48
951770647 2.63909 170 2.69 0 2.64 1.76 0.1 2.03 29.66 182 0.69 171 850140818 1.27 0.99 28.91 967.29 0.01 1.33 0.5 0.02 noise 0 22 0.27 -0.54 0.8
951770653 0.93426 100 3.43 -0.01 0.93 nan nan 1.47 40.5 183 0.78 172 850140814 0.47 0.99 48.87 1634.65 0.01 0.99 0.5 0 noise 6.73 nan nan -0.03 20.63
951770658 3.0141 100 5.49 0.01 3.01 nan nan 2.07 32.36 184 0.91 173 850140814 0.21 0.99 32.84 1133.7 0.01 1.44 0.5 0 noise 5.93 nan nan -0.45 0.71
951770663 21.2313 170 1.47 0.04 21.23 1.82 0.87 1.51 17.94 185 0.5 174 850140826 0.11 0.99 17.75 305.11 0.04 1.18 0.27 0.26 noise -0.69 7420.02 0.06 -0.08 0.02
951770670 1.88836 170 0.97 -0.03 1.89 nan nan 0.76 28.33 186 0.23 175 850140834 1.24 0.99 55.9 1266.76 0.02 1.47 0.5 0 noise -0.49 nan nan nan 1.68
951770674 2.97886 120 0.21 -0.01 2.98 3.41 0.69 0.22 53.25 187 0.99 176 850140824 0.28 0.99 20.27 518.34 0.23 0.15 0.5 0.01 noise 0.23 34.62 0.16 -0.03 3.43
951770680 0.01767 130 1.59 nan 0.02 4.33 0 0.63 92.31 188 0.27 177 850140838 2.26 0.53 0 0 0.05 1.61 0.46 0 good -2.99 36.58 0.01 nan 124.04
951770685 0.08742 120 -0.07 nan 0.09 nan nan 0.41 68.27 189 0.99 178 850140824 0.18 0.83 32.63 127.57 0.27 0.15 0.1 0 noise -0.76 nan nan -0.01 45.61
951770691 0.94656 80 0.55 0.01 0.95 3.13 0.43 0.15 83.02 190 1.46 179 850140826 0.76 0.99 25.88 886.03 0.28 0.08 0.5 0.01 good 10.78 29.14 0.17 -0.15 5.53
951770696 0.0744 70 -0.34 nan 0.07 4.51 0.17 0.78 96.88 191 1.49 180 850140826 0.2 0.99 16.43 9.28 0.38 0.15 0.16 0 good 0.21 37.62 0 -0.02 7
951770704 0.95203 80 0.62 0 0.95 3.23 0.37 0.15 84.93 192 1.45 181 850140826 0.73 0.99 41.81 875.97 0.26 0.1 0.32 0.01 noise -3.5 28.23 0.19 -0.15 8.08
951770708 1.23135 90 -1.24 0.07 1.23 4.8 0.85 0.37 89.25 193 1.28 182 850140828 0.22 0.99 14.91 445.49 0.37 0.15 0.08 0 good 0.41 46.29 0.02 -0.03 2.02
951770714 1.40785 110 -1.51 0.04 1.41 5.04 0.85 0.34 95.96 194 1.36 183 850140828 0.34 0.99 16.44 344.56 0.38 0.18 0.02 0 good 7.33 44.4 0.03 -0.04 0.33
951770720 12.3374 60 -0.34 0.3 12.34 25.57 1 0.23 943.27 195 8.54 184 850140832 0.58 0.99 29.27 155.51 4.25 0.16 0 0 good 0.41 508.97 0 -1.05 0.07
951770728 13.9405 80 -0.21 0.32 13.94 12.36 1 0.25 362.01 196 5.11 185 850140842 0.5 0.99 27.25 56.38 1.65 0.12 0 0 good 0.14 365.02 0 -0.36 0
951770735 1.29015 170 -4.46 -0.04 1.29 1.26 0.04 1.9 36.06 197 0.33 186 850140842 0.11 0.99 43.02 1688.73 0.01 1.57 0.37 0.01 noise 4.52 17.81 0.41 -0.22 1.16
951770742 3.76835 80 -0.07 0.2 3.77 4.43 0.99 0.23 190.47 198 2.47 187 850140850 0.6 0.99 19.09 119.39 0.83 0.12 0 0 good -0.41 62.15 0.01 -0.19 0.03
951770748 1.0222 70 -0.34 0.19 1.02 4.39 0.78 0.49 135.47 199 1.67 188 850140850 0.48 0.99 25.05 184.35 0.49 0.19 0 0 good 0.34 44.42 0.02 -0.08 0.48
951770755 7.26544 70 -0.34 0.26 7.27 10.95 1 0.18 202.17 200 3.33 189 850140852 0.65 0.99 31.33 116.81 0.8 0.1 0 0 good -0.21 140.96 0 -0.25 0.07
951770760 0.29544 160 -3.81 -0.02 0.3 2.75 0.08 1.81 92.28 201 0.35 190 850140838 0.57 0.98 59.04 1308.51 0.02 1.3 0.09 0 noise 1.95 20.03 0.22 -1.08 0.44
951770768 0.5141 140 -1.04 -0.08 0.51 nan nan 2.09 130.65 202 0.6 191 850140838 2.22 0.99 66.26 1705.11 0.09 1.22 0.07 0 noise -6.17 nan nan -2.07 0.59
951770773 11.2351 140 -0.15 0.1 11.24 3.42 0.94 0.36 60.57 203 1.46 192 850140862 0.23 0.99 8.99 205.99 0.24 0.16 0.07 0.05 noise -0.12 83.25 0.03 -0.03 0.1
951770780 3.64 150 1.2 0.04 3.64 2.2 0.43 0.25 44.08 204 0.92 193 850140862 0.28 0.99 30.03 508.67 0.2 0.18 0.42 0.04 good 0.34 35.24 0.19 -0.03 1.19
951770785 3.57532 150 -1.99 0.01 3.58 2.67 0.59 0.26 57.22 205 1.2 194 850140862 0.33 0.99 12.01 272.47 0.26 0.16 0.5 0.06 noise 0.34 40.84 0.12 -0.05 1.67
951770791 0.00537 170 4.04 nan 0.01 6.33 0 1.77 123.8 206 0.65 195 850140858 11.88 0.36 nan 0 0.2 0.32 0.5 0 noise 1.82 82.28 0 -0.05 0
951770795 1.7439 160 -0.57 0.01 1.74 1.88 0.25 1.24 32.74 207 0.38 196 850140862 0.53 0.99 37.45 983.23 0.02 0.91 0.5 0.03 noise 0.54 28.4 0.35 -0.02 2.78
951770802 0.4058 110 -5.97 -0 0.41 2.03 0.12 2.02 113.62 208 1.4 197 850140882 0.73 0.99 51.08 1454.47 0.03 1.44 0.23 0 noise 4.81 18.18 0.61 -2.44 0.24
951770808 0.29275 170 3.45 -0.08 0.29 nan nan 1.95 86.31 209 0.87 198 850140882 1.09 0.99 76.73 1686.81 0.01 1.52 0.05 0 noise -6.49 nan nan -1.48 0
951770814 2.82355 110 -1.82 0.03 2.82 1.33 0.22 1.65 44.17 210 0.43 199 850140862 0.15 0.99 21.47 657.62 0.02 1.61 0.46 0.08 noise -0.8 31.01 0.36 -0.32 0.23
951770822 5.15015 160 2.87 -0.01 5.15 1.81 0.53 1.8 27.94 211 0.56 200 850140878 6.18 0.99 21.33 707.54 0.01 2.02 0.23 0.14 noise -8 44.81 0.24 -0.29 0.05
951770828 2.51685 170 4.96 -0.02 2.52 4.04 0.93 2.09 33.74 212 0.6 201 850140882 2.3 0.99 31 1116.62 0.01 1.37 0.5 0.02 noise -0.02 59.97 0.01 -0.61 0.33
951770834 9.90298 170 -7.12 0.01 9.9 1.44 0.76 0.03 27.76 213 0.68 202 850140882 1.22 0.99 11.84 323.19 0.46 0.84 0.11 0.34 noise 1.03 110 0.19 nan 0.07
951770842 3.29125 140 -6.23 0.04 3.29 4.23 0.99 0.15 57.52 215 1.7 203 850140904 1.36 0.99 34.69 663.04 0.21 0.14 0 0 noise -2.4 52.29 0.06 -0.08 0.02
951770847 0.00434 170 -5.3 nan 0 5.98 0 0.14 67.28 216 1.61 204 850140904 1.02 0.28 nan 0 0.19 0.14 0.5 0 good -0.37 209.45 0 -0.12 0
951770854 1.60326 170 0.27 0.06 1.6 3.44 0.91 1.02 30.97 217 0.54 205 850140930 2.05 0.99 33.78 870.71 0.02 1.63 0.45 0.01 noise 3.41 63.47 0.03 nan 28.7
951770860 2.06372 80 0 0.01 2.06 3.29 0.89 0.41 57.98 218 1.35 206 850140922 0.54 0.99 29.27 327.82 0.2 0.19 0.42 0.04 good 0.34 55.87 0.06 -0.03 3.13
951770867 2.47717 30 0 0.1 2.48 4.99 0.99 0.29 107.69 219 3.07 207 850140926 0.32 0.99 14.94 260.65 0.4 0.1 0.06 0 noise 0 73.23 0 -0.08 0.16
951770873 3.86228 140 0.06 0.06 3.86 2.22 0.61 0.49 45.86 220 1.1 208 850140930 0.6 0.99 50.01 374.91 0.14 0.25 0.5 0.1 good 3.75 43.83 0.2 -0.04 3.25
951770880 0.34214 170 -1.22 nan 0.34 2.1 0.19 2.29 73.36 221 0.94 209 850140938 0.42 0.99 40.32 523.78 0.01 1.26 0.17 0 noise 7.06 21.31 0.45 -0.92 77.8
951770886 1.24447 20 0 0.13 1.24 5.34 0.98 0.3 122.43 222 3.39 210 850140938 0.15 0.99 14.56 185.76 0.47 0.1 0.03 0 noise nan 59.15 0.01 -0.05 0.03
951770891 3.36224 170 0.8 0.05 3.36 1.44 0.55 2.09 32.97 223 0.78 211 850140938 0.21 0.99 49.71 544.7 0.05 0.87 0.5 0.11 noise -0.15 41.35 0.19 -0.37 3.3
951770896 4.17508 160 -0.23 0.03 4.18 1.9 0.68 0.41 42.46 224 1.13 212 850140940 0.42 0.99 46.49 337.13 0.13 0.27 0.5 0.21 noise 3.61 50.87 0.17 -0.02 1.56
951770901 2.79089 150 -0.59 0.08 2.79 3.89 0.9 0.36 47.42 225 1.52 213 850140952 0.15 0.99 35.28 357.44 0.2 0.21 0.5 0.03 noise -0.33 60.98 0.04 -0.02 0.87
951770908 0.65711 40 -1.37 0.16 0.66 7.72 1 0.67 170.28 226 3.49 214 850140954 0.28 0.94 41.4 57.42 0.6 0.16 0 0 good -0.34 131.59 0 -0.05 0
951770914 2.69304 170 -2.72 0.02 2.69 2.64 0.75 1.11 33.99 227 0.64 215 850140954 0.42 0.99 33.85 871.98 0.01 1.06 0.5 0.02 noise -1.83 49.23 0.05 -0.03 5.7
951770921 2.56759 170 0.1 -0.01 2.57 nan nan 0.89 31.68 228 0.71 216 850140958 0.34 0.99 47.97 1370.9 0.04 1.33 0.5 0 noise 2.85 nan nan nan 6.84
951770928 3.41143 160 -2.11 0.11 3.41 4.31 0.95 0.73 47.58 229 1.34 217 850140962 0.06 0.99 31.51 377.62 0.09 0.47 0.4 0.01 good -1.52 74.08 0.03 -0.01 0.75
951770943 0.82007 150 -2.38 0.06 0.82 2.38 0.88 0.66 109.81 231 2.32 218 850140968 0.2 0.97 32.85 269 0.29 0.29 0.34 0 noise -0.29 36.12 0.04 -0.02 1.96
951770949 7.27515 120 -4.33 0.19 7.28 5.55 0.99 0.8 99.99 232 2.61 219 850140968 0.2 0.98 24.7 252.31 0.21 0.34 0 0 good -0.43 110.53 0 -0.02 0.01
951770955 3.869 130 -2.95 0.07 3.87 3.16 0.87 0.92 75.45 233 1.42 220 850140970 0.27 0.99 38.73 175.86 0.09 0.38 0 0 good -0.24 49.04 0.02 -0.01 0.48
951770960 3.89628 100 -3.43 0.25 3.9 7.32 1 0.92 121.58 234 3.03 221 850140976 0.16 0.71 7.5 73.34 0.35 0.25 0 0 good -0.04 135.09 0 -0.03 0
951770965 2.26109 140 -2.29 0.13 2.26 5.09 0.99 0.98 116.46 235 2.31 222 850140984 0.26 0.99 52.89 400.94 0.34 0.18 0 0 good -0.57 65.91 0 -0.02 0.05
951770969 0.96547 120 -0.64 0.22 0.97 4.8 0.98 0.71 162.48 236 2.3 223 850140994 0.34 0.98 40.41 273.39 0.4 0.22 0 0 noise 0.82 55.24 0 -0.01 0.04
951770976 5.17216 140 -2.16 0.13 5.17 2.55 0.75 0.98 60.8 237 1.12 224 850140986 0.16 0.99 36.81 324.83 0.14 0.33 0.21 0.01 good 0.65 45.1 0.04 -0.02 0.61
951770981 3.4756 120 -3.51 0.07 3.48 2.9 0.75 0.77 62.32 238 1.47 225 850140978 0.32 0.99 36.57 275.61 0.15 0.27 0.5 0.01 good 0.02 48.33 0.02 -0.01 0.66
951770987 3.96231 170 -2.09 0.05 3.96 2.48 0.95 0.78 40.64 239 0.72 226 850140972 0.41 0.97 91.04 750.16 0.06 0.4 0.13 0.01 good -0.64 72.64 0.01 -0.01 0.91
951770994 7.32072 110 -2.47 0.06 7.32 3.4 0.99 0.67 52.32 240 1.27 227 850140980 0.28 0.99 35.34 230.74 0.13 0.3 0.16 0 good 0.39 86.45 0 -0.01 0.39
951771000 1.40661 120 -2.69 0.09 1.41 3.05 0.92 0.78 130.76 241 2.15 228 850140976 0.17 0.8 57.42 454.14 0.22 0.3 0.07 0 noise -0.56 49.46 0.01 -0.01 0.39
951771005 4.06492 110 -1.77 0.16 4.06 3.26 0.66 0.69 118.61 242 2.17 229 850140986 0.13 0.99 42.22 252.8 0.39 0.22 0 0.01 good 0.27 31.38 0.07 -0.01 0.42
951771013 5.3747 100 -2.38 0.06 5.37 1.92 0.66 0.8 91.89 243 1.94 230 850140986 0.15 0.99 31.97 182.88 0.26 0.26 0.04 0.01 good -0.14 39.4 0.04 -0.02 0.47
951771018 1.93496 60 -1.99 0.08 1.93 4.08 0.83 0.95 149.97 244 3.01 231 850140986 0.15 0.92 17.95 74.89 0.5 0.18 0 0 good -0.34 44.48 0.01 -0.03 0.32
951771024 8.65086 120 -2.5 0.04 8.65 2.72 0.85 0.69 105.93 245 2.25 232 850140986 0.11 0.99 55.11 239.67 0.32 0.23 0 0.01 good 0.22 48.38 0.03 -0 0.13
951771032 6.05693 120 -1.67 0.04 6.06 1.74 0.59 0.82 58.93 246 0.89 233 850140994 0.4 0.99 78.75 371.29 0.16 0.22 0.5 0.02 good 0.62 37.98 0.05 -0.01 0.37
951771038 1.6262 130 -1.28 0.03 1.63 2.04 0.43 0.88 75.35 247 0.78 234 850140994 0.8 0.99 40.18 407.6 0.14 0.29 0.5 0 noise -0.89 29.33 0.06 -0.02 1.99
951771043 1.92535 80 -1.08 0.16 1.93 3.73 0.8 0.95 264.48 248 3.13 235 850140994 0.25 0.99 39.3 199.48 0.85 0.16 0 0 good -0.69 41.36 0.01 -0.04 0.21
951771050 10.1953 80 0.27 0.08 10.2 3.51 0.99 0.32 78.07 249 1.7 236 850140990 0.44 0.99 58.09 205.4 0.34 0.19 0.04 0 good 0.14 75.2 0 -0.08 0.02
951771057 5.83796 140 -2.43 0.06 5.84 2.33 0.79 1.11 69.59 250 1.36 237 850140990 0.27 0.99 69.39 285.31 0.16 0.27 0.5 0.01 good -0.9 46.61 0.02 -0.02 0.54
951771064 14.5114 100 -2.47 0.06 14.51 3.43 0.99 0.88 72.08 251 0.84 238 850140994 0.38 0.99 39.99 141.15 0.14 0.18 0.01 0 good 0 74.75 0 -0.01 0.26
951771069 2.92957 80 -0.89 0.17 2.93 4.73 0.97 1 163.51 252 2.44 239 850140992 0.3 0.99 65.95 195.28 0.51 0.22 0 0 good 0.48 68.9 0 -0.03 0.27
951771077 0.01912 120 -1.21 nan 0.02 4.03 0 0.12 178.79 253 1.03 240 850140992 1.07 0.62 nan 0 0.31 0.07 0.27 0 good 1.72 34.59 0 -0.26 0
951771083 3.73104 90 -2.85 0.16 3.73 2.9 0.92 0.81 164.62 254 2.22 241 850140994 0.32 0.86 31.56 86.26 0.4 0.27 0 0 good -0.69 48.72 0.01 -0.03 0.01
951771089 1.26979 80 -1.31 0.11 1.27 4.83 0.71 1.06 269.33 255 3.18 242 850140994 0.2 0.87 5.26 107.68 0.99 0.14 0 0 good -0.34 41.26 0.01 -0.04 0.79
951771095 3.76111 100 -3.37 0.05 3.76 2.64 0.83 1.15 74.17 256 1.1 243 850140994 0.3 0.99 43.44 278.68 0.15 0.3 0.41 0 noise 1.37 48.85 0.01 -0 0.19
951771103 4.8884 120 -2.1 0.06 4.89 2.49 0.64 0.91 77.75 257 1.18 244 850140994 0.57 0.99 69.41 293.62 0.16 0.26 0.1 0.01 good 1.72 37.33 0.04 -0.03 0.19
951771110 5.96702 100 -1.47 0.06 5.97 1.77 0.79 0.99 90.26 258 1.31 245 850140994 0.35 0.99 56.2 210 0.27 0.22 0.22 0.01 good -0.34 40.74 0.04 -0.01 0.39
951771115 0.84911 120 -1.75 0.03 0.85 2.73 0.61 1.04 113.59 259 1.3 246 850140994 0.35 0.9 29.36 347.21 0.31 0.11 0 0 good 0.27 31.89 0.02 -0.02 0.05
951771121 3.54969 90 -0.81 0.13 3.55 3.98 0.98 0.92 201.95 260 1.94 247 850140996 0.25 0.99 56.4 139.67 0.46 0.16 0 0 good 0.69 52.22 0.01 -0.03 0.15
951771128 6.16161 100 -0.74 0.12 6.16 2.79 0.76 0.98 87.83 261 1.38 248 850140996 0.43 0.99 50.3 217.02 0.2 0.26 0.03 0.01 good -1.1 56.07 0.01 -0.01 0.28
951771135 3.06256 60 -1.44 0.13 3.06 3.26 0.98 0.87 150.95 262 1.63 249 850140996 0.39 0.97 42.7 128.39 0.25 0.19 0 0 good 0.69 63.82 0 -0.04 0.1
951771142 4.31344 90 -1.2 0.23 4.31 4.41 0.93 1.09 249.39 263 3.57 250 850140996 0.22 0.99 56.91 255.45 0.88 0.18 0 0 good -0.34 54.58 0 -0.02 0.11
951771148 2.52987 110 -1.87 0.06 2.53 2.36 0.95 1.09 131.66 264 1.81 251 850140996 0.27 0.99 71 164.37 0.45 0.16 0 0 good -0.34 44.69 0.01 -0.02 0.16
951771155 0.56235 100 -1.42 -0.12 0.56 3.26 0.69 0.55 126.18 266 1.43 252 850140996 0.31 0.88 27.74 131.63 0.36 0.18 0.02 0 good 0 36.77 0.01 -0.02 0.24
951771161 8.70253 110 -1.03 0.09 8.7 2.62 0.84 0.82 84.74 267 1.47 253 850140996 0.47 0.99 56.51 245.65 0.21 0.22 0.29 0.01 good -0 65.02 0.01 -0.02 0.31
951771167 7.51086 120 -0.17 -0.04 7.51 2.64 0.52 0.23 72.71 268 0.98 254 850140996 0.6 0.99 70.82 323.44 0.3 0.1 0.5 0.01 good -0.82 44.15 0.03 -0.04 0.42
951771174 9.14336 90 -0.26 0.01 9.14 3.1 0.71 0.23 94.07 269 1.49 255 850140996 0.38 0.99 65.03 232.98 0.41 0.11 0.13 0.02 good 0 54.71 0.02 -0.06 0.07
951771180 7.4625 100 -0.69 0.06 7.46 3.68 0.97 0.27 115.05 270 1.65 256 850140996 0.58 0.99 64.14 133.51 0.49 0.12 0.02 0 good 0.86 58.69 0 -0.08 0.09
951771188 3.9774 110 -1.1 -0.01 3.98 1.89 0.51 0.89 73.06 271 1.1 257 850140996 0.59 0.99 81.61 412.79 0.13 0.29 0.41 0.01 good -0.41 35.74 0.04 -0.02 0.69
951771194 0.02645 70 -1.65 nan 0.03 4.38 0 0.91 142.3 272 1.31 258 850140996 0.37 0.76 0 0 0.42 0.25 0 0 noise 0.69 32.8 0 -0.01 0
951771199 7.97298 70 -1.65 0.02 7.97 3.78 0.99 1.03 183.68 273 2.79 259 850140998 0.2 0.99 56.73 80.21 0.67 0.23 0 0 good 0.34 73.61 0 -0.02 0.02
951771206 2.36866 70 -0.96 0.04 2.37 3.3 0.71 0.84 192.27 274 2.25 260 850140994 0.36 0.99 56.69 155.85 0.63 0.25 0 0 good 0.21 41.54 0.01 -0.04 0.65
951771211 5.55864 80 -1.1 0.09 5.56 4.29 0.92 0.8 198.1 275 3.23 261 850140998 0.24 0.99 48.48 78.67 0.65 0.16 0 0 good 0 57.58 0 -0.04 0.05
951771218 0.38296 110 -2.03 -0.1 0.38 3.3 0.69 1.04 102.21 276 1.12 262 850140998 0.36 0.98 24.99 372.94 0.26 0.33 0.13 0 good 1.37 35.13 0.01 -0.01 2.9
951771224 7.28487 90 -1.28 0.03 7.28 2.84 0.91 0.99 81.86 277 1.22 263 850140998 0.3 0.99 50.1 131.94 0.21 0.23 0.16 0.01 good 2.4 50.66 0.01 -0.01 0.14
951771229 2.20705 90 -1.1 0.07 2.21 3.21 0.72 0.87 141.76 278 1.97 264 850140998 0.34 0.99 47.35 141.64 0.35 0.25 0.01 0 good 1.85 34.87 0.03 -0.02 0.62
951771234 1.37302 110 -1.16 0.01 1.37 2.22 0.57 1.1 80.68 279 1.25 265 850141000 0.29 0.99 50.35 416.18 0.25 0.23 0.1 0 good 0.34 29.81 0.05 -0.02 0.78
951771239 2.48233 90 -1.04 0.15 2.48 4.63 0.93 0.89 169.28 280 2.69 266 850141000 0.3 0.98 34.16 99.16 0.49 0.19 0 0 good -0.41 55.17 0 -0.04 0.18
951771246 1.51552 100 -0.88 0.04 1.52 2.15 0.61 1 95.35 281 1.55 267 850141000 0.26 0.99 63.3 334.45 0.28 0.21 0.14 0 good -0.55 32.15 0.04 -0.02 1.57
951771252 0.91514 140 -1.05 -0.06 0.92 2.39 0.1 1.55 78.04 282 0.62 268 850140998 0.93 0.99 47.95 1220.68 0.03 0.89 0.5 0 noise -0.2 20.6 0.16 -0.06 12.3
951771257 0.14436 140 0.38 nan 0.14 2.86 0.38 0.84 236.74 283 1.12 269 850141002 1.61 0.95 21.67 92.35 0.12 1.5 0.05 0 noise 0.51 12.46 0.45 nan 308.52
951771263 5.93799 120 -2.12 0.04 5.94 2.29 0.71 1.02 71.65 284 1.01 270 850140994 0.43 0.99 60.9 260.65 0.14 0.26 0.26 0.01 good 0.96 41.1 0.03 -0.02 0.48
951771270 0.87722 60 -1.1 -0.05 0.88 2.51 0.51 0.76 236.39 285 1.87 271 850141002 0.36 0.98 59.01 860.16 0.87 0.16 0.5 0 noise 0.34 20.06 0.08 -0.05 8.81
951771276 0.47348 150 -0.16 nan 0.47 1.64 0.01 1.83 85.51 286 0.59 272 850140998 0.03 0.99 53.34 823.14 0.02 1.98 0.27 0 noise 3.09 15.54 0.15 -0.7 19.18
951771283 3.91767 90 -0.84 0.08 3.92 3.48 0.86 0.78 138.84 287 2.12 273 850141002 0.29 0.99 51.83 230.58 0.43 0.18 0.01 0 good 0.62 47.79 0.01 -0.04 0.91
951771288 23.3667 70 0 0.12 23.37 3.57 0.97 0.29 172.63 288 3.41 274 850141004 0.51 0.99 68.31 83.37 0.73 0.14 0 0.01 good 0.82 64.31 0.01 -0.13 0.01
951771294 1.09433 90 -0.69 -0 1.09 3.21 0.68 0.82 106.44 289 1.78 275 850141004 0.39 0.99 40.82 281.53 0.31 0.22 0.01 0 good 1.3 39.71 0.01 -0.03 0.39
951771300 1.47967 150 0.22 0.03 1.48 2.46 0.32 0.88 52.48 291 0.38 276 850140998 1.69 0.99 47.28 1029.86 0.05 1.52 0.48 0 noise 0.11 30.32 0.07 nan 8.05
951771307 1.63054 170 6.49 0.02 1.63 2.15 0.38 1.65 51.63 292 0.39 277 850141002 36.9 0.99 33.91 720.14 0.04 1.14 0.5 0 noise -2.77 27.63 0.12 -0.3 24.45
951771313 24.9118 70 0 0.09 24.91 5.24 1 0.29 85.85 293 2.4 278 850141012 0.37 0.99 46.83 76.39 0.37 0.18 0 0 good -0.14 122.14 0 -0.07 0
951771320 6.55645 80 0.14 0.14 6.56 3.92 0.85 0.38 113.32 294 3.06 279 850141018 0.42 0.99 45.05 114.55 0.44 0.16 0 0.01 good 0.27 58.26 0.02 -0.06 0.07
951771326 3.15164 60 0.34 0.06 3.15 3.44 0.94 0.58 49.68 295 1.46 280 850141018 0.55 0.99 45.58 197.9 0.15 0.25 0.26 0 good 0.48 58.92 0.01 -0.02 0.21
951771331 7.01433 110 -0.12 0.08 7.01 3.41 0.92 0.38 75.72 296 2.12 281 850141018 0.48 0.99 44.2 136.49 0.3 0.18 0.03 0.02 good 0.1 70.11 0.01 -0.05 0.13
951771338 2.82262 140 -6.04 0.07 2.82 3.58 0.94 0.41 54.33 297 1.3 282 850141020 0.69 0.99 41.16 307.6 0.2 0.18 0.5 0 good -0.06 56.72 0.01 -0.01 1.1
951771344 1.48122 30 -1.37 0.05 1.48 4.22 0.99 0.33 69.02 298 2.1 283 850141024 0.16 0.69 21.2 156.75 0.28 0.12 0.04 0 noise 0.69 80.13 0 -0.04 0.04
951771349 0.00496 160 -1.19 nan 0 6.56 nan 0.34 99.13 301 2.93 284 850141024 0.18 0.15 nan 0 0.37 0.12 0.5 0 good 0.43 68.49 0 -0.03 0
951771357 0.39929 40 15.8 0.01 0.4 4.59 0.92 0.8 44.87 302 1.27 285 850141026 1.94 0.63 35.68 377.42 -0.04 0.21 0.31 0 good -7.9 57.66 0 -0.01 0.49
951771362 2.05752 20 nan 0.05 2.06 6.98 1 0.34 100.46 303 2.94 286 850141026 0.17 0.75 6.27 53.23 0.38 0.1 0.15 0 noise 0 102.24 0 -0.03 0.83
951771368 5.53353 20 0.69 0.11 5.53 3.87 0.82 0.49 83.09 304 2.44 287 850141036 4.93 0.98 35.48 781.5 0.26 0.11 0.5 0.01 good nan 84.3 0.02 -0.01 0.09
951771374 7.31979 30 -0.69 0.06 7.32 5.15 1 0.3 101.68 305 2.66 288 850141036 0.21 0.98 20.38 120.65 0.42 0.1 0.19 0 good 0 97.88 0 -0.06 0.3
951771381 2.6857 30 -2.06 0.01 2.69 3.43 0.62 0.38 94.3 306 0.65 289 850141040 15.33 0.87 51.99 346.8 0.08 0.19 0.26 0.02 noise nan 51.46 0.02 -0 0.81
951771387 16.6017 50 0 0.07 16.6 4.36 1 0.18 101.43 307 3.03 290 850141042 2.06 0.99 24.97 450.92 0.42 0.12 0.05 0 good 0.34 120.38 0 -0.24 0.01
951771393 1.57887 70 0 0.07 1.58 4.26 0.98 0.89 67.36 308 1.76 291 850141042 0.7 0.99 50.87 523.67 0.16 0.22 0.5 0 good 0.69 74.2 0 -0.02 0.12
951771400 1.9175 50 1.1 0.05 1.92 3.14 0.75 0.52 59 309 1.47 292 850141044 11.05 0.98 42.41 1271.77 0.18 0.15 0.5 0.01 good 0.69 43.73 0.02 -0.02 0.17
951771405 5.89996 30 -0.69 0.11 5.9 4.49 1 0.3 121.72 310 3.12 293 850141044 0.3 0.9 11 137.29 0.51 0.08 0.37 0 good 0 94.54 0 -0.08 0.4
951771412 1.98229 70 -0.21 0.08 1.98 2.58 0.74 0.78 74.85 311 1.91 294 850141044 0.45 0.99 56.69 428.97 0.2 0.21 0.47 0 good 0.21 48.59 0.01 -0.01 0.82
951771418 3.86786 70 -0.41 0.07 3.87 3.11 0.95 0.87 66.97 312 1.94 295 850141044 0.59 0.99 59.15 247.96 0.16 0.23 0.02 0.01 good 0.62 71.55 0 -0.01 0.08
951771425 0.40549 70 0 0.17 0.41 4.3 0.81 0.88 104.1 313 2.48 296 850141044 0.42 0.98 46.87 114.72 0.27 0.18 0 0 good -0.21 53.82 0 -0.02 0
951771431 5.86503 60 0.34 0.03 5.87 4.71 0.99 0.62 108.91 314 2.62 297 850141044 0.37 0.99 54.97 80.3 0.39 0.21 0 0 good 0.62 81.5 0 -0.01 0
951771438 4.19388 60 0.07 0.14 4.19 6.19 1 0.81 170.92 315 4.13 298 850141046 0.3 0.99 53.06 111.51 0.54 0.18 0 0 good 0.34 86.73 0 -0.03 0
951771443 1.38098 70 -0.82 -0.09 1.38 3.62 0.94 0.47 60.96 316 1.73 299 850141046 0.61 0.99 52.23 346.53 0.2 0.16 0.11 0 good 0 56.9 0 -0.04 0.08
951771449 1.79143 60 -3.78 0.08 1.79 4.53 0.98 0.56 59.41 317 1.32 300 850141046 8.71 0.91 63.5 929.37 0.14 0.22 0.5 0 good 0.21 76.52 0 -0.01 0.41
951771453 3.01431 70 0.76 0.09 3.01 4.1 0.96 0.85 67.06 318 2.15 301 850141050 0.57 0.99 44.93 353.33 0.15 0.25 0.04 0 good 1.03 66.12 0 -0.01 0.21
951771458 1.86583 40 15.11 0.06 1.87 3.95 0.92 0.54 72.36 319 1.86 302 850141044 5.35 0.95 55.94 499.53 0.28 0.21 0.5 0 good -7.9 61.71 0 -0.02 0.33
951771465 0.02914 40 0.69 nan 0.03 3.63 0.33 0.63 250.64 320 4.84 303 850141050 0.38 0.74 1.61 0 0.76 0.12 0.5 0 noise 0.69 30.56 0.01 -0.09 0
951771471 0.03493 50 2.06 nan 0.03 5.64 0.42 0.14 101.57 321 3.05 304 850141048 1.33 0.53 10.13 5 0.28 0.1 0.42 0 noise 0 53 0 -0.17 0
951771477 0.35723 50 -1.72 0.17 0.36 3.31 0.85 0.77 149.9 322 3.49 305 850141052 0.21 0.86 25.21 81.57 0.49 0.19 0.02 0 good 0.34 41.25 0.01 -0.02 0
951771483 0.86812 90 -0.08 0.06 0.87 3.76 0.79 0.92 45.22 323 1.32 306 850141052 0.23 0.99 53.42 601.09 0.08 0.4 0.02 0 good 3.71 41.42 0.01 -0 0
951771488 2.25034 100 0.88 0.04 2.25 3.63 0.85 0.91 43.01 324 1.28 307 850141062 0.39 0.99 47.07 409.74 0.07 0.32 0.05 0 good 2.75 53.99 0.01 -0.01 0.33
951771494 1.36796 70 -0.07 0.07 1.37 3.24 0.64 0.7 58.87 325 1.76 308 850141054 0.53 0.99 38.27 440.83 0.13 0.23 0.19 0 good 1.17 41.61 0.02 -0.03 0.21
951771499 1.9794 90 0.44 0.14 1.98 4.54 0.86 0.81 69.88 326 1.85 309 850141066 0.39 0.99 34.31 294.79 0.17 0.22 0 0 good 1.72 49.95 0.01 -0.03 0.06
951771507 2.54867 80 0.14 0.04 2.55 3.21 0.66 0.7 77.46 327 2.29 310 850141058 0.56 0.99 21.58 444.38 0.18 0.26 0.5 0.01 good 1.3 46.34 0.03 -0.04 0.11
951771512 4.34724 50 -0.34 0.08 4.35 2.93 0.74 0.6 89.45 328 2.63 311 850141058 0.35 0.99 28.04 228.15 0.29 0.18 0.24 0.02 good 1.37 54.02 0.03 -0.04 0.07
951771517 3.91891 10 nan 0.06 3.92 3.81 0.9 0.26 119.82 329 3.27 312 850141058 0.29 0.94 14.93 264.7 0.47 0.1 0.12 0 noise nan 55.2 0.02 -0.1 0.04
951771522 4.67925 70 0.27 0.05 4.68 4.34 0.95 0.62 96.59 330 3.06 313 850141060 0.69 0.99 49.94 162.5 0.21 0.18 0 0.01 good 0.89 76.97 0.01 -0.05 0.01
951771528 0.57196 60 0 -0.06 0.57 2.68 0.5 0.63 84.88 331 2.38 314 850141060 0.47 0.98 22.02 252.89 0.26 0.19 0.14 0 good 1.1 35.74 0.03 -0.03 1.18
951771533 0.68016 70 0.41 0.03 0.68 2.86 0.65 0.63 72.12 332 2.14 315 850141064 0.55 0.99 36.38 377.01 0.2 0.21 0.03 0 good 0.69 37.75 0.04 -0.02 0.84
951771538 2.74791 70 0.62 0.1 2.75 3.24 0.77 0.65 84.39 333 2.32 316 850141066 0.46 0.99 23.43 392.1 0.23 0.21 0.5 0.01 good 0.89 52.16 0.02 -0.03 0.22
951771543 2.02022 70 -0.14 0.05 2.02 2.49 0.71 0.54 72.74 334 1.99 317 850141066 0.53 0.99 34.82 260.88 0.22 0.25 0.5 0.01 good 0.69 43.36 0.03 -0.03 0.18
951771547 4.78693 90 -0.21 0.03 4.79 3.96 0.93 0.27 104.8 335 2.68 318 850141066 0.56 0.99 57.39 136.83 0.48 0.18 0.01 0 good -0.14 58.34 0.01 -0.07 0.18
951771552 2.32061 170 0.48 0.02 2.32 2.17 0.42 0.54 63.41 336 1.52 319 850141068 0.41 0.99 37.01 503.04 0.18 0.25 0.5 0.01 noise 0.27 35.76 0.08 -0.03 1.37
951771558 6.86873 80 -0.96 0.06 6.87 3.21 0.9 0.32 78.18 337 2.21 320 850141068 0.42 0.99 53.38 168.63 0.32 0.15 0.38 0.02 good 0 63.3 0.02 -0.05 0.86
951771563 0.11915 30 -15.11 nan 0.12 6.14 0.98 0.16 127.08 338 3.4 321 850141068 0.73 0.7 13.25 145.62 0.42 0.07 0.05 0 good 9.61 66.5 0 -0.27 0
951771568 0.00651 150 0.29 nan 0.01 4.59 0 0.7 91.8 339 2.47 322 850141068 0.34 0.44 nan 0 0.27 0.19 0.5 0 good 0.82 52.35 0 -0.02 0
951771572 2.39574 60 -0.27 0.06 2.4 3.12 0.66 0.56 77.69 340 2.31 323 850141074 0.36 0.99 28.44 415.38 0.25 0.21 0.11 0.01 good 1.03 52.49 0.01 -0.04 0.13
951771577 3.0018 60 -0.07 0.03 3 3.65 0.67 0.71 97.96 341 2.46 324 850141074 0.36 0.99 46.63 197.86 0.3 0.19 0.03 0.01 good 0.34 43.28 0.03 -0.03 0.19
951771583 5.8083 120 0.62 0.1 5.81 3.41 0.86 0.66 76.43 342 2.26 325 850141076 0.6 0.99 39.86 244.72 0.2 0.19 0.06 0.01 good 1.49 57.7 0.01 -0.03 0.16
951771588 5.41314 70 0 0.05 5.41 3.84 0.82 0.66 89.5 343 2.6 326 850141076 0.56 0.99 46.7 210.68 0.25 0.19 0.03 0.01 good 0.21 48.49 0.02 -0.02 0.09
951771594 3.27368 80 -0.27 0.04 3.27 3.03 0.79 0.66 66.49 344 2.01 327 850141078 0.55 0.99 41.74 273.71 0.18 0.21 0.19 0 good 0.76 48.8 0.01 -0.02 0.23
951771601 5.52867 100 0.34 0.09 5.53 4.5 0.98 0.76 79.88 345 2.09 328 850141080 0.37 0.99 43.89 136.55 0.23 0.16 0 0 good 0.65 63.43 0 -0.04 0.01
951771607 1.00194 80 0.34 0 1 4.88 0.96 0.6 159.02 346 3.64 329 850141080 0.43 0.99 50.23 181.3 0.43 0.15 0 0 good 0.51 68.15 0 -0.06 0
951771613 4.61436 80 -0.21 0.06 4.61 2.79 0.84 0.52 66.32 347 1.86 330 850141082 0.44 0.99 38.27 187.31 0.21 0.27 0.46 0.01 good 0.89 58.06 0.01 -0.04 0.04
951771620 6.89674 50 0.34 0.17 6.9 3.51 0.92 0.67 160.72 348 3.98 331 850141082 0.43 0.99 57.56 135.46 0.44 0.21 0 0 good 0.34 52.74 0.01 -0.08 0.05
951771626 1.36703 70 0.41 0.03 1.37 3.72 0.62 0.71 100.04 349 2.69 332 850141084 0.33 0.99 36.94 343.36 0.31 0.21 0.03 0 good 0.69 34.92 0.02 -0.01 0.21
951771633 2.41093 150 0.42 0.06 2.41 2.21 0.27 0.65 81.98 350 1.86 333 850141084 0.62 0.99 29.09 438.9 0.17 0.3 0.47 0 good 1 28.33 0.11 -0.03 0.43
951771639 11.5399 60 0.21 0.06 11.54 3.16 0.82 0.91 64.46 351 1.83 334 850141084 0.42 0.99 52.79 199.92 0.14 0.25 0.33 0.01 good 0.69 62.55 0.01 -0.01 0.02
951771645 4.6558 150 0.52 0.04 4.66 2.37 0.46 0.63 63.62 352 1.7 335 850141084 0.65 0.99 37.9 333.44 0.13 0.34 0.5 0.01 good 0.61 37.17 0.04 -0.02 0.27
951771652 5.98996 70 0.62 0.07 5.99 2.76 0.69 0.65 87.65 353 2.32 336 850141086 0.62 0.99 42.88 268.46 0.25 0.19 0.12 0.01 good 0.69 44.45 0.02 -0.04 0.19
951771658 11.5414 100 -0.06 0.03 11.54 2.04 0.85 0.65 76.42 354 2.06 337 850141086 0.68 0.99 31.94 177.29 0.17 0.29 0.17 0.01 good 1.1 57.41 0.01 -0.03 0.05
951771665 8.46951 80 -0.14 0.08 8.47 4.02 0.92 0.6 146.77 355 3.26 338 850141090 0.45 0.99 44.75 161.3 0.33 0.26 0 0 good 0.62 51.23 0.02 -0.06 0.04
951771670 13.1894 130 0.76 0.07 13.19 2.54 0.84 0.74 61.64 356 1.69 339 850141088 0.57 0.99 42.87 224.82 0.12 0.29 0.26 0.02 good 1.1 57.3 0.02 -0.02 0.02
951771676 9.0145 90 -0.27 0.03 9.01 4.72 0.97 0.22 103.94 357 2.23 340 850141088 0.69 0.99 43.67 168.7 0.41 0.12 0.02 0 good 0.37 62.04 0 -0.13 0.04
951771684 18.1031 60 0.07 0.05 18.1 3.07 0.84 0.71 92.22 358 1.84 341 850141090 0.53 0.99 35.54 148.23 0.15 0.36 0.03 0.01 good 4.81 60.78 0.03 -0.05 0.07
951771690 10.0666 60 0 0.04 10.07 2.1 0.7 0.7 123.31 359 2.45 342 850141090 0.41 0.99 54.73 205.83 0.29 0.23 0.05 0.01 good 2.75 42.06 0.05 -0.04 0.08
951771697 5.62436 30 0 0.17 5.62 4.33 0.92 0.59 139.63 360 3.15 343 850141092 0.4 0.99 40.27 174.87 0.38 0.22 0.01 0 good nan 49.84 0.01 -0.06 0.03
951771701 7.59312 70 0.65 0.07 7.59 3.46 0.8 0.65 85.55 361 2.15 344 850141092 0.46 0.99 52.04 220.33 0.2 0.29 0.18 0.01 good 1.72 52.28 0.01 -0.04 0.16
951771706 2.95881 100 0.69 0.31 2.96 8.45 1 0.63 191.32 362 4.24 345 850141092 0.47 0.98 36.13 97.04 0.43 0.23 0 0 good 1.17 131.6 0 -0.09 0
951771712 19.8755 70 -1.03 0.11 19.88 3.41 0.84 0.63 131.92 363 2.91 346 850141098 0.5 0.99 35.6 112.93 0.33 0.26 0.06 0.02 good 0.27 58.04 0.03 -0.07 0.22
951771718 2.07374 80 0.48 0.14 2.07 5.48 0.95 0.73 192.23 364 3.87 347 850141098 0.34 0.99 37.74 132.35 0.59 0.18 0 0 good 0.89 55.52 0 -0.06 0.03
951771724 8.25695 30 nan 0.02 8.26 2.26 0.73 0.62 80.15 365 1.84 348 850141098 0.43 0.99 28.44 269.51 0.19 0.27 0.13 0.01 good -0.34 46.64 0.02 -0.02 0.08
951771730 4.56145 150 0.39 0.05 4.56 1.91 0.33 0.63 70.37 366 1.73 349 850141096 0.5 0.99 34.54 355.19 0.13 0.32 0.5 0.01 good 1.08 33.72 0.06 -0.03 0.32
951771735 14.1265 120 0.61 0.05 14.13 2.53 0.9 0.85 74.26 367 1.92 350 850141102 0.3 0.99 42.31 155.56 0.18 0.27 0.18 0.02 good 1.59 62.66 0.01 -0.01 0.05
951771742 4.94235 50 -2.06 0.04 4.94 4.92 1 0.34 177.86 368 2.91 351 850141102 0.69 0.99 46.62 68.8 0.59 0.23 0 0 good 0.62 66.73 0 -0.15 0
951771747 6.43018 160 0.36 0.04 6.43 3.35 0.92 0.6 68.37 369 2.02 352 850141104 0.23 0.99 41.43 221.1 0.19 0.22 0.01 0.01 good 1.29 59.1 0.01 -0.02 0.07
951771753 1.40289 90 0.55 0.15 1.4 4.08 0.95 0.87 131 370 3.41 353 850141104 0.33 0.99 46.4 117.24 0.36 0.21 0 0 good 0.89 52.1 0 -0.05 0.1
951771759 0.84095 90 -0.69 0.06 0.84 4.07 0.88 0.78 120.73 371 3.2 354 850141104 0.36 0.99 49.23 216.17 0.33 0.23 0 0 good 0.56 48.47 0 -0.04 0.05
951771764 0.37914 70 0.34 -0.02 0.38 3.73 0.68 0.76 91.99 372 2.48 355 850141104 0.33 0.99 35.52 197.3 0.27 0.21 0.01 0 good 0.96 41.47 0 -0.03 0
951771771 2.218 70 0 0.01 2.22 4.81 0.99 0.81 127.12 373 2.6 356 850141106 0.47 0.99 44.95 166.96 0.28 0.21 0 0 good 0.96 59.74 0 -0.03 0.01
951771777 3.94567 100 0.82 0.09 3.95 2.11 0.67 0.67 86.38 374 2.05 357 850141106 0.55 0.99 38.97 314.49 0.21 0.26 0.42 0.01 good 0.78 37.98 0.06 -0.02 0.26
951771782 9.33443 50 0.69 0.08 9.33 3 0.81 1.04 95.33 375 2.26 358 850141106 0.31 0.99 38.99 138.12 0.27 0.21 0.06 0.02 good 0.69 46.8 0.04 -0.02 0.21
951771788 3.70903 70 1.03 0.08 3.71 3.14 0.67 0.74 114.61 376 2.53 359 850141106 0.46 0.99 52.89 236.87 0.33 0.23 0.02 0.01 noise 0.55 37.95 0.04 -0.03 0.72
951771794 2.83161 70 -0.82 0.09 2.83 3.63 0.66 0.84 87.83 377 2.37 360 850141108 0.51 0.99 37.07 261.88 0.22 0.19 0.5 0.01 good 0.82 41.02 0.03 -0.04 0.45
951771800 3.41215 110 -1.24 0.09 3.41 4.56 0.95 0.36 98.23 378 2.71 361 850141108 0.71 0.99 40.06 163.95 0.38 0.18 0.01 0 good 1.18 62.44 0 -0.07 0.07
951771806 3.12219 80 -0.76 0.09 3.12 3.9 0.8 0.85 72.68 379 2.21 362 850141108 0.47 0.9 26.51 282.13 0.18 0.22 0.39 0.01 good 1.03 62.21 0 -0.03 0.15
951771813 1.75506 60 0.14 0.21 1.76 3.98 1 0.44 118.82 380 3 363 850141112 0.44 0.99 50.28 96.35 0.36 0.18 0 0 good 0.34 92.07 0 -0.06 0
951771818 3.30881 70 -0.34 0.03 3.31 3.06 0.77 0.78 66.51 381 1.29 364 850141106 0.45 0.99 36.46 307.27 0.19 0.23 0.04 0 good 0.96 44.94 0.02 -0.01 0.55
951771824 6.21451 70 -1.03 0.07 6.21 3.97 0.91 0.32 82.43 382 2.17 365 850141114 0.55 0.99 39.69 174.84 0.36 0.19 0.14 0.01 good 0.14 74.07 0.01 -0.07 0.06
951771831 2.3697 70 0 0.07 2.37 3.26 0.89 0.41 78.32 383 2.16 366 850141114 0.64 0.99 39.76 213.62 0.26 0.3 0.07 0 good 0.27 53.29 0.01 -0.05 0.1
951771837 3.87396 150 0.64 0.04 3.87 2.67 0.54 0.77 56.01 384 1.21 367 850141108 0.69 0.99 35.04 469.14 0.09 0.32 0.5 0 noise 1.05 40.39 0.03 -0.02 0.27
951771844 2.08521 90 0.33 0.1 2.09 3.77 0.9 0.71 67.62 385 1.85 368 850141116 0.67 0.99 15.75 485.38 0.19 0.21 0.5 0 good 0.82 54.34 0.01 -0.01 0.77
951771850 3.78664 50 0.34 0.1 3.79 4.26 0.99 0.99 100.12 386 2.42 369 850141118 0.25 0.99 37.56 127.65 0.33 0.19 0 0 good 1.03 71.48 0 -0.03 0
951771856 1.62589 70 -0.06 0.03 1.63 3.88 0.82 0.66 95.83 387 2.41 370 850141122 0.45 0.99 32.59 388.97 0.29 0.21 0.04 0 good 1.37 49.06 0.01 -0.02 0.59
951771862 2.99746 80 0.07 0.08 3 3.21 0.79 0.37 80.96 388 2.19 371 850141122 0.87 0.99 27.33 268.73 0.31 0.23 0.4 0.01 good -0.48 53.97 0.02 -0.06 0.69
951771866 0.01044 50 -0.34 nan 0.01 6.27 0 0.63 87.65 389 2.65 372 850141124 0.33 0.51 nan 0 0.29 0.22 0.22 0 good 0.34 67.83 0 -0.03 0
951771872 1.64263 70 0.55 0.07 1.64 4.52 0.93 0.87 74.41 390 2.14 373 850141126 0.35 0.99 24.73 410.63 0.21 0.19 0.1 0 good 2.06 58.75 0 -0.03 0.32
951771878 4.61539 110 -0.32 0.08 4.62 3.83 0.94 0.37 51.33 391 1.5 374 850141132 0.7 0.99 38.07 304.99 0.21 0.25 0.5 0.01 good -0.07 58.28 0.01 -0.04 0.76
951771885 4.81121 60 -1.37 0.1 4.81 5.43 0.98 0.3 89 392 2.6 375 850141132 0.59 0.99 44.6 165.13 0.41 0.16 0.01 0 good 0.69 71.72 0 -0.07 0.05
951771892 0.48216 60 1.37 -0.06 0.48 3.43 0.42 0.74 74.88 393 2.03 376 850141132 0.47 0.99 30.59 375.53 0.2 0.23 0.45 0 noise 1.03 32.2 0.06 -0.02 1.17
951771898 21.6197 50 -2.4 0.11 21.62 4.38 1 0.81 59.68 394 2.12 377 850141136 0.41 0.99 21.19 151.36 0.1 0.3 0.01 0.02 good 0.34 110.96 0 -0.02 0.01
951771904 3.51838 110 0.52 0.05 3.52 2.15 0.56 0.6 42.14 395 1.18 378 850141138 0.46 0.99 69.15 598.12 0.15 0.15 0.5 0.01 noise 0.34 39.47 0.08 -0.01 0.5
951771910 12.4171 70 -1.51 0.12 12.42 3.95 0.98 1.58 70.49 396 2.26 379 850141138 1.02 0.99 37.41 116.34 0.06 0.52 0 0.01 good -1.37 73.81 0 -0.02 0.02
951771918 8.58276 70 -0.82 0.07 8.58 3.88 0.94 0.29 95.36 397 2.91 380 850141138 0.96 0.99 38.6 152.29 0.42 0.19 0.01 0.01 good -0.34 67.59 0.01 -0.15 0.06
951771924 1.99087 90 0.25 0.07 1.99 3.41 0.79 0.82 65.47 398 1.93 381 850141138 0.45 0.99 14.76 284.18 0.17 0.23 0.5 0 noise 1.37 43.75 0.03 -0.01 0.46
951771931 10.2836 50 -0.48 0.1 10.28 4.27 0.95 0.25 90.44 399 2.83 382 850141146 0.58 0.99 22.91 184.36 0.4 0.16 0.04 0.01 good nan 72.34 0.01 -0.07 0.29
951771938 2.95086 50 0.76 0.07 2.95 5.64 1 1.07 65.51 400 2.16 383 850141148 0.24 0.99 31.84 314.48 0.16 0.27 0.03 0 good nan 56.93 0.01 -0.01 0.19
951771944 3.20909 90 0.02 0.06 3.21 nan nan 2.06 38.97 401 1.08 384 850141198 2.62 0.99 53.3 901.21 0.05 0.49 0.35 0 noise nan nan nan nan 7.69
951771951 0.93333 90 0.1 0.32 0.93 2.57 0.8 1.33 80.14 402 2.13 385 850141198 1.14 0.97 21.63 415.89 0.07 0.58 0 0.02 noise nan 24.44 0.18 -0.02 13.12
951771958 7.62329 90 0.3 0.1 7.62 2.45 0.97 1.28 31.48 403 1.13 386 850141198 1.21 0.99 30.55 577.86 0.01 0.99 0.46 0.3 noise nan 343.63 0.06 -0.01 0.93
951771965 5.10593 90 0.15 0 5.11 3.71 0.98 0.92 36.98 404 1.24 387 850141198 1.39 0.99 37.44 835.28 0.03 0.84 0.5 0 noise nan 71.32 0 -0.02 1.03
951771971 0.51761 60 -1.03 -0.04 0.52 4.09 0.74 0.29 166.56 405 2.9 388 850140516 0.44 0.99 33.89 248.25 0.67 0.14 0.02 0 good 0 42.49 0 -0.1 0.43
951771979 0.03338 50 0.69 nan 0.03 7.37 0 0.4 196.61 406 4.1 389 850140536 0.9 0.49 12.52 12.07 0.45 0.21 0.11 0 good -1.03 50.33 0 -0.04 0
951771985 0.17319 120 0.14 nan 0.17 5.38 0.47 0.25 236.38 407 1.9 390 850140566 0.4 0.93 33.6 178.06 0.91 0.11 0.05 0 noise -1.45 50.15 0 -0.02 2.58
951771992 39.7843 60 0 0.08 39.78 5.16 0.99 0.26 223.61 408 3.54 391 850140586 0.45 0.99 36.48 113.26 0.99 0.14 0 0.01 good -0.34 134.28 0 -0.18 0
951771998 0.24522 140 -0.6 nan 0.25 2.59 0.15 0.34 161.77 409 1.78 392 850140586 0.34 0.95 27.06 379.48 0.67 0.18 0.01 0 good -0.47 17.64 0.08 -0.04 0
951772005 0.33904 70 -0.41 nan 0.34 5.1 0.77 0.19 279.14 410 3.65 393 850140602 0.43 0.99 17.8 247.33 1.16 0.12 0.01 0 good -0.07 43.94 0 -0.32 0.34
951772012 0.12359 60 -0.89 -0.01 0.12 3.45 0.25 0.18 260.02 411 3.28 394 850140626 0.69 0.74 10.15 2.72 1.02 0.1 0.04 0 good 0.34 29.08 0.02 -0.3 0
951772018 0.21732 50 0 0.03 0.22 6.06 0.08 0.63 324.08 412 4.82 395 850140648 1 0.45 15.33 98.84 0.6 0.19 0.03 0 good 0 30.69 0 -0.02 1.64
951772026 33.3255 70 0.31 0.1 33.33 4.16 0.99 1.63 131.28 413 0.64 396 850140654 1.24 0.99 34.39 120.33 0.02 0.73 0.2 0 good -2.06 93.86 0 nan 0
951772032 1.78823 60 0 0.04 1.79 3.9 0.91 0.51 166.78 414 2.62 397 850140648 1.06 0.57 25.89 180.25 0.31 0.18 0 0 good -0.27 58.25 0 -0.01 0.24
951772037 0.07182 60 0 nan 0.07 4.77 0.5 0.16 290.25 415 1.92 398 850140654 0.76 0.21 16.06 44.11 0.46 0.11 0.48 0 good 0.69 50.45 0 -0.15 15.02
951772045 0.15562 70 0 nan 0.16 7.27 0.9 0.16 140.99 416 3.76 399 850140696 0.57 0.4 18.73 107.89 0.53 0.08 0.01 0 good 0.69 63.56 0 -0.19 1.6
951772049 0.10788 70 -0.07 -0.01 0.11 5.58 0.64 0.16 116.52 417 2.88 400 850140696 0.61 0.53 16.65 60.98 0.44 0.1 0.01 0 good 0.69 46.48 0 -0.16 0
951772057 0.034 120 -0.69 nan 0.03 3.99 0.04 0.21 69.95 418 1.05 401 850140692 0.65 0.55 29.47 28.04 0.2 0.11 0.31 0 good 0.62 33.03 0.01 -0.05 0
951772063 0.91008 50 -0.07 0.2 0.91 4.38 0.94 0.25 194.59 419 4.03 402 850140698 0.52 0.99 36.71 163.11 0.85 0.14 0 0 good -0.69 46.38 0.02 -0.2 0.09
951772073 0.28097 20 -0.69 0.04 0.28 4.14 0.78 0.23 204.08 420 4.68 403 850140698 0.33 0.9 30.45 84.3 0.9 0.11 0.01 0 good nan 48.34 0 -0.08 0
951772078 0.31662 70 -0.69 nan 0.32 4.33 0.64 0.36 102.49 421 3.29 404 850140722 0.53 0.99 21 193.25 0.43 0.15 0.02 0 good 0.62 36.83 0.03 -0.08 6.18
951772083 0.86719 60 -2.34 0.16 0.87 7.2 0.98 0.81 126.47 422 2.03 405 850140826 0.21 0.99 10.39 306.91 0.47 0.16 0.03 0 good 0.34 56.23 0 -0.04 2.42
951772090 2.37993 50 -0.69 0.09 2.38 4.87 0.95 0.48 112.12 423 1.75 406 850140850 0.47 0.99 11.88 146.07 0.39 0.19 0.01 0.01 good 0.69 65.08 0 -0.06 0.31
951772095 0.09941 90 -0.59 nan 0.1 2.71 0 0.81 177.61 424 2.02 407 850141004 0.38 0.85 24.69 40.69 0.67 0.18 0.06 0 good 1.03 16.15 0.2 -0.04 7.84
951772101 0.46284 70 0.14 0.08 0.46 3.94 0.4 0.65 136.21 425 3.53 408 850141074 0.39 0.92 28.77 209.27 0.4 0.21 0 0 good 0.69 29.89 0.03 -0.06 0.36
951772107 0.80612 60 -1.03 0.03 0.81 5.26 0.57 0.67 143.95 426 3.69 409 850141074 0.39 0.95 30.19 146.41 0.42 0.18 0 0 good 0.41 49.9 0 -0.06 0.06
951772113 0.5328 60 0.34 nan 0.53 4.96 0.62 0.76 71.21 427 2.08 410 850141108 0.44 0.87 16.51 287.7 0.2 0.18 0.28 0 good 1.92 43.09 0 -0.01 0.27
951772119 0.14643 90 0.13 nan 0.15 3.4 0.8 1.41 146.59 428 2.66 411 850141198 1.04 0.92 15.62 66.31 0.12 0.55 0.07 0 noise nan 16.42 0.31 -0.11 72.26
951772125 0.06965 80 0.65 nan 0.07 3.39 0 0.16 116.35 429 1.93 412 850140648 0.75 0.5 68.31 64.24 0.45 0.1 0.33 0 good -1.03 28.97 0.01 -0.19 0
951772131 0.08639 70 0 nan 0.09 6.87 0.99 0.18 142.38 430 2.57 413 850140692 0.82 0.34 13.18 61.49 0.41 0.08 0.01 0 good 0.62 71.21 0 -0.15 0
951772137 0.05384 50 0.27 nan 0.05 6.9 0.76 0.21 126.68 431 3.36 414 850140702 0.73 0.39 13.2 60.24 0.4 0.12 0.08 0 good nan 47.99 0 -0.05 0
951772142 0.03472 70 -0.07 nan 0.03 5.38 0.48 0.16 136.61 432 3.43 415 850140696 0.63 0.28 20.18 12.36 0.52 0.08 0.04 0 good 0.69 41.59 0 -0.19 0
951772147 0.61784 70 -0.14 0.09 0.62 4.84 0.72 0.21 188.29 433 2.86 416 850140636 0.59 0.99 62.09 246.17 0.81 0.14 0.03 0 good 0 36.58 0.01 -0.19 3.65
951772153 0.04557 70 -1.72 nan 0.05 4.22 0.21 0.78 124.87 434 1.96 417 850140826 0.23 0.85 7.7 3.89 0.46 0.14 0.5 0 good -0.62 30.92 0.03 -0.04 0
951772159 0.24501 90 -1.1 0.04 0.25 4.17 0.33 0.88 214.78 435 2.5 418 850140992 0.28 0.98 38.21 80.32 0.64 0.18 0 0 good -0.27 30.69 0.01 -0.04 1.29
951772221 4.70457 70 nan nan 4.7 3.14 0.53 0.52 46.17 0 4.04 0 850136298 0.77 0.99 23.87 140.42 1.26 0.22 0 0.02 good 5.99 17.05 0.07 -0.2 0.12
951772227 3.72102 80 nan 0.02 3.72 2.6 0.27 0.51 41.74 1 3.35 1 850136298 0.94 0.99 20.23 296.37 0.99 0.21 0 0.03 good 0.3 16.59 0.06 -0.17 0.63
951772233 4.29154 80 nan 0.01 4.29 2.39 0.4 0.56 56.95 2 3.46 2 850136298 0.91 0.99 15.74 166.59 0.94 0.23 0.03 0.02 good -0.19 15.37 0.08 -0.17 0.51
951772239 2.28093 70 nan 0.06 2.28 2.07 0.67 1.26 73.74 3 2.14 3 850136298 1.3 0.99 17.86 412.16 0.14 0.73 0.5 0 noise -0.44 17.97 0.04 -0.02 0.6
951772247 4.57168 80 nan 0.02 4.57 2.46 0.32 1.55 40.76 4 2.83 4 850136298 1.06 0.99 50.01 411.17 0.19 0.65 0.29 0.03 noise 1.76 17.74 0.06 nan 0.59
951772253 3.104 80 nan 0.01 3.1 2.15 0.34 1.57 29.47 5 2.07 5 850136298 1.29 0.99 28.4 290.02 0.14 0.78 0.11 0.02 noise 0.01 18.45 0.04 nan 0.86
951772260 3.12601 80 nan -0.04 3.13 2.47 0.24 0.8 38.28 6 2.56 6 850136298 0.87 0.99 39.38 444.41 0.72 0.22 0.16 0.02 good 3.82 14.18 0.08 -0.07 0.59
951772266 0.01395 80 nan nan 0.01 2.99 0 0.51 54.35 7 1.51 7 850136298 0.87 0.57 nan 0 1.02 0.16 0.5 0 good -0.99 7.83 0.03 -0.07 0
951772273 9.67812 30 nan 0.29 9.68 3.87 0.97 0.44 255 8 3.24 8 850136302 0.8 0.99 10.06 158.49 0.97 0.14 0.02 0 good 0 56.93 0 -0.18 0.01
951772280 3.65292 50 nan 0.11 3.65 2.59 0.77 1.07 138.59 9 1.33 9 850136298 1.73 0.99 27.74 361.21 0.06 0.93 0.5 0 good -0.14 30.39 0.01 -0.02 0.24
951772286 5.45903 50 -0.69 0.07 5.46 2.33 0.72 0.6 178.14 10 1.43 10 850136310 0.96 0.99 39.5 270.14 0.39 0.26 0.5 0.01 good 0.34 36.77 0.01 -0.07 0.16
951772293 0.12597 70 -0.69 nan 0.13 2.59 0 0.56 242.04 11 2.24 11 850136308 0.52 0.66 17.05 33.28 0.68 0.26 0.49 0 good 0.22 19.38 0.03 -0.12 0
951772298 6.74628 30 -0.69 0.34 6.75 5.27 0.99 0.47 693.28 12 5.53 12 850136306 0.4 0.99 30.98 53.88 2.49 0.16 0 0 good 1.37 59.46 0 -0.37 0
951772304 10.3528 50 0.69 0.06 10.35 3.44 0.94 0.45 332.26 13 3.85 13 850136306 0.47 0.99 37.8 119.84 1.07 0.19 0 0 good 0.07 60.35 0 -0.21 0.06
951772310 1.77521 50 -0.69 -0.02 1.78 2.38 0.39 0.54 194.6 14 1.96 14 850136306 0.49 0.99 41.33 245.98 0.54 0.27 0.1 0 noise -0.21 24.2 0.03 -0.09 0.42
951772316 10.7254 30 -0.69 0.2 10.73 3.35 0.84 0.47 222.7 15 2.11 15 850136308 0.44 0.99 22.51 219.62 0.75 0.22 0.12 0.01 good 1.37 60.04 0.01 -0.1 0.2
951772322 8.32804 40 0 0.09 8.33 3.28 0.76 0.43 391.21 16 3.78 16 850136308 0.46 0.99 23.57 127.51 1.38 0.22 0 0.01 good -0.34 39.09 0.03 -0.23 0.08
951772328 6.40651 60 -1.37 0.09 6.41 2.98 0.81 0.47 267.17 17 2.34 17 850136308 0.35 0.99 41.97 236.11 0.85 0.22 0.03 0 good -0.27 42.11 0.01 -0.1 0.11
951772334 18.4867 50 -0.69 0.05 18.49 4.02 0.97 0.38 330.37 18 3.07 18 850136308 0.35 0.99 39.23 149.84 1.25 0.19 0 0 good 0.14 64.04 0.01 -0.15 0.02
951772340 5.77689 50 -0.69 -0 5.78 2.36 0.75 0.51 260.99 19 2.7 19 850136308 0.46 0.99 32.63 233.83 0.85 0.23 0.14 0.01 noise 0.21 40.31 0.02 -0.14 0.21
951772344 0.73565 50 -1.37 0.16 0.74 2.48 0.59 0.48 316.68 20 2.55 20 850136308 0.46 0.99 22.83 350.41 0.98 0.25 0.03 0 noise 0.62 24.52 0.06 -0.12 0.21
951772351 2.77353 40 -0.69 0.04 2.77 2.52 0.24 0.55 276.62 21 2.62 21 850136308 0.47 0.99 28.85 367.24 0.81 0.26 0.22 0 good 0.69 23.15 0.05 -0.12 0.25
951772355 15.4752 60 0 0.23 15.48 4.42 1 0.78 297.06 22 2.77 22 850136312 1.63 0.99 41.47 420.56 0.56 0.1 0.14 0 good -5.97 104.86 0 -0.39 0.08
951772361 15.1415 60 -0.34 0.15 15.14 7.05 1 0.45 417.76 23 3.95 23 850136314 0.37 0.99 38.97 89.6 1.43 0.21 0 0 good -0.21 131.63 0 -0.22 0
951772367 13.1557 60 0.34 0.17 13.16 4.01 0.99 0.44 483.22 24 4.15 24 850136314 0.47 0.99 40.48 89.6 1.66 0.22 0 0 good 1.03 82.38 0 -0.31 0
951772373 9.70323 60 -0.62 0.03 9.7 2.83 0.89 0.51 199.58 25 1.82 25 850136314 0.38 0.99 43.02 215.69 0.55 0.29 0.04 0.01 good 0 73.83 0 -0.12 0.04
951772379 7.98435 70 -0.69 0.04 7.98 2.85 0.88 0.49 213.51 26 2.2 26 850136314 0.37 0.99 47.19 198.18 0.7 0.29 0.07 0 good 0.14 63.74 0.01 -0.1 0.07
951772385 12.4186 60 1.03 0.09 12.42 3 0.98 0.44 292.2 27 2.54 27 850136314 0.41 0.99 37.93 119.4 1.05 0.22 0 0 good 0.41 63.56 0.01 -0.17 0.01
951772391 3.13418 80 -0.41 0.13 3.13 2.85 0.64 0.44 171.55 28 2.36 28 850136316 0.57 0.99 39.09 251.3 0.58 0.16 0.27 0 good 0.07 40.76 0.01 -0.09 0.26
951772397 11.6179 70 -1.37 0.17 11.62 4.62 0.96 0.54 287.76 29 2.5 29 850136308 0.44 0.99 40.38 102.61 0.9 0.23 0 0 good -0.24 55.79 0.01 -0.13 0.01
951772402 11.3955 60 -0.34 0.15 11.4 4.03 0.95 0.16 140.23 30 2.2 30 850136316 0.28 0.99 24.43 284.49 0.51 0.1 0.45 0 good -0.07 92.85 0 -0.09 0.08
951772407 2.20756 80 -0.14 0.06 2.21 2.84 0.6 0.51 122.8 31 1.9 31 850136316 0.61 0.99 40.05 325.98 0.37 0.23 0.5 0 noise -0.14 40.01 0.01 -0.07 0.29
951772413 10.3179 70 -0.21 0.05 10.32 3.79 0.92 0.49 192.3 33 2.2 32 850136320 0.61 0.99 34.96 118.43 0.66 0.18 0.01 0.01 good -0.21 61.75 0.01 -0.08 0.1
951772419 1.6946 100 -0.35 0.01 1.69 2.72 0.35 0.55 179.94 34 2.06 33 850136324 0.25 0.99 33.78 381.04 0.49 0.32 0.5 0 good -0.07 30.41 0.02 -0.08 0.38
951772428 10.7328 60 -0.41 0.26 10.73 5.99 0.99 0.45 394.63 35 5.06 34 850136322 0.41 0.99 39.4 79.17 1.31 0.21 0 0 good 0.34 94.94 0 -0.22 0
951772434 12.0966 60 -0.76 0.11 12.1 3.79 0.97 0.43 258.91 36 3.32 35 850136322 0.46 0.99 38.43 90.92 0.86 0.23 0.01 0 good 0.34 70.02 0 -0.17 0.02
951772441 5.97333 80 -0.69 0.07 5.97 3.45 0.89 0.54 169.32 37 2.02 36 850136322 0.46 0.99 8.33 163.87 0.45 0.34 0.36 0 good -0.41 61.99 0 -0.09 0.11
951772448 0.38296 80 -0.48 nan 0.38 2.49 0 0.45 159.08 38 1.64 37 850136322 0.54 0.99 34.64 376.71 0.45 0.29 0.44 0 good -0.14 24.04 0.03 -0.1 0
951772455 18.6347 60 0 0.11 18.63 4.84 0.92 0.44 315.58 39 3.6 38 850136324 0.43 0.99 34.34 120.11 1.06 0.23 0 0.01 good -0.07 71.15 0.01 -0.22 0.06
951772462 8.74727 70 -0.34 0.08 8.75 3.74 0.86 0.54 237.94 41 2.9 39 850136324 0.33 0.99 38.66 90.76 0.71 0.3 0 0.01 good 0 59.3 0.01 -0.13 0.14
951772468 1.84847 60 -0.27 0.01 1.85 2.89 0.44 0.48 190.13 43 1.53 40 850136328 0.88 0.99 24.8 201.79 0.48 0.18 0.5 0 noise 0.34 37.98 0.01 -0.08 0.51
951772475 9.45988 70 0.41 0.2 9.46 5.76 0.98 0.47 205.97 44 2.29 41 850136330 0.4 0.99 24.25 70.42 0.67 0.25 0 0 good 0.41 62.11 0 -0.11 0.02
951772482 7.84856 70 -0.55 0.11 7.85 3.48 0.97 0.43 134.17 45 2.09 42 850136326 0.61 0.99 19.76 151.89 0.49 0.16 0.35 0 good -0.21 74.49 0 -0.08 0.11
951772489 0.06582 90 -0.07 nan 0.07 2.92 0 0.44 274.88 46 2.34 43 850136328 0.44 0.88 13.73 49.9 1.1 0.15 0.38 0 good 0.34 25.33 0.01 -0.09 17.88
951772495 11.0722 70 -0.27 0.18 11.07 4.22 0.89 0.43 333.07 48 3.77 44 850136330 0.48 0.99 33.37 69.28 1.12 0.26 0 0 good 0.07 46.56 0.02 -0.2 0.06
951772502 2.96905 100 -0.34 0.17 2.97 2.73 0.16 0.49 172.9 49 0.93 45 850136330 0.5 0.99 76.64 389.89 0.26 0.36 0.12 0.01 good 0.32 24.09 0.05 -0.07 0.14
951772509 17.9442 50 -0.34 0.11 17.94 2.63 0.66 0.45 250.36 50 3 46 850136330 0.59 0.99 15.7 71.42 0.79 0.25 0.42 0.02 good -0.34 55.85 0.02 -0.15 0.08
951772515 3.88615 80 0.08 0.06 3.89 2.5 0.17 0.49 223.09 51 2.56 47 850136330 0.47 0.99 29.49 182.83 0.64 0.27 0.31 0.01 noise 0 28.74 0.04 -0.12 0.36
951772523 4.55339 50 -0.69 0.06 4.55 2.22 0.67 0.51 135.08 52 1.62 48 850136330 0.38 0.99 22.68 128.49 0.33 0.32 0.01 0.01 noise 0.34 40.03 0.02 -0.05 0.32
951772529 14.0161 70 0 0.04 14.02 3 0.85 0.49 202.53 53 2.39 49 850136330 0.45 0.99 32.25 102.23 0.58 0.23 0.05 0.01 good 0.62 56.29 0.01 -0.13 0.08
951772535 6.00805 80 -0.21 0.19 6.01 2.82 0.97 0.96 226.21 54 1.68 50 850136332 2.12 0.99 29.92 163.99 0.14 1.4 0.5 0 good -0.14 75.53 0 -0 0.03
951772541 8.51777 60 -1.03 0.33 8.52 8.71 1 0.51 621.48 55 4.35 51 850136332 0.78 0.99 30.88 56.15 1.89 0.21 0 0 good 0.41 158.29 0 -0.32 0
951772548 8.34685 60 0.69 0.1 8.35 4.53 0.95 1.63 266.3 56 1.82 52 850136332 2.17 0.99 37.31 82.66 0.17 1.15 0 0 good 0.21 66.82 0 nan 0.1
951772555 3.23121 60 0 0.24 3.23 4.55 0.92 0.41 345.64 57 3.28 53 850136328 0.51 0.99 32.1 158.7 1.32 0.14 0 0 good 0.41 46.19 0.01 -0.18 0.29
951772561 0.59077 70 -0.07 0.16 0.59 4.73 0.81 0.19 125.85 58 1.78 54 850136334 0.35 0.88 11.64 165.55 0.52 0.11 0.5 0 good 0.48 52.49 0 -0.08 3.66
951772569 0.12566 50 -2.06 nan 0.13 3.09 0 0.47 293.73 59 2.19 55 850136330 0.42 0.76 16.57 55.94 1.19 0.18 0.5 0 noise -0.55 21.27 0.02 -0.19 9.84
951772576 11.8787 70 -0.07 0.11 11.88 4.7 0.99 0.96 210.71 60 1.42 56 850136332 2.25 0.99 31.99 88.43 0.14 1.9 0 0 good 0.48 84.01 0 -0.01 0.01
951772581 4.21889 90 -0.34 0.1 4.22 3.44 0.76 0.51 138.9 61 1.36 57 850136330 0.4 0.99 27.71 206.52 0.38 0.22 0.5 0 good -0.54 46.01 0.01 -0.09 0.2
951772589 7.18174 50 -1.03 0.08 7.18 2.41 0.74 0.44 269.89 62 2.48 58 850136330 0.73 0.99 39.16 111.94 0.69 0.27 0 0.01 good 0 35.53 0.03 -0.2 0
951772595 3.95766 60 0 0.09 3.96 4.43 0.93 0.48 192.12 63 2.47 59 850136338 0.34 0.99 30.31 127.29 0.57 0.25 0 0 good 0.62 43.35 0.01 -0.11 0.07
951772600 8.49968 70 0 0.07 8.5 4.1 0.95 0.36 133.28 64 2 60 850136338 0.27 0.99 25.2 128.75 0.53 0.18 0.35 0 good 0 73.49 0 -0.1 0.03
951772606 1.89136 90 0 0.08 1.89 3.14 0.88 0.47 125.7 65 1.73 61 850136338 0.32 0.99 27.51 280.21 0.4 0.23 0.5 0 good 0.14 53.92 0 -0.09 0.06
951772612 15.3178 70 0 0.06 15.32 4.29 0.95 1.52 277.23 66 1.77 62 850136332 2.01 0.99 38.11 70.66 0.16 1.85 0 0 good 0.21 79.07 0 -0.02 0.01
951772618 8.75554 60 -0.21 0.05 8.76 3.94 0.88 0.43 294.11 67 3.66 63 850136340 0.42 0.99 31.18 78.57 1.05 0.18 0 0 good 0 53.27 0.01 -0.19 0.07
951772623 4.32357 60 0 0.14 4.32 3.36 0.52 0.18 273.92 68 3.99 64 850136340 0.28 0.99 22.69 225.14 1.02 0.08 0.02 0.01 good 0.62 42.26 0.01 -0.25 0.07
951772630 2.79782 90 -0.27 0.1 2.8 3.49 0.88 0.45 172.5 69 2.21 65 850136340 0.41 0.99 16.29 221.19 0.56 0.21 0.5 0 good 0 58.15 0 -0.09 0.25
951772635 7.88483 70 -0.41 0.23 7.88 7.93 1 0.47 313.39 70 4.16 66 850136342 0.31 0.99 30.4 68.39 0.96 0.26 0 0 good 0.41 116.6 0 -0.19 0.01
951772640 19.2235 50 0 0.2 19.22 4.33 1 0.16 162.98 71 2.49 67 850136342 0.04 0.99 17.03 229.63 0.57 0.1 0.16 0 good 0.34 103.01 0 -0.13 0.01
951772647 11.4084 80 -0.96 0.24 11.41 4.82 0.99 1.58 194.91 72 2.02 68 850136344 1.04 0.99 30.07 70.5 0.09 0.67 0 0 good 0 97.31 0 -0.01 0.01
951772653 8.2618 80 0.14 0.13 8.26 3.29 0.95 0.44 189.82 73 1.98 69 850136344 0.85 0.99 25.28 118.17 0.72 0.14 0.04 0 good 0.62 68.56 0 -0.11 0.04
951772659 15.0126 50 1.03 0.16 15.01 4.29 0.69 0.41 179.42 74 2.68 70 850136346 0.29 0.99 21.25 74.5 0.61 0.29 0.08 0.03 good 0.34 73.61 0.02 -0.12 0.17
951772665 4.13767 60 -0.14 0.16 4.14 2.91 0.55 0.44 297.8 75 2.41 71 850136348 0.87 0.99 20.89 145.08 0.97 0.21 0.5 0 good 0.69 38.23 0.02 -0.18 0.12
951772671 7.32217 70 0 0.02 7.32 3.15 0.41 0.48 183.23 76 2.61 72 850136346 0.31 0.99 37.81 153.12 0.58 0.3 0.04 0.02 good 0 35.33 0.04 -0.11 0.14
951772678 2.33477 80 -0.34 0.07 2.33 2.98 0.29 0.45 172.74 77 2.25 73 850136346 0.3 0.99 23.32 274.43 0.54 0.32 0.26 0 good -0.33 26.5 0.06 -0.08 0.45
951772685 4.5414 70 0.69 -0 4.54 3.18 0.16 0.44 172.46 78 2.49 74 850136346 0.24 0.99 21.49 134.29 0.58 0.32 0.07 0.01 good 0.41 27.83 0.04 -0.07 0.27
951772690 14.0128 50 0.34 0.18 14.01 5.02 0.96 0.38 477.53 79 3.84 75 850136348 0.7 0.99 27.74 61.6 1.82 0.15 0 0 good 0.34 85.29 0 -0.32 0
951772696 10.392 60 0 -0 10.39 3.29 0.87 0.44 309.34 80 2.54 76 850136348 0.86 0.99 37.56 93.6 1.03 0.21 0.09 0.01 good 0.34 66.65 0.01 -0.19 0.28
951772703 0.6567 80 0.26 0.06 0.66 2.68 0.13 0.44 277.95 81 2.1 77 850136348 0.87 0.99 27.91 228.02 0.91 0.22 0.3 0 good 0.34 23.32 0.03 -0.15 0.45
951772710 1.17059 50 0.34 0.03 1.17 3.56 0.08 0.43 375.5 82 2.96 78 850136348 0.68 0.9 8.85 40.22 1.39 0.16 0.04 0 noise 0.34 29.59 0.02 -0.12 0
951772716 0.26392 70 0 0.07 0.26 2.15 0.04 0.43 327.69 83 2.47 79 850136348 0.9 0.98 39.75 365.38 1.12 0.21 0.15 0 noise -0.07 18.31 0.05 -0.2 0.56
951772723 14.0084 50 0 0.13 14.01 5.31 0.99 0.44 289.59 84 1.93 80 850136350 0.23 0.99 33.64 68.6 1.06 0.82 0 0 good 0.34 96.06 0 -0.21 0
951772728 2.47551 80 0 0.07 2.48 2.6 0.48 0.52 164.4 85 0.83 81 850136350 0.34 0.99 21.24 275.23 0.46 0.96 0.5 0 noise 0.21 33.52 0.02 -0.09 0.17
951772734 6.73936 50 0 0.25 6.74 7.54 1 0.41 688.85 86 4.78 82 850136348 0.51 0.99 35.23 89.33 2.58 0.15 0 0 good -0.27 126.47 0 -0.39 0
951772739 9.04798 60 0.34 0.32 9.05 7.63 1 0.48 350.1 87 4.36 83 850136352 0.41 0.99 28.07 85.58 1.12 0.26 0 0 good 0.41 110.3 0 -0.18 0
951772745 13.1074 50 -1.37 0.18 13.11 3.89 0.85 0.44 145.84 88 2 84 850136354 0.14 0.99 6.15 75.9 0.45 0.33 0.36 0.01 good 0.69 63.83 0.01 -0.1 0.24
951772751 13.2988 70 -0.27 0.07 13.3 3.09 0.86 0.45 192.6 89 2.65 85 850136354 0.24 0.99 27.96 94.12 0.66 0.3 0.13 0.01 good 0.27 57.63 0.01 -0.13 0.07
951772757 11.6707 60 -0.69 0.07 11.67 3.9 0.83 0.44 176.13 90 2.29 86 850136354 0.25 0.99 26.96 102.64 0.59 0.27 0.05 0.01 good -0.07 48.63 0.02 -0.13 0.14
951772761 13.112 50 -0.34 0.2 13.11 3.93 0.99 0.36 281.26 91 1.94 87 850136356 0.58 0.99 26.97 79.91 1.17 0.12 0 0 good -0.34 109.58 0 -0.18 0.03
951772766 16.3706 40 0 0.18 16.37 4.84 1 0.37 477.84 92 3.23 88 850136356 0.59 0.99 24.97 62.42 1.88 0.15 0 0 good -0.34 105.84 0 -0.35 0.01
951772774 0.82658 60 -0.41 0.11 0.83 2.79 0.54 0.48 218.78 93 1.5 89 850136356 0.63 0.99 29.29 396.36 0.72 0.21 0.5 0 good -0.34 29.23 0.02 -0.14 0.79
951772782 0.01033 110 -0.61 nan 0.01 3.46 nan 0.55 266.23 95 1.58 90 850136356 0.42 0.57 nan 0 0.83 0.16 0.24 0 good 1.58 31.21 0 -0.03 0
951772789 6.37034 50 -0.34 0.21 6.37 3.27 0.59 0.45 472.64 96 3.98 91 850136360 0.4 0.99 20.56 59.69 1.67 0.19 0 0.01 good -0.34 36.88 0.02 -0.22 0.17
951772795 8.44626 50 -0.34 0.11 8.45 4.18 0.87 0.38 478.23 97 4.14 92 850136360 0.41 0.99 20.14 58.02 1.86 0.15 0.02 0.01 good -0.34 68.92 0 -0.26 0.03
951772802 5.88198 50 -0.41 0.02 5.88 4.68 0.84 0.44 431.39 98 4.15 93 850136360 0.49 0.99 25.84 80.69 1.37 0.21 0 0 good 1.37 66.13 0 -0.26 0.03
951772809 7.97732 40 0 0.35 7.98 4.09 0.89 0.54 328.4 100 4.38 94 850136362 0.35 0.99 10.72 33.44 1.08 0.16 0.01 0 noise 0 61.01 0.01 -0.16 0.01
951772815 2.64416 70 -0.69 0.17 2.64 2.91 0.44 0.49 164.02 101 2.34 95 850136362 0.53 0.99 16.06 226.06 0.45 0.3 0.5 0 good -0.48 34.02 0.02 -0.09 0.19
951772822 7.36898 40 0.34 0.05 7.37 3.48 0.84 0.43 150.39 102 2.28 96 850136362 0.64 0.99 22.8 130.22 0.52 0.22 0.1 0.01 good 0.69 62.51 0 -0.11 0.05
951772829 0.13041 80 0.22 0 0.13 2.37 0 0.47 175.93 103 2.28 97 850136362 0.61 0.91 21.41 112 0.55 0.29 0.13 0 noise -0.69 18.31 0.04 -0.11 0
951772835 17.3807 50 -0.41 0.2 17.38 5.16 0.91 0.51 202.5 104 2.7 98 850136364 0.62 0.99 5.29 60.38 0.61 0.19 0.26 0.01 good nan 96.2 0 -0.1 0.17
951772842 7.26906 70 -0.27 0.04 7.27 3.17 0.73 0.43 211.27 105 2.67 99 850136364 0.79 0.99 16.03 108.38 0.73 0.19 0.5 0 good -0.41 44.39 0.02 -0.14 0.16
951772849 8.62214 50 -0.69 0.14 8.62 4.52 0.89 0.37 201.45 106 2.51 100 850136364 0.65 0.99 19.96 113.38 0.8 0.14 0.03 0 good 1.17 50.12 0.01 -0.13 0.06
951772855 1.47367 80 -0.34 -0.03 1.47 3.58 0.12 0.55 206.84 107 2.49 101 850136364 0.6 0.93 9.35 27.69 0.57 0.22 0.27 0 noise -0.21 24.61 0.03 -0.06 0.73
951772864 4.52611 50 -0.34 0.07 4.53 3.89 0.77 0.43 148.62 108 2.39 102 850136366 0.52 0.99 13.33 140.1 0.5 0.21 0.5 0 good 0 49.66 0.01 -0.09 0.08
951772870 1.61958 70 -0.41 0.06 1.62 3.81 0.49 0.43 147.3 110 2.28 103 850136366 0.5 0.99 16.89 246.2 0.52 0.18 0.5 0 good 0.07 33.54 0.02 -0.1 0.3
951772876 8.47416 70 -0.14 0.03 8.47 3.54 0.86 0.4 119.42 111 1.87 104 850136370 0.69 0.99 20.52 111.02 0.4 0.32 0.38 0 good 1.03 53.33 0.01 -0.1 0.09
951772884 12.4035 30 nan 0.16 12.4 4.15 0.97 0.4 176.36 112 2.78 105 850136370 0.55 0.99 25.42 77.54 0.61 0.22 0.04 0 good 0.34 70.3 0 -0.14 0.05
951772890 0.17412 60 3.09 nan 0.17 3.89 0.13 0.44 146.9 113 1.81 106 850136370 1.7 0.97 58.78 607.22 0.45 0.26 0.36 0 good -7.21 23.27 0.01 -0.22 2.56
951772896 1.20283 80 -0.82 -0.08 1.2 3.3 0.35 0.54 185.76 114 1.74 107 850136378 0.74 0.99 15.68 198.76 0.65 0.19 0.04 0 good -0.21 23.85 0.06 -0.1 0.7
951772900 0.94242 80 -0.14 0.05 0.94 4.59 0.68 0.59 192.54 115 2.79 108 850136370 0.3 0.99 21.51 437.7 0.61 0.12 0.5 0 good 0 43.32 0 -0.02 0.87
951772906 22.9855 50 0.34 0.09 22.99 4.6 0.98 0.38 203.78 117 3.37 109 850136370 0.59 0.99 18.9 46.22 0.73 0.26 0.01 0.01 good 1.03 83.67 0 -0.17 0.03
951772914 1.54022 20 nan 0.18 1.54 5.45 0.62 0.4 120.88 118 1.97 110 850136370 3.14 0.97 50.58 759.63 0.45 0.22 0.5 0 noise -1.51 71.52 0 -0.04 0.38
951772920 1.10528 80 -1.44 -0 1.11 5.43 0.43 0.51 134.19 119 2.25 111 850136370 2.9 0.77 42.14 249.64 0.48 0.25 0.5 0 noise 0.37 51.77 0 -0.04 1.17
951772926 9.69156 30 nan 0.18 9.69 4.84 0.86 0.4 291.26 120 3.45 112 850136372 0.45 0.99 24.01 61.88 1.11 0.15 0 0 good 0.34 57.27 0.01 -0.2 0.07
951772932 12.5661 50 -0.34 0.1 12.57 3.05 0.85 0.52 218.25 121 2.82 113 850136372 0.41 0.99 14.5 64.21 0.68 0.22 0.14 0.01 good 0.34 59.26 0.01 -0.11 0.18
951772938 8.21799 40 nan 0.15 8.22 4.21 0.88 0.38 186.65 122 2.23 114 850136372 0.52 0.99 27.14 81.32 0.68 0.22 0.02 0 good 0.76 54.89 0.01 -0.12 0.1
951772945 8.04211 60 0.07 0.12 8.04 2.78 0.88 1.37 167.01 123 1.47 115 850136376 1.92 0.99 17.94 107.7 0.12 0.78 0.21 0.01 good 0.34 60.07 0 -0.01 0.06
951772952 7.12284 50 0 0.04 7.12 2.16 0.53 0.47 183.82 124 2.21 116 850136372 0.41 0.99 27.92 155.57 0.65 0.18 0.19 0.01 good 0.34 37.44 0.04 -0.1 0.21
951772958 8.39697 40 0 0.17 8.4 4.17 0.95 0.3 191.99 125 1.94 117 850136378 0.82 0.99 30.57 122.22 0.82 0.18 0.29 0 good -0.69 70.01 0 -0.15 0.02
951772963 5.69318 80 -1.1 0.07 5.69 3.05 0.81 0.44 135.06 126 2.21 118 850136374 0.58 0.99 22.95 160.31 0.46 0.22 0.5 0 good -0.14 49.04 0.01 -0.11 0.08
951772969 15.0003 50 -0.34 0.24 15 7.38 1 0.33 383.81 127 4.02 119 850136378 0.56 0.99 31.72 52.99 1.59 0.14 0 0 good 0.34 164.76 0 -0.26 0
951772975 18.025 50 -0.69 0.15 18.03 3.12 0.98 0.18 200.75 128 2.32 120 850136378 0.3 0.99 30.23 154.39 0.77 0.1 0.07 0 good -0.07 81.73 0 -0.12 0.01
951772981 8.63671 30 0 0.16 8.64 4.18 0.77 0.36 306.99 129 3.04 121 850136378 0.62 0.99 13.54 69.85 1.19 0.15 0.02 0.01 noise 0 55.36 0.01 -0.23 0.14
951772987 9.09717 60 -1.37 0.08 9.1 3.56 0.91 0.38 247.76 130 2.69 122 850136378 0.77 0.99 23.46 117.05 0.9 0.16 0.04 0 good -0.21 60.7 0 -0.19 0.05
951772993 1.1494 70 0.82 0.02 1.15 2.47 0.51 0.4 244.41 131 2.25 123 850136378 0.75 0.99 41.19 344.67 0.87 0.19 0.02 0 good 0 25.2 0.07 -0.17 0.44
951773000 14.0709 90 -1.72 0.08 14.07 3.33 0.97 1.14 127.12 132 1.36 124 850136378 1.38 0.99 24.34 210.74 0.09 0.56 0.15 0 good -0.1 70.99 0 0 0.05
951773011 4.41874 40 0 0.02 4.42 3.83 0.36 0.37 300.06 133 2.96 125 850136378 0.58 0.99 18.27 126.76 1.14 0.16 0.02 0.01 good 0.69 36.62 0.02 -0.15 0.18
951773018 3.55971 60 0 0.15 3.56 4.48 0.84 0.45 142.74 134 2.02 126 850136380 0.15 0.98 16.14 211.63 0.51 0.3 0.5 0 good 0.41 51.89 0 -0.11 0.26
951773024 0.77678 60 0 0.05 0.78 2.43 0.19 1.25 179.59 135 1.3 127 850136376 2.27 0.82 30.33 104.36 0.05 1.77 0.32 0 good 0.27 24.9 0.04 -0.01 0.83
951773030 5.0059 50 0 0.22 5.01 5.95 0.98 0.41 371.1 136 3.12 128 850136376 0.98 0.99 31.42 76.66 1.23 0.19 0 0 good 0.14 101.31 0 -0.25 0
951773035 11.9163 70 0 0.14 11.92 4.09 0.95 1.54 150.59 137 1.38 129 850136384 6.61 0.99 17.89 122.12 0.07 nan 0.09 0 good 0.27 72.28 0 -0.02 0.06
951773043 15.1822 50 -1.03 0.18 15.18 5.08 0.96 0.48 164.73 138 2.81 130 850136386 0.59 0.99 19.82 51.72 0.49 0.25 0 0 good 1.72 90.86 0 -0.12 0.01
951773049 6.09082 70 -0.48 0.05 6.09 3.69 0.77 0.38 139.04 139 2.21 131 850136386 0.5 0.99 18.7 169.92 0.51 0.21 0.35 0.01 good 0.14 44.9 0.01 -0.09 0.13
951773054 1.77428 70 -0.34 0.06 1.77 3.25 0.53 0.43 132.96 140 1.18 132 850136378 0.98 0.99 15.27 288.64 0.42 0.16 0.5 0 good 0.07 32.68 0.03 -0.08 0.55
951773061 6.19881 70 -0.07 0.11 6.2 3.54 0.83 1.29 133.22 141 2.2 133 850136394 1 0.99 29.61 170.63 0.11 0.47 0.5 0 good 0 52.3 0.01 -0.02 0.09
951773069 11.9444 60 0 0.11 11.94 4.23 0.9 0.3 157.92 142 2.8 134 850136388 0.52 0.99 7.21 99.54 0.67 0.12 0.12 0 good 0.34 60.57 0.01 -0.15 0.43
951773075 11.032 70 -0.21 0.08 11.03 3.93 0.91 0.34 191.86 143 3.28 135 850136388 0.52 0.99 20.85 81.88 0.78 0.15 0.05 0.01 good 0.21 60.2 0.01 -0.14 0.43
951773083 15.5343 60 -0.27 0.13 15.53 4.24 0.97 0.16 156.98 144 1.95 136 850136390 0.83 0.99 17.75 160.16 0.58 0.07 0.5 0 good 0.34 76.02 0 -0.08 0.02
951773089 10.2341 50 -0.69 0.09 10.23 4.6 0.92 1.02 172.05 145 2.04 137 850136390 1.47 0.99 14.94 129.39 0.11 0.96 0.01 0 good 0.69 62.35 0.01 -0.01 0.03
951773096 19.8385 70 -0.21 0.13 19.84 5.47 0.99 0.52 139.11 146 2.21 138 850136392 0.63 0.99 26.24 76.7 0.36 0.19 0 0 good 1.03 89.03 0 -0.1 0.04
951773103 14.4526 50 0 0.22 14.45 5.06 0.99 0.32 257.15 147 4.02 139 850136392 0.46 0.99 26.96 55.8 1.15 0.12 0 0 good 0.34 92.92 0 -0.2 0
951773110 10.6374 50 0 0.09 10.64 4.11 0.95 0.38 169.87 148 2.76 140 850136394 0.83 0.99 5.46 83.69 0.64 0.16 0.5 0 good 0.34 83.03 0 -0.14 0.21
951773117 5.88622 60 0.07 0.16 5.89 3.54 0.86 0.33 202.27 149 3.09 141 850136396 0.47 0.99 39.17 108.52 0.85 0.14 0.03 0 good 0 54.03 0.01 -0.15 0.11
951773123 5.89552 90 0.16 0.09 5.9 4.78 0.92 0.69 187.26 150 3.09 142 850136396 0.58 0.99 30.77 253.26 0.45 0.12 0.5 0 good 0 73.33 0 -0.02 0.33
951773131 3.35097 60 -0.34 0.09 3.35 4.69 0.86 0.36 189.35 151 2.81 143 850136396 0.62 0.99 26.56 107.7 0.75 0.21 0.02 0 good -0.27 59.15 0 -0.17 0.41
951773137 9.55154 50 0.34 0.11 9.55 4.26 0.87 0.37 233.27 152 3.39 144 850136394 0.68 0.99 21.74 71.11 0.92 0.14 0.08 0 good 0.34 54.59 0.01 -0.18 0.06
951773144 45.8654 80 0.07 0.16 45.87 4.83 1 0.19 185.48 153 3.08 145 850136398 0.12 0.99 21.25 80.99 0.74 0.11 0.04 0 good 0.21 108.3 0 -0.06 0.01
951773151 5.87702 60 -0.14 0.03 5.88 3.81 0.82 0.49 127.27 154 1.99 146 850136398 0.37 0.99 32.52 110.64 0.43 0.21 0.13 0 good 0.34 48.69 0.01 -0.06 0.15
951773158 1.78802 100 0.12 0.06 1.79 3.37 0.57 0.44 130.19 155 1.95 147 850136400 0.18 0.87 29.06 239.81 0.48 0.21 0.5 0 good -0.14 36.38 0.02 -0.08 0.52
951773164 6.55614 70 -0.34 0.11 6.56 5.3 0.97 0.29 144.42 156 2.26 148 850136400 0.22 0.99 20.9 167.65 0.62 0.14 0.12 0 good -0.14 80.53 0 -0.1 0.07
951773171 20.5879 80 -0.07 0.17 20.59 3.85 0.98 0.19 211.29 157 2.98 149 850136402 0.14 0.99 23.52 114.04 0.82 0.1 0.5 0 good 0 91.5 0 -0.07 0.02
951773178 7.93516 40 0 0.32 7.94 7.65 1 0.38 590.54 158 5.98 150 850136402 0.52 0.99 33.4 39.36 2.15 0.22 0 0 good 0.34 175.47 0 -0.45 0
951773184 7.36464 80 -0.14 0.08 7.36 2.7 0.62 0.6 162.42 159 1.56 151 850136404 0.37 0.99 40.39 184.65 0.57 0.21 0.5 0.01 good -0.07 36.78 0.04 -0.02 0.34
951773189 5.8487 60 0 0.07 5.85 3.75 0.94 0.36 164.77 160 1.99 152 850136404 0.29 0.97 27.63 141.65 0.69 0.82 0.13 0 good -0.14 63.73 0 -0.15 0.06
951773195 12.4258 50 0.14 0.15 12.43 3.07 0.93 0.4 233.23 161 2.45 153 850136410 0.75 0.99 37 73.7 0.78 0.19 0.02 0 good -0.69 70.16 0 -0.15 0.05
951773200 7.92534 80 0 0.06 7.93 3.35 0.33 0.16 257.34 162 3.35 154 850136408 0.2 0.99 27.12 128.48 0.98 0.11 0.05 0 good -0.14 27.93 0.09 -0.15 0.91
951773205 2.09927 70 0 0.11 2.1 2.84 0.66 0.32 156.4 163 1.79 155 850136406 0.57 0.99 24.46 304.34 0.67 0.14 0.5 0 good 0.07 38.41 0.02 -0.08 0.29
951773211 24.5946 80 0 0.05 24.59 3.19 0.86 0.15 202.23 164 3.1 156 850136408 0.29 0.99 24.75 110.58 0.71 0.1 0.5 0.02 good 0.07 71.37 0.01 -0.18 0.08
951773216 8.96087 50 0 0.11 8.96 4.41 0.91 0.34 332.37 165 3.39 157 850136410 0.6 0.99 20.44 71.74 1.37 0.14 0 0 good -0.34 54.21 0.01 -0.23 0.04
951773222 2.38499 60 0 0.01 2.38 3.4 0.46 0.44 231.53 166 2.43 158 850136410 0.82 0.99 21.68 235.83 0.8 0.19 0.5 0 good -0.21 36.24 0.02 -0.15 0.63
951773227 28.6015 60 0 0.11 28.6 4.3 0.99 0.15 239.33 167 2.65 159 850136410 0.48 0.99 17.09 116.53 0.77 0.08 0.02 0 good 0.21 100.16 0 -0.16 0.01
951773233 27.4672 40 0 0.11 27.47 5.49 0.99 0.34 182.41 168 2 160 850136410 0.71 0.99 22.72 111.8 0.75 0.15 0.01 0 good 0 99.11 0 -0.11 0
951773238 21.7692 70 0 0.06 21.77 3.39 0.84 0.14 163.17 169 1.74 161 850136410 0.92 0.99 26.93 170.39 0.38 0.1 0.5 0.02 good 0 64.8 0.02 -0.08 0.07
951773242 2.26584 80 -0.21 0.1 2.27 2.96 0.34 0.34 156.46 170 2.02 162 850136412 0.27 0.99 24.2 314.85 0.65 0.16 0.5 0 good 0 30.94 0.05 -0.06 1.51
951773246 7.70462 60 -1.03 0.14 7.7 3.75 0.91 0.38 99.82 171 1.38 163 850136414 0.01 0.99 33.24 166.18 0.36 0.23 0.02 0 good -0.62 53.72 0.01 -0.05 0.03
951773251 5.49767 80 -1.99 0.08 5.5 3.07 0.9 0.41 109.77 172 1.57 164 850136414 0.08 0.99 32.51 184.18 0.41 0.21 0.5 0 good -0.21 62.22 0 -0.07 0.09
951773257 16.671 50 -0.34 0.18 16.67 9.42 1 0.37 313.63 173 5.12 165 850136416 0.45 0.99 29.81 45.37 1.22 0.18 0 0 good -0.34 185.8 0 -0.27 0
951773262 13.6102 60 -0.69 0.11 13.61 3.89 0.99 0.38 118.37 174 1.85 166 850136418 0.43 0.99 9.21 104.97 0.44 0.21 0.26 0 good -0.41 100.71 0 -0.1 0.04
951773268 5.20575 30 0 0.23 5.21 4.85 1 0.65 381.47 175 4.76 167 850136418 0.38 0.99 33.28 54.67 1.01 0.18 0 0 good -0.69 77.49 0 -0.21 0.04
951773273 7.88153 70 -0.96 0.07 7.88 3.47 0.96 0.4 128.54 176 2.18 168 850136418 0.34 0.99 24.52 126.43 0.48 0.18 0.5 0 good -0.21 72.01 0 -0.1 0.06
951773278 3.29879 80 -1.33 0.14 3.3 5.26 0.96 0.88 133.81 177 1.44 169 850136420 6.65 0.99 29.83 424.56 0.11 nan 0.5 0 good -0.34 66.03 0 -0.01 0.84
951773284 5.82824 50 -0.69 0.12 5.83 5.71 1 0.23 78.08 178 1.48 170 850136426 0.89 0.93 23.96 387.58 0.35 0.1 0.31 0 good 0 97.35 0 -0.11 0
951773289 21.2072 60 0 0.26 21.21 7.57 1 0.56 238.67 179 4.59 171 850136426 0.59 0.99 27.35 63.37 0.63 0.29 0 0 good 0.34 106.32 0 -0.11 0
951773295 0.88755 30 -0.69 0.04 0.89 5.49 0.93 0.3 145.81 180 2.35 172 850136426 4.18 0.63 31.97 430.27 0.62 0.16 0.5 0 noise 1.37 76.95 0 -0.08 0.49
951773300 17.8141 70 -1.65 0.18 17.81 5.89 1 0.6 101.59 181 2.1 173 850136428 0.7 0.99 19.36 111.53 0.23 0.23 0.14 0 good 0.89 117.76 0 -0.05 0
951773305 0.66001 110 -0.02 0.04 0.66 3.1 0.3 0.55 85.99 182 1.17 174 850136434 0.08 0.99 29.67 529.45 0.2 0.45 0.37 0 good 0.04 33.91 0.02 -0.06 0.09
951773310 0.00909 140 -0.63 nan 0.01 7.42 nan 0.48 116.77 183 2.4 175 850136436 2.4 0.48 nan 0 0.33 0.25 0.5 0 noise 0.82 116.24 0 -0.03 0
951773315 4.69124 70 -0.06 0.06 4.69 3 0.94 0.56 125.33 184 2.08 176 850136442 0.7 0.99 30.63 177.65 0.32 0.25 0.5 0 good 0.34 66.38 0 -0.05 0.14
951773320 11.3156 40 -0.69 0.21 11.32 7.86 1 0.55 294.19 185 4.98 177 850136442 0.52 0.99 30.19 58.1 0.82 0.25 0 0 good nan 118.47 0 -0.13 0
951773325 4.03867 20 -2.06 0.15 4.04 4.9 1 0.4 156.55 186 2.66 178 850136442 2.96 0.9 43.49 482.63 0.52 0.21 0.5 0 good nan 117.51 0 -0.1 0.3
951773332 3.75285 80 -1.67 0.13 3.75 3.08 0.84 1.43 83.73 187 0.45 179 850136444 1.79 0.99 30.25 288.68 0.04 nan 0.5 0 good -0.69 51.28 0.01 -0.1 0.1
951773337 10.0735 60 -0.76 0.05 10.07 5.26 0.97 1.17 183.1 188 1.15 180 850136444 3.66 0.99 30.48 87.99 0.1 nan 0 0.01 good 0.34 79.01 0 -0 0.01
951773342 11.6127 80 0.07 0.09 11.61 3.62 0.98 1.79 139.36 189 0.91 181 850136444 3.44 0.99 32.63 181.27 0.04 nan 0.27 0 good 0.48 83.64 0 -0.1 0.03
951773346 2.5774 50 -8.24 0.12 2.58 4.09 0.49 0.73 69.65 190 1.19 182 850136448 0.26 0.94 18.14 273.11 0.08 0.89 0.5 0.01 noise 2.54 51.46 0.01 -0.01 0.87
951773350 1.16966 140 1.66 0.04 1.17 nan nan 0.85 86.93 191 1.32 183 850136448 0.23 0.99 55.63 1338.52 0.08 2.1 0.5 0 noise -1.99 nan nan -0.02 8.8
951773356 2.28124 50 -6.18 0 2.28 3.49 0.51 0.67 75.9 192 1.17 184 850136448 0.22 0.98 16.7 279.14 0.13 0.74 0.5 0.01 noise 2.95 41.61 0.01 -0.03 1.99
951773361 6.95708 70 -0.21 0.1 6.96 3.09 0.86 1.52 169.74 193 1.29 185 850136450 5.68 0.99 26.49 140.71 0.09 nan 0.04 0.01 good -0.69 57.7 0.01 nan 0.04
951773368 6.06116 80 0 0.09 6.06 4.16 0.99 1.57 134.5 194 0.96 186 850136450 4.46 0.99 21.02 166.67 0.08 nan 0.5 0 good -0.16 90.78 0 -0.02 0.02
951773373 9.64351 30 nan 0.36 9.64 6.93 0.98 0.49 474.94 195 4.39 187 850136452 0.7 0.99 27.17 52.69 1.41 0.27 0 0 good 0 88.04 0 -0.19 0.03
951773378 6.23911 10 nan 0.17 6.24 4.72 0.98 0.29 226.97 196 2.16 188 850136452 0.69 0.99 14.99 272.78 0.96 0.11 0.13 0 noise nan 84.08 0 -0.11 0.03
951773384 14.4246 50 nan 0.15 14.42 2.42 0.98 1.17 157.85 198 1.6 189 850136452 1.13 0.99 16.79 124.76 0.08 0.81 0.15 0.01 good -0.34 91.76 0 -0.02 0.02
951773389 9.8353 30 nan 0.34 9.84 7.24 0.99 0.55 426.84 199 3.92 190 850136452 0.7 0.99 19.61 69.51 1.09 0.25 0 0 good 2.06 102.35 0 -0.19 0
951773395 9.01181 50 -0.93 0.06 9.01 2.96 0.91 1.24 159.3 200 1.61 191 850136452 1.09 0.99 30.83 129.41 0.05 0.78 0.04 0 good -0.34 65.39 0.01 -0.01 0.01
951773401 5.89521 40 0 0.33 5.9 7.23 1 0.55 462.34 201 5.24 192 850136454 0.59 0.99 37.99 54.37 1.44 0.18 0 0 good 0.34 115.77 0 -0.19 0
951773407 17.2197 40 -0.69 0.26 17.22 6.7 1 0.58 555.37 203 5.24 193 850136458 0.33 0.99 20.69 35.93 1.72 0.21 0 0 good -0.34 144.13 0 -0.21 0
951773412 5.74992 50 -0.34 0.08 5.75 2.99 0.66 1.33 196.12 206 1.66 194 850136460 3.53 0.99 31.43 143.77 0.09 nan 0.12 0.01 good 0.34 40.44 0.02 -0.01 0.11
951773418 7.05133 50 -0.34 0.06 7.05 3.69 0.86 1.54 181.71 207 1.53 195 850136460 8.23 0.99 22.43 105.03 0.1 nan 0.03 0 good 1.72 48.88 0.01 -0.05 0.04
951773423 9.72349 50 -0.34 0.1 9.72 4.64 0.88 1.18 295.11 208 2.39 196 850136460 1.46 0.99 12.61 60.23 0.14 1.41 0 0.01 good -0.34 59.27 0.01 -0.01 0.04
951773429 2.03365 60 -0.69 0.14 2.03 2.8 0.39 1.28 235.31 209 1.84 197 850136460 1.41 0.99 15.75 265.28 0.11 0.99 0.07 0 good 0.41 32.54 0.04 -0.01 0.09
951773435 5.71612 50 -0.69 0.03 5.72 3.53 0.8 1.14 183.96 210 1.57 198 850136460 5.01 0.99 10.59 130.1 0.1 nan 0.5 0 good 0 51.17 0.01 -0 0.08
951773441 10.7019 50 -0.34 0.19 10.7 7.37 1 0.49 522.71 212 4.61 199 850136462 0.65 0.99 32.66 93.31 1.78 0.18 0 0 good -0.69 136.86 0 -0.28 0
951773446 6.60864 60 0 0.12 6.61 2.92 0.64 1.3 183.79 213 1.67 200 850136462 1.66 0.99 20.46 146.7 0.08 0.96 0.18 0.01 good 0.82 43.43 0.02 -0.01 0.07
951773452 6.75145 40 0 0.03 6.75 2.6 0.97 0.08 168.39 214 1.59 201 850136460 322.33 0.99 31.48 529.97 -0.21 0.63 0.13 0 good 3.43 64.41 0 -0.49 0.13
951773458 8.26149 60 -0.27 0.06 8.26 3.84 0.95 0.66 254.72 215 2.7 202 850136464 0.47 0.99 26.67 81.99 0.68 0.23 0 0 good 0.34 66.96 0 -0.11 0.02
951773463 6.89054 50 0 0.22 6.89 5.76 0.96 0.52 345.3 216 4.25 203 850136466 0.5 0.99 22.9 59.85 0.96 0.25 0 0 good 1.03 59.59 0 -0.18 0.02
951773469 0.52939 60 0.55 0.05 0.53 3.4 0.28 0.54 165.48 217 2.09 204 850136466 0.67 0.99 27.75 420.22 0.43 0.3 0.18 0 good 0.34 35.02 0.01 -0.11 0
951773474 12.0999 50 -0.69 0.2 12.1 3.69 0.76 0.51 174.35 218 2.71 205 850136468 0.43 0.99 27.32 90.01 0.53 0.22 0.09 0.02 good -1.03 64.8 0.01 -0.08 0.03
951773480 8.47023 60 -1.24 0.04 8.47 3.9 0.8 0.49 174.47 219 2.62 206 850136468 0.48 0.99 15.84 83.84 0.52 0.25 0.2 0.01 good 0 48.13 0.02 -0.09 0.06
951773485 17.9799 70 0.21 0.12 17.98 4.41 0.98 0.18 149.57 220 2.31 207 850136468 0.16 0.99 19.74 206.81 0.59 0.08 0.23 0 good 0.69 75.45 0 -0.09 0.13
951773490 0.04381 130 0 nan 0.04 3.26 0 0.56 214.24 221 2.76 208 850136468 0.12 0.82 7.32 0 0.74 0.11 0.15 0 noise 0.14 14.4 0.07 -0.03 0
951773496 5.71054 80 -0.27 0.01 5.71 3.12 0.36 0.58 91.93 222 1.16 209 850136470 0.82 0.99 27.56 192.72 0.24 0.22 0.06 0.01 good -0.55 34.75 0.03 -0.03 0.06
951773501 10.275 70 0.48 0.04 10.28 2.7 0.9 0.59 135.69 223 1.75 210 850136470 0.95 0.99 26.97 154.88 0.31 0.33 0.36 0.01 good 0.69 64.96 0.01 -0.06 0.05
951773507 11.7831 50 -0.69 0.27 11.78 8.03 0.99 0.51 405.43 224 5.18 211 850136470 0.57 0.99 24.47 60.92 1.25 0.21 0 0 good -1.37 121.63 0 -0.21 0
951773513 14.1525 70 -1.92 0.15 14.15 4.16 0.99 0.66 160.14 225 2.3 212 850136472 0.44 0.99 19.17 101.51 0.34 0.27 0.02 0 good 0.27 96.26 0 -0.08 0.01
951773518 11.593 70 -0.21 0.15 11.59 4.26 0.83 0.54 161.86 226 2.55 213 850136474 0.55 0.99 18.33 103.98 0.43 0.23 0.5 0.01 good 0.21 58.78 0.01 -0.07 0.23
951773523 4.68132 70 -0.07 0.05 4.68 4.19 0.55 0.51 151.91 227 2.44 214 850136474 0.59 0.99 35.71 219.64 0.46 0.22 0.5 0 good 0.27 41.74 0.02 -0.09 0.14
951773533 7.15776 60 -0.69 0.06 7.16 4.47 0.94 0.49 151.05 228 2.43 215 850136474 0.52 0.99 12.87 123.12 0.48 0.19 0.4 0 good -0.48 64.99 0 -0.09 0.06
951773538 10.1507 50 -0.69 0.28 10.15 9.6 1 0.55 540.48 229 5.39 216 850136476 0.45 0.99 21.85 40.62 1.58 0.26 0 0 good 1.03 150.7 0 -0.29 0
951773542 4.49346 40 0.69 0.15 4.49 4.32 0.98 0.47 367.73 230 3.86 217 850136476 0.62 0.99 38.06 90.02 1.2 0.18 0 0 good 0.69 71.67 0 -0.24 0.07
951773548 0.31176 60 -0.69 nan 0.31 2.93 0.08 0.51 211.98 231 2.3 218 850136476 0.6 0.99 34.61 301.39 0.58 0.27 0.32 0 good 0.34 28.69 0.01 -0.1 0.4
951773553 8.24196 60 -1.37 0.13 8.24 3.37 0.96 0.49 168.79 232 2.07 219 850136476 0.45 0.99 25.18 131.22 0.51 0.23 0.09 0 good -0.76 78.6 0 -0.08 0.06
951773560 0.00176 160 -2.17 nan 0 4.05 nan 0.45 228.28 233 2.41 220 850136476 0.62 0.16 nan 0 0.67 0.25 0.02 0 good 1.2 1.31357e+13 nan -0.12 0
951773565 13.1914 40 -1.03 0.34 13.19 6.76 1 0.54 604.71 234 3.87 221 850136484 0.62 0.99 20.26 64.26 1.83 0.22 0 0 good 2.06 118.13 0 -0.25 0
951773570 0.0032 50 -0.34 nan 0 2.52 nan 0.52 816.2 235 2.63 222 850136484 0.94 0.26 nan 0 2.17 0.3 0.05 0 good 2.06 7.97582e+12 nan -0.59 0
951773577 8.17376 50 -0.34 0.15 8.17 2.56 0.84 1.55 220.04 236 2.19 223 850136482 1.17 0.99 16.26 119.8 0.08 0.87 0.5 0.01 good 0.69 51.93 0.01 nan 0.31
951773582 3.94536 40 0 0.07 3.95 4.42 0.92 1.19 284.5 237 2.7 224 850136482 1.59 0.99 22.8 93.8 0.17 0.74 0 0 good 0.69 54.13 0.01 -0.01 0.03
951773587 10.9628 40 -0.69 0.09 10.96 4.5 0.84 0.49 355.34 238 3.26 225 850136482 0.88 0.99 9.57 55.51 1.11 0.18 0.01 0.01 good 0.34 55.74 0.02 -0.16 0.09
951773594 10.7748 60 -1.37 0.09 10.77 2.89 0.89 1.39 195.78 239 1.84 226 850136482 1.62 0.99 26.32 87.68 0.1 0.93 0.12 0.01 good 0.07 55.24 0.01 -0.01 0.07
951773599 0.00837 40 0 nan 0.01 5.03 nan 0.22 314.04 240 2.51 227 850136482 0.54 0.38 nan 0 1.36 0.1 0.35 0 noise 1.03 45.87 0 -0.19 0
951773605 6.66568 40 -2.06 0.42 6.67 7.27 1 0.55 815.78 241 5.43 228 850136484 0.64 0.99 3.64 18.92 2.46 0.23 0 0 good 1.37 126.8 0 -0.42 0
951773611 11.5895 40 -0.69 0.19 11.59 3.61 0.99 0.54 447.84 242 2.79 229 850136484 0.76 0.99 23.75 60.14 1.36 0.22 0 0 good 0 133.46 0 -0.21 0.03
951773616 2.00193 50 -1.03 0.04 2 2 0.83 1.41 264.32 243 1.72 230 850136484 1.22 0.99 23.04 259.49 0.13 0.84 0.5 0 good -1.03 47.42 0.01 -0.04 0.28
951773622 11.3103 90 -2.27 0.17 11.31 4.64 0.99 0.49 145.35 244 1.87 231 850136486 0.05 0.99 11.37 106.8 0.49 0.26 0.01 0 good -0.27 94.97 0 -0.08 0.03
951773628 3.25208 80 -0.89 0.11 3.25 3.64 0.87 0.55 131.32 245 1.64 232 850136486 0 0.99 24.92 246.19 0.31 0.56 0.5 0 good 0.21 46.99 0.01 -0.07 0.13
951773633 1.76239 80 -0.96 0.1 1.76 4.41 0.84 0.45 136.93 246 1.83 233 850136486 0.25 0.95 26.27 377.11 0.54 0.18 0.5 0 good 0.34 45.94 0 -0.02 0.29
951773638 9.19493 50 0 0.16 9.19 6.36 0.97 0.45 249.18 247 4.24 234 850136490 0.42 0.99 31.4 68.48 0.78 0.21 0.01 0 good -0.34 75.09 0 -0.16 0.03
951773644 8.98805 50 -3.09 0.18 8.99 5.47 0.99 1.29 165.69 249 1.54 235 850136492 6.55 0.99 16.56 215.33 0.11 nan 0.02 0 good 0 81.07 0 -0.05 0.03
951773650 10.012 60 0 0.1 10.01 4.93 0.99 1.46 158.4 250 1.39 236 850136492 37.62 0.99 7.49 120.68 0.08 nan 0.5 0 good 0.21 107.54 0 -0.02 0.14
951773656 8.05689 50 0 0.23 8.06 5.52 0.98 0.48 228.31 251 3.42 237 850136494 0.21 0.99 16.32 73.49 0.72 0.3 0 0 good 0.69 89.49 0 -0.12 0.01
951773662 7.08966 50 0.69 0.1 7.09 5.17 0.97 0.48 207.4 252 3.17 238 850136494 0.21 0.99 13.48 83.55 0.65 0.3 0 0 good 0 84.78 0 -0.13 0.02
951773667 2.58474 60 -0.69 0.13 2.58 1.77 0.35 0.52 181.64 253 2.23 239 850136498 0.59 0.99 20.28 297.65 0.52 0.36 0.5 0.01 good 0.21 26.97 0.09 -0.09 0.14
951773673 11.9129 60 -0.21 0.23 11.91 5.31 0.99 0.51 340.06 254 4.1 240 850136498 0.36 0.99 20.11 58.82 1.13 0.21 0 0 good 1.03 85.8 0 -0.15 0
951773678 14.7664 50 -1.37 0.08 14.77 2.89 0.95 0.49 181.23 255 2.74 241 850136498 0.51 0.99 9.49 100.16 0.53 0.3 0.07 0.01 good 0.41 83.97 0.01 -0.1 0.05
951773683 19.4405 50 -0.69 0.09 19.44 4.64 0.95 0.52 230.66 256 2.99 242 850136498 0.59 0.99 23.33 74.55 0.68 0.37 0 0.01 good 0.41 68.55 0.02 -0.12 0.01
951773690 12.8355 50 -0.69 0.32 12.84 6.96 0.99 0.48 293.7 257 4.27 243 850136500 0.72 0.99 10.55 63.87 0.96 0.19 0 0 good 0.34 94.41 0 -0.17 0
951773696 15.4212 60 -1.03 0.2 15.42 3.34 0.99 0.52 147.07 258 2.28 244 850136500 1 0.99 11.02 151.38 0.4 0.23 0.25 0 good 0 95.7 0 -0.06 0.05
951773701 4.61828 60 0.07 0.15 4.62 2.32 0.48 0.52 126.3 259 2.47 245 850136506 0.68 0.99 13.42 211.46 0.37 0.27 0.5 0.01 good -0.34 38.91 0.05 -0.07 0.13
951773706 7.06538 50 -0.21 0.04 7.07 3.59 0.89 0.48 145.89 260 2.92 246 850136506 0.49 0.99 8.85 166.33 0.48 0.19 0.5 0.01 good 0 63.43 0.01 -0.09 0.13
951773713 10.5483 50 -0.27 0.15 10.55 2.94 0.93 0.44 100.44 261 2.74 247 850136508 0.43 0.99 6.14 136.57 0.35 0.19 0.01 0.05 good 0 131.44 0.01 -0.07 1.1
951773718 3.08065 60 0.07 0.1 3.08 2.3 0.39 1.54 99.91 262 1.05 248 850136510 5.89 0.99 17.58 278.37 0.05 nan 0.49 0 good -0.69 34.41 0.06 -0.05 0.2
951773724 0.01044 70 0.14 nan 0.01 nan nan 1.43 101.51 263 0.98 249 850136510 1.53 0.44 0 0 0.06 0.92 0.27 0 good -0.69 nan nan -0.11 0
951773730 13.4889 50 -0.34 0.09 13.49 nan nan 1.09 101.57 264 1.78 250 850136514 2.02 0.99 10.45 144.1 0.08 0.71 0.5 0 good nan nan nan -0 0.15
951773735 1.32249 170 -0.27 0.11 1.32 nan 1 0.63 41.63 265 0.29 251 850136484 3.07 0.99 34.09 770.11 0.03 0.48 0.5 nan noise 0.17 nan nan -0.02 13.29
951773741 10.9077 60 -1.37 0.13 10.91 nan 1 1.68 80.83 266 2.03 252 850136596 1.06 0.99 59.82 169.48 0.06 0.59 0.09 nan good 0.41 nan nan nan 0.04
951773747 5.22662 110 0 0.14 5.23 4.96 0.99 0.32 63.75 267 2.29 253 850136602 0.23 0.99 42.47 266.05 0.27 0.16 0.2 0.01 noise 0 109.67 0 -0.03 0.05
951773752 2.11353 140 -0.02 0.04 2.11 nan nan 1.29 38.48 268 0.61 254 850136606 0.2 0.9 100.31 816.72 0.06 0.59 0.5 nan noise -0.7 nan 0 -0.01 5.71
951773758 7.64623 110 -0.48 0.14 7.65 4.35 0.98 0.41 91.32 269 2.54 255 850136606 0.28 0.99 63.88 121.7 0.35 0.21 0 0.01 good 6.07 68.78 0.02 -0.06 0.03
951773765 1.74875 10 nan 0.04 1.75 6.96 0.99 1.37 76.16 270 1.28 256 850136608 8.53 0.99 26.93 1014.59 0.03 0.73 0.1 0 noise nan 101.25 0 -0 2.23
951773770 4.37545 90 -1.03 0.12 4.38 2.55 0.76 0.78 195.36 271 2.51 257 850136618 0.34 0.99 60.87 210.14 0.63 0.21 0.09 0.01 good 0.64 49.3 0.03 -0.06 0.73
951773775 4.7428 90 -0.34 0.09 4.74 2.79 0.9 1.14 219.62 272 2.26 258 850136618 0.64 0.99 59.76 237.24 0.24 0.38 0 0.01 good 1.45 60.3 0.01 -0.08 0.07
951773780 2.17315 100 -0.31 0.11 2.17 2.96 0.85 0.63 87.74 273 1.15 259 850136618 0.57 0.99 63.08 466.67 0.29 0.21 0.5 0 noise 0.34 46.42 0.02 -0.04 0.98
951773786 0.03276 120 -0.15 nan 0.03 3.19 0.03 0.71 153.25 275 1.18 260 850136618 0.67 0.67 7.36 12.93 0.45 0.19 0.5 0 good 0.65 24.79 0.07 -0.09 0
951773792 12.5212 120 -0.26 0.13 12.52 3.33 0.93 0.27 137.28 276 2.11 261 850136620 0.8 0.99 78.22 192.27 0.58 0.18 0.42 0.02 good 0.27 59.98 0.03 -0.12 0.13
951773797 2.61564 140 -0.22 0.04 2.62 2.05 0.36 0.95 116.94 277 1.25 262 850136620 0.76 0.99 93.15 542.37 0.41 0.22 0.46 0.01 noise -1.59 22.6 0.31 -0.03 11.48
951773803 22.0037 70 -0.48 0.07 22 3.28 0.98 0.49 94.18 278 1.57 263 850136620 0.56 0.99 68.73 155.89 0.3 0.21 0.4 0.03 good 0.34 127.75 0.01 -0.04 0.07
951773808 4.94266 80 2.75 0.16 4.94 4.1 0.87 0.67 236.02 279 3.03 264 850136620 0.48 0.99 65.47 185.28 0.77 0.32 0 0.01 good 0.55 50.89 0.03 -0.06 0
951773813 2.64488 90 4.46 0.02 2.64 3.03 0.77 0.91 146.6 280 2.12 265 850136620 0.7 0.99 60.46 290.63 0.38 0.32 0.03 0.01 good 0.77 40.81 0.04 -0.04 0.07
951773819 1.51129 90 0 0.04 1.51 2.45 0.66 0.67 264.67 281 2.88 266 850136620 0.47 0.99 47.48 1013.53 0.96 0.29 0.04 0 good 0.55 25.3 0.07 -0.1 0.47
951773824 0.10819 90 -0.41 nan 0.11 3.25 0.76 0.77 334.41 282 3.84 267 850136622 0.27 0.76 13.05 25.31 1.18 0.15 0.12 0 good 0.98 28.44 0.07 -0.09 3.31
951773832 0.97198 90 -0.62 0.19 0.97 5.86 1 0.85 280.1 283 3.76 268 850136630 0.5 0.75 44.34 126.18 0.95 0.14 0.01 0 good 1.31 76.78 0 -0.07 0.25
951773838 15.3389 80 -0.82 0.11 15.34 6.09 1 0.7 227.95 284 2.95 269 850136626 0.4 0.99 75.63 132.45 0.74 0.45 0 0 good 0.69 97.68 0 -0.09 0.04
951773843 0.53187 70 0.34 0.09 0.53 3.97 0.86 0.82 393 285 4.67 270 850136626 0.23 0.91 31.48 75.47 1.45 0.16 0 0 good 0.82 47.85 0 -0.09 4.38
951773849 2.82396 90 -1.03 0.04 2.82 2.53 0.73 0.8 132.91 286 1.95 271 850136626 0.3 0.99 49.78 224.94 0.4 0.21 0.43 0.01 noise 0.96 44.03 0.02 -0.03 0.74
951773853 0.13124 80 -0.55 nan 0.13 2.79 0.53 0.59 98.52 287 1.07 272 850136626 0.44 0.84 24.9 77.99 0.2 0.45 0.28 0 noise 1.17 35.59 0.01 -0.01 20.24
951773856 1.28798 110 -1.44 0.04 1.29 3 0.82 0.77 113.15 288 1.53 273 850136626 0.48 0.99 52.5 285.23 0.32 0.23 0.21 0 noise 0.54 39.05 0.01 -0.05 0.26
951773862 0.02532 80 -0.14 nan 0.03 2.73 0 0.7 366.57 289 2.71 274 850136626 0.33 0.34 8.96 15.9 0.81 0.19 0.2 0 noise 1.03 20.64 0.04 -0.05 0
951773869 9.21497 120 -0.07 0.1 9.22 3.15 0.98 0.22 135.98 290 1.72 275 850136634 0.48 0.99 80.15 233.28 0.61 0.15 0.5 0 good 0.16 84.98 0 -0.08 0.1
951773874 0.24201 90 0.41 -0.06 0.24 3.5 0.44 0.76 153.86 291 2.02 276 850136626 0.37 0.64 31.13 55.39 0.48 0.16 0.05 0 noise 0.82 40.93 0 -0.05 3.31
951773879 0.00424 110 0.53 nan 0 1.89 nan 0.62 281.18 292 1.73 277 850136626 0.44 0.24 nan 0 0.83 0.26 0.5 0 good 1.45 95.48 0 -0.05 0
951773886 0.02842 90 0 nan 0.03 5.69 0 0.8 659.59 293 3.31 278 850136628 0.34 0.5 11.79 0 2.27 0.16 0.03 0 good 0.63 31.39 0.01 -0.15 383.7
951773892 0.20161 110 0.41 nan 0.2 2.62 0.1 0.73 159.23 294 1.33 279 850136628 0.58 0.66 31.22 107.34 0.48 0.21 0.32 0 good 0.67 19.93 0.2 -0.04 40.97
951773897 0.03121 100 0.54 0.41 0.03 2.38 0 0.76 326.43 295 1.69 280 850136634 0.41 0.52 9.64 0 0.61 0.19 0.34 0 noise 0.76 21.08 0.08 -0.07 0
951773903 32.447 110 -0.33 0.11 32.45 5.06 1 0.26 144.45 296 2.59 281 850136636 0.39 0.99 79.63 132.54 0.65 0.16 0.03 0.02 noise 0 467.2 0 -0.12 0.03
951773908 3.27905 140 0.47 0.05 3.28 4.04 0.88 0.74 108.11 297 1.5 282 850136636 0.31 0.99 43.39 665.26 0.3 0.23 0.19 0 good 1.23 44.14 0.03 -0.03 1.87
951773914 20.7261 120 -0.54 0.17 20.73 8.21 1 0.22 325.58 298 4.36 283 850136634 0.53 0.99 84.25 143.06 1.44 0.14 0 0 good 0 147.53 0 -0.3 0
951773920 0.06861 80 0 nan 0.07 4.8 0.61 0.59 154.08 299 2.69 284 850136642 0.36 0.78 41.22 6.68 0.52 0.18 0.02 0 noise 0.48 48.62 0 -0.06 0
951773926 0.04051 100 0.12 nan 0.04 4.53 0.75 0.7 225.47 300 2.72 285 850136644 0.26 0.7 22.41 18.63 0.7 0.19 0.23 0 noise 0.96 34.24 0.01 -0.03 0
951773929 0.00279 170 0.16 nan 0 1.89 nan 0.49 100.46 301 1.63 286 850136650 0.47 0.22 nan 0 0.27 0.22 0.5 0 noise 1.06 4.034e+12 nan -0.06 0
951773931 13.1911 60 -0.14 0.05 13.19 5.7 1 1.61 185.25 302 1.42 287 850136652 3.3 0.99 78.96 135.28 0.08 nan 0 0 good -0.34 114.55 0 nan 0
951773933 26.4001 120 -0.13 0.17 26.4 5.98 1 1.85 239.93 303 1.91 288 850136652 3.05 0.99 86.1 141.9 0.23 nan 0 0 good 0 221.59 0 nan 0
951773935 15.1065 80 -0.41 0.15 15.11 7.77 1 0.45 124.1 304 3.26 289 850136658 0.42 0.99 72.62 116.5 0.43 0.19 0 0 good 0.41 231.62 0 -0.08 0
951773937 0.71911 160 0.84 0.1 0.72 1.93 0.33 0.41 104.47 305 1.49 290 850136648 0.48 0.99 27.4 417.58 0.41 0.19 0.5 0 noise 0.4 25.72 0.1 -0.04 13.33
951773940 2.06093 150 0.74 0.05 2.06 4.2 0.93 0.65 66.15 306 1.58 291 850136660 0.27 0.99 16.33 481.73 0.13 0.34 0.5 0 good 2.43 54.28 0.01 -0.01 1.62
951773943 1.61855 170 -2.52 0.05 1.62 3.22 0.71 0.49 49.55 307 0.6 292 850136668 0.89 0.99 22.75 631.52 0.15 0.3 0.5 0.01 noise 0.03 41.71 0.04 -0.01 6.45
951773945 5.53167 80 0.21 0.04 5.53 2.87 0.86 0.4 54.72 308 0.17 293 850136680 1.22 0.98 79.92 696.62 0.04 nan 0.42 0.02 noise 0.07 54.8 0.07 -0.01 2.13
951773948 11.6486 60 -0.24 0.09 11.65 3.12 0.98 1.44 72.39 309 0.56 294 850136676 3.23 0.99 38.87 110.7 0.02 nan 0.04 0.04 noise 0.69 99.72 0.01 nan 0.01
951773950 6.02014 30 -0.69 0.08 6.02 3.62 0.96 0.14 109.53 310 0.87 295 850136676 8.43 0.99 34.3 111.13 0.31 0.59 0 0 good 2.06 60.27 0.04 -0.4 0.01
951773956 2.38127 170 4.21 0.06 2.38 nan nan 1.1 38.27 311 0.52 296 850136680 5.39 0.99 63.94 1390.65 0.03 1.22 0.5 0 noise -0.06 nan nan -0.02 0.75
951773960 1.28632 170 -0.13 0.03 1.29 nan nan 2.01 39.81 312 0.47 297 850136680 3.27 0.99 53.41 1804.49 0.02 1.79 0.5 0 noise -0.05 nan nan -0.19 2.41
951773965 4.68432 80 -1.37 0.1 4.68 4.15 0.98 0.6 74.96 313 1.89 298 850136692 0.18 0.99 52.27 181.22 0.23 0.21 0 0 good 2.4 64.1 0.01 -0.03 0.02
951773969 3.59402 170 -3.85 0.02 3.59 2.46 0.81 0.03 39.51 314 0.5 299 850136680 20 0.99 34.62 810.22 0.38 nan 0.5 0.02 noise 0.3 51.72 0.04 nan 0.96
951773973 2.29695 100 -0.41 0.04 2.3 2.59 0.82 1.46 84.23 315 0.58 300 850136696 35.94 0.98 60.99 349.4 0 nan 0.5 0.01 noise -0.61 52.71 0.02 nan 1.37
951773977 2.75359 170 0.23 0.02 2.75 2.6 0.67 1.13 37.99 316 0.62 301 850136694 0.18 0.99 71.31 631.7 0.05 1.15 0.5 0.02 noise -1.01 46.87 0.05 -0.01 0.95
951773982 12.0485 80 -0.21 0.12 12.05 4.27 0.97 0.33 116.04 317 2.62 302 850136700 0.21 0.99 83.17 138.56 0.48 0.16 0 0.01 good -0.27 83 0.02 -0.06 0
951773986 8.86012 80 0.21 0.07 8.86 3.08 0.98 1.25 74.72 318 1.34 303 850136708 1.17 0.99 75.11 133.97 0.02 1.24 0 0.01 good 0.48 77.79 0.01 -0.01 0.01
951773990 2.37032 120 -1.06 0.06 2.37 2.53 0.74 0.7 93.67 319 1.59 304 850136708 0.87 0.99 35.86 422.86 0.19 0.27 0.32 0.01 good -0.29 39.73 0.08 -0.02 0.8
951773994 4.72214 140 -1.53 0.05 4.72 2.02 0.66 0.82 62.47 320 1 305 850136716 0.3 0.99 82.04 411.81 0.09 1.25 0.5 0.04 good -0.27 47.58 0.08 -0 0.83
951774002 2.18173 80 -0.82 0.05 2.18 2.83 0.73 0.63 114.76 321 1.9 306 850136716 0.14 0.99 45.77 237.25 0.29 0.41 0.09 0.02 good -0.69 35.16 0.11 -0.03 0.76
951774008 3.6709 120 -1.1 0.07 3.67 1.71 0.5 0.63 83.23 322 1.89 307 850136724 0.1 0.99 27.23 307.05 0.23 0.32 0.11 0.03 good -0.25 33.07 0.23 -0.02 0.7
951774013 4.5722 160 -0.67 0.03 4.57 1.67 0.64 0.7 58.54 323 1.1 308 850136732 0.8 0.99 81.2 447.7 0.13 0.32 0.5 0.06 noise -0.29 43.16 0.1 -0.01 1.01
951774019 3.26014 90 -0.76 0.05 3.26 1.64 0.51 0.69 108.47 324 2.06 309 850136732 0.47 0.99 53.17 300.26 0.31 0.26 0.2 0.03 good -0.69 31.61 0.18 -0.03 0.68
951774024 4.29412 70 -0.89 0.02 4.29 3.96 0.97 0.7 207.81 325 2.91 310 850136732 0.31 0.99 80.72 123.15 0.67 0.21 0 0 good 0.07 44.37 0.09 -0.04 0.03
951774030 7.90808 80 -0.55 0.01 7.91 1.53 0.8 0.7 89.88 326 1.71 311 850136732 0.44 0.99 80.38 250.49 0.25 0.19 0.08 0.08 good -0.14 55.46 0.09 -0.01 0.64
951774035 1.57298 100 -0.99 0.08 1.57 3.37 0.86 1.5 85.69 327 0.87 312 850136736 13.56 0.99 67.31 312.99 0.03 nan 0.17 0 good 0.34 46.06 0.01 nan 0.5
951774039 10.0113 110 0 0.11 10.01 3.45 0.9 0.3 161.03 328 2.88 313 850136740 0.37 0.99 71.31 159.88 0.71 0.18 0.02 0.01 good -0.2 51.8 0.04 -0.11 0.08
951774044 5.67055 120 -1.37 0.04 5.67 2.34 0.61 0.88 70.28 329 1.04 314 850136740 0.14 0.99 87.7 293.39 0.14 0.32 0.15 0.01 good -0.01 36.96 0.05 -0.02 0.8
951774049 3.17148 80 -0.89 0.24 3.17 3.81 0.93 0.82 215.25 330 3.22 315 850136740 0.19 0.99 58.81 171.21 0.67 0.22 0 0 good 0.21 48.13 0.02 -0.04 0.53
951774054 0.59067 100 -0.27 0.12 0.59 3.62 0.73 0.66 102.13 331 1.74 316 850136746 0.27 0.99 15.55 167.97 0.32 0.22 0.45 0 good -0.31 27.88 0.04 -0.01 24.76
951774059 45.3328 90 -0.48 0.11 45.33 2.86 0.93 0.23 152.21 332 2.79 317 850136748 0.42 0.99 72.59 123 0.7 0.19 0 0.06 good 0 92 0.03 -0.12 0.01
951774065 0.12969 70 -0.55 0.13 0.13 4.22 0.54 0.69 493.4 333 6.26 318 850136748 0.23 0.54 21.38 18.9 1.73 0.15 0.01 0 good 0 43.88 0 -0.15 0
951774070 4.59214 100 -0.9 0.04 4.59 2.88 0.74 0.65 120.51 334 1.77 319 850136748 0.23 0.99 51.54 251.97 0.35 0.25 0.34 0.01 good -0.07 40.79 0.04 -0.01 0.71
951774075 0.10881 80 -1.03 0.14 0.11 3.25 0.11 1.32 251.41 335 1.4 320 850136752 6.65 0.96 38.94 120.48 0.05 nan 0.19 0 good -0.14 22.44 0.04 nan 9.81
951774082 1.11096 100 -0.27 0.11 1.11 3.78 0.86 0.7 119.21 336 1.65 321 850136754 0.28 0.99 45.26 603.74 0.36 0.25 0.5 0 good -0.71 42.88 0.01 -0.02 3.77
951774086 2.80422 60 -0.34 0.1 2.8 3.77 0.94 0.89 160.07 337 2.24 322 850136762 0.05 0.99 79.82 175.54 0.47 0.22 0.01 0 good 0.55 49.99 0.01 -0.03 0.79
951774091 3.19235 70 -1.24 0.07 3.19 2.36 0.67 0.69 243.68 338 2.58 323 850136756 0.23 0.99 71.69 235.5 0.82 0.19 0.05 0 good 0.14 28.88 0.1 -0.04 0.68
951774097 22.7047 70 0 0.07 22.7 2.3 0.92 0.19 180.15 339 2.48 324 850136756 0.36 0.99 74.15 134.96 0.76 0.12 0.03 0.02 good 0.78 58.66 0.03 -0.04 0.03
951774103 1.08368 60 -0.69 0.08 1.08 5.04 0.88 0.77 356.85 340 3.01 325 850136756 0.22 0.99 52.38 97.44 1.14 0.16 0 0 good -0.14 41.28 0.01 -0.05 0.13
951774108 7.15993 70 -1.37 0.05 7.16 2.26 0.82 0.77 114.23 341 1.66 326 850136756 0.25 0.99 64.68 185.98 0.34 0.18 0.39 0.01 good 0 51 0.02 -0.02 0.41
951774113 0.09548 50 -1.37 nan 0.1 2.73 0.13 0.89 348.3 342 1.94 327 850136756 0.24 0.85 27.08 123.25 0.85 0.18 0.39 0 good 1.1 22.62 0.03 -0.06 4.25
951774118 3.24485 60 -2.06 0.01 3.24 4.3 0.89 0.88 199.59 343 1.68 328 850136756 0.25 0.92 43.88 64.34 0.7 0.25 0 0 good 0.62 52.37 0.01 -0.03 0.02
951774124 0.6009 60 -1.03 0.05 0.6 2.89 0.61 0.88 179.65 344 2.02 329 850136756 0.39 0.92 33.77 152.29 0.29 0.41 0.01 0 good 1.99 33.65 0.02 -0.02 0.64
951774130 6.34275 60 -1.37 0.02 6.34 2.02 0.33 0.23 229.95 345 3.46 330 850136756 0.41 0.99 53.39 234.85 1 0.14 0.06 0.02 good 0.07 31.67 0.11 -0.11 0.18
951774134 0.76086 60 -1.72 0.01 0.76 2.71 0.44 0.89 187.57 346 2.37 331 850136756 0.21 0.86 24.16 84.57 0.61 0.15 0.12 0 good 0 26.27 0.03 -0.03 2.07
951774140 0.20202 60 -1.72 nan 0.2 2.8 0 0.74 177.1 347 2.3 332 850136756 0.27 0.6 10.41 45.35 0.55 0.19 0.12 0 good 0.82 22.81 0.03 -0.04 5.69
951774145 0.43752 120 -0.31 0.01 0.44 3.75 0.5 0.63 81.73 348 1.18 333 850136758 0.29 0.96 51.09 540.99 0.23 0.32 0.28 0 good -0.96 32.15 0.01 -0.04 0.81
951774150 6.21327 60 0.69 -0.03 6.21 3.11 0.97 1.1 108.62 349 1.79 334 850136758 0.13 0.99 71.5 127.11 0.39 0.16 0.14 0 good 0.21 66.09 0 -0.02 0.11
951774156 0.01261 160 0.27 nan 0.01 3.47 nan 0.51 132.06 350 0.96 335 850136756 0.76 0.54 nan 0 0.34 0.27 0.5 0 good -0.14 21.37 0.01 -0.04 0
951774161 0.01891 60 -0.69 nan 0.02 5.66 nan 0.81 224.56 351 1.73 336 850136760 0.23 0.46 2.15 0 0.83 0.14 0.5 0 good 0 30.51 0 -0.02 0
951774166 6.77511 50 0 -0.04 6.78 3.16 0.9 0.85 175.1 352 2.87 337 850136760 0.24 0.99 84.7 153.21 0.56 0.15 0 0.01 good 0 51.05 0.02 -0.02 0.23
951774172 4.30187 60 0 0.08 4.3 2.18 0.69 0.85 178.52 353 2.03 338 850136760 0.32 0.99 59.94 211.89 0.37 0.16 0.03 0.01 good 0.27 39.06 0.03 -0.02 1.26
951774176 1.91233 80 -0.89 -0.01 1.91 2.58 0.77 1.02 136.69 354 2.03 339 850136760 0.41 0.99 49 275.09 0.36 0.22 0.03 0 good 1.3 50.66 0 -0.03 0.48
951774180 0.02046 70 -0.41 nan 0.02 3.6 0 0.89 194.89 355 1.4 340 850136760 0.36 0.51 3.73 0 0.66 0.18 0.5 0 good -0.96 14.7 0.02 -0.05 0
951774186 1.58507 50 -0.69 0.07 1.59 3.21 0.81 0.99 146.16 356 1.8 341 850136762 0.08 0.99 28.04 258.14 0.39 0.26 0.13 0 noise 0.34 44.04 0.01 -0.02 1.03
951774192 1.27031 60 -0.69 0.18 1.27 3.44 0.94 0.85 304.03 357 3.48 342 850136762 0.2 0.99 78.7 143.18 1.09 0.18 0 0 good 0.41 53.05 0 -0.08 0.02
951774197 14.1142 70 0 0.04 14.11 4.64 0.99 0.19 250.33 358 3.13 343 850136762 0.42 0.99 81.04 159.78 1.05 0.12 0 0 good 0.34 57.61 0.02 -0.29 0
951774203 2.40617 80 -0.21 0.04 2.41 2.16 0.49 0.69 161.55 359 1.48 344 850136764 0.65 0.99 69.53 450.92 0.49 0.16 0.5 0.01 good 0.34 31.27 0.06 -0.03 1.4
951774208 2.43108 80 -0.69 0.12 2.43 2.8 0.89 0.76 195.94 360 1.65 345 850136764 0.4 0.99 60.64 123.72 0.57 0.15 0 0 good 0.69 45.73 0.01 -0.04 0.43
951774213 8.71751 60 0.34 0.05 8.72 4.09 0.98 0.18 170.7 361 1.74 346 850136764 0.86 0.91 65.24 145.41 0.74 0.1 0 0 good 0.62 69.79 0 -0.13 0.01
951774220 2.89175 100 -0.82 -0.04 2.89 1.8 0.61 0.91 64.02 362 0.9 347 850136766 0.21 0.99 64.85 355.04 0.16 0.44 0.5 0.01 good 1.24 32.71 0.06 -0.02 1.31
951774225 3.53119 70 -0.76 0.09 3.53 5.88 0.99 0.87 194.23 363 2.85 348 850136768 0.19 0.92 60.33 77.94 0.58 0.34 0 0 good 0.14 78.44 0 -0.03 0.04
951774231 6.2483 100 0.21 0.03 6.25 3.33 0.97 0.45 76.72 364 0.97 349 850136768 0.35 0.99 86.26 203.28 0.28 0.91 0 0 good 0.53 51.92 0.02 -0.05 0.04
951774237 0.16988 50 -0.69 nan 0.17 4.66 0.47 0.8 458.59 365 3.53 350 850136770 0.74 0.89 18.23 39.95 1.62 0.12 0.01 0 good 1.03 33.88 0.01 -0.09 0
951774242 4.82031 70 -0.1 0.02 4.82 2.69 0.38 1.44 181.6 366 0.98 351 850136770 1.45 0.99 64.51 372.99 0.02 nan 0.01 0.01 good 0.69 30.51 0.04 nan 0.43
951774247 24.9531 70 0 0.05 24.95 2.67 0.94 1.85 186.73 367 1.62 352 850136770 2.23 0.99 89.09 149.85 0.13 nan 0 0.03 good 0.34 111.95 0.02 nan 0.02
951774253 4.07505 80 -0.55 0.09 4.08 3.52 0.91 1.14 118.88 368 1.08 353 850136770 16.18 0.99 65.22 274.08 0.03 nan 0.46 0 good -0.21 54.36 0.01 nan 0.2
951774258 0.63655 90 -0.62 0.01 0.64 3.45 0.74 1.32 155.92 369 1.31 354 850136770 12.57 0.94 47.63 215.11 0.04 nan 0.01 0 good 0.48 35.62 0.03 nan 2.96
951774264 4.27221 120 -0.59 -0.01 4.27 2.16 0.86 1.7 77.65 370 0.62 355 850136764 1.89 0.99 93.09 318.49 0.04 0.7 0.5 0 good 0.49 49.7 0.01 -0.03 0.41
951774269 1.69915 90 -0.27 0.04 1.7 2.53 0.52 1.29 115.55 371 1.04 356 850136774 4.9 0.99 62.05 443.7 0.03 nan 0.47 0 good 1.58 28.71 0.06 nan 2.86
951774275 3.28319 160 -0.09 0.04 3.28 2.61 0.74 1.09 66.87 372 0.63 357 850136774 5.05 0.99 80.08 340.15 0.02 nan 0.5 0.01 good 3.34 42.48 0.03 nan 0.81
951774280 0.91483 160 0.57 -0.04 0.91 1.99 0.2 0.92 116.5 373 0.7 358 850136770 4.44 0.99 75.23 803.69 0.1 1.87 0.2 0 noise 0.16 17.46 0.23 nan 40.8
951774286 7.29623 170 -0.22 0.03 7.3 2.12 0.82 1.77 28.17 374 0.27 359 850136774 1.32 0.99 58.65 506.22 0.02 nan 0.23 0.03 noise 0.11 49.62 0.04 nan 1.97
951774290 3.97678 150 0.05 0.03 3.98 2.15 0.54 1.68 66.7 375 0.61 360 850136774 3.28 0.99 77.75 408.77 0.03 nan 0.5 0.02 noise 0.49 36.58 0.08 nan 2.26
951774295 2.4254 170 0.03 0.04 2.43 2.3 0.4 1.66 61.06 376 0.4 361 850136770 1.79 0.99 39.9 314.35 0.01 nan 0.5 0.01 good 0.74 32.3 0.09 nan 2.16
951774299 0.01147 70 -0.48 nan 0.01 6.95 nan 0.76 467.28 377 3.18 362 850136770 0.74 0.38 0 0 1.5 0.11 0 0 noise 1.44 81.38 0 -0.09 0
951774304 7.5027 90 -0.96 -0.01 7.5 2.68 0.85 0.4 102.53 378 0.77 363 850136778 0.2 0.99 39.88 311.73 0.11 0.33 0.23 0.02 good 0.16 45.98 0.06 -0.03 0.6
951774308 13.8395 100 0.1 0.09 13.84 3.93 0.95 1.46 80.56 379 0.92 364 850136788 4.08 0.99 68.84 140.75 0.04 nan 0.03 0.02 good 0.41 72.65 0.03 -0 0.03
951774313 3.97595 120 0.22 0.02 3.98 1.92 0.64 1.62 77.71 380 0.57 365 850136788 2.58 0.99 40.36 342.89 0.03 nan 0.5 0.01 good 0.41 37.35 0.08 nan 1.2
951774318 4.31592 120 -0.03 0.08 4.32 2.51 0.33 0.34 101.1 381 2.24 366 850136794 0.49 0.99 32.64 267 0.4 0.23 0.12 0.02 good 0.41 31.09 0.21 -0.07 1.31
951774322 10.2349 100 -0.1 0.06 10.23 1.69 0.57 0.29 90.1 382 2.27 367 850136794 0.51 0.99 58.24 151.73 0.38 0.23 0.25 0.09 good 0.41 40.47 0.18 -0.07 0.12
951774327 5.38824 70 0 0.08 5.39 3.09 0.68 0.25 115.06 383 2.57 368 850136794 0.69 0.99 58.82 174.65 0.51 0.15 0.07 0.01 good 0.34 34.66 0.19 -0.13 0.23
951774331 6.53475 120 -0.02 0.02 6.53 1.9 0.39 0.32 79.95 384 1.88 369 850136794 0.32 0.99 50.12 195.2 0.33 0.23 0.16 0.05 good 0.34 32.66 0.25 -0.03 0.44
951774337 30.3643 60 -0.62 0.08 30.36 2.85 0.96 1.19 59.26 385 0.93 370 850136802 3.49 0.99 39.11 120.6 0.05 nan 0.18 0.2 good 0.34 187.66 0.05 -0.01 0.02
951774341 2.66141 30 -0.69 0.12 2.66 5.38 0.95 0.3 85.53 386 2.71 371 850136808 0 0.8 14.14 195.25 0.33 0.12 0.5 0 good 0.69 63.41 0 -0.03 0.09
951774347 1.14579 170 0.01 0.07 1.15 2.85 0.49 0.8 41.63 387 0.26 372 850136832 1.25 0.99 87.93 1062.08 0.03 nan 0.5 0 noise -0.08 32.54 0.1 -0 3.84
951774352 1.91512 70 0 0.16 1.92 3.33 0.93 0.69 134.32 388 3.23 373 850136828 0.29 0.99 64.79 168.91 0.39 0.21 0 0 good -0.14 42.78 0.08 -0.01 0.05
951774357 1.55748 80 -1.03 0.08 1.56 2.36 0.63 0.93 64.97 389 1.92 374 850136828 0.36 0.99 55.14 372.94 0.14 0.32 0.29 0.02 noise -0.31 41.44 0.06 -0.02 0.13
951774362 2.41196 100 0.34 -0.02 2.41 2.04 0.65 0.96 53.19 390 1.58 375 850136828 0.19 0.99 55.24 260.28 0.13 0.26 0.5 0.03 noise 1.53 44.61 0.08 -0.01 0.1
951774364 3.73487 80 -0.07 0.06 3.73 3.8 0.91 1.24 102.57 391 0.69 376 850136834 3.06 0.99 63.54 212.69 0.02 nan 0.04 0 good 0.96 59.08 0.02 nan 0.14
951774368 4.57788 80 -0.41 0.06 4.58 3.83 0.96 1.15 101.89 392 0.65 377 850136834 2.51 0.99 68.28 159.72 0.03 nan 0 0 good 0.34 54.08 0.04 nan 0.03
951774374 4.24442 100 -0.27 0.12 4.24 3.42 0.86 0.89 84.47 393 1.69 378 850136842 0.42 0.99 12.79 206.71 0.19 0.21 0.01 0.01 good 1.24 57.4 0.02 -0.02 0.43
951774380 5.31932 90 0.14 -0.01 5.32 1.5 0.7 0.82 65.51 394 1.89 379 850136836 0.26 0.99 61.32 232.11 0.17 0.26 0.49 0.06 good 0.69 48.26 0.09 -0.02 0.19
951774386 0.46253 70 -0.76 -0.01 0.46 1.87 0.51 1.46 75.94 395 0.5 380 850136832 2.19 0.99 58.01 428.43 0.02 nan 0.5 0 noise 0 31.63 0.06 nan 0.36
951774393 3.09356 110 0.21 0.03 3.09 2.25 0.73 0.29 53.02 396 0.26 381 850136834 1.38 0.99 50.4 325.33 0.18 nan 0.5 0.01 good 1.2 48.32 0.03 -0.08 0.1
951774401 2.91841 110 0.31 0.02 2.92 2.51 0.65 0.73 71.57 397 1.66 382 850136842 0.54 0.99 57.01 306.64 0.17 0.26 0.48 0.02 good 0.92 45.49 0.04 -0.01 0.19
951774407 2.73168 120 0.29 0.02 2.73 3.44 0.77 0.7 79.75 398 1.85 383 850136850 0.41 0.99 58.52 195.41 0.18 0.27 0 0.01 good 1.72 45.84 0.03 -0.03 0.11
951774414 2.32144 130 0.21 0.07 2.32 3.08 0.74 0.7 74.07 399 1.85 384 850136844 0.61 0.99 62.3 410.58 0.18 0.26 0.12 0.01 good 1.84 44.55 0.03 -0.03 0.39
951774420 4.20411 100 -0.96 0.1 4.2 3.44 0.93 0.7 65.14 400 1.67 385 850136844 0.39 0.99 59.16 256.99 0.17 0.27 0 0.01 good -0.16 57.3 0.01 -0.01 0.06
951774427 2.8065 80 -0.21 0.05 2.81 3.29 0.91 0.73 109.55 401 2.09 386 850136844 0.35 0.99 62.31 154.84 0.32 0.16 0 0.01 good 1.17 52.53 0.01 -0.03 0.03
951774433 9.01998 80 4.01 0.1 9.02 nan nan 0.04 59.68 402 0.22 387 850136848 0.67 0.99 80.03 959.77 0 nan 0.5 0 noise -0.85 nan nan -0.01 0.2
951774439 2.68983 60 0 0.13 2.69 2.61 0.83 0.67 83.93 403 1.89 388 850136850 0.16 0.99 67 154.83 0.35 0.22 0.05 0.01 good 0 41.07 0.06 -0 0.14
951774448 10.3982 120 -0.21 0.13 10.4 3.42 0.98 0.38 67.56 404 1.66 389 850136850 0.5 0.99 55.31 130.63 0.26 0.21 0.17 0.03 good 0.83 80.2 0.01 -0.06 0.03
951774454 2.77147 120 -0.1 0.07 2.77 2.46 0.82 0.44 60.56 405 1.07 390 850136852 0.5 0.99 54.28 265.16 0.2 nan 0.5 0.01 good 0.55 48.83 0.02 -0.04 0.17
951774461 1.37426 120 0.22 0.05 1.37 2.73 0.63 0.66 63.65 406 1.83 391 850136854 0.11 0.99 31.76 474.56 0.16 0.34 0.03 0.01 good 0.88 38.88 0.04 -0.02 1.33
951774466 1.02964 160 0.23 0.09 1.03 4.1 0.86 0.82 46.93 407 0.28 392 850136832 1.33 0.82 79.81 1475.42 0.07 nan 0.5 0 noise -0.46 51.38 0.01 -0.01 11.11
951774473 3.55062 70 -0.21 0.03 3.55 3.38 0.9 0.74 138.14 408 2.7 393 850136860 0.77 0.99 54.05 362.16 0.37 0.18 0.04 0 good 1.1 48.41 0.03 -0.05 0.86
951774479 3.90702 90 -0.07 0.11 3.91 4.48 0.98 0.66 107.71 409 2.43 394 850136862 0.18 0.99 56.88 176.06 0.3 0.23 0 0 good 0.96 67.32 0 -0.06 0.03
951774484 2.11404 160 -0.35 0.08 2.11 2.46 0.69 0.26 62.43 410 1.28 395 850136862 0.22 0.99 38.45 489.11 0.29 0.27 0.5 0 noise 0.14 41.47 0.04 -0.04 0.97
951774491 1.71424 170 -0.01 -0.02 1.71 2.66 0.79 0.78 57.17 411 1.3 396 850136862 0.02 0.99 43.63 531.54 0.13 0.38 0.5 0 good 1.59 46.1 0.02 -0.02 0.28
951774502 6.93642 100 -0.48 0.09 6.94 2.94 0.9 0.23 87.44 412 2.1 397 850136868 0.57 0.99 47.8 171.28 0.32 0.14 0.06 0.01 noise 0.14 57.13 0.02 -0.09 0.13
951774507 2.62225 120 -1.24 0.09 2.62 3.22 0.95 1.36 74.85 413 1.72 398 850136860 1.23 0.99 45.1 263.59 0.03 1.79 0.45 0.01 good 0.32 75.28 0 -0 0.07
951774513 0.66073 120 -0.14 0.08 0.66 2.51 0.44 0.7 65.77 414 1.92 399 850136868 0.4 0.99 28.41 308.3 0.19 0.23 0.17 0 noise 1.77 34.62 0.04 -0.02 1.24
951774520 17.2249 100 -0.21 0.05 17.23 3.1 0.96 0.26 87.51 415 2.06 400 850136870 0.15 0.99 55.98 102.19 0.4 0.26 0 0.03 good 0.47 85.53 0.03 -0.09 0.02
951774527 0.80592 80 -0.21 0.11 0.81 2.48 0.96 0.67 114.4 416 2.47 401 850136870 0.06 0.98 66.14 80.9 0.38 0.18 0 0 good 0.76 51.83 0 -0.05 0.06
951774533 0.02645 80 -0.27 nan 0.03 4.01 0.22 0.63 92.99 417 1.11 402 850136866 0.14 0.41 14.12 4.93 0.26 0.26 0.33 0 good 1.03 43.48 0 -0.04 0
951774538 0.09207 50 -1.03 0.19 0.09 4.47 0.57 0.7 184.48 418 1.85 403 850136872 0.86 0.64 46.04 71.1 0.57 0.18 0.03 0 noise -0.69 57.93 0 -0.03 0
951774544 0.11501 60 -0.82 nan 0.12 3.87 0.44 0.74 165.07 419 1.6 404 850136872 0.71 0.91 53.04 41.91 0.51 0.21 0.04 0 noise -0.34 35.44 0.01 -0.04 0
951774549 1.59003 120 0.34 0.07 1.59 2.9 0.65 1.32 69.02 420 0.66 405 850136872 4.74 0.99 68.88 410.76 0.02 nan 0.5 0.01 good 1.17 39.87 0.03 nan 0.34
951774555 0.01447 60 0.07 nan 0.01 8.49 0 0.66 199.15 421 3.31 406 850136874 0.12 0.28 0.89 0.55 0.56 0.3 0 0 good 0.34 70.19 0 -0.08 0
951774562 2.70048 90 0.48 -0.02 2.7 3.81 0.91 0.59 85.33 422 1.06 407 850136876 0.27 0.99 63.44 164.29 0.21 0.98 0.12 0.01 good 0.14 65.67 0.01 -0.04 0.06
951774567 2.73571 70 0.62 0.06 2.74 5.91 0.99 0.67 196.75 423 3.05 408 850136882 0.5 0.99 52.12 119.03 0.58 0.18 0 0 good 0.55 76.63 0 -0.06 0.04
951774572 2.62421 110 0.14 0.06 2.62 2.64 0.64 0.65 133.43 424 2.1 409 850136880 0.11 0.99 67.39 266.79 0.39 0.25 0.22 0 good 0.73 37.36 0.05 -0.04 0.45
951774576 3.32142 130 -0.51 0.07 3.32 3.54 0.8 0.27 107.74 425 1.84 410 850136880 0.03 0.99 55.99 364.22 0.47 0.22 0.5 0 good 0.04 48.48 0.02 -0.07 0.3
951774582 1.86366 100 0.33 0.03 1.86 2.76 0.61 0.65 90.22 426 1.7 411 850136882 0.85 0.99 52.68 338.21 0.24 0.19 0.43 0 good 0.76 33.37 0.06 -0.04 0.47
951774588 10.9189 90 0.27 0.17 10.92 2.88 0.79 0.59 151.18 427 2.84 412 850136884 0.24 0.99 52.38 127.28 0.41 0.32 0.03 0.02 good 0.41 44.4 0.09 -0.07 0.17
951774592 18.9308 90 -0.55 0.07 18.93 3.12 0.9 0.34 94.99 428 1.48 413 850136880 0.05 0.99 59.9 138.9 0.34 0.3 0.13 0.03 good 0.27 70.07 0.03 -0.07 0.06
951774598 3.77403 80 0.21 0.02 3.77 2.01 0.36 0.66 112.04 429 1.68 414 850136884 0.07 0.93 45.85 163.11 0.25 0.29 0.07 0.01 noise 0.41 30.26 0.09 -0.04 0.55
951774603 5.37553 80 0.34 0.03 5.38 2 0.59 0.49 114.45 430 2.27 415 850136884 0.06 0.99 31.15 234.55 0.48 0.21 0.5 0.02 good 0.48 40.27 0.07 -0.04 0.14
951774609 1.08079 100 0.07 0.11 1.08 2.37 0.16 0.38 125.05 431 1.8 416 850136884 0.03 0.93 26.05 125.08 0.37 0.27 0.5 0 good 0.1 25.83 0.1 -0.02 1.56
951774614 9.83375 110 0.96 0.1 9.83 2.95 0.89 1.4 69.95 432 0.97 417 850136886 9.51 0.99 51.27 203.8 0.02 nan 0.36 0.01 good 1.23 56.93 0.01 nan 0.02
951774620 8.5343 80 -1.24 0.08 8.53 4.09 0.95 0.8 89.47 433 1.83 418 850136888 0.29 0.99 47.76 121.7 0.24 0.23 0.01 0 good -0.41 56.48 0.01 -0.03 0.04
951774625 2.47717 90 -0.1 0.07 2.48 3.29 0.5 1.48 102.21 434 0.69 419 850136890 2.14 0.99 40.7 294.74 0.02 nan 0.5 0 good 0.89 35.11 0.03 nan 0.37
951774631 8.54856 150 0.61 0.09 8.55 2.01 0.71 0.58 97.21 435 1.87 420 850136892 0.3 0.99 61.2 191.53 0.22 0.36 0.11 0.02 good 1.04 42.67 0.05 -0.04 0.08
951774636 17.9195 70 0.27 0.08 17.92 3.02 0.83 0.59 130.61 436 2.47 421 850136892 0.34 0.99 53.63 134.68 0.32 0.3 0.05 0.04 good 0.34 61.25 0.02 -0.06 0.22
951774641 0.00083 170 -0.25 nan 0 2.91 nan 0.49 234.29 437 3.46 422 850136884 0.65 0.07 nan 0 0.61 0.23 0.03 0 good -0.25 1.12985e+12 nan -0.25 0
951774648 13.007 60 0.41 0.11 13.01 2.89 0.81 0.62 138.38 438 2.5 423 850136898 0.37 0.99 60.97 163.54 0.33 0.21 0.25 0.02 good 1.37 56.87 0.03 -0.09 0.24
951774653 11.9066 70 -0.69 0.2 11.91 4.64 0.94 1.43 265.57 439 1.72 424 850136906 1.78 0.99 50.63 123.41 0.12 1.77 0 0.01 good 0.69 65.81 0.01 -0.07 0
951774659 7.84381 130 0.43 0.18 7.84 5.11 0.97 0.62 164.29 440 3.54 425 850136900 0.47 0.99 56.89 137.39 0.44 0.22 0 0 good 0.88 58.94 0.01 -0.07 0.03
951774664 9.02308 140 0.2 0.08 9.02 2.62 0.73 0.62 132.11 441 2.94 426 850136900 0.54 0.99 71.37 203.56 0.33 0.25 0 0.02 good 0.66 40.85 0.06 -0.06 0.18
951774670 2.4595 100 -0.27 0.09 2.46 2.86 0.64 0.66 82.36 442 1.83 427 850136900 0.37 0.99 29.42 306.66 0.22 0.22 0.07 0 good 1.22 43.15 0.01 -0.01 0.13
951774676 8.36369 80 0.61 0.03 8.36 2.8 0.69 1.44 163.71 443 1.05 428 850136906 5.69 0.99 48.81 171.81 0.06 nan 0.03 0.01 good 0.76 43.67 0.05 -0.04 0.07
951774682 3.01792 60 -1.37 0.1 3.02 2.85 0.81 1.44 147.62 444 1.04 429 850136906 22.51 0.99 58.9 214.54 0.05 nan 0.01 0 good 0.34 42.41 0.02 -0.06 0.1
951774686 2.36773 80 -2.75 0.06 2.37 2.14 0.41 1.41 109.17 445 0.73 430 850136906 3.57 0.99 36.36 362.86 0.03 nan 0.14 0 good 0.74 39.55 0.02 -0 0.49
951774692 5.19159 110 0.12 0.07 5.19 2.3 0.79 1.15 94.05 446 1.77 431 850136908 1.35 0.99 44.77 254.03 0.04 1.07 0.39 0.01 good 0.88 49.76 0.02 -0 0.16
951774697 3.62357 60 0 0.05 3.62 3.15 0.71 1.73 117.94 447 2.14 432 850136908 1.05 0.99 55.54 249.49 0.08 0.6 0.41 0 good 0.34 50.31 0.01 nan 0.08
951774704 2.26626 120 0.56 0.06 2.27 2.65 0.82 1.24 74.66 448 0.52 433 850136906 2.1 0.99 30.59 265.47 0.02 nan 0.28 0 good 0.96 52.52 0.01 nan 0.14
951774708 2.1035 140 -0.08 0.09 2.1 2.94 0.42 1.65 79.6 449 0.49 434 850136906 2.12 0.99 33.55 366.77 0.05 nan 0.5 0.01 good 0.35 34.32 0.04 nan 0.91
951774713 3.15867 60 nan 0.08 3.16 3.74 0.95 1.41 193.99 450 0.91 435 850136906 63.14 0.99 50.63 163.32 0.03 nan 0 0 good 0.51 43.98 0.02 -0.06 0
951774719 2.25675 50 1.37 0.11 2.26 4.41 0.99 1.28 110.42 451 2.23 436 850136908 1.07 0.99 47.74 162.64 0.05 1.15 0 0 good 0.69 60.58 0 -0.02 0
951774724 4.8387 170 0.61 0.05 4.84 1.74 0.47 1.37 80.74 452 0.3 437 850136906 1.49 0.99 41.76 467.98 0.02 nan 0.14 0.01 noise 1.09 36.72 0.06 nan 0.2
951774730 15.427 80 -1.37 0.04 15.43 3.51 0.97 1.7 69.62 453 1.56 438 850136912 1.1 0.99 39.85 141.09 0.05 0.59 0.05 0.01 good 0.18 77.61 0.01 nan 0.01
951774736 8.75523 70 -0.34 0.07 8.76 3.87 0.98 0.69 178.88 454 3.54 439 850136914 0.4 0.99 52.78 112.72 0.51 0.19 0 0.01 good 0.82 73.85 0 -0.05 0.01
951774741 1.59148 90 -0.34 0.16 1.59 3.04 0.83 0.76 166.98 455 2.94 440 850136914 0.44 0.99 49.46 151.12 0.48 0.19 0 0 good 0.91 40.04 0.02 -0.03 0.09
951774745 4.33163 70 -0.62 0.06 4.33 3.61 0.82 0.47 95.45 456 1.86 441 850136916 0.41 0.99 54.87 198.66 0.19 0.27 0.28 0.02 good 1.03 49.17 0.02 -0.02 0.25
951774752 7.80909 110 0.14 0.05 7.81 2.59 0.86 0.29 67.64 457 1.23 442 850136922 0.03 0.94 32.6 232.88 0.31 0.76 0.23 0.02 good -0.2 55.77 0.04 -0.1 0.11
951774757 1.71279 70 0.34 0.11 1.71 4.07 0.83 0.56 108.2 458 1.87 443 850136916 0.28 0.99 39.21 243.32 0.26 0.19 0 0 good 0.62 50.36 0.01 -0.04 0.15
951774761 2.3604 130 2.27 0.02 2.36 2.28 0.22 1.63 67.78 459 1.18 444 850136914 1.43 0.99 30.06 479.03 0.05 0.71 0.5 0.02 good -0.3 33.12 0.07 nan 0.34
951774768 3.21633 120 -0.34 0.02 3.22 2.16 0.53 1.63 72.82 460 1.24 445 850136914 1.13 0.99 39.56 358.59 0.04 0.55 0.5 0.02 good 0.73 41.79 0.04 -0.03 0.17
951774772 1.79246 110 -0.55 0.1 1.79 2.42 0.76 0.74 100.48 461 1.84 446 850136922 0.08 0.99 39.26 403.82 0.26 0.36 0.31 0 good 1.01 42.84 0.02 -0.03 0.48
951774777 5.85552 90 0.34 0.05 5.86 3.03 0.66 0.3 82.41 462 1.31 447 850136922 0.11 0.83 34.03 151.07 0.31 0.23 0.01 0.05 good 1.01 53.74 0.04 -0.08 0.15
951774783 1.22463 90 0.34 0.1 1.22 2.7 0.7 0.69 98.82 463 1.47 448 850136922 0.12 0.99 51.74 254.07 0.23 0.33 0.02 0 good 1.37 35.65 0.06 -0.02 0.75
951774785 3.60363 130 0.14 0.01 3.6 2.68 0.43 0.38 95.79 464 1.47 449 850136922 0.1 0.89 46.8 239.8 0.33 0.56 0.02 0.03 good 0.85 38.17 0.08 -0.06 0.27
951774791 3.0265 170 0.73 -0 3.03 1.81 0.35 0.82 51.49 465 0.96 450 850136926 0.24 0.99 63 504.75 0.1 0.63 0.5 0.02 noise 1 33.07 0.1 -0.02 0.43
951774796 2.2892 120 0.24 0.04 2.29 2.75 0.73 0.36 69.4 466 1.35 451 850136928 0.32 0.99 54.52 431.21 0.26 0.19 0.5 0.01 good 0.76 44.19 0.04 -0.05 0.67
951774800 1.44009 170 1.18 0.01 1.44 1.61 0.32 1.17 56.62 467 1.1 452 850136926 0.08 0.99 30.19 1051.97 0.08 1.04 0.5 0.01 noise 0.27 32.56 0.07 -0.06 1.49
951774806 3.8847 60 -1.03 0.06 3.88 4.1 0.97 0.44 74.27 468 1.45 453 850136928 0.15 0.92 26.31 255.6 0.2 0.32 0.28 0.01 good 0 60.1 0.01 -0.02 0.34
951774812 0.85417 110 0.22 0 0.85 2.63 0.42 1.46 68.2 469 0.97 454 850136930 8.99 0.97 31.66 325.81 0.03 nan 0.5 0 good 0.82 33.21 0.07 nan 1.43
951774817 1.44153 130 1.38 0.09 1.44 3.1 0.82 0.71 84.16 470 1.79 455 850136940 0.75 0.99 50.6 455.9 0.22 0.22 0.28 0.01 good 0.82 39.57 0.08 -0.03 0.63
951774823 0.06531 60 -0.21 nan 0.07 6.11 0.62 0.66 175.77 471 3.74 456 850136932 0.03 0.76 9.54 19.61 0.62 0.15 0.06 0 noise 1.03 46.62 0 -0.06 9.08
951774827 0.51503 110 0.35 0.17 0.52 4.36 0.92 1.02 135.89 472 1.76 457 850136938 1.96 0.98 38.82 139.4 0.07 nan 0.01 0 good 1.06 38.97 0.05 -0 0.58
951774832 0.86151 100 -1.58 nan 0.86 3.57 0.84 0.56 85.1 473 1.6 458 850136936 0.41 0.99 29.97 420.56 0.19 0.25 0.16 0.01 good -0.27 44.59 0.03 -0.02 1.41
951774838 0.71219 150 0.65 -0 0.71 1.98 0.24 1.55 78.18 474 1.11 459 850136938 9.16 0.99 24.26 348.76 0.02 nan 0.5 0.01 good 0.81 28.65 0.13 nan 4.05
951774845 5.84715 120 -0.76 0.11 5.85 4.77 0.99 1.83 91.16 475 2.08 460 850136942 1.15 0.99 43.93 260.14 0.09 0.4 0.01 0 good -0.45 67.25 0.02 nan 0.24
951774850 1.69874 70 0.21 -0.07 1.7 4.34 0.96 0.73 158.68 476 2.82 461 850136946 0.39 0.99 45.51 274.25 0.44 0.19 0.01 0.01 good 0.69 58.83 0.01 -0.07 0.72
951774856 3.67338 150 1.04 0.08 3.67 1.71 0.6 1.09 38.39 477 0.5 462 850136938 2.39 0.99 29.29 555.67 0.01 nan 0.5 0.1 noise 1.4 44.9 0.1 nan 0.54
951774862 2.26429 170 2.63 0.11 2.26 nan nan 1.02 45.11 478 0.55 463 850136938 2.25 0.99 99.41 2293.56 0.04 1.4 0.5 0 noise 0.13 nan nan -0.02 0.43
951774866 2.56294 170 1.12 0.01 2.56 1.38 0.42 1.22 44.94 479 0.91 464 850136946 0.67 0.99 28.87 791.8 0.02 0.87 0.5 0.06 noise 0.92 39.7 0.11 -0.05 0.35
951774872 3.04841 70 -0.34 0.08 3.05 2.45 0.81 1.52 64.25 480 0.56 465 850136952 3.8 0.99 45.33 298.42 0.03 nan 0.43 0.06 good 0 46.05 0.25 nan 0.58
951774878 3.83149 100 0.82 0.09 3.83 2.36 0.83 0.73 53.01 481 1.63 466 850136956 0.32 0.99 16.38 275.97 0.13 0.36 0.5 0.08 good 1.37 56.04 0.08 -0.01 0.21
951774884 0.12938 30 0.34 nan 0.13 3.83 0.75 0.96 172.78 482 3.6 467 850136962 0.51 0.89 18.16 17.54 0.51 0.15 0.15 0 good nan 47.65 0.01 -0.07 2.31
951774890 0.00176 130 -2.14 nan 0 nan 1 1.73 107.35 483 0.72 468 850136988 1.4 0.12 nan 0 0.11 0.38 0.5 nan noise -2.2 nan nan nan 12550.6
951774895 8.19463 110 0.25 0.12 8.19 1.48 0.92 0.76 32.22 484 0.72 469 850136998 0.37 0.99 78.41 707.35 0.03 1.13 0.5 0.57 noise 0.34 409.03 0.25 -0.01 2.43
951774900 2.1871 90 0.07 0.04 2.19 1.43 0.28 0.52 45.42 485 0.81 470 850137006 0.16 0.58 22.2 159.99 0.09 0.62 0.26 0.08 noise nan 20.35 0.44 -0.04 9.84
951774906 0.01126 120 -0.03 nan 0.01 0.94 0 0.47 54.53 486 0.63 471 850136992 0.53 0.41 0 0 0.14 nan 0.5 0 noise 0.27 9.31 0.28 -0.06 1221.15
951774913 2.63393 120 0.22 0.04 2.63 3.4 0.9 1.04 39.42 487 0.55 472 850136992 0.6 0.9 72.13 521.61 0.01 nan 0.5 0.01 noise 0.07 53.63 0.03 -0.01 3.27
951774918 0.81625 100 0.17 0.24 0.82 2.89 0.72 0.63 94.39 488 2.09 473 850137002 0.9 0.97 18.75 284.11 0.11 0.47 0 0.02 noise 0 22.73 0.23 -0.08 13.25
951774924 0.00496 80 nan nan 0 3.07 nan 0.76 76.77 489 1.99 474 850136298 1.61 0.31 nan 0 0.15 0.67 0.34 0 good -1.57 9.88 0 -0.03 0
951774930 8.73084 70 -0.06 0.04 8.73 2.64 0.89 0.44 142.87 490 1.75 475 850136330 0.34 0.99 31.58 132.58 0.48 0.25 0.2 0 good 0.69 57.48 0.01 -0.06 0.04
951774934 21.6061 70 0 0.04 21.61 4.61 0.94 0.18 241.83 491 3.45 476 850136340 0.28 0.99 28.93 86.06 0.92 0.1 0.01 0.01 good 0.48 104.75 0 -0.23 0.03
951774941 0.55357 50 0.34 -0.08 0.55 4.62 0.65 0.38 186.16 492 2.85 477 850136370 0.93 0.96 81.98 2071.39 0.65 0.25 0.12 0 good 1.03 44.9 0 -0.27 1.64
951774947 6.24169 60 -0.34 0.02 6.24 4.39 0.99 0.48 124.56 493 1.68 478 850136430 0.67 0.99 17.09 137.53 0.19 0.27 0.48 0 good 0.41 98.15 0 -0.04 0.03
951774952 10.4657 60 0.82 -0.01 10.47 2.94 0.88 0.55 193.46 494 2.5 479 850136466 0.59 0.99 21.77 83.73 0.5 0.29 0.16 0.01 good 0.34 63.47 0.01 -0.13 0.06
951774958 9.37008 70 -1.44 0.13 9.37 3.65 0.98 0.54 211.18 495 2.41 480 850136476 0.54 0.99 31.66 119.51 0.6 0.27 0.01 0 good -0.69 81.18 0 -0.12 0.04
951774963 3.82084 50 -0.41 0.06 3.82 3.51 0.74 0.44 142.49 496 3.63 481 850136508 0.53 0.99 5.25 112.43 0.47 0.25 0 0.01 good 0 41.84 0.08 -0.1 0.04
951774969 0.28262 40 0 -0.02 0.28 2.47 0.11 0.43 108.18 497 1.23 482 850136510 0.57 0.98 19.31 75.06 0.4 0.16 0.01 0 good 0 28.9 0.08 -0.05 0
951774975 0.0279 90 0.34 nan 0.03 4.51 0.22 0.67 606.55 498 4.81 483 850136618 0.33 0.26 25.24 23.69 2.3 0.14 0 0 good 0.83 33.99 0.01 -0.3 0
951774982 0.05735 90 -0.55 nan 0.06 5.22 0.43 0.62 213.86 499 2.29 484 850136618 0.4 0.38 17.72 14.68 0.72 0.19 0.06 0 good 0.76 29 0.01 -0.04 23.55
951774988 0.00372 100 0.41 nan 0 4.95 nan 0.7 587.48 500 4.95 485 850136622 0.27 0.23 nan 0 1.92 0.14 0.01 0 good 0.83 8.57703e+11 nan -0.16 0
951774995 0.30174 90 0.07 nan 0.3 5.49 0.85 0.85 315.86 501 2.9 486 850136628 0.37 0.93 32.79 73.86 1.1 0.15 0 0 good 1.1 41.97 0.01 -0.06 10.21
951775003 0.02325 100 0 nan 0.02 3.69 0 0.71 408.64 502 2.83 487 850136628 0.41 0.68 0 0 1.45 0.15 0.07 0 good 0.81 18.33 0.18 -0.04 0
951775009 0.07079 70 -0.48 nan 0.07 6.1 0.6 0.76 632.5 503 4.76 488 850136770 0.54 0.7 5.73 2.59 2.23 0.16 0 0 good 1.37 39.04 0 -0.1 0
951775014 0.07823 90 -0.29 nan 0.08 4.14 0.22 0.76 321.04 504 2.78 489 850136778 0.26 0.84 35.95 17.8 0.83 0.21 0.04 0 good 1.37 19.27 0.18 -0.07 25.32
951775020 0.50676 90 -0.41 0.09 0.51 3.53 0.46 1.19 117.58 505 0.74 490 850136834 2.73 0.99 19.11 256.57 0.02 nan 0 0 good 0.37 35.39 0.02 -0.01 0.15
951775028 0.01891 70 -0.34 nan 0.02 2.87 0 0.6 226.55 506 4.24 491 850136870 0.26 0.43 0 0 0.73 0.19 0 0 good 0.48 44.86 0 -0.08 0
951775033 0.43236 70 0 0.08 0.43 2.77 0.78 0.67 117.32 507 0.51 492 850136866 0.54 0.99 50.93 264.25 0.18 nan 0.08 0 good 0.76 41.14 0.01 -0.02 0.83
951775039 0.07451 100 -0.41 nan 0.07 6.13 0.78 0.65 136.88 508 1.25 493 850136866 0.27 0.84 28.4 10.41 0.44 0.81 0 0 good 2.01 60.3 0 -0.11 0
951775044 0.03813 90 -0.34 nan 0.04 5.05 0.13 0.66 99.64 509 0.73 494 850136866 0.54 0.74 26.54 2.47 0.18 nan 0.12 0 good 1.15 40.78 0 -0.04 0
951775051 0.21969 50 0.69 0.17 0.22 6.27 0.95 0.62 320.19 510 4.7 495 850136874 0.01 0.8 6.13 36.68 1.01 0.23 0 0 good 1.37 61.98 0 -0.14 0.8
951775057 0.85789 80 -0.06 0.09 0.86 4.09 0.75 0.62 160.11 511 3.58 496 850136900 0.46 0.99 26.26 264.5 0.51 0.21 0 0 good 1.03 42.05 0.01 -0.06 0.11
951775065 2.42664 80 0.69 -0.07 2.43 4.11 0.93 0.59 73.88 512 1.58 497 850136924 0.11 0.99 50.32 220.53 0.18 0.27 0.06 0.01 good 0.69 59.05 0.01 -0.02 0.2
951775073 0.41376 40 -0.62 0.1 0.41 4.39 0.89 0.93 113.82 513 2.72 498 850136962 0.61 0.94 35.05 129.47 0.33 0.15 0.01 0.01 good nan 58.53 0.01 -0.02 0.68
951775080 0.1362 100 0.25 nan 0.14 3.29 0.78 1.13 176.5 514 2.51 499 850137002 1.03 0.91 9.99 27.06 0.18 0.45 0.02 0 noise 0 14.93 0.4 -0 100.22
951775086 0.01912 90 -0.27 nan 0.02 4.46 0 0.76 515.17 515 3.77 500 850136628 0.35 0.43 4.77 0 1.67 0.16 0 0 good 0.82 31.88 0.01 -0.13 0
951775092 0.03048 80 0.24 nan 0.03 5.06 0 0.66 105.24 516 0.46 501 850136874 0.5 0.51 3.4 3.18 0.09 1.44 0.14 0 good 1.03 48.26 0 -0.02 0
951775099 0.01653 50 -1.72 nan 0.02 3.24 nan 0.58 1043.54 517 4.21 502 850136484 0.75 0.64 nan 0 2.64 0.26 0.31 0 good 1.03 34.93 0 -0.6 0
951775105 0.0124 50 -1.03 nan 0.01 2.97 nan 0.58 899.7 518 2.96 503 850136484 0.86 0.61 nan 0 1.99 0.3 0.23 0 good 1.03 43.76 0 -0.58 0
951775110 0.02656 50 -0.34 nan 0.03 7.23 0 0.87 501.68 519 4.43 504 850136760 0.21 0.55 7.89 8.01 1.68 0.12 0.02 0 good 1.03 45.78 0 -0.11 54.92
951775116 0.26196 130 0 0.08 0.26 3.86 0.4 0.63 123.49 520 2.81 505 850136850 0.42 0.98 46.99 132.58 0.36 0.21 0 0 good 1.82 35.12 0.02 -0.05 0
951775173 5.91525 80 nan nan 5.92 3.05 0.87 0.59 19.57 0 2.63 0 850139164 0.6 0.99 19.36 322.9 0.22 0.37 0.4 0.01 good 2.8 36.91 0.01 -0.05 0.18
951775180 7.71454 60 nan 0.05 7.72 3.49 0.93 0.58 28.79 1 3.19 1 850139164 0.37 0.99 24.75 260.29 0.29 0.23 0.44 0.01 good -0.08 51.71 0.01 -0.04 0.1
951775184 3.89483 40 nan 0.05 3.9 2.4 0.65 0.63 85.46 2 1.83 2 850139168 0.51 0.99 29.54 445.13 0.18 0.48 0.5 0.01 good 0.48 21.3 0.04 -0.04 0.11
951775192 9.07888 40 nan 0.15 9.08 3.69 0.97 0.54 62.06 3 4.93 3 850139164 0.49 0.99 22.09 72.76 0.61 0.25 0 0 good 0.34 47.27 0 -0.09 0.01
951775198 3.91622 30 nan 0.07 3.92 2.62 0.84 0.58 140.92 4 2.68 4 850139168 0.41 0.99 20.91 225.66 0.42 0.29 0.08 0 good 0.34 23.85 0.04 -0.05 0.15
951775206 8.11248 50 nan 0.13 8.11 3.83 0.92 0.59 120.14 5 2.59 5 850139168 0.33 0.99 16.89 293.59 0.35 0.23 0.01 0.01 good -0.41 58.18 0.01 -0.06 0.1
951775212 2.37393 40 nan 0.11 2.37 3.66 0.86 0.56 96.97 6 1.66 6 850139170 0.42 0.99 23.08 456.89 0.31 1.02 0.26 0 good 0 37 0 -0.05 0.06
951775218 8.28102 40 nan 0.27 8.28 7.96 1 0.59 234.4 7 3.16 7 850139170 0.04 0.99 26.83 66.33 0.66 0.37 0 0 good 0.69 138.62 0 -0.1 0
951775223 7.29561 40 -2.06 0.29 7.3 3.49 0.98 0.6 258.57 8 4.48 8 850139172 0.49 0.99 27.91 83.16 0.74 0.26 0 0 good 0.69 59.62 0 -0.11 0
951775230 5.32149 50 -0.69 0.15 5.32 2.52 0.97 0.59 139.65 9 2.65 9 850139172 0.48 0.99 28.99 282.16 0.39 0.21 0.19 0 good 0 62.61 0 -0.06 0.23
951775236 8.77363 40 0 0.14 8.78 4.72 0.96 0.52 236.67 10 4.29 10 850139172 0.51 0.99 32.22 78.77 0.74 0.22 0 0 good 0.34 68.21 0 -0.11 0.01
951775243 4.58635 70 0 0.08 4.59 2.8 0.96 0.65 95.78 11 1.69 11 850139172 0.55 0.99 38.02 245.6 0.24 0.23 0.5 0 good -0.27 63.22 0 -0.04 0.08
951775249 2.43449 60 0 0.16 2.43 3.68 0.88 0.55 90.18 12 2.31 12 850139174 0.97 0.99 15.88 383.18 0.3 0.15 0.5 0 good 0.48 48.12 0 -0.03 0.07
951775254 4.44902 50 0 0.07 4.45 4.32 0.94 1.51 107.03 13 2.66 13 850139174 1.09 0.99 16.11 255.79 0.06 0.85 0.05 0 good -0.27 58.42 0 nan 0.02
951775260 5.00383 50 0 0.16 5 4.75 0.96 1.52 108.35 14 2.65 14 850139174 1.19 0.99 22.12 179 0.04 0.82 0.01 0 good 0.96 62.27 0 -0.06 0.06
951775265 4.27996 60 -0.34 0.11 4.28 4.43 0.89 0.62 98.17 15 2.62 15 850139178 0.25 0.99 34.99 172.12 0.3 0.26 0.02 0 good 0.27 57.09 0 -0.03 0.04
951775271 10.4868 60 0.34 0.09 10.49 4.14 0.98 0.54 143.06 16 3.8 16 850139178 0.28 0.99 27.71 84.99 0.47 0.21 0 0 good 0.48 73.74 0 -0.05 0.02
951775279 7.32362 60 0.21 0.24 7.32 6.54 1 0.56 205.99 17 4.31 17 850139180 0.4 0.99 30.27 87.51 0.62 0.21 0 0 good 0.34 103.5 0 -0.11 0.02
951775285 11.3536 60 -0.21 0.21 11.36 5.12 1 0.56 141.95 18 3.45 18 850139180 0.38 0.99 30.86 84.86 0.42 0.25 0 0 good 1.03 108.7 0 -0.06 0
951775292 7.47914 50 -0.69 0.23 7.48 5.36 0.98 0.52 163.58 19 4.06 19 850139180 0.32 0.99 17.75 83.2 0.6 0.19 0 0 good -0.34 107.48 0 -0.09 0
951775297 3.22563 100 -0.34 0.14 3.23 2.28 0.56 0.69 78.21 20 1.98 20 850139180 0.32 0.99 22.62 303.27 0.18 0.36 0.5 0.01 good 0.02 41.95 0.02 -0.03 0.16
951775303 4.19481 80 -0.82 0.01 4.2 2.87 0.79 0.6 99.17 21 2.18 21 850139180 0.33 0.99 24.42 179.34 0.27 0.25 0.18 0.01 good -0.14 51.35 0.01 -0.05 0.21
951775309 10.7328 60 -0.34 0.21 10.73 4.09 0.84 0.63 126.18 22 2.61 22 850139182 0.68 0.99 22.27 108.23 0.35 0.22 0.06 0.02 good 1.1 69.24 0.01 -0.06 0.24
951775314 7.63786 70 0 0.05 7.64 3.73 0.8 0.63 132.87 23 2.8 23 850139182 0.75 0.99 31.08 118.5 0.36 0.19 0.03 0.01 good 0.48 51.65 0.02 -0.08 0.15
951775321 5.68471 80 -0.48 0.04 5.69 2.32 0.64 1.39 98.06 24 2.08 24 850139182 1.01 0.99 17.81 247.21 0.04 0.81 0.5 0.01 good 0.14 43.89 0.03 -0.03 0.28
951775327 9.05005 80 -0.41 0.15 9.05 5.14 0.99 0.62 135.53 25 3.43 25 850139184 0.63 0.99 25.25 97.11 0.39 0.19 0 0 good 0.41 79.51 0 -0.06 0.02
951775333 4.2221 90 -0.34 0.05 4.22 2.52 0.55 0.59 87.52 26 2.3 26 850139188 0.54 0.99 10.81 224.2 0.2 0.33 0.5 0.01 good 0.27 41.55 0.02 -0.04 0.28
951775339 7.25025 60 -0.34 0.1 7.25 5.24 0.97 0.6 137.46 27 3.47 27 850139188 0.42 0.99 16.49 74.17 0.44 0.19 0.01 0 good 0.62 77.01 0 -0.07 0.03
951775345 2.67268 80 -0.89 0.11 2.67 3.85 0.86 0.59 116.55 28 2.87 28 850139188 0.42 0.99 19.29 202.55 0.35 0.21 0 0 good 0.62 49.24 0.01 -0.06 0.05
951775351 1.50984 50 -0.69 0.33 1.51 6.86 0.97 0.58 239.47 29 4.78 29 850139190 0.53 0.93 5.67 55.82 0.85 0.14 0 0 good 0 74.04 0 -0.1 0
951775355 3.66739 100 -0.31 0.1 3.67 2.6 0.8 0.62 80.07 30 2.27 30 850139192 0.72 0.99 22.53 190.19 0.2 0.25 0.42 0 good 0.76 43.22 0.02 -0.03 0.14
951775363 10.0034 80 -0.27 0.06 10.01 4.19 0.97 0.55 96.89 31 2.06 31 850139190 0.79 0.99 24.82 104.44 0.28 0.16 0.02 0 good 1.65 89.45 0 -0.03 0.04
951775369 4.31685 60 -0.69 0.23 4.32 4.8 0.99 0.18 107.26 32 2.5 32 850139192 1.18 0.99 40.34 162.57 0.43 0.21 0 0 good 0.07 75.41 0 -0.33 0
951775375 6.58642 80 -0.96 0.07 6.59 3.02 0.85 0.58 90.94 33 2.39 33 850139196 0.45 0.99 21.71 131.16 0.23 0.3 0.5 0.01 good 0.21 54.91 0.01 -0.04 0.12
951775380 11.8742 70 -1.17 0.29 11.88 9.95 1 0.51 197.55 34 5.26 34 850139196 0.47 0.99 27.33 69.06 0.63 0.25 0 0 good 0.34 167.27 0 -0.09 0
951775385 4.25516 80 -0.41 0.08 4.26 2.66 0.86 0.56 86.52 35 2.36 35 850139196 0.38 0.99 17.18 162.69 0.25 0.25 0.05 0.01 good 0.48 60.04 0 -0.04 0.07
951775392 12.3145 70 -0.62 0.18 12.32 5.67 0.98 0.58 161.47 37 3.7 36 850139198 0.56 0.99 28.51 80.4 0.45 0.25 0 0 good 0 84.33 0 -0.07 0.08
951775397 3.13004 60 0.21 0.14 3.13 5.07 0.97 0.58 150.94 38 3.26 37 850139198 0.5 0.99 27.52 120.31 0.46 0.16 0 0 good 0.69 74.44 0 -0.09 0.01
951775403 2.64674 50 -0.34 0.09 2.65 3.44 0.65 0.6 133.25 39 3 38 850139198 0.55 0.99 13.83 145.32 0.41 0.18 0.03 0 good 0 39.4 0.02 -0.07 0.22
951775407 2.80278 80 -0.55 0.09 2.8 3.04 0.77 1.07 93.08 40 2.01 39 850139190 1.06 0.99 23.41 316.02 0.04 0.85 0.5 0 good 0.48 50.56 0.01 -0 0.14
951775412 11.3512 60 -1.03 0.05 11.35 3.97 0.97 0.54 116.69 41 2.74 40 850139198 0.55 0.99 24.43 106.77 0.36 0.23 0.01 0.01 good -0.27 92.73 0 -0.04 0.29
951775417 5.77244 70 -0.34 0.16 5.77 3.68 0.98 0.6 149.48 42 2.58 41 850139204 0.79 0.99 27 101.09 0.45 0.19 0 0 good 1.03 68.98 0 -0.05 0.06
951775423 3.63814 60 -1.03 0.15 3.64 3.59 0.98 0.54 142.1 43 3.4 42 850139202 0.23 0.99 19.97 137.1 0.52 0.18 0 0 good 1.03 66.94 0 -0.08 0.01
951775429 8.45359 70 -0.69 0.12 8.46 3.3 0.95 0.54 147.32 44 2.61 43 850139204 0.68 0.99 15.38 114.19 0.48 0.16 0 0 good 0.55 74.04 0 -0.06 0.04
951775435 0.12783 90 -0.48 0.05 0.13 2.28 0 1.26 102.53 45 1.69 44 850139204 1.24 0.96 30.13 122.94 0.05 0.93 0.13 0 good 0.76 27.82 0.01 -0 0
951775441 15.7157 50 -1.37 0.22 15.72 7.37 1 0.6 268.44 46 5.02 45 850139204 0.65 0.99 16.43 39.59 0.8 0.29 0 0 good 1.03 105.12 0 -0.11 0
951775448 5.67954 60 -0.41 0.05 5.68 4 0.96 0.54 166.1 47 2.99 46 850139204 0.74 0.99 27.5 104.69 0.51 0.15 0.01 0 good 0.69 71.28 0 -0.08 0.05
951775453 2.09172 10 nan 0.19 2.09 7.41 1 1.65 86.57 49 2.49 47 850139206 0.83 0.69 22.75 394.3 0.02 nan 0.46 0 noise nan 121.16 0 nan 0.27
951775465 3.09677 80 -0.48 0.13 3.1 3 0.88 0.71 85.73 50 2.33 48 850139206 0 0.99 16.69 269.74 0.22 0.4 0.5 0 good 0.82 47.57 0.01 -0.03 0.43
951775472 1.61307 40 -0.34 0.09 1.61 5.62 0.93 0.25 92.82 51 2.58 49 850139206 0.13 0.82 9.54 167.4 0.38 0.15 0.5 0 good 0.69 63.28 0 -0.03 1.71
951775477 4.29391 60 -0.34 0.17 4.29 6.76 1 0.54 113.36 52 2.89 50 850139202 0.18 0.99 24.36 139.27 0.41 0.19 0 0 good 0.27 93.31 0 -0.05 0.01
951775484 2.01732 30 0 0.21 2.02 6.83 1 0.3 70.65 53 2.11 51 850139210 230.44 0.85 25.65 566.09 0.27 0.14 0.06 0 good 8.24 100.03 0 -0.01 32.23
951775489 2.53524 80 -0.27 0.13 2.54 3.03 0.79 0.62 80.95 54 2.48 52 850139210 0.75 0.99 17.12 249.23 0.24 0.16 0.13 0 good 0.34 49.54 0.01 -0.04 0.05
951775496 3.5313 60 0.34 0.07 3.53 4.04 0.97 0.52 75.7 55 2.31 53 850139210 0.92 0.99 18.47 346.15 0.26 0.11 0.04 0 good 1.1 66.67 0 -0.04 0.02
951775502 8.72495 70 -0.48 0.14 8.73 5.01 0.97 0.6 93.73 56 2.96 54 850139212 0.36 0.99 19.35 85.45 0.24 0.33 0.01 0 good 1.03 77.38 0 -0.06 0.02
951775508 0.58591 90 -0.55 0.03 0.59 2.26 0.2 0.6 63.48 57 2.04 55 850139212 0.26 0.99 21.29 536.46 0.14 0.37 0.19 0 good -0.34 35.5 0.01 -0.04 0
951775515 7.21904 70 -0.55 0.1 7.22 5.47 0.99 0.63 75.23 58 2.41 56 850139214 0.56 0.99 14.55 122.84 0.2 0.29 0.17 0 good 1.03 89.39 0 -0.04 0.1
951775522 4.06905 50 0 0.11 4.07 4.75 0.93 1.35 93.48 59 1.92 57 850139216 1.13 0.99 23.25 185.95 0.03 1.36 0.01 0 good 0.34 63.21 0 -0 0.02
951775529 9.18253 70 -0.41 0.21 9.18 6.49 1 0.54 207.48 60 4.42 58 850139216 0.61 0.99 29.09 88.7 0.72 0.15 0 0 good -0.07 101.9 0 -0.09 0.01
951775535 4.03723 100 -0.27 0.09 4.04 2.45 0.64 1.28 93.42 61 2.02 59 850139216 1.49 0.99 12.57 255.82 0.04 0.96 0.5 0 good 0.07 41.65 0.03 -0.02 0.21
951775542 0.60586 170 -0.31 0.11 0.61 2.4 0.51 0.7 54.33 62 1.07 60 850139216 3.39 0.98 45.2 690.72 0.05 0.36 0.5 0 noise -0.15 40.99 0.01 -0.09 18.78
951775550 12.0122 60 0 0.24 12.01 6.16 1 0.59 178.97 63 4.69 61 850139218 0.67 0.99 27.44 85.49 0.5 0.19 0 0 good 0.69 113.78 0 -0.09 0
951775556 17.1874 20 nan 0.06 17.19 4.6 0.99 0.22 74.77 64 1.92 62 850139218 0.54 0.96 21.77 233.63 0.29 0.07 0.21 0 good 0 99.31 0 -0.04 0.01
951775561 0.58271 90 0.06 0.07 0.58 2.91 0.18 1.48 56.54 65 1 63 850139218 2.15 0.99 30.13 586.42 0.01 1 0.11 0 good 1.17 37.78 0.01 nan 0.23
951775569 7.29985 60 0 0.04 7.3 2.52 0.96 0.56 95.33 66 2.46 64 850139218 0.61 0.99 24.61 103.05 0.31 0.16 0.08 0 good 0 68.79 0 -0.04 0.03
951775576 6.64046 70 -0.41 0.04 6.64 3.24 0.92 1.41 102.86 67 2.25 65 850139216 1.24 0.99 31.71 132.11 0.05 1.02 0 0 good -0.41 58.63 0.01 -0.08 0.06
951775582 11.2056 70 0.07 0.12 11.21 4.38 0.94 0.51 94.58 68 2.75 66 850139220 0.45 0.99 21.02 108.08 0.3 0.21 0.08 0 good 0.34 75.73 0 -0.03 0.03
951775589 3.70862 60 -0.69 0.12 3.71 3.94 0.84 0.59 83.87 69 2.26 67 850139220 0.55 0.99 14.05 133.01 0.24 0.18 0.04 0 good 1.03 48.83 0.01 -0.03 0.14
951775595 8.77259 60 -1.58 0.12 8.77 5.14 0.99 0.56 111.16 70 3.2 68 850139222 0.93 0.99 19.28 62.18 0.32 0.16 0 0 good 0 75.21 0 -0.05 0
951775602 0.10995 100 -0.08 nan 0.11 2.73 0 1.24 62.96 71 1.91 69 850139226 3.83 0.98 29.72 42.53 0.03 1.06 0.5 0 good 0.14 29.57 0.01 -0 0
951775607 8.06443 70 -0.82 0.29 8.07 8.78 1 0.63 131.83 72 2.76 70 850139230 0.96 0.99 25.83 106.65 0.39 0.21 0 0 good 0.34 129.14 0 -0.05 0
951775614 6.70484 50 -0.69 0.38 6.71 10.65 1 0.6 196.48 73 5.66 71 850139228 0.31 0.99 21.75 60.06 0.6 0.21 0 0 good 0.69 160.23 0 -0.09 0
951775620 5.07875 100 -0.32 0.11 5.08 3.51 0.94 0.65 65.71 74 2.18 72 850139228 0.3 0.99 21.02 239.5 0.16 0.33 0.5 0 good 1.1 57.91 0 -0.02 0.14
951775627 0.02242 100 0.08 nan 0.02 2.83 0 1.4 73.7 75 1.6 73 850139230 4.23 0.71 nan 0 0.02 nan 0.35 0 good 0.89 34.12 0 -0.03 0
951775633 11.1431 40 -2.75 0.23 11.15 3.79 0.97 0.56 182.87 76 3.83 74 850139236 0.94 0.99 12.99 70.51 0.55 0.19 0.02 0 good -1.03 91.5 0 -0.09 0.02
951775639 5.2942 50 -0.69 0.09 5.3 3.44 0.98 1.43 60.95 77 1.48 75 850139236 2.95 0.99 24.66 209.82 0.01 nan 0.31 0 good -1.03 85.46 0 -0.02 0.02
951775645 6.28933 70 -1.72 0.12 6.29 3.72 0.9 1.35 76.24 79 1.76 76 850139230 2.03 0.99 19.58 146.74 0.04 2.31 0.09 0 good -0.82 57.89 0.01 -0.05 0.09
951775648 11.3501 20 nan 0.07 11.35 4.61 0.94 1.5 84.66 80 2.4 77 850139238 1.69 0.99 10.29 92.65 0.04 1.06 0.19 0.01 good 0.69 94.72 0 nan 0.19
951775655 4.79406 40 0 0.14 4.79 4.51 0.92 0.59 113.46 81 2.83 78 850139242 0.13 0.99 16.47 100.81 0.38 0.26 0 0 good -0.34 61.26 0 -0.06 0.06
951775660 9.35944 50 -0.21 0.21 9.36 6.05 1 0.55 246.85 82 6.11 79 850139240 0.5 0.99 21.52 81.08 0.76 0.18 0 0 good 0.69 90.51 0 -0.12 0
951775666 11.0597 40 -1.03 0.17 11.06 4.43 0.99 0.58 160.19 83 3.94 80 850139240 0.44 0.99 21.8 83.21 0.52 0.18 0 0 good -0.69 107.51 0 -0.07 0.01
951775671 8.41691 60 -0.41 0.16 8.42 5.66 1 0.49 145.55 84 3.68 81 850139240 0.46 0.99 15.76 67.18 0.5 0.16 0 0 good 0 129.49 0 -0.08 0
951775678 3.69808 70 -1.03 0.06 3.7 2.37 0.77 0.71 79.33 85 2.03 82 850139242 0.02 0.99 22 225.58 0.18 0.34 0.5 0 good -0.07 42.86 0.02 -0.03 0.25
951775684 2.12748 50 -0.69 0.3 2.13 4.26 0.98 0.66 185.06 86 3.99 83 850139248 0.72 0.99 10.2 87.05 0.55 0.21 0 0 good 1.37 78.5 0 -0.08 0.01
951775689 13.6246 40 -1.03 0.22 13.63 6.02 1 0.56 178.31 87 4.12 84 850139248 0.79 0.99 15.17 64.83 0.46 0.15 0 0 good -0.69 131.43 0 -0.07 0.01
951775695 1.63064 20 0 0.14 1.63 4.44 0.99 0.21 117.36 88 2.77 85 850139248 0.58 0.76 7.91 115.03 0.48 0.1 0.5 0 good nan 89.39 0 -0.1 0.29
951775702 14.4631 70 -0.69 0.21 14.47 6.35 0.99 0.6 158.77 89 4.06 86 850139248 0.69 0.99 19.46 83.27 0.43 0.22 0 0 good -0.34 133.76 0 -0.09 0.01
951775708 15.7992 40 -2.06 0.21 15.8 6.55 1 0.65 95.3 90 2.8 87 850139254 0.68 0.99 4.87 57.42 0.27 0.23 0.05 0 good 0.34 137.15 0 -0.04 0.15
951775714 3.70376 40 -0.69 0.1 3.7 3.89 0.99 0.3 100.81 91 2.57 88 850139254 0.72 0.99 10 141.97 0.44 0.12 0 0 good 0.34 60.43 0 -0.07 0
951775720 5.57476 80 -0.24 0.14 5.58 2.8 0.72 0.62 69.47 92 1.22 89 850139260 0.42 0.99 15.36 189.8 0.14 1.11 0.5 0.01 good 0.34 47.77 0.03 -0.04 0.14
951775726 9.92344 60 -0.27 0.05 9.93 3.78 0.88 0.47 92.79 93 1.55 90 850139260 0.28 0.99 15.49 116.95 0.27 0.92 0.41 0.02 good -0.69 66.54 0.02 -0.07 0.23
951775733 0.47348 60 -0.21 0.11 0.47 2.98 0.47 1.3 70.35 94 2.08 91 850139262 1.79 0.99 24.86 456.96 0.04 0.87 0.02 0 good 0 42.76 0.01 -0 0.17
951775738 1.0131 40 0.34 0.04 1.01 4.16 0.93 1.19 72.03 95 2.03 92 850139262 1.44 0.99 22.13 468 0.05 1 0.5 0 good -1.37 58.68 0 -0 0
951775741 4.01666 40 -0.82 0.29 4.02 4.86 0.98 0.7 186.62 96 5 93 850139264 0.46 0.99 27.81 59 0.55 0.21 0 0 good nan 59.04 0.01 -0.09 0.01
951775745 9.23078 40 -0.34 0.08 9.23 2.53 0.88 0.67 85.07 97 2.59 94 850139264 0.48 0.99 20.38 119.26 0.24 0.22 0.13 0.01 good -0.69 57.55 0.02 -0.06 0.08
951775748 3.94433 110 -0.1 0.08 3.95 2.42 0.61 0.67 63.39 98 1.96 95 850139264 0.66 0.99 13.92 212.85 0.12 0.33 0.5 0.01 good -0.31 40.5 0.06 -0.03 0.13
951775751 6.06096 60 -0.55 0.06 6.06 4.13 0.92 0.63 72.23 99 1.19 96 850139272 0.52 0.99 20.51 148.37 0.2 nan 0.07 0.01 good 1.37 55.26 0.02 -0.03 0.09
951775754 6.40713 60 -1.37 0.22 6.41 7.43 0.99 0.67 100.25 100 3.84 97 850139274 0.39 0.99 24.91 75.06 0.25 0.27 0 0 good 0.27 102.82 0 -0.03 0
951775759 4.98223 50 -0.69 0.12 4.98 2.77 0.95 0.65 72.15 101 0.89 98 850139278 0.46 0.99 22.51 222.68 0.19 1.17 0.23 0.01 good 0 69.15 0 -0.02 0.07
951775764 3.11888 70 -0.76 0.09 3.12 1.87 0.5 0.63 62.84 102 1.93 99 850139276 0.48 0.99 27.47 222.75 0.16 0.25 0.44 0.01 good 1.03 36.7 0.06 -0.03 0.18
951775770 12.4008 70 -0.55 0.06 12.4 3.47 0.95 0.59 60.86 103 1.93 100 850139276 0.54 0.99 26.27 125.01 0.14 0.34 0.14 0.04 good -1.03 83.23 0.01 -0.02 0.06
951775776 4.19047 50 -1.72 0.24 4.19 7.91 1 0.67 129.49 104 3.74 101 850139276 0.23 0.99 21.69 97.77 0.46 0.16 0 0 good 0 106.03 0 -0.04 0
951775782 4.02462 70 -0.69 0.14 4.03 4 0.89 1.24 62.31 105 2.12 102 850139280 1.14 0.99 14.7 177.02 0.03 1.74 0.1 0.01 good 2.59 76.73 0.01 -0 0.01
951775789 0.05745 70 -1.1 0.11 0.06 2.27 0 1.35 63.31 106 2.12 103 850139280 1.41 0.85 7.15 7.15 0.02 1.22 0.49 0 good 0 27.25 0.02 -0.02 0
951775795 9.85834 40 -3.43 0.36 9.86 11.63 1 0.82 214.98 107 5.25 104 850139282 0.87 0.99 20.3 44.76 0.26 0.32 0 0 good -0.69 186.47 0 -0.09 0
951775800 0.03658 70 -3.98 nan 0.04 2.82 0 1.47 81.41 108 1.46 105 850139282 2.13 0.86 1 0 0.03 1.06 0.3 0 good 4.4 29.55 0.01 nan 0
951775806 4.49077 40 -0.69 0.17 4.49 4.55 0.97 0.12 82.01 109 2.13 106 850139286 1.21 0.99 19.28 144.09 0.2 0.12 0 0 good 0.34 76.42 0 -0.23 0.01
951775813 1.23269 100 -0.82 0.11 1.23 2.89 0.8 1.28 55.51 110 1.44 107 850139282 6.97 0.99 21.55 425.28 0.03 nan 0.5 0 good 0.22 48.83 0.01 -0.02 0.31
951775819 0.663 60 -0.76 0.16 0.66 4.64 0.72 0.6 69.76 111 1.47 108 850139294 0.17 0.99 20.51 336.47 0.16 0.29 0.02 0 good 0 46.16 0.01 -0.01 0
951775826 7.01712 60 -0.69 0.17 7.02 5.8 1 1.37 91.02 112 2.84 109 850139292 1.28 0.99 11.04 96.21 0.04 1.4 0 0 good 0.96 106.46 0 -0.02 0.01
951775830 0.03823 80 0 nan 0.04 2.21 0.11 0.62 49.99 113 1.49 110 850139296 0.33 0.57 17 36.63 0.14 1.02 0.09 0 good 0.89 30.99 0.01 -0.02 0
951775836 1.6696 50 0 0.18 1.67 4.3 0.98 0.7 88.51 114 3.14 111 850139298 0.62 0.99 13.94 233.35 0.28 0.14 0 0 good 0.96 77.02 0 -0.04 0.01
951775843 5.1145 70 -1.24 0.24 5.12 9.92 1 0.67 144.07 115 4.94 112 850139298 0.58 0.99 19.67 53.24 0.43 0.22 0 0 good 0.62 164.83 0 -0.07 0
951775849 1.22205 60 -0.69 0.31 1.22 7.58 0.99 0.69 151.24 116 4.45 113 850139302 0.8 0.99 11.8 110.74 0.41 0.15 0 0 good -1.03 80.79 0 -0.08 0
951775857 1.93197 90 -0.34 0.15 1.93 4.22 0.94 1.4 58.35 117 1.89 114 850139302 2.08 0.99 13.57 344.22 0.03 1.1 0.09 0 good 1.37 66.73 0 -0.05 0.08
951775863 2.86612 50 -3.09 0.08 2.87 4.26 0.93 1.26 64.67 118 2.05 115 850139302 1.48 0.99 20.08 207.57 0.03 1.26 0.03 0 good 0.34 60.44 0.01 -0.01 0.07
951775869 2.13171 80 -0.84 0.16 2.13 4.54 0.88 0.6 94.87 119 3.11 116 850139306 0.27 0.99 16.37 159.47 0.34 0.16 0 0 good -0.34 57.64 0 -0.03 0.01
951775875 6.9637 40 -0.34 0.35 6.97 5.56 1 0.58 199.9 120 5.12 117 850139308 0.72 0.99 7.89 39.38 0.53 0.22 0 0 good 0.69 84.8 0 -0.1 0
951775880 0.03751 80 -0.48 0.08 0.04 2.26 0 1.22 69.51 121 1.77 118 850139308 2.1 0.94 nan 0 0.04 0.82 0.27 0 good 0.69 26.36 0.01 -0.01 27.52
951775885 0.56607 70 -1.65 0.31 0.57 9.86 0.99 0.66 132.13 122 4.37 119 850139316 0.32 0.59 5.22 73.43 0.46 0.15 0 0 good 1.72 107.9 0 -0.05 0
951775890 9.40997 70 0.21 0.09 9.41 3.15 0.96 0.71 56.62 123 2.11 120 850139316 0.52 0.99 15.85 143.19 0.14 0.22 0.5 0.01 good 0.27 68.5 0.01 -0.03 0.06
951775897 7.1681 20 nan 0.13 7.17 4.14 0.94 0.62 103.5 124 3.52 121 850139316 0.49 0.99 11.73 74.03 0.3 0.21 0.01 0 good 0 63.07 0.01 -0.05 0.05
951775903 7.18907 10 nan 0.13 7.19 4.6 0.99 0.25 89.52 125 3.27 122 850139316 0.25 0.99 11.93 180.45 0.36 0.1 0.22 0 noise nan 86.84 0 -0.06 0.05
951775908 10.2125 60 -0.96 0.12 10.21 4.63 0.97 0.54 62.8 126 2.46 123 850139318 0.49 0.99 21.83 139.02 0.17 0.23 0.23 0 good 1.03 93.61 0 -0.03 0.09
951775915 7.01413 50 0 0.17 7.02 5.43 0.98 0.59 92.16 127 3.55 124 850139318 0.51 0.99 13.14 75.12 0.27 0.25 0.01 0 good 1.03 78.31 0 -0.05 0.03
951775919 2.94631 60 -0.82 0.12 2.95 3.95 0.93 0.6 75.64 128 2.27 125 850139322 0.03 0.99 17.21 146.28 0.27 0.19 0.02 0 good 0 60.65 0 -0.04 0.04
951775927 6.76664 30 -3.43 0.11 6.77 6.41 1 0.23 64.71 129 2.18 126 850139322 0.2 0.91 29.8 320.46 0.26 0.15 0.5 0 good 0 121.6 0 -0.03 0.22
951775934 3.88078 70 -0.41 0.15 3.88 3.87 0.86 1.28 67.06 130 2.23 127 850139324 1.76 0.99 18.34 214.29 0.04 0.87 0 0 good 0.76 64.49 0 -0 0.03
951775940 4.93687 50 -1.37 0.13 4.94 4.69 0.95 0.66 61.4 131 2.03 128 850139326 0.01 0.99 12.77 192.83 0.17 0.33 0.39 0 good 0.41 72.86 0 -0.02 0.07
951775947 6.44878 60 -0.69 0.27 6.45 5.67 0.98 0.6 99.29 132 4.05 129 850139332 0.54 0.99 10.18 83.2 0.29 0.21 0 0 good -0.27 96.35 0 -0.05 0.01
951775954 1.10311 70 -1.03 0.21 1.1 4.92 0.9 0.7 97.96 133 3.66 130 850139328 0.76 0.99 27.84 200.91 0.26 0.16 0 0 good 0.07 55.33 0 -0.04 0.1
951775961 3.56591 70 -0.69 0.13 3.57 2.46 0.87 0.56 64.41 134 2.77 131 850139332 0.51 0.99 11.33 208.96 0.2 0.18 0.5 0 good 0.21 54.22 0.01 -0.03 0.11
951775967 3.97533 80 -0.82 0.04 3.98 3.3 0.86 1.33 59.94 135 1.56 132 850139330 239.7 0.99 15.27 223.36 0.03 nan 0.5 0 good 0.76 54.16 0.01 -0 0.09
951775974 4.69145 50 -0.34 0.09 4.69 3.5 0.75 0.59 81.19 136 3.15 133 850139334 0.33 0.99 8.33 141.12 0.25 0.19 0.42 0.02 good 0.69 54.14 0.02 -0.05 0.23
951775980 6.49197 70 -0.69 0.05 6.49 3.44 0.77 0.62 64.94 137 2.47 134 850139334 0.32 0.99 16.27 154 0.18 0.26 0.5 0.02 good 0.82 63.45 0.02 -0.03 0.16
951775985 4.92654 70 -1.44 0.24 4.93 6.31 1 0.65 151.83 138 4.29 135 850139336 0.98 0.99 23.9 111.88 0.43 0.16 0 0 good -0.34 107.38 0 -0.07 0
951775990 4.2006 50 -1.03 0.2 4.2 6.37 1 0.6 124.87 139 3.43 136 850139336 0.82 0.86 27.93 86.04 0.42 0.15 0 0 good 0 114.9 0 -0.08 0
951776000 1.76766 170 0.52 0.09 1.77 3.82 0.93 0.91 4.02 140 0.06 137 850139606 1.57 0.99 32.55 394.42 0 nan 0.07 0 noise -2.06 54.57 0.01 -0 0.09
951776007 2.56934 20 nan 0.16 2.57 5.73 1 0.23 86.16 141 2.81 138 850139338 0.45 0.95 23.94 353.78 0.34 0.07 0.06 0 noise 12.36 93.03 0 -0.04 0.03
951776014 0.04764 50 0 nan 0.05 3.16 0 0.15 122.76 142 3.53 139 850139336 3.83 0.26 6.26 21.36 0.36 0.18 0.06 0 noise -0.27 31.48 0.01 -0.27 0
951776020 2.06269 50 -0.69 0.35 2.06 7.87 0.99 0.6 187.05 143 5.52 140 850139340 0.82 0.99 16.24 57.08 0.57 0.14 0 0 good 0.69 84.65 0 -0.08 0
951776024 3.81785 70 -0.48 0.13 3.82 2.52 0.8 1.4 75.17 144 2.37 141 850139340 1.98 0.99 25.38 171.36 0.03 1.74 0.25 0.01 good 0.27 59.49 0.01 -0.08 0.09
951776031 8.76536 80 -1.44 0.13 8.77 4.87 0.98 0.65 54.17 145 1.12 142 850139342 0.51 0.99 19.6 223.66 0.13 nan 0.03 0 good -0.14 81.64 0 -0.03 0.05
951776037 10.8718 50 -0.34 0.11 10.87 5.93 0.99 0.59 101.88 146 2.73 143 850139344 0.07 0.99 27.18 80.51 0.32 0.22 0 0 good -0.34 101.11 0 -0.07 0.01
951776043 1.12409 80 -0.07 0.13 1.12 2.95 0.59 0.69 54.06 147 2.24 144 850139348 0.66 0.99 21.02 463.89 0.13 0.25 0.06 0.01 good 0.82 48.3 0.01 -0.03 0.03
951776049 4.25723 90 -0.82 0.15 4.26 2.38 0.8 0.63 61.6 148 1.98 145 850139350 0.04 0.99 12.38 233.48 0.17 0.33 0.21 0.01 good 1.85 52.08 0.02 -0.03 0.12
951776055 5.59956 50 -1.37 0.18 5.6 6.78 0.99 0.58 132.73 149 3.92 146 850139350 0.21 0.99 11.1 42.17 0.43 0.25 0 0 good 1.03 87.41 0 -0.07 0
951776061 2.47872 60 0 0.06 2.48 2.85 0.7 0.67 73.14 150 2.22 147 850139350 0.06 0.99 37.3 274.56 0.23 0.27 0.19 0.01 good 1.03 43.94 0.03 -0.03 0.08
951776067 4.50431 70 -0.34 0.05 4.51 2.47 0.87 0.63 73.23 151 2.22 148 850139350 0.09 0.99 17.73 142.16 0.21 0.32 0.05 0.01 good 0.96 57.9 0.01 -0.03 0.16
951776074 4.13591 30 0 0.21 4.14 8.77 1 0.62 133.24 152 4.15 149 850139352 0.22 0.99 27.42 63.18 0.46 0.25 0 0 good nan 113.87 0 -0.05 0
951776080 6.05755 60 -0.69 0.08 6.06 2.92 0.91 0.66 69.73 153 2.53 150 850139352 0.08 0.99 15.46 172.28 0.2 0.25 0.13 0.01 good 1.72 63.57 0.01 -0.04 0.33
951776085 3.87726 80 0.82 0.09 3.88 3.35 0.84 0.6 56.47 154 1.39 151 850139358 0.44 0.99 29 230.02 0.19 1.02 0.22 0.01 good 1.51 55.51 0.01 -0.02 0.24
951776091 3.25219 50 0.69 0.03 3.25 3.13 0.55 0.71 76.61 155 1.92 152 850139358 0.33 0.99 15.38 179.6 0.23 0.95 0.18 0.01 good 1.58 43.2 0.03 -0.04 0.29
951776096 3.20424 40 0 0.03 3.2 4.58 0.77 0.62 106.25 156 2.87 153 850139358 0.21 0.99 10.89 109.47 0.3 0.33 0.01 0.01 good 1.03 52.27 0.02 -0.05 0.23
951776100 2.1993 70 -0.62 0.07 2.2 3.45 0.64 0.63 74.2 157 2.23 154 850139360 0.38 0.99 30.81 375.56 0.22 0.21 0.17 0.01 good 0.48 41.7 0.03 -0.03 0.31
951776106 0.33336 30 0 0.06 0.33 5.42 0.97 0.3 88.13 158 2.85 155 850139360 0.22 0.92 20.1 229.42 0.37 0.12 0.17 0 noise 0 56.77 0 -0.05 0
951776112 1.66009 60 -1.03 0.05 1.66 4.05 0.77 0.67 68.67 159 0.64 156 850139364 0.27 0.99 11.77 217.45 0.21 0.91 0.34 0 noise 1.37 52.72 0.01 -0.04 0.44
951776117 28.7194 70 -0.34 0.11 28.72 3.24 0.9 0.34 64.86 160 2.38 157 850139366 0.33 0.99 12.13 95.39 0.27 0.21 0.27 0.06 good 0.21 140.35 0.04 -0.06 0.02
951776124 2.19186 50 -1.37 0.1 2.19 3.12 0.7 0.56 49.08 161 1.29 158 850139362 0.65 0.99 31.56 324.59 0.09 0.26 0.5 0 good 0.21 37.34 0.05 -0.01 0.06
951776129 0.12648 50 -0.34 0.02 0.13 3.04 0.27 1.22 70.78 162 1.69 159 850139368 2.06 0.99 22.09 79.5 0.03 2.44 0.37 0 good 0.34 31.98 0.02 -0.02 0
951776135 7.08915 50 -0.14 0.14 7.09 3.93 1 1.32 55.44 163 1.95 160 850139372 2.13 0.99 24.66 156.95 0.03 0.99 0.44 0 good 1.37 92.56 0 -0.01 0.06
951776142 6.08607 40 -0.34 0.16 6.09 6.93 1 0.62 121.08 164 4.14 161 850139372 0.96 0.99 21.15 66.32 0.35 0.15 0 0 good -0.69 103.35 0 -0.08 0
951776147 12.7011 60 0 0.05 12.7 3.19 0.83 0.38 59.27 165 2.64 162 850139374 0.45 0.99 29.64 122.62 0.22 0.16 0.5 0.04 good 0 44.69 0.16 -0.04 0.02
951776152 1.01786 60 -0.69 0.09 1.02 3.11 0.67 0.63 53.62 166 1.59 163 850139376 0.32 0.99 22.81 390.81 0.17 0.92 0.08 0 good 1.37 35.32 0.06 -0.02 0.15
951776159 1.14196 40 0 0.25 1.14 7.68 0.99 0.59 101.76 167 3.16 164 850139384 0.54 0.99 6.43 184.8 0.34 0.16 0 0 good 1.37 85.31 0 -0.05 0.03
951776165 2.34851 30 -2.06 0.12 2.35 4.26 0.92 0.15 77.29 168 2.5 165 850139388 1.63 0.99 26.16 384.5 0.24 0.21 0.02 0 noise 0.69 73.29 0.01 -0.25 0.03
951776170 1.31237 120 0.01 0.03 1.31 3.8 0.92 1.09 46.15 169 1.55 166 850139388 6.18 0.99 34.92 564.8 0.01 nan 0.5 0 noise 0.76 56.17 0.01 0 1.96
951776176 0.01395 70 -0.35 nan 0.01 3.62 0.11 0.44 52.14 170 1.88 167 850139390 0.79 0.35 8.56 11.11 0.19 0.16 0.2 0 good 1.37 45.96 0 -0.05 0
951776182 2.65387 20 nan 0.19 2.65 nan nan 0.43 79.4 171 3.33 168 850139400 0.33 0.99 16.6 259.5 0.29 0.19 0.16 0 good 0.69 nan nan -0.04 0.06
951776188 7.58506 30 1.37 0.16 7.59 nan nan 0.3 66.46 172 2.4 169 850139402 0.5 0.99 15.87 356.08 0.28 0.15 0 0 good 1.37 nan nan -0.01 0.01
951776194 1.39235 10 nan 0.15 1.39 nan 1 1.36 34.61 173 1.4 170 850139436 0.11 0.99 13.9 337.65 0.05 0.67 0.07 nan noise nan nan nan -0 12.82
951776200 3.31594 120 1.58 0.02 3.32 nan nan 0.03 22.26 174 0.61 171 850139476 45.58 0.99 71.66 1159.19 0.41 nan 0.5 0 noise 0.96 nan nan nan 0.4
951776206 2.21232 100 2.06 0.02 2.21 1.37 0.21 2.09 20.63 175 0.49 172 850139476 3.1 0.99 42.55 1044.42 0 2.17 0.5 0.06 noise -4.4 30.65 0.15 -0.31 1.23
951776213 3.47467 90 -1.37 0.13 3.48 5.88 0.99 0.44 44.17 176 1.25 173 850139488 0.89 0.99 10.85 256.33 0.14 0.15 0.13 0.01 good 8.83 94.87 0.01 -0.02 0.45
951776217 1.15323 50 0 0.09 1.15 5.8 0.98 0.62 57.58 177 1.79 174 850139486 0.13 0.99 20.48 464.03 0.21 0.16 0.04 0 noise -1.24 62.38 0.01 -0.01 2.42
951776225 2.83533 170 2.72 0.02 2.84 2.27 0.45 2.07 28.09 178 0.56 175 850139488 13.22 0.99 48.95 1265.54 0.01 1.33 0.5 0.06 noise -0.06 38.34 0.11 -0.21 0.38
951776231 1.63539 40 nan 0.2 1.64 5.69 0.99 0.73 82.15 179 2.16 176 850139494 0.83 0.99 28.59 297.98 0.22 0.11 0.04 0 good -0.69 75.49 0 -0.03 0.17
951776237 4.36801 80 0.55 0.1 4.37 4.62 0.99 0.12 66.59 180 1.06 177 850139496 3.06 0.99 26.5 406.17 0.09 0.55 0.5 0 good 12.77 81.51 0.01 -0.26 3.03
951776243 0.02015 120 2.68 nan 0.02 2.69 0.05 1.83 68.82 181 0.68 178 850139494 5.98 0.75 nan 0 0.02 2.4 0.41 0 noise 0.41 18.23 0.1 -0.05 286.11
951776249 0.1333 60 -0.76 nan 0.13 5.41 0.9 0.69 146.4 182 1.97 179 850139496 0.64 0.99 16 39.46 0.54 0.1 0.01 0 good 0.34 54.6 0 -0.07 2.18
951776255 0.86006 90 -0.07 0.14 0.86 4.42 0.93 1.54 65.25 183 0.87 180 850139496 3.24 0.99 13.37 493.86 0.06 1.85 0.12 0 good 6.26 48.86 0.01 -0.22 5.08
951776262 1.76591 40 -0.69 0.35 1.77 7.8 1 0.23 282.78 184 4.74 181 850139498 0.13 0.97 17.64 61.64 1.07 0.1 0 0 good 0 164.19 0 -0.05 0
951776268 0.69349 40 0.69 0.11 0.69 4.24 0.9 0.11 94.99 185 1.76 182 850139498 3.7 0.98 21.19 268.14 0.24 0.1 0.01 0 good -0.69 58.21 0 -0.13 0.64
951776273 2.10133 100 0.02 0.19 2.1 4.2 0.98 1.8 113.98 186 1.66 183 850139506 1.22 0.99 25.37 287.55 0.09 0.63 0.01 0 good 0 59.17 0.01 -0.02 0.6
951776281 2.41527 60 -0.34 0.14 2.42 5.06 1 1.69 69.81 187 1.23 184 850139502 1.7 0.99 18.76 230.28 0.04 0.76 0.02 0 good 0.55 78.42 0 -0.14 0.43
951776286 5.27199 60 0 0.16 5.27 7.05 1 0.21 192.23 188 3.42 185 850139506 0.31 0.99 30.77 70.75 0.81 0.12 0 0 good -0.14 109.92 0 -0.05 0
951776292 0.29006 60 0 -0 0.29 2.71 0.72 0.58 118.3 189 1.09 186 850139510 0.56 0.99 28.07 239.12 0.46 0.12 0.18 0 good 1.3 22.69 0.25 -0.07 57.99
951776299 2.34386 150 -1.29 0.02 2.34 1.44 0.17 1 35.5 190 0.28 187 850139510 14.76 0.99 50.65 976.93 0.01 1.52 0.29 0.04 noise 1.19 25.26 0.29 nan 2.59
951776306 3.13056 150 -0.21 -0.01 3.13 nan nan 0.03 29.51 191 0.45 188 850139514 4.46 0.99 55.06 933.2 0.33 nan 0.5 0 noise 0.66 nan nan nan 0.28
951776311 0.47865 150 4.64 0.01 0.48 nan nan 2.09 144.25 192 1.43 189 850139510 1.95 0.99 94.65 1997.13 0.03 1.36 0.11 0 noise -8.42 nan nan -2.48 0.51
951776317 2.72466 160 0.38 0.02 2.73 nan nan 1.96 39.14 193 0.73 190 850139510 3.03 0.99 57.56 1389.15 0.02 1.47 0.5 0 noise -7.06 nan nan -0.55 0.18
951776323 0.41438 160 -0.21 0.03 0.41 1.76 0.03 1.76 73.44 194 0.56 191 850139510 0.42 0.99 47.24 1346.8 0.02 1.4 0.08 0 noise 5.06 14.92 0.43 -0.59 2.48
951776329 0.17257 50 0 0.12 0.17 5.37 0.87 0.65 167.58 195 2.19 192 850139518 0.47 0.98 14.47 61.94 0.68 0.11 0.02 0 good 0 38.61 0.04 -0.09 29.94
951776333 3.40068 140 -3.67 0.04 3.4 2.84 0.72 1.65 32.64 196 0.7 193 850139518 9.36 0.99 16.01 446.36 0.05 1.48 0.5 0.04 noise -0.49 39.91 0.13 -0.04 2.29
951776339 2.95179 170 -0.61 0.02 2.95 2.56 0.5 0.36 28.68 197 0.56 194 850139520 0.57 0.99 67.2 574.31 0.12 0.23 0.5 0.03 good 3.56 30.9 0.24 -0.01 7.6
951776345 5.67582 120 -1.37 0.08 5.68 4.54 0.92 0.37 58.44 198 1.41 195 850139522 0.79 0.99 30.85 342.96 0.22 0.08 0.02 0 good 0.76 48.17 0.09 -0.02 0.17
951776352 0.08835 170 0.58 nan 0.09 3.23 0.09 1.17 22.08 199 0.73 196 850139526 4.23 0.9 43.42 52.31 0.01 nan 0.12 0 noise -0.01 26.01 0.07 0 4.96
951776358 1.60532 170 0.57 -0.04 1.61 1.44 0.11 2.25 43.08 200 0.62 197 850139510 2.87 0.99 26.31 901.74 0.01 1.11 0.44 0.03 noise -8.49 24.28 0.31 -0.62 2.06
951776364 3.15164 100 -5.59 0.01 3.15 1.54 0.44 2.09 30.77 201 0.76 198 850139540 0.16 0.99 21.86 777.32 0.01 1.68 0.5 0.14 noise 0 39.81 0.22 -0.49 0.22
951776370 2.33405 110 5.46 -0 2.33 1.05 0.16 2.07 30.49 202 0.58 199 850139544 4.82 0.99 29.99 1170.93 0 2.03 0.5 0.09 noise -8.86 29.17 0.21 -0.4 0.4
951776376 1.21916 160 -1.97 -0.02 1.22 1.28 0.09 1.91 27.86 203 0.39 200 850139510 0.12 0.99 42.03 1364.56 0 1.83 0.11 0.03 noise 2.82 23.92 0.22 -0.18 0.31
951776382 1.59633 140 0.57 -0.01 1.6 0.86 0.14 2.07 38.47 204 0.63 201 850139510 2.25 0.99 50.78 1218.21 0.01 1.35 0.28 0.07 noise -9.4 29.65 0.29 -0.46 0.23
951776388 2.31338 160 4.05 0.01 2.31 1.63 0.3 2.4 21.87 205 0.42 202 850139544 2.61 0.99 31.66 990.06 0 1.55 0.5 0.08 noise 0.71 31.83 0.19 -0.29 0.32
951776394 3.37784 160 -6.63 0.01 3.38 1.39 0.56 0.03 29.31 206 0.67 203 850139544 12.54 0.99 25.84 815 0.47 nan 0.5 0.22 noise 1.91 46.64 0.19 nan 0.14
951776401 0.3811 140 -7.27 0.02 0.38 1.58 0.1 0.03 96.42 207 1.21 204 850139544 1.65 0.99 42.43 1161.56 2.14 0.69 0.21 0 noise 1.24 17.15 0.56 nan 2.67
951776407 1.67166 40 0.41 0.17 1.67 5.44 0.99 1.52 80.05 208 1.88 205 850139546 1.17 0.99 13.27 193.97 0.04 2.27 0.03 0 good nan 51.86 0.03 nan 0.26
951776412 2.13885 10 nan 0.14 2.14 6.19 1 0.44 71.56 209 1.84 206 850139566 0.59 0.99 15.66 154.49 0.22 0.21 0.01 0 good nan 70.73 0.01 -0.03 0.04
951776419 2.17935 170 -6.72 0.02 2.18 1.17 0.36 0.03 27.43 210 0.45 207 850139542 2.94 0.99 26.01 743.09 0.42 nan 0.5 0.07 noise -0.38 32.35 0.32 nan 6.52
951776425 3.04179 110 -0.69 0.04 3.04 2.68 0.81 1.59 35.73 211 0.83 208 850139580 17.51 0.99 41.05 430.28 0.03 nan 0.5 0.15 good -0.54 97.89 0.11 nan 4.38
951776431 25.9364 60 0.34 0.11 25.94 3.64 0.95 0.41 85.6 212 2.48 209 850139594 0.61 0.99 58.48 76.77 0.25 0.25 0 0.05 good 0.21 117.06 0.08 -0.06 0.01
951776436 16.3894 60 -0.34 0.04 16.39 2.92 0.94 0.65 52.95 213 1.63 210 850139594 0.25 0.99 54.26 97.4 0.15 0.18 0.24 0.04 good 0.21 70.58 0.03 -0.01 0.05
951776442 0.89551 170 1.27 -0.02 0.9 nan nan 2.09 32.91 214 0.48 211 850139590 3.1 0.99 79.47 2389.83 0.01 1.62 0.5 0 noise -4.8 nan nan -0.24 18.26
951776449 0.88187 160 0.54 0.06 0.88 1.71 0.14 2.03 37.94 215 0.77 212 850139594 0.48 0.99 37.24 1209.42 0.02 0.95 0.43 0.02 noise -1.27 24.27 0.14 -0.43 11.55
951776455 4.70261 70 -0.14 0.13 4.7 4.96 0.98 0.7 52.38 216 1.36 213 850139600 0.14 0.99 45.78 130.55 0.13 0.44 0.04 0 good 1.03 71.45 0 -0.02 0.08
951776462 2.2024 160 -3.42 0.06 2.2 2.55 0.54 0.84 30.76 217 0.88 214 850139602 0.05 0.99 39.36 432.02 0.05 0.58 0.5 0.01 noise -1.57 37.36 0.04 -0 2.46
951776468 0.30908 160 -0.75 -0.02 0.31 nan nan 2.06 25.59 218 0.89 215 850139604 2.69 0.92 63 445.89 0.04 1.09 0.5 0 noise 2.07 nan nan nan 26.35
951776475 5.13217 50 0.34 0.08 5.13 4.31 0.98 0.62 65.12 219 1.73 216 850139606 0.43 0.99 51.3 79.7 0.2 0.18 0 0 good 1.03 65.51 0.02 -0.03 0.01
951776480 0.34979 100 -1.84 0.15 0.35 4.99 0.96 0.54 83.78 220 3.17 217 850139610 0.39 0.88 25.04 109.75 0.23 0.23 0 0 good -0.69 59.46 0 -0.02 0.63
951776486 11.6435 120 -0.09 0.13 11.65 5.19 1 0.48 55.63 221 2.1 218 850139610 0.46 0.99 47.96 94.16 0.22 0.21 0 0 good 0.87 117.31 0 -0.03 0
951776493 3.33826 170 0.05 0.03 3.34 nan nan 0.89 24.27 222 0.51 219 850139618 0.43 0.99 55.12 1389.34 0.02 nan 0.5 0 noise 2.53 nan nan nan 1.21
951776499 2.7602 170 -0.27 0.06 2.76 2.33 0.6 1.28 26.66 223 0.53 220 850139618 0.45 0.99 14.52 578.75 0.01 1.48 0.5 0.04 noise 0.46 43.83 0.06 -0.02 0.82
951776505 1.7409 140 -3.34 0.13 1.74 4.67 0.96 0.71 58.34 224 1.1 221 850139622 0.34 0.95 28.99 271.1 0.09 1.09 0.01 0 noise -0.64 61.53 0 -0.01 0.43
951776512 3.64651 130 -2.4 0.15 3.65 2.96 0.65 0.71 44.33 225 0.86 222 850139618 0.12 0.96 29.6 447.94 0.05 1.5 0.14 0.02 noise -1.13 40.69 0.06 -0.01 0.79
951776518 1.70142 120 -1.24 0.02 1.7 2.92 0.83 0.4 55.15 226 1.34 223 850139620 1.02 0.99 52.52 265.66 0.12 0.4 0.3 0.01 noise -1.38 37.56 0.06 -0.12 1.22
951776524 0.23643 90 nan 0.05 0.24 4.15 0.65 0.62 93.42 227 2.05 224 850139620 0.57 0.98 23.97 162.02 0.22 0.25 0.07 0 good -0.96 37.16 0.01 -0.02 5.54
951776530 2.69469 170 0.62 0.02 2.7 1.76 0.46 2.02 29.58 228 0.53 225 850139618 0.46 0.99 19.89 714.33 0.02 2.5 0.5 0.04 noise 0.21 42.93 0.07 -0.25 2.95
951776541 2.25727 170 -1.41 0.03 2.26 2.41 0.73 0.47 35.67 229 0.98 226 850139620 4.24 0.97 55.14 272.64 0.07 0.48 0.1 0.02 noise -1.64 41.05 0.06 -0.06 0.97
951776547 2.07664 140 -2.6 0.06 2.08 3.76 0.76 0.62 60.95 230 1.59 227 850139630 0.19 0.81 40.07 197.35 0.2 0.26 0 0.01 noise -0.62 41.43 0.05 -0.02 1.49
951776551 0.64513 130 -1.51 0.03 0.65 3.1 0.42 0.69 57.08 231 1.52 228 850139624 0.37 0.94 19.94 264.34 0.15 0.27 0.07 0.01 good -0.84 27.97 0.09 -0.02 5.4
951776556 3.84606 170 -2.08 0.05 3.85 1.86 0.41 1.63 28.55 232 0.52 229 850139618 0.38 0.99 26.92 525.1 0.03 nan 0.5 0.02 noise -1.35 35.45 0.06 nan 1.26
951776563 2.90591 130 -2.51 0.11 2.91 2.54 0.69 1.24 73.26 233 1.37 230 850139642 3.39 0.99 39.15 222.12 0.02 nan 0.02 0.01 good 0.67 37.38 0.04 nan 0.28
951776569 4.88251 130 -3.3 0.03 4.88 2.08 0.71 0.78 48.06 234 1.41 231 850139630 0.18 0.99 21.76 372.74 0.11 0.33 0.14 0.04 good -0.57 44.02 0.06 -0.01 0.61
951776576 0.00723 100 -1.37 nan 0.01 5.91 0 0.14 164.52 235 2.82 232 850139632 1.16 0.3 nan 0 0.45 0.19 0 0 good -0.25 90.81 0 -0.49 0
951776582 0.00858 170 -2.19 nan 0.01 1.99 0 0.81 94.52 236 0.83 233 850139630 0.52 0.45 nan 0 0.29 0.32 0.5 0 noise -2.22 19.55 0.03 -0.01 0
951776589 1.49506 110 -2.2 0.23 1.5 3.33 0.89 0.73 116.72 237 2.42 234 850139632 0.97 0.99 60.64 291.45 0.3 0.21 0.01 0 good -0.08 40.22 0.04 -0.02 0.5
951776595 0.3068 110 -2.13 0.12 0.31 4.55 0.75 0.62 145.36 238 2.92 235 850139632 0.7 0.96 23.8 57.95 0.48 0.15 0 0 good -0.1 40.55 0.01 -0.02 0.41
951776599 1.85973 150 -0.02 0.03 1.86 nan nan 2.1 65.12 239 0.72 236 850139652 2.9 0.99 62.22 1821.2 0.05 1.28 0.45 0 noise -0.27 nan nan -1.02 5.41
951776606 0.05828 160 0 nan 0.06 nan nan 2.29 283.2 240 2.36 237 850139652 2.4 0.81 84.39 72.44 0.07 1.19 0.04 0 noise -7.38 nan nan -5.83 0
951776612 0.34556 150 -1.58 0.02 0.35 2.74 0.3 0.03 176.81 241 1 238 850139652 1.22 0.99 42.77 377.81 3.74 1.33 0.09 0 noise 0.32 15.22 0.32 nan 125.5
951776618 2.53968 120 -1.55 0.17 2.54 2.46 0.69 0.54 64.25 242 1.76 239 850139638 0.36 0.99 80.65 316.16 0.22 0.22 0.03 0 good -0.54 36.01 0.04 -0.01 0.61
951776624 9.47982 70 -1.44 0.11 9.48 2.55 0.88 0.99 51.85 243 1.5 240 850139638 0.3 0.99 33.83 151.28 0.12 0.27 0.17 0.01 good 1.44 57.17 0.02 -0.01 0.06
951776630 3.25229 60 -1.79 0.1 3.25 2.37 0.82 0.89 92.3 244 2.19 241 850139638 0.2 0.99 45.6 104.01 0.3 0.19 0 0 good 0.69 36.83 0.05 -0.02 0.07
951776636 3.49523 140 -2.29 0.09 3.5 2.26 0.63 1.33 68.59 245 1.26 242 850139642 4.31 0.98 54.21 294.62 0.02 nan 0.04 0.01 good 0.91 36.49 0.05 nan 1.07
951776642 1.51511 170 -0.29 0.07 1.52 2.76 0.87 1.09 39.35 246 0.42 243 850139642 6.19 0.99 25.85 519.45 0 1.88 0.5 0 noise -0.82 43.42 0.02 nan 6.26
951776647 3.67679 140 -1.75 0.06 3.68 1.78 0.66 1.41 58.29 247 1 244 850139642 4.03 0.99 73.4 315.29 0.02 nan 0.13 0.01 noise 0.17 36.42 0.05 nan 0.44
951776653 5.73586 120 -1.64 0.05 5.74 2.42 0.61 0.77 90.01 248 1.08 245 850139654 0.29 0.99 57.29 317.49 0.25 0.3 0.16 0.02 noise 1.03 34.81 0.06 -0.03 0.77
951776660 2.62494 110 -1.51 0.06 2.63 2.53 0.67 1.28 115.66 249 1.78 246 850139642 1.06 0.99 26.38 272.69 0.02 nan 0.03 0 good 0.67 33.06 0.06 nan 0.57
951776666 1.85581 80 -1.1 0.13 1.86 3.91 0.89 0.74 132.87 250 2 247 850139642 0.81 0.99 52.79 204.75 0.42 0.14 0 0 good -0.21 41.83 0.01 -0.02 0.56
951776671 7.42644 80 -1.79 0.08 7.43 2.63 0.87 0.96 76.16 251 1.27 248 850139642 0.91 0.96 41.82 116.54 0.18 0.16 0.04 0.02 good 1.37 53.34 0.02 -0 0.21
951776677 0.02563 70 -0.48 nan 0.03 5.06 0 0.73 245.54 252 2.84 249 850139642 0.42 0.77 6.87 0 0.8 0.14 0.12 0 good -0.27 32.76 0 -0.03 0
951776683 1.38026 80 -0.82 0.08 1.38 3.53 0.72 0.84 149.73 253 2.58 250 850139648 0.33 0.43 23.47 160.87 0.49 0.15 0 0 good 0.41 47.73 0.01 -0.03 1.38
951776690 0.38668 80 -1.3 0.2 0.39 6 0.84 0.69 264.77 254 3.49 251 850139644 0.43 0.95 26.6 158.87 0.87 0.16 0 0 good -0.41 46.53 0 -0.05 2.85
951776697 3.73518 70 -0.76 0.05 3.74 4.27 0.95 0.74 233.48 255 3.51 252 850139644 0.34 0.85 34.51 122.75 0.76 0.16 0 0 good -0.34 68.5 0 -0.03 0.35
951776703 5.1762 90 -0.62 0.05 5.18 1.93 0.57 0.76 90.6 256 0.9 253 850139652 0.72 0.99 64.07 271.01 0.14 0.22 0.31 0.01 good 0.69 34.95 0.06 -0.02 0.55
951776710 0.80106 80 -0.69 0.1 0.8 4.55 0.83 0.82 207.28 257 3.21 254 850139648 0.31 0.97 9.16 82.55 0.6 0.18 0.01 0 good 0.53 57.23 0 -0.04 1.63
951776716 4.67522 80 0 0.04 4.68 1.75 0.73 0.59 97.13 258 1.64 255 850139648 0.31 0.99 75.1 229.48 0.37 0.15 0.02 0.01 good -0.22 44.06 0.02 -0.01 0.36
951776723 2.30098 50 -2.06 0.12 2.3 2.85 0.94 0.76 113.84 259 1.48 256 850139650 0.52 0.6 25.85 110.23 0.41 nan 0.05 0 good 0.69 63.23 0 -0.02 0.13
951776731 0.20771 60 -0.69 nan 0.21 5.14 0.61 0.78 281.48 260 4.04 257 850139648 0.23 0.52 8.85 57.97 1.01 0.14 0.01 0 good 0.96 50.93 0 -0.02 0
951776737 10.9451 60 0.21 0.15 10.95 4.94 1 0.37 284.59 261 1.31 258 850139652 0.38 0.99 73.65 234.69 0.3 0.12 0 0 good 0 106.55 0 -0.05 0.06
951776743 11.8429 30 nan 0.13 11.85 8.3 1 0.19 465.45 262 5.09 259 850139650 0.07 0.56 24.56 44.43 1.71 0.21 0 0 good 0 214.15 0 -0.53 0.01
951776748 1.14434 60 -1.72 0.1 1.14 2.7 0.66 0.52 118.79 263 1.69 260 850139654 0.13 0.58 38.74 119.28 0.44 0.21 0.01 0 good -0.14 40.45 0.01 -0.01 0.35
951776753 5.10355 50 0 0.12 5.1 3.23 0.89 0.66 265.23 264 3.76 261 850139652 0.24 0.99 65.62 112.37 0.94 0.16 0 0 good 0.07 48.31 0.01 -0.04 0.52
951776760 6.08576 60 -0.34 0.1 6.09 2.7 0.92 0.67 157.46 265 2.47 262 850139652 0.37 0.99 74.42 146.31 0.51 0.15 0.01 0 good -0.21 53.34 0.01 -0.02 0.67
951776767 16.1401 50 0 0.06 16.14 3.13 0.98 0.65 146 266 2.15 263 850139652 0.31 0.99 66.57 112.51 0.43 0.21 0 0.01 good -0.21 79.3 0 -0.02 0.02
951776772 2.8405 50 -1.37 0.15 2.84 3.1 0.78 0.95 295.47 267 3.34 264 850139652 0.25 0.98 37.13 121.79 1.07 0.16 0.01 0 good -0.34 40.05 0.02 -0.02 1.47
951776776 3.27616 90 -0.47 -0.01 3.28 2.34 0.81 0.85 134.63 268 1.51 265 850139652 0.36 0.99 51.61 288.33 0.33 0.19 0.02 0 good 0.48 45.03 0.02 -0.01 0.52
951776781 5.68213 40 0 0.12 5.68 3.03 0.9 1.25 186.94 269 2.4 266 850139652 0.21 0.99 58.79 133.53 0.79 0.22 0.03 0 noise -0.34 60.99 0.01 -0.03 0.34
951776789 4.30807 60 -0.34 0.1 4.31 1.96 0.84 0.87 123.83 270 1.84 267 850139652 0.27 0.99 60.51 134.37 0.45 0.14 0.02 0 good 0.21 48.19 0.01 -0.04 0.41
951776794 1.27733 70 -1.51 0.13 1.28 4.72 0.94 0.78 213.13 271 1.98 268 850139650 0.42 0.86 13.99 124.92 0.57 1.13 0.03 0 good 0.96 55.6 0 -0.02 5.72
951776799 4.62221 50 -0.41 0.08 4.62 2.38 0.84 0.89 138.58 272 0.79 269 850139656 0.15 0.99 59.33 219.87 0.12 0.44 0.08 0 good 0 49.99 0.01 -0.01 0.9
951776806 3.71358 70 -0.34 0.08 3.71 3.73 0.98 0.48 96.37 273 1.18 270 850139652 0.54 0.99 53.41 138.88 0.33 0.15 0 0 good -0.14 68.98 0 -0.04 0.03
951776812 4.75965 70 -0.76 0.07 4.76 2.26 0.81 0.87 74.65 274 1.49 271 850139658 0.74 0.99 67.37 224.92 0.2 0.23 0.33 0.01 good 1.37 49.65 0.01 -0.01 0.35
951776818 5.79559 70 -0.34 0.1 5.8 4.29 0.98 0.93 95.39 275 1.82 272 850139658 0.5 0.98 44.75 85.4 0.32 0.15 0 0 good -0.19 76 0 -0.02 0.05
951776824 1.50478 60 -0.48 0.12 1.51 3.39 0.76 0.99 185.28 276 2.49 273 850139660 0.06 0.99 51.14 128.84 0.62 0.14 0.01 0 good -0.34 42.02 0.01 -0.02 0.51
951776832 4.22158 80 -0.65 0.03 4.22 2.62 0.78 1 92.03 277 0.6 274 850139660 0.27 0.99 47.37 439.8 0.09 0.4 0.41 0 good 2.06 46.57 0.01 -0.01 0.84
951776838 8.0572 70 -0.76 0.07 8.06 3.49 0.99 1.06 144.81 278 1.93 275 850139660 0.05 0.99 55.27 70.91 0.45 0.16 0 0 good -0.21 61.53 0.01 -0.01 0.01
951776845 0.01095 170 0.11 nan 0.01 3.73 nan 1.25 138.81 279 0.75 276 850139652 1.22 0.51 nan 0 0.02 1.84 0.33 0 noise 0.46 18.53 0.02 nan 322.75
951776852 2.96067 100 -1.31 0.05 2.96 3.24 0.83 1.25 69.02 280 1.31 277 850139662 2.16 0.99 31.18 236.8 0.01 nan 0.37 0 good 1.03 49.31 0.01 nan 0.54
951776857 0.6226 70 -2.88 -0.05 0.62 3.73 0.55 1.36 74.06 281 1.2 278 850139662 2.44 0.85 18.78 302.73 0.01 nan 0.47 0 good 0 30.18 0.02 nan 3.9
951776864 3.84451 90 -1.17 0.04 3.85 5.08 0.94 1.25 87.42 282 1.8 279 850139662 1.09 0.99 43.73 105.98 0.02 nan 0.03 0 good 0.76 73.52 0 nan 0.1
951776869 27.6137 90 -0.34 0.05 27.62 2.75 0.97 1.77 104.72 283 1.98 280 850139658 1.26 0.99 55.79 98.23 0.14 0.3 0 0.05 good 0.12 90.63 0.02 nan 0.01
951776877 4.8419 100 -0.02 0.05 4.84 1.89 0.52 0.88 78.15 284 1.24 281 850139664 0.19 0.99 46.4 345.45 0.25 0.3 0.07 0.01 good 0.76 31.21 0.11 -0.02 0.37
951776884 1.78947 70 -0.76 0.09 1.79 2.54 0.84 1.06 91.3 285 1.21 282 850139664 0.13 0.99 45.83 138.65 0.16 0.33 0.03 0 good -0.34 44.63 0.02 -0.01 0.46
951776888 4.99505 110 -0.21 0.07 5 2.96 0.93 0.4 61.77 286 0.78 283 850139660 0.19 0.99 36.71 290.96 0.21 0.15 0.5 0.01 good 0.12 55.46 0.01 -0.06 0.27
951776896 7.33798 80 -0.49 0.08 7.34 3.64 0.99 0.87 66.14 287 1.7 284 850139668 0.04 0.99 51.91 125.84 0.19 0.29 0 0 good 0 68.95 0 -0 0.05
951776902 1.86769 140 1.59 0.05 1.87 2.85 0.42 1.55 41.42 288 1.12 285 850139676 1.01 0.99 27.95 309.3 0.01 1.61 0.5 0.01 noise 0.29 30.46 0.1 nan 5.68
951776909 4.72844 100 0 0.05 4.73 2.67 0.61 1.68 61.42 289 1.48 286 850139678 1.1 0.99 18.85 204.2 0.03 0.8 0.5 0.03 noise 0.07 38.99 0.08 nan 0.49
951776914 1.52307 150 -6.03 0.03 1.52 nan nan 1.09 43.55 290 0.94 287 850139678 2.47 0.99 65.86 2259.43 0.05 1.52 0.5 0 noise -0.32 nan nan nan 0.67
951776922 7.57958 40 0.34 0.09 7.58 4.14 0.88 0.41 83.05 291 2.23 288 850139678 0.6 0.99 22.58 176.64 0.31 0.16 0.5 0.02 good 2.06 66.33 0.01 -0.02 0.13
951776927 2.80154 160 2.01 0.02 2.8 1.89 0.43 0.93 52.75 292 1.09 289 850139678 1.69 0.99 30.8 481.02 0.05 1.26 0.5 0.03 good -0.31 36.63 0.12 nan 5.59
951776932 1.71186 170 -0.31 0.04 1.71 3.7 0.9 1.43 31.94 293 0.6 290 850139678 55.62 0.99 123.82 2543.23 0 1.02 0.5 0 noise 0.23 49.13 0 -0.03 11.05
951776939 8.60229 110 -5.97 0.08 8.6 2.27 0.76 1.7 39.25 294 1.26 291 850139684 1.23 0.89 16.83 165.41 0.03 0.76 0.22 0.08 good 0.34 56.78 0.09 nan 0.11
951776944 12.1399 50 2.2 0.09 12.14 4.26 0.88 0.19 57.45 295 1.72 292 850139688 1.15 0.64 18.58 60.82 0.25 0.33 0.01 0.03 good 0 107.57 0.04 -0.2 0.01
951776950 0.62704 70 2.1 0.01 0.63 4.59 0.64 0.69 48.58 296 0.63 293 850139700 0.74 0.55 40.14 575.8 0.01 nan 0.5 0 good -0.5 50.96 0.01 -0.09 0.59
951776956 0.55915 170 -0.19 0.04 0.56 4.12 0.66 1.02 19.19 297 0.1 294 850139700 0.91 0.99 135.34 1665.09 0 nan 0.5 0 noise -0.33 42.63 0.01 -0.01 3.72
951776962 1.88547 10 nan 0.05 1.89 5.01 0.9 1.66 69.08 298 0.96 295 850139700 0.73 0.59 92.45 758.47 0.09 nan 0.2 0.01 noise nan 75.88 0.01 nan 0.02
951776968 0.07606 60 -1.95 nan 0.08 5.03 0.84 0.85 51.03 299 0.58 296 850139700 0.71 0.49 23.97 78.79 0.03 nan 0.43 0 noise 0.04 42.91 0 -0.03 6.69
951776973 5.24429 60 -0.69 0.11 5.25 2.67 0.88 0.84 46.99 300 1.96 297 850139710 0.06 0.99 46.12 145.12 0.11 0.3 0.07 0.02 good 0.48 59.28 0.03 -0 0.12
951776980 0.49395 170 0.01 0.06 0.49 3.49 0.63 0.63 28.95 301 0.61 298 850139776 0.4 0.98 34.37 482.65 0.03 1.14 0.19 0 noise -0.07 46.59 0.01 -0.02 2.22
951776985 2.14122 60 -0.69 0.09 2.14 3.03 0.84 0.76 65.24 302 2.47 299 850139714 0.28 0.99 57.96 221.1 0.19 0.29 0.02 0 good 0.27 42.18 0.05 -0.01 0.11
951776991 1.7595 70 -0.34 0.01 1.76 4.08 0.97 0.95 52.28 303 1.85 300 850139716 0.26 0.99 61.64 297.14 0.13 0.25 0.13 0 good 0.89 58.47 0.01 -0.02 0.23
951776998 15.5874 60 0 0.1 15.59 4.24 0.98 0.34 85.73 304 2.56 301 850139718 0.68 0.99 67.75 97.94 0.34 0.16 0 0.03 good -0.07 97.5 0.01 -0.07 0.01
951777003 0.02139 50 -0.34 nan 0.02 4.36 0 0.69 76.52 305 2.55 302 850139720 0.12 0.62 nan 0 0.26 0.21 0.5 0 good 0.69 35.38 0 -0.03 0
951777009 2.26564 110 0.96 0.15 2.27 3.86 0.9 1.22 46.05 306 1.06 303 850139728 2.41 0.99 58.64 271.58 0.03 nan 0.03 0 good 2.31 46.66 0.03 -0.01 0.11
951777016 7.24705 110 -1.33 0.12 7.25 4.01 0.97 0.45 45.77 307 1.93 304 850139724 0.33 0.99 53.24 167.31 0.13 0.29 0.08 0.01 good 0.49 74.62 0.01 -0.01 0.02
951777021 6.45084 90 -0.76 0.1 6.45 4.23 0.97 0.29 45.09 308 2 305 850139730 0.9 0.99 50.18 209.87 0.2 0.16 0.22 0.01 good 0.21 73.02 0 -0.04 0.09
951777029 2.72641 80 0.69 0.07 2.73 4.21 0.87 0.7 40.66 309 1.64 306 850139724 0.34 0.99 48.92 324.42 0.1 0.26 0.29 0 good 1.04 49.36 0.02 -0.02 0.07
951777034 0.00124 160 -3.79 nan 0 5.39 nan 0.55 107.85 310 3.4 307 850139732 0.49 0.09 nan 0 0.35 0.19 0.02 0 noise 2.27 4.70247e+13 nan 0 0
951777040 1.73635 60 -1.03 0.08 1.74 2.14 0.55 0.29 57.98 311 1.85 308 850139732 0.8 0.99 60.12 234.91 0.23 0.19 0.1 0.01 noise 0 35.1 0.1 -0.04 0.86
951777046 3.54597 110 0.49 0.14 3.55 3.97 0.88 0.63 47.11 312 1.64 309 850139736 0.15 0.99 53.29 202.05 0.12 0.41 0.01 0.01 good 2.63 57.55 0.01 -0.02 0.05
951777052 13.0328 90 -0.69 0.07 13.04 3.73 0.94 0.29 57.59 313 1.83 310 850139736 0.01 0.99 51.71 150.8 0.25 0.33 0.02 0.03 good -0.14 71.39 0.02 -0.06 0.1
951777058 0.75921 100 -0.02 0.11 0.76 3.78 0.92 0.56 47.95 314 0.6 311 850139742 0.45 0.99 33.2 266.61 0.12 1.1 0.06 0 good 2.81 49.06 0.01 -0.02 0.6
951777065 1.94437 110 -0.35 0.09 1.94 2.54 0.52 0.38 46.67 315 0.59 312 850139742 0.38 0.99 25.62 398.68 0.18 0.87 0.5 0.01 good -0.27 33.97 0.09 -0.04 0.99
951777071 1.55035 120 0.26 0.06 1.55 2.49 0.56 1.28 38.82 316 1.23 313 850139744 1.55 0.99 61.27 660.77 0.01 0.93 0.5 0.01 good 1.3 39.69 0.04 nan 0.34
951777079 2.82437 70 -0.21 0.12 2.82 2.83 0.79 0.71 56.48 317 2.16 314 850139746 0.12 0.99 40.38 163.18 0.17 0.26 0.03 0 good 0.21 43.2 0.04 -0.02 0.16
951777092 4.38795 60 0.69 0.1 4.39 6.45 0.98 0.69 82.74 318 1 315 850139742 0.2 0.99 42.92 109.15 0.26 0.36 0 0 good 1.92 84.07 0 -0.03 0
951777098 16.4999 100 -0.48 0.13 16.5 4.15 0.98 0.3 50.96 319 2.19 316 850139750 0.82 0.99 37.76 105.7 0.22 0.18 0.19 0.02 good 0.1 103.43 0 -0.04 0.05
951777105 1.70287 80 -0.07 0.11 1.7 2.19 0.68 0.66 54.19 320 0.7 317 850139758 0.28 0.99 55.64 273.46 0.15 0.93 0.18 0 good 0.89 41.35 0.02 -0.02 0.23
951777112 6.41085 70 0.48 0.19 6.41 4.1 0.97 0.66 149.78 321 3.4 318 850139762 0.86 0.99 47.84 95.86 0.39 0.18 0 0 good 0.96 64.02 0.01 -0.07 0
951777117 4.244 100 0.49 0.12 4.24 2.73 0.84 1.41 52.7 322 1.28 319 850139764 1.02 0.99 45.29 269.19 0.02 0.77 0.12 0.01 good 1.44 52.59 0.01 nan 0.09
951777123 7.17006 70 0.26 0.12 7.17 3.26 0.8 0.66 70.69 323 2.15 320 850139764 0.98 0.99 37.19 237.85 0.15 0.23 0.37 0.01 good 1.42 60.58 0.01 -0.03 0.22
951777129 12.4829 60 0 0.06 12.49 4.17 0.98 0.69 109.63 324 3.28 321 850139764 0.67 0.99 50.47 87.14 0.26 0.21 0 0 good 1.3 73.49 0.01 -0.05 0.01
951777136 9.09128 120 0.41 0.14 9.09 2.02 0.87 1.28 82.78 325 2.05 322 850139762 1.22 0.99 47.1 124.7 0.04 0.88 0.01 0.01 good 2.05 60.78 0.02 0 0.06
951777142 10.2364 90 0.69 0.15 10.24 4.36 1 0.69 176.85 326 4.68 323 850139766 0.33 0.99 42.72 93.83 0.53 0.19 0 0 good 1.84 74.04 0 -0.08 0
951777148 5.99234 60 0 0.12 5.99 4.23 0.97 0.63 124.28 327 3.62 324 850139766 0.3 0.99 44.76 69.9 0.35 0.23 0 0 good 1.42 72.58 0 -0.06 0.02
951777155 4.41244 130 0.55 0.09 4.41 2.66 0.78 0.69 58.74 328 1.71 325 850139766 0.32 0.99 56.74 314.99 0.13 0.38 0.32 0.01 good 1.17 52.85 0.01 -0.04 0.19
951777162 5.94036 70 0.69 0.12 5.94 2.83 0.96 0.66 121.4 329 2.86 326 850139772 0.19 0.99 52.43 114.18 0.32 0.25 0 0 good 0.76 53.99 0.01 -0.06 0.02
951777168 8.81382 60 -1.72 0.11 8.82 2.71 0.71 0.66 65.86 330 1.76 327 850139772 0.07 0.99 47.69 154.37 0.14 0.43 0.29 0.02 good 0.34 48.23 0.04 -0.03 0.14
951777175 4.78135 110 0.45 0.07 4.78 1.95 0.73 1.29 58.5 331 1.22 328 850139778 12.61 0.99 68.21 229.67 0.03 nan 0.05 0.01 good 2.12 43.26 0.03 nan 0.22
951777181 6.2388 120 0.56 0.06 6.24 1.87 0.54 1.29 54.39 332 1.13 329 850139778 59.29 0.99 78.4 259.93 0.03 nan 0.47 0.02 good 1.18 38.95 0.07 nan 0.23
951777188 9.04302 70 -0.34 0.04 9.04 2.41 0.79 0.74 56.23 333 1.55 330 850139772 0.11 0.99 51.74 164.02 0.12 0.49 0.19 0.04 good 0.41 54.85 0.03 -0.01 0.06
951777193 0.42626 170 -0.57 -0.02 0.43 4.97 0.85 0.62 41.1 334 0.84 331 850139776 0.18 0.97 78.38 818.44 0.04 0.41 0.5 0 noise -0.08 43.92 0 -0.03 19.18
951777199 6.21296 110 0.35 0.09 6.21 4.25 0.88 1.41 114.03 335 2.45 332 850139778 1.66 0.99 55.34 129.58 0.04 2.13 0 0.01 good 1.71 52.36 0.02 -0.02 0.08
951777205 2.5617 60 0.48 0.06 2.56 2.61 0.77 0.73 70.39 336 1.68 333 850139780 0.35 0.99 38.86 164.66 0.2 0.98 0.01 0 good 0.69 42.56 0.02 -0.03 0.04
951777212 8.14979 90 -0.34 0.09 8.15 2.25 0.65 1.36 70.66 337 1.29 334 850139778 10.8 0.99 50.36 217.53 0.02 nan 0.17 0.05 good 1.3 48.51 0.06 -0.03 0.12
951777218 8.29714 90 -0.41 0.03 8.3 2.88 0.72 0.76 52.55 338 0.82 335 850139782 0.66 0.99 42.4 195.13 0.11 nan 0.27 0.05 good 2.42 57.7 0.04 -0.02 0.2
951777223 4.54461 100 0.27 0.08 4.55 2.9 0.79 0.85 51.22 339 1.81 336 850139786 0.06 0.99 49.57 334.5 0.12 0.37 0.17 0.01 good 1.55 45.47 0.06 -0.01 0.31
951777227 5.30526 30 nan 0.16 5.31 4.53 0.96 0.91 97.2 340 3.03 337 850139790 0.08 0.99 17.1 138.73 0.32 0.22 0.03 0 noise 1.37 62.74 0.01 -0.02 0.02
951777232 4.30135 70 -2.06 0.1 4.3 2.63 0.87 0.74 66.76 341 2.17 338 850139790 0.13 0.99 38.27 239.79 0.17 0.41 0.13 0.01 good 0.96 48.31 0.04 -0.01 0.32
951777237 1.81179 60 -1.37 0.03 1.81 3.8 0.85 0.4 74.51 342 2.32 339 850139790 0.02 0.99 45.58 208.22 0.28 0.33 0.02 0 good 1.1 50.86 0.02 -0.06 0.11
951777243 0.69834 70 -0.21 0.09 0.7 3.92 0.85 1.35 68.01 343 2 340 850139796 7.76 0.99 23.36 444.84 0.03 nan 0.2 0 good 1.47 49.3 0.01 -0 0.32
951777249 3.40781 50 -0.69 0.15 3.41 3.83 0.98 0.47 112.58 344 3.35 341 850139798 0.56 0.99 56.49 101.93 0.37 0.21 0 0 good 0.34 59.98 0.01 -0.08 0
951777257 1.51222 70 -0.41 0.1 1.51 2.83 0.87 0.73 46.65 345 1.7 342 850139806 0.53 0.99 36.38 426.32 0.12 0.22 0.46 0 good 3.43 47.52 0.03 -0.01 0.25
951777263 3.24774 80 -1.24 0.09 3.25 3.24 0.85 1.69 52.95 346 1.92 343 850139806 1.38 0.99 44.12 262.35 0.05 0.54 0.45 0.01 good -0.55 62.1 0.02 nan 1.04
951777270 1.99283 100 1.77 0.07 1.99 1.84 0.68 0.71 45.24 347 1.64 344 850139806 0.7 0.99 41.1 460.14 0.13 0.18 0.34 0.03 good 2.95 44.91 0.05 -0.01 0.36
951777275 1.71165 170 0.02 0 1.71 nan nan 1.06 23.12 348 0.85 345 850139808 0.22 0.99 117.11 2226.3 0.02 nan 0.5 0 noise 0.21 nan nan nan 1.08
951777281 2.62432 100 2.62 0.08 2.62 2.29 0.66 0.62 38.92 349 1.41 346 850139808 0.14 0.99 25.16 357.08 0.11 0.51 0.5 0.04 good 3.71 44.99 0.07 -0.01 1.18
951777287 3.70531 110 0.94 0.05 3.71 3.14 0.82 1.06 30.19 350 1.06 347 850139812 0.35 0.99 94.34 417.41 0.05 1.17 0.26 0.01 good 3.78 62.83 0.03 -0.01 0.36
951777292 6.32219 20 nan 0.08 6.32 4.73 0.98 0.32 72.67 351 2.46 348 850139812 0.02 0.99 39.59 170.93 0.31 0.21 0.01 0.01 good 0 85.27 0.01 -0.05 0.06
951777298 2.21759 50 0.48 0.08 2.22 4.38 0.8 0.78 62.79 352 2.7 349 850139814 0.28 0.99 21.8 203.12 0.16 0.26 0.09 0.01 good 2.75 64.09 0.02 -0.01 0.72
951777304 2.35492 70 0.82 0.03 2.36 2.09 0.72 0.52 41.23 353 1.36 350 850139816 0.1 0.99 40.51 280.42 0.14 0.41 0.5 0.04 good 2.06 43.61 0.08 -0.01 0.82
951777310 0.00692 80 -2.03 nan 0.01 3.27 0 0.95 82.86 354 2.5 351 850139820 0.09 0.25 nan 0 0.24 0.26 0.5 0 noise 13.05 46.76 0 -0.03 0
951777315 0.85717 70 0.21 0.03 0.86 4.12 0.95 0.73 39.24 355 1.35 352 850139826 0.03 0.96 33.11 425.75 0.06 0.47 0.5 0.01 good 1.1 56.05 0.04 -0.01 1
951777321 5.74124 100 0.32 0.09 5.74 nan nan 1.04 28.71 356 1.01 353 850139864 0.24 0.99 46.04 812.5 0.02 nan 0.5 0 noise 0.69 nan nan -0.03 1.46
951777323 1.19601 90 0.17 0.24 1.2 1.84 0.66 0.6 50.38 357 1.58 354 850139868 0.24 0.97 31.88 390.47 0.07 0.65 0.01 0.04 noise nan 22.54 0.44 -0.03 14.46
951777326 7.5492 90 0.13 0.13 7.55 2.36 0.97 0.74 25.19 358 0.96 355 850139868 0.12 0.99 23.78 550.39 0.03 0.93 0.29 0.34 noise nan 564.87 0.12 -0.01 2.43
951777329 3.32462 30 nan 0.02 3.33 2.85 0.73 0.58 103.01 359 2.22 356 850139168 0.35 0.99 20.86 449.86 0.33 0.3 0.04 0.01 good 0 32.78 0.01 -0.03 0.32
951777333 2.34583 40 nan 0.04 2.35 3.24 0.84 0.65 66.83 360 1.05 357 850139170 0.53 0.99 31.64 600.84 0.17 nan 0.1 0 good 0.89 46.95 0 -0.04 0.1
951777335 8.80669 80 -0.69 0.01 8.81 4.17 0.86 0.55 117.52 361 2.85 358 850139196 0.41 0.99 17.19 69.21 0.35 0.22 0 0.01 good 0.55 77.42 0.01 -0.05 0.07
951777339 6.94045 60 -1.03 0.01 6.94 2.96 0.95 0.59 124.66 362 2.25 359 850139204 0.77 0.99 14.89 131.14 0.37 0.16 0 0 good 0.82 71.9 0 -0.06 0.05
951777342 9.22283 90 -0.55 0.04 9.22 3.74 0.96 0.62 74.45 363 2.36 360 850139212 0.24 0.99 20.43 150.67 0.19 0.27 0.01 0.01 good 0.14 77.48 0 -0.04 0.03
951777345 3.64734 70 -0.27 -0.01 3.65 2.9 0.94 1.35 65.12 364 1.85 361 850139222 1.78 0.99 27.09 147.93 0.01 nan 0 0 good 2.4 66.45 0 -0.02 0.08
951777348 5.85966 80 -0.21 0.1 5.86 3.37 0.99 1.43 66.47 365 2.08 362 850139226 2.02 0.99 18.51 144 0.02 1.62 0.18 0 good 0.34 98.16 0 -0.09 0.01
951777351 2.74057 70 0.07 0.11 2.74 4.86 0.97 1.48 86.74 366 1.98 363 850139230 1.39 0.99 13.4 207.93 0.03 nan 0.08 0 good 0.34 78.12 0 nan 0.12
951777355 0.02976 80 -0.22 nan 0.03 2.9 0.17 1.3 73.11 367 1.2 364 850139240 1.03 0.82 nan 0 0.03 0.71 0.4 0 good 0 42.33 0 -0.01 0
951777360 3.54401 60 -0.62 0.04 3.54 6.19 0.97 1.37 106.25 368 3.16 365 850139262 1.04 0.99 21.07 141.11 0.05 0.78 0 0 good -0.34 86.02 0 -0.1 0.02
951777366 2.21697 50 -0.76 0.04 2.22 3.71 0.7 0.69 80.37 369 2.73 366 850139280 0.95 0.99 18.29 215.35 0.24 0.14 0.05 0.01 good 1.37 50.02 0.01 -0.03 0.04
951777371 2.06393 60 -0.96 0.1 2.06 3.85 0.91 1.28 78.02 370 2.07 367 850139286 1.15 0.99 21.71 252.71 0.03 1.72 0.05 0 good 0.69 62.86 0 -0.01 0.67
951777377 0.0216 100 -0.84 -0.16 0.02 2.91 0 0.63 62.98 371 1.88 368 850139294 0.08 0.65 nan 0 0.16 0.34 0.26 0 good 0.62 30.25 0 -0.03 0
951777384 1.97764 80 -0.21 0.09 1.98 2.69 0.98 1.3 51.25 372 1.49 369 850139300 5.42 0.99 21.07 340.47 0.02 nan 0.04 0 good 2.2 68.4 0 -0.01 0.14
951777389 4.77825 70 -0.69 0.07 4.78 3.49 0.96 0.62 89.61 373 3.06 370 850139306 0.42 0.99 18.57 95.35 0.26 0.19 0.01 0 good -0.69 74.19 0 -0.05 0.05
951777395 2.48264 50 -0.69 -0.03 2.48 3.5 0.97 1.43 89.8 374 2.55 371 850139308 1.4 0.99 25.68 217.23 0.05 1.33 0 0 good -1.37 68.32 0 -0.08 0.14
951777401 0.57599 70 -1.65 0.14 0.58 3.17 0.67 0.55 126.92 375 4.51 372 850139316 0.27 0.98 9.51 40.31 0.46 0.18 0.01 0 good 2.06 33.45 0.02 -0.03 0.12
951777406 9.18087 70 0 0.08 9.18 4.07 0.95 1.4 85.77 376 2.71 373 850139324 1.37 0.99 15.48 101.01 0.04 1.4 0.02 0.01 good 0.69 81.24 0.01 -0.02 0.09
951777413 0.03513 130 -1.71 nan 0.04 1.97 0 1.22 47.03 377 1.36 374 850139338 2.04 0.83 19.66 0 0.02 0.85 0.5 0 good 0.19 32.72 0.01 -0.01 0
951777419 3.67266 70 -1.03 0.06 3.67 3 0.82 1.28 73.51 378 2.26 375 850139340 1.52 0.99 31.08 175.64 0.02 2.27 0.49 0.01 good 0.34 56.12 0.01 -0.01 0.07
951777424 1.44453 80 -0.41 0.03 1.44 1.92 0.52 1.36 59.07 379 1.82 376 850139340 3.5 0.99 35.72 393.75 0.03 1.1 0.2 0.01 good 0.41 48.31 0.01 -0.04 0.09
951777430 3.33051 60 -0.14 -0.01 3.33 3.63 0.77 0.67 72.85 380 2.9 377 850139348 0.59 0.99 9.38 231.97 0.19 0.23 0.46 0.01 good 0.69 53.25 0.01 -0.04 0.19
951777437 0.24656 80 -0.55 0.03 0.25 2.82 0.14 0.63 63.93 381 1.66 378 850139350 0.06 0.94 37.07 197.82 0.12 0.45 0.18 0 good 1.03 31.99 0.02 -0.01 0.64
951777442 0.98799 60 -0.34 -0 0.99 5.09 0.89 1.39 87.26 382 2.01 379 850139368 1.36 0.99 20.77 269.42 0.03 1.65 0 0 good 2.13 44.14 0.02 -0.08 0.08
951777448 1.35814 10 nan 0.06 1.36 3.22 0.83 0.27 106.37 383 3.18 380 850139388 0.77 0.99 36.55 605.48 0.45 0.1 0.05 0 good nan 53.11 0.01 -0.08 0.04
951777455 0.37707 40 0.34 -0.15 0.38 6.5 0.97 0.47 75.54 384 2.6 381 850139390 0.71 0.99 24.43 559.54 0.27 0.18 0.5 0 good 2.06 76.05 0 -0.06 9.26
951777462 0.18022 110 -0.34 -0.12 0.18 3.06 0.43 1.61 38.47 385 0.71 382 850139488 1.79 0.99 34.29 222.13 0.02 1.68 0.25 0 good 0.66 31.08 0.11 nan 27.42
951777468 0.05012 50 -1.37 nan 0.05 7.29 0.67 0.66 279.3 386 3.6 383 850139496 0.39 0.77 4.11 3.53 1.03 0.1 0 0 good 0.34 58.93 0 -0.11 15.42
951777474 0.03069 100 -7.31 nan 0.03 2.95 0.5 0.62 243.94 387 2 384 850139518 0.44 0.77 nan 0 0.79 0.1 0.5 0 good 0.69 22.42 0.25 -0.13 287.78
951777480 0.06975 120 -8.83 nan 0.07 4.4 0.18 0.62 108.78 388 1.3 385 850139518 0.82 0.96 20.1 6.73 0.41 0.11 0.16 0 good -3.04 25.47 0.19 -0.07 47.9
951777485 0.40177 140 0.34 0.06 0.4 4.01 0.36 1.33 27.11 389 0.9 386 850139526 4.1 0.91 48.53 362.25 0.01 2.02 0.17 0 noise -0.25 34.27 0.05 -0.02 10.32
951777492 0.04919 100 -2.06 nan 0.05 3.92 0.11 0.15 140.06 390 2.24 387 850139632 1.04 0.67 35.16 34.73 0.46 0.21 0.14 0 good -0.26 28.23 0.02 -0.37 0
951777499 0.24739 160 0 0.14 0.25 nan nan 2.35 175.97 391 1.77 388 850139652 2.11 0.99 120.86 1007.86 0.03 1.21 0.01 0 noise -7.38 nan nan -3.65 7.59
951777504 0.42574 140 -1.55 -0.07 0.43 3.16 0.56 1.47 74.23 392 1.2 389 850139642 2.6 0.99 71.76 445.89 0.02 nan 0.01 0 good 0.25 29.84 0.03 nan 0.85
951777511 0.13516 60 -1.03 -0.08 0.14 5.29 0.52 0.66 241.82 393 2.98 390 850139642 0.46 0.87 9.62 69.27 0.86 0.14 0.03 0 good -0.07 41.86 0 -0.06 2.12
951777517 0.09641 70 -0.48 0.07 0.1 4.59 0.17 0.67 207.73 394 2.32 391 850139642 0.49 0.89 22.31 62.45 0.69 0.14 0.2 0 good -0.48 34.29 0.01 -0.04 4.17
951777523 1.61256 50 -2.06 0.08 1.61 5.58 0.97 0.73 153.81 395 2.06 392 850139650 0.43 0.61 32.16 99.38 0.49 1.04 0 0 good -0.14 74.62 0 -0.05 0.16
951777528 0.82524 170 0.03 0.1 0.83 3.52 0.75 0.88 35.9 396 0.87 393 850139728 1.71 0.99 30.88 460.37 0.03 nan 0.32 0 noise 0.11 40.09 0.02 0 13.19
951777534 0.03792 40 0.69 nan 0.04 5.95 0.19 0.73 85.58 397 3.19 394 850139720 0.24 0.51 13.18 7.98 0.27 0.19 0.04 0 good 0.34 37.35 0 -0.05 0
951777540 0.1177 70 0.48 -0.11 0.12 4.63 0.64 0.62 64.43 398 0.78 395 850139742 0.41 0.79 11.87 55.27 0.17 1.06 0.02 0 good 1.03 38.6 0.01 -0.01 0
951777548 0.20078 100 0.18 nan 0.2 3.17 0.81 0.6 94.21 399 2.23 396 850139864 0.3 0.92 19.62 68.93 0.14 0.63 0.03 0 noise 0 19 0.3 -0.07 54.75
951777553 2.35957 60 -0.82 0.05 2.36 5.76 0.98 0.65 67.12 400 2.1 397 850139294 0.05 0.99 18.47 190.93 0.19 0.29 0.01 0 good 0.34 96.63 0 -0.03 0.02
951777559 0.02108 110 -2.59 nan 0.02 2.95 0 1.19 54.81 401 1.55 398 850139336 3.38 0.59 nan 0 0.02 2.5 0.5 0 good 1.04 34.35 0 -0.02 0
951777565 0.08143 140 0.46 nan 0.08 4.37 0.29 1.21 44.52 402 1.28 399 850139526 2.35 0.74 28.15 61.94 0.02 0.78 0.08 0 noise -0.45 26 0.09 -0 175.21
951777571 0.20088 70 0.69 nan 0.2 6.03 0.82 0.71 96.61 403 2.42 400 850139738 0.24 0.78 28.06 129.75 0.22 0.18 0 0 good 1.14 61.69 0 -0.03 0
951777576 0.01085 80 -0.96 nan 0.01 2.28 nan 1.21 65.4 404 1.78 401 850139338 1.63 0.35 nan 0 0.04 1.15 0.5 0 good 0.21 38.59 0 -0 0
951777582 0.1457 140 -3.49 -0.08 0.15 5.2 0.43 0.71 71.31 405 1.32 402 850139622 0.29 0.85 13.06 116.66 0.15 0.56 0.04 0 good -0.64 28.24 0.02 -0.02 3.65
951777593 0.0464 90 nan nan 0.05 3.83 0.59 0.56 113.65 406 2.82 403 850139620 0.44 0.55 4.52 1.92 0.3 0.25 0.04 0 good -0.97 32.79 0.01 -0.02 0
951777600 0.0621 60 -0.69 nan 0.06 6.12 0.25 0.73 282.69 407 4.5 404 850139642 0.39 0.65 11.86 19.43 0.97 0.12 0 0 good 0 48.98 0 -0.06 0
Taking a closer look at the columns, we can see there is a lot of information we do not need. We are solely interested in predicting the spiking activity from the neurons from VISp. Thus, we will remove the metadata from all columns except for rate, quality (to make sure we filter the bad-quality neurons) and peak_channel_id (this last one contains relevant information for brain area identification).
def restrict_cols(cols_to_keep, data):
cols_to_remove = [col for col in data.metadata_columns if col not in cols_to_keep]
data.drop_info(cols_to_remove)
# Choose which columns to remove and remove them
cols_to_keep = ['rate', 'quality','peak_channel_id']
restrict_cols(cols_to_keep,units)
# See the dataset
print(units)
Index rate peak_channel_id quality
--------- -------- ----------------- ---------
951763702 2.38003 850135036 good
951763707 0.01147 850135036 noise
951763711 3.1503 850135038 good
951763715 6.53 850135038 good
951763720 2.00296 850135044 good
951763724 8.66233 850135044 noise
951763729 11.134 850135044 noise
951763733 23.8915 850135050 good
951763737 1.01848 850135050 noise
951763741 11.8133 850135050 noise
951763745 13.4006 850135050 noise
951763749 18.2252 850135050 noise
951763753 18.9817 850135050 noise
951763758 13.2587 850135050 noise
951763762 17.3762 850135050 noise
951763766 12.0932 850135050 noise
951763770 4.00705 850135064 noise
951763774 5.77131 850135052 good
951763778 1.15881 850135052 noise
951763782 14.6012 850135058 good
951763786 7.50032 850135058 good
951763790 0.50676 850135058 good
951763794 13.4125 850135060 noise
951763798 3.45524 850135060 good
951763802 14.2516 850135062 good
951763806 2.36639 850135072 good
951763808 10.4327 850135050 good
951763811 0.91494 850135062 noise
951763815 8.95715 850135062 noise
951763819 0.69669 850135062 good
951763823 15.7534 850135064 good
951763828 20.426 850135066 good
951763833 5.54128 850135068 good
951763837 10.3832 850135068 good
951763841 18.6182 850135068 good
951763845 12.7977 850135068 good
951763849 11.4132 850135070 good
951763854 2.52108 850135070 noise
951763859 17.1477 850135072 good
951763863 0.59377 850135072 good
951763867 0.03658 850135072 good
951763874 0.01312 850135072 noise
951763880 0.02273 850135478 noise
951763887 5.85025 850135076 good
951763893 5.0215 850135078 good
951763901 6.27197 850135086 good
951763907 9.34383 850135082 good
951763914 15.789 850135084 good
951763920 4.00488 850135084 good
951763928 5.38287 850135084 good
951763934 3.04221 850135084 good
951763941 0.00816 850135084 noise
951763947 1.57897 850135084 noise
951763954 11.8275 850135086 good
951763961 8.62689 850135086 good
951763968 8.3856 850135088 good
951763975 14.9898 850135090 good
951763982 12.1488 850135092 good
951763988 7.26286 850135092 good
951763994 5.46647 850135092 noise
951764001 11.7287 850135094 good
951764008 0.15738 850135094 good
951764014 2.82003 850135122 noise
951764022 11.1967 850135096 good
951764029 5.63883 850135090 good
951764035 11.5555 850135100 good
951764042 12.2763 850135100 good
951764049 3.296 850135100 good
951764055 7.28983 850135102 good
951764063 7.33901 850135102 good
951764070 10.6127 850135102 good
951764076 3.39117 850135102 good
951764083 10.1095 850135102 good
951764090 14.326 850135104 good
951764099 11.0116 850135108 good
951764106 12.9879 850135108 good
951764112 8.86983 850135108 good
951764118 4.8696 850135112 good
951764125 4.77381 850135110 good
951764132 11.0504 850135110 good
951764139 6.14549 850135110 good
951764147 7.73138 850135112 good
951764155 7.7847 850135112 good
951764162 3.00635 850135114 good
951764169 0.58705 850135112 good
951764175 11.2825 850135120 good
951764182 3.69808 850135116 good
951764190 8.31926 850135116 good
951764196 2.44906 850135120 good
951764203 14.0843 850135122 good
951764210 5.32293 850135124 good
951764216 19.1162 850135124 good
951764224 3.83655 850135124 good
951764232 5.33502 850135118 good
951764239 3.92841 850135126 good
951764246 5.55037 850135126 good
951764250 6.62693 850135128 good
951764254 0.49198 850135130 noise
951764259 7.92751 850135132 good
951764263 5.8641 850135128 good
951764268 4.06389 850135134 good
951764272 14.842 850135134 good
951764276 1.14734 850135134 noise
951764279 10.7474 850135138 good
951764284 4.16102 850135138 good
951764287 4.80088 850135140 good
951764293 16.162 850135140 good
951764299 9.321 850135140 good
951764305 12.0763 850135142 good
951764312 13.7481 850135142 good
951764319 2.25282 850135142 good
951764325 14.3434 850135146 good
951764332 6.43751 850135148 good
951764338 6.4588 850135148 good
951764344 12.0088 850135150 good
951764350 10.6634 850135150 good
951764357 11.6866 850135150 good
951764364 6.12068 850135150 good
951764370 14.4044 850135152 good
951764374 4.53159 850135152 good
951764379 4.49532 850135156 good
951764385 8.29497 850135156 good
951764390 3.70893 850135156 good
951764396 5.75643 850135156 good
951764403 1.74472 850135156 noise
951764409 2.02507 850135156 noise
951764415 22.8442 850135158 good
951764421 11.9241 850135158 good
951764426 2.71742 850135158 noise
951764432 14.0462 850135158 good
951764438 22.7161 850135160 good
951764443 14.2488 850135162 good
951764447 3.7575 850135164 good
951764454 8.93462 850135164 good
951764460 20.9761 850135166 good
951764466 3.91136 850135166 good
951764472 15.2495 850135168 good
951764478 17.1805 850135170 good
951764484 5.14984 850135172 good
951764490 3.234 850135172 good
951764496 10.2851 850135172 good
951764503 20.7697 850135170 good
951764508 3.69643 850135174 good
951764514 12.4374 850135170 good
951764520 10.2671 850135176 good
951764525 5.52423 850135174 good
951764531 12.6207 850135180 noise
951764537 11.6708 850135180 noise
951764543 3.67886 850135180 good
951764550 4.92685 850135180 good
951764557 9.14284 850135180 good
951764563 10.5269 850135182 good
951764570 11.5479 850135182 good
951764576 6.09557 850135182 noise
951764582 3.42961 850135182 noise
951764589 5.32965 850135182 noise
951764595 6.93115 850135182 noise
951764601 3.70697 850135182 noise
951764608 18.6999 850135182 good
951764614 15.2261 850135186 good
951764618 1.6015 850135186 good
951764622 13.3591 850135182 good
951764624 13.0301 850135188 good
951764626 11.5823 850135188 good
951764630 7.20716 850135190 good
951764635 5.02522 850135192 good
951764639 10.251 850135196 good
951764644 13.5192 850135196 good
951764648 8.21975 850135196 good
951764652 6.23229 850135196 good
951764656 5.28139 850135196 noise
951764663 0.00093 850135196 noise
951764669 3.9993 850135198 good
951764675 4.10233 850135198 good
951764681 1.56647 850135200 good
951764688 1.50726 850135198 good
951764694 2.66358 850135202 good
951764700 4.42691 850135204 good
951764706 10.0951 850135206 good
951764714 3.74241 850135206 good
951764718 9.8384 850135210 noise
951764724 10.5901 850135212 good
951764731 12.0302 850135212 good
951764739 1.05082 850135212 noise
951764746 0.00227 850135170 noise
951764753 9.52085 850135214 good
951764761 8.88574 850135214 noise
951764768 9.13933 850135214 good
951764776 3.37133 850135216 good
951764783 23.1542 850135216 good
951764791 5.49003 850135216 good
951764798 10.1731 850135216 good
951764809 20.4946 850135218 noise
951764815 0.83423 850135220 noise
951764821 0.83144 850135220 noise
951764827 0.0031 850135196 noise
951764835 9.1322 850135270 noise
951764842 2.50341 850135318 good
951764848 0.71105 850135324 good
951764855 4.23894 850135332 good
951764862 2.10123 850135334 good
951764868 13.3805 850135334 good
951764875 1.47967 850135334 good
951764883 3.91798 850135338 noise
951764889 7.6392 850135338 noise
951764895 5.06408 850135340 good
951764903 6.99842 850135340 good
951764909 3.95053 850135340 noise
951764916 0.01033 850135340 noise
951764923 0.00558 850135340 noise
951764928 0.00765 850135340 noise
951764935 0.01354 850135340 noise
951764939 0.00827 850135340 noise
951764944 4.10667 850135342 noise
951764951 2.11601 850135342 good
951764958 2.80133 850135344 noise
951764964 4.36522 850135326 noise
951764971 1.73925 850135344 noise
951764977 3.93389 850135344 noise
951764983 3.26614 850135326 noise
951764990 1.58476 850135344 noise
951764995 1.82656 850135344 noise
951765001 0.65494 850135344 noise
951765009 18.7407 850135356 good
951765017 1.72437 850135372 noise
951765023 2.14391 850135374 good
951765031 6.40951 850135368 noise
951765039 6.89932 850135368 noise
951765044 6.80167 850135368 noise
951765049 0.0031 850135370 noise
951765055 0.04092 850135370 noise
951765061 0.04764 850135372 good
951765067 1.06364 850135372 good
951765074 0.86037 850135372 noise
951765080 3.61148 850135376 noise
951765085 0.00713 850135372 noise
951765093 0.0125 850135376 noise
951765098 0.62353 850135380 good
951765105 17.799 850135368 noise
951765110 3.41453 850135376 noise
951765118 1.60491 850135388 noise
951765124 10.2191 850135368 noise
951765132 6.29749 850135390 noise
951765138 4.64836 850135390 noise
951765145 5.76635 850135390 good
951765151 12.9111 850135416 good
951765159 25.3179 850135424 noise
951765164 8.99611 850135418 noise
951765170 5.02088 850135430 noise
951765176 2.50662 850135430 good
951765182 10.2026 850135430 good
951765189 3.2618 850135426 noise
951765195 0.83537 850135418 noise
951765200 0.81367 850135450 noise
951765206 0.65071 850135444 noise
951765213 0.47751 850135450 good
951765219 0.00651 850135460 noise
951765225 5.07885 850135454 good
951765231 2.53317 850135470 noise
951765238 2.03313 850135452 noise
951765243 5.11461 850135460 good
951765247 7.2672 850135470 noise
951765252 4.16857 850135470 good
951765258 9.5782 850135470 good
951765264 2.62855 850135478 good
951765270 2.10805 850135466 good
951765276 6.53124 850135470 good
951765282 2.79348 850135470 good
951765288 9.12827 850135474 good
951765293 5.05044 850135472 good
951765299 4.3677 850135474 good
951765303 6.53413 850135478 good
951765309 2.50352 850135478 good
951765314 9.83788 850135478 good
951765319 0.90471 850135474 good
951765323 3.66574 850135476 good
951765329 4.50648 850135476 good
951765334 6.26566 850135476 good
951765339 1.33551 850135480 good
951765343 4.19781 850135478 good
951765349 10.8901 850135478 good
951765353 3.54545 850135480 good
951765358 2.30501 850135478 good
951765364 39.3285 850135482 good
951765369 13.1377 850135484 good
951765374 0.32385 850135478 noise
951765379 2.20085 850135478 noise
951765385 0.00785 850135476 good
951765393 5.09063 850135478 noise
951765396 0.00289 850135492 noise
951765400 16.8106 850135494 noise
951765405 33.1885 850135494 good
951765411 11.0497 850135494 noise
951765414 5.89448 850135496 good
951765420 13.1448 850135498 good
951765423 14.1916 850135500 good
951765430 5.69876 850135504 good
951765435 19.8853 850135506 good
951765440 9.97935 850135520 good
951765447 1.86221 850135522 good
951765454 5.47349 850135526 good
951765460 4.44892 850135526 good
951765467 9.98162 850135528 good
951765473 4.10409 850135528 noise
951765478 17.4047 850135532 good
951765485 13.9773 850135532 good
951765490 5.27323 850135528 noise
951765497 8.33011 850135532 noise
951765502 13.287 850135532 noise
951765508 2.13461 850135532 good
951765513 3.90661 850135534 noise
951765520 24.5397 850135538 noise
951765525 12.0324 850135538 noise
951765530 2.95127 850135540 good
951765535 3.3674 850135540 good
951765541 1.58972 850135538 good
951765547 3.5935 850135542 good
951765552 2.32971 850135542 good
951765557 4.0796 850135538 good
951765561 1.76766 850135546 good
951765566 3.18388 850135548 good
951765571 2.77426 850135550 good
951765576 12.7688 850135550 noise
951765582 14.778 850135550 good
951765587 2.62793 850135552 good
951765594 2.76868 850135548 good
951765600 0.00796 850135558 noise
951765606 7.46973 850135564 good
951765611 23.9673 850135566 good
951765617 2.60169 850135566 good
951765623 6.50075 850135568 good
951765629 3.00129 850135570 good
951765635 0.11336 850135570 noise
951765641 4.34527 850135572 good
951765647 9.12497 850135574 good
951765653 9.42195 850135576 good
951765661 15.6626 850135578 good
951765666 9.72245 850135576 good
951765669 5.41325 850135580 good
951765675 18.6652 850135580 good
951765681 14.6917 850135580 good
951765686 11.2814 850135582 good
951765692 1.13855 850135582 good
951765697 9.08022 850135584 good
951765703 3.58978 850135578 noise
951765710 0.003 850135584 noise
951765716 3.34756 850135590 good
951765721 10.0994 850135588 good
951765727 15.782 850135588 good
951765732 1.64645 850135590 good
951765737 6.97155 850135596 good
951765743 10.5288 850135598 noise
951765747 13.0858 850135598 noise
951765753 13.4251 850135598 noise
951765758 13.2055 850135598 noise
951765764 19.5368 850135598 noise
951765769 7.64943 850135598 good
951765775 0.31001 850135602 noise
951765780 0.00289 850135602 noise
951765786 2.58722 850135604 good
951765793 7.54827 850135612 good
951765801 1.88846 850135606 good
951765809 5.72387 850135602 good
951765815 0.00713 850135602 noise
951765820 5.49643 850135610 good
951765825 1.98983 850135612 good
951765832 5.27602 850135624 noise
951765836 1.17183 850135622 noise
951765841 0.00858 850135614 noise
951765849 1.28302 850135622 noise
951765855 1.28787 850135628 good
951765859 0.18828 850135628 noise
951765866 3.43602 850135630 good
951765870 0.45974 850135636 noise
951765876 0.00134 850135636 noise
951765881 1.33448 850135642 good
951765886 3.61417 850135642 good
951765892 0.73668 850135648 good
951765898 21.7077 850135690 noise
951765904 0.91411 850135684 noise
951765910 10.1545 850135690 noise
951765913 10.8102 850135072 good
951765921 0.11367 850135072 good
951765926 9.27046 850135112 good
951765931 5.00807 850135118 good
951765944 1.90417 850135172 good
951765950 1.62072 850135174 good
951765955 0.16513 850135324 good
951765961 0.948 850135334 good
951765966 0.10117 850135374 good
951765973 0.67416 850135372 good
951765977 0.50407 850135380 good
951765984 0.12969 850135448 noise
951765988 0.45085 850135470 good
951765995 1.32508 850135604 good
951766001 0.1395 850135684 noise
951766007 0.57589 850135330 good
951766012 0.09083 850135474 good
951766019 0.02501 850135372 good
951766024 0.00837 850135372 good
951766138 3.56684 850137692 good
951766144 10.9933 850137694 good
951766152 7.44338 850137694 good
951766160 4.75634 850137694 good
951766167 10.7141 850137696 good
951766173 9.36047 850137696 good
951766180 10.412 850137692 good
951766188 5.87175 850137698 good
951766195 8.16663 850137696 good
951766203 1.90221 850137702 good
951766208 12.5293 850137702 good
951766214 0.0589 850137702 noise
951766220 0.17577 850137696 good
951766225 5.32087 850137700 good
951766229 4.65135 850137704 good
951766235 0.96609 850137704 good
951766240 5.05385 850137702 good
951766245 3.38342 850137706 good
951766251 6.44888 850137706 good
951766256 0.70733 850137706 good
951766262 6.33583 850137710 good
951766266 8.58318 850137710 good
951766271 6.02665 850137710 good
951766276 2.62132 850137712 good
951766280 4.53841 850137712 good
951766286 6.32157 850137712 good
951766291 2.9985 850137712 good
951766298 8.71307 850137714 good
951766303 9.10947 850137716 good
951766309 27.6031 850137718 good
951766314 13.9623 850137718 good
951766322 13.2362 850137718 good
951766327 20.8808 850137720 good
951766334 9.46226 850137716 good
951766340 3.49089 850137720 good
951766346 7.1218 850137720 good
951766353 0.01281 850137720 good
951766360 0.39991 850137722 good
951766366 10.6936 850137724 good
951766372 12.1386 850137724 good
951766379 6.03647 850137726 good
951766385 3.86827 850137726 good
951766390 6.73223 850137726 good
951766398 1.86687 850137736 good
951766403 7.8248 850137730 good
951766408 10.6266 850137730 good
951766416 10.091 850137732 good
951766421 0.68915 850137738 good
951766427 7.16882 850137734 good
951766432 7.59136 850137734 good
951766438 5.55885 850137736 good
951766442 9.71284 850137736 good
951766447 13.6457 850137738 good
951766452 5.53095 850137738 good
951766458 15.2865 850137742 good
951766463 8.09647 850137742 good
951766469 0.06086 850137742 good
951766474 15.4068 850137742 good
951766480 6.592 850137744 good
951766485 1.00887 850137744 good
951766489 5.3901 850137748 good
951766494 5.21226 850137750 good
951766500 0.344 850137750 good
951766504 7.791 850137752 good
951766510 3.71916 850137752 good
951766515 14.5508 850137752 good
951766521 10.2152 850137750 good
951766526 7.57307 850137754 good
951766531 8.37578 850137754 good
951766541 15.5747 850137756 good
951766546 12.2331 850137758 good
951766552 6.38915 850137758 good
951766557 4.74549 850137758 good
951766562 0.16058 850137758 good
951766567 1.90572 850137758 good
951766573 14.5612 850137760 good
951766577 2.15807 850137766 good
951766582 6.21069 850137766 good
951766589 13.1292 850137766 good
951766593 2.40938 850137766 good
951766599 10.8013 850137766 good
951766605 0.91628 850137768 noise
951766611 8.05554 850137770 good
951766616 4.09551 850137774 good
951766621 4.53768 850137776 good
951766625 7.22948 850137778 good
951766630 17.7724 850137778 good
951766634 5.82938 850137780 good
951766636 10.1654 850137780 good
951766640 14.9032 850137782 good
951766645 9.48799 850137782 good
951766650 9.78735 850137782 good
951766657 4.37906 850137784 good
951766662 8.9896 850137784 good
951766673 19.209 850137786 good
951766679 4.43683 850137786 good
951766685 5.74878 850137790 good
951766691 0.12307 850137792 good
951766697 9.43415 850137792 good
951766704 14.0932 850137792 good
951766709 3.67142 850137800 good
951766714 5.80851 850137796 good
951766722 4.83012 850137798 good
951766727 7.53411 850137798 noise
951766732 9.49439 850137798 good
951766738 0.03865 850137800 good
951766743 6.11428 850137800 good
951766749 10.5625 850137802 good
951766754 4.75293 850137804 good
951766761 2.22317 850137804 noise
951766767 6.77501 850137804 good
951766773 5.93778 850137806 good
951766780 9.65053 850137808 noise
951766785 0.00289 850137806 noise
951766791 12.2685 850137810 good
951766797 9.73103 850137810 good
951766803 1.74886 850137810 good
951766809 5.3809 850137812 good
951766816 13.8656 850137808 good
951766820 4.09675 850137814 noise
951766828 3.99424 850137814 good
951766833 3.1071 850137816 good
951766840 0.74164 850137816 good
951766846 3.07569 850137816 good
951766853 0.11636 850137818 good
951766860 0.19882 850137818 good
951766867 5.40002 850137816 good
951766873 6.75093 850137820 good
951766879 10.7436 850137820 good
951766886 1.85229 850137820 good
951766893 6.92133 850137822 good
951766899 6.3007 850137822 good
951766906 4.72048 850137822 good
951766912 6.60729 850137824 good
951766918 0.34101 850137824 good
951766923 1.02189 850137824 good
951766928 1.23497 850137828 good
951766933 0.08133 850137828 good
951766938 6.78389 850137828 good
951766942 7.80795 850137830 good
951766948 6.11903 850137830 good
951766952 13.0386 850137830 good
951766957 1.97123 850137832 good
951766960 1.76363 850137832 good
951766965 6.69885 850137834 good
951766968 1.38088 850137836 good
951766973 0.0062 850137838 good
951766978 4.07247 850137838 noise
951766983 0.16131 850137838 good
951766990 12.6832 850137838 good
951766995 1.32249 850137838 good
951767001 2.79089 850137840 good
951767006 3.95456 850137840 good
951767013 1.88857 850137840 good
951767020 1.77717 850137840 noise
951767025 2.16158 850137840 noise
951767033 0.14818 850137840 noise
951767038 1.78885 850137844 good
951767045 5.89758 850137844 good
951767050 11.6229 850137844 good
951767056 5.01468 850137846 good
951767061 4.74084 850137846 good
951767067 5.18054 850137848 good
951767074 8.54753 850137848 good
951767078 2.8839 850137848 good
951767086 17.4824 850137848 noise
951767092 2.35626 850137850 good
951767098 6.15344 850137852 good
951767104 1.92845 850137852 noise
951767108 5.38793 850137854 good
951767112 9.06679 850137854 good
951767120 4.13839 850137854 good
951767125 3.19928 850137854 noise
951767133 3.54359 850137854 good
951767138 3.67855 850137856 good
951767144 4.2285 850137856 good
951767152 8.61593 850137856 good
951767157 1.58776 850137856 noise
951767164 9.383 850137974 noise
951767169 3.17086 850137992 noise
951767177 2.97917 850137976 noise
951767182 7.54455 850137982 noise
951767190 0.09238 850137996 good
951767195 2.75473 850137992 good
951767202 3.80731 850138002 noise
951767209 5.08578 850138002 good
951767217 0.1054 850138002 good
951767223 6.24179 850138006 good
951767230 0.08897 850138002 good
951767242 10.0404 850138010 good
951767247 1.57566 850138014 good
951767253 8.11517 850138022 good
951767258 4.49191 850138018 noise
951767263 3.47787 850138016 noise
951767269 1.71785 850138016 noise
951767274 0.48785 850138024 noise
951767280 13.4059 850138016 good
951767285 1.1801 850138018 good
951767291 7.60314 850138024 noise
951767297 5.39754 850138024 noise
951767304 1.49341 850138030 good
951767310 20.5422 850138032 good
951767318 0.76107 850138036 good
951767322 0.1455 850138032 good
951767329 3.09563 850138036 noise
951767334 5.63676 850138026 noise
951767340 4.63348 850138052 noise
951767346 6.02128 850138056 noise
951767351 1.51118 850138056 noise
951767358 0.50418 850138056 noise
951767364 0.4586 850138056 noise
951767370 5.1362 850138058 noise
951767376 3.00521 850138090 noise
951767383 2.80598 850138088 noise
951767389 0.93684 850138088 noise
951767395 1.53702 850138088 noise
951767402 1.03677 850138088 noise
951767408 0.03968 850138088 noise
951767415 0.16286 850138036 noise
951767422 3.12963 850138092 noise
951767428 0.00806 850138096 noise
951767433 0.48826 850138098 noise
951767438 4.72493 850138110 good
951767443 0.44 850138104 noise
951767450 0.01478 850138104 noise
951767455 2.51437 850138106 good
951767461 1.6666 850138108 good
951767468 6.65524 850138110 noise
951767474 4.99029 850138116 noise
951767481 2.13409 850138114 good
951767487 15.1874 850138114 good
951767493 0.00765 850138114 noise
951767500 2.84287 850138116 good
951767507 1.90045 850138116 noise
951767514 1.88309 850138114 good
951767520 2.06217 850138120 good
951767526 2.5247 850138136 noise
951767532 6.72251 850138122 good
951767538 0.62498 850138130 good
951767544 0.76841 850138142 good
951767547 0.21701 850138126 noise
951767552 0.27684 850138126 noise
951767556 2.96853 850138122 noise
951767562 0.29637 850138136 noise
951767566 0.71446 850138132 good
951767573 7.00834 850138138 good
951767580 0.01715 850138132 good
951767586 5.66043 850138134 good
951767594 3.2216 850138150 good
951767599 1.25687 850138136 noise
951767606 1.26183 850138136 good
951767612 6.88134 850138140 good
951767618 4.13209 850138138 good
951767624 3.92211 850138138 good
951767631 0.00496 850138142 good
951767636 0.19076 850138142 noise
951767643 4.95309 850138140 good
951767649 6.09692 850138140 good
951767655 1.171 850138142 good
951767661 7.66545 850138142 good
951767667 1.09298 850138142 good
951767674 0.24584 850138142 good
951767681 0.22228 850138142 good
951767688 1.44722 850138142 noise
951767694 0.24387 850138142 noise
951767700 0.04929 850138142 good
951767707 0.01829 850138142 noise
951767713 17.364 850138144 good
951767719 1.35949 850138148 good
951767725 14.6946 850138148 good
951767730 13.7188 850138148 good
951767738 2.12593 850138148 good
951767743 1.28085 850138128 noise
951767750 1.1275 850138150 good
951767757 0.86709 850138150 good
951767763 0.25875 850138142 good
951767770 2.86085 850138150 good
951767776 2.16685 850138160 noise
951767782 1.31753 850138152 good
951767789 4.99897 850138152 good
951767795 2.74997 850138152 good
951767803 4.23677 850138154 good
951767810 2.37765 850138154 good
951767821 4.38216 850138148 good
951767827 4.35674 850138162 good
951767832 3.53626 850138156 good
951767838 2.72631 850138160 good
951767845 0.74929 850138150 noise
951767852 0.26867 850138158 noise
951767857 1.92391 850138158 good
951767862 0.6289 850138150 noise
951767868 2.15331 850138166 noise
951767873 2.78717 850138160 good
951767879 1.65482 850138160 good
951767884 0.02883 850138162 good
951767892 0.20926 850138164 good
951767897 26.7566 850138164 good
951767903 4.96601 850138160 good
951767907 1.15405 850138166 good
951767915 2.33498 850138166 good
951767920 11.689 850138166 good
951767927 4.05283 850138160 good
951767933 1.48814 850138168 good
951767939 3.34074 850138168 good
951767945 4.65301 850138168 good
951767950 11.2101 850138168 good
951767956 3.27482 850138168 good
951767960 7.71826 850138168 good
951767966 7.05711 850138170 good
951767973 1.25284 850138170 good
951767979 2.99633 850138172 good
951767984 0.48289 850138172 good
951767991 5.21691 850138174 good
951767997 2.56841 850138174 good
951768004 4.48581 850138174 good
951768010 4.42339 850138176 good
951768018 8.212 850138176 good
951768023 4.26932 850138176 good
951768030 2.22027 850138176 good
951768035 3.24588 850138176 noise
951768042 3.34725 850138176 noise
951768047 2.89165 850138172 good
951768054 18.1724 850138182 good
951768060 0.46429 850138176 noise
951768067 3.65075 850138184 good
951768073 2.28259 850138176 noise
951768080 1.55624 850138184 good
951768086 0.1579 850138188 good
951768093 3.65344 850138190 good
951768098 4.65538 850138190 noise
951768105 13.1174 850138190 good
951768109 2.4225 850138192 noise
951768115 0.42089 850138192 noise
951768121 0.28893 850138200 noise
951768127 3.07114 850138208 noise
951768133 12.0295 850138212 good
951768139 4.95733 850138212 good
951768144 3.58524 850138214 noise
951768149 3.98442 850138214 noise
951768154 5.94749 850138216 good
951768160 2.84969 850138216 good
951768165 5.99213 850138214 noise
951768170 4.00664 850138214 good
951768177 2.6113 850138222 good
951768183 5.32107 850138224 good
951768188 3.62843 850138234 good
951768196 1.16005 850138224 good
951768201 4.48178 850138224 noise
951768209 1.65337 850138224 good
951768215 2.43232 850138224 good
951768222 38.6918 850138226 good
951768228 1.4528 850138228 good
951768234 0.04402 850138230 good
951768239 2.24094 850138230 good
951768247 6.3691 850138232 good
951768252 0.95854 850138232 good
951768258 2.92234 850138232 good
951768266 1.54962 850138232 good
951768272 0.11047 850138238 good
951768278 9.61519 850138238 good
951768285 3.60332 850138238 good
951768291 2.06661 850138238 good
951768298 7.5058 850138240 good
951768307 3.44108 850138240 good
951768313 2.51974 850138238 noise
951768318 11.362 850138246 good
951768327 1.25057 850138246 good
951768332 18.085 850138248 good
951768340 2.44038 850138248 good
951768345 4.23646 850138248 good
951768352 1.72974 850138252 good
951768356 3.20248 850138258 noise
951768363 1.26452 850138258 good
951768369 4.01356 850138254 good
951768374 10.5394 850138254 good
951768382 11.6807 850138256 good
951768390 27.369 850138258 good
951768402 7.5028 850138262 good
951768408 11.9073 850138260 good
951768415 1.64232 850138260 good
951768421 11.2489 850138262 good
951768427 5.18322 850138262 good
951768434 10.6732 850138262 good
951768441 23.9354 850138264 good
951768446 14.5898 850138264 good
951768451 11.3477 850138264 good
951768457 9.15917 850138266 good
951768462 3.18564 850138264 good
951768467 1.92143 850138268 good
951768473 8.20703 850138270 good
951768480 5.17423 850138270 good
951768487 0.31145 850138270 good
951768495 16.5755 850138272 good
951768500 11.2425 850138272 good
951768506 0.13651 850138272 good
951768511 6.84621 850138272 good
951768519 0.21856 850138274 good
951768524 4.24338 850138270 good
951768530 2.67815 850138276 good
951768538 4.26591 850138276 good
951768544 2.18772 850138276 good
951768550 2.01825 850138278 good
951768557 7.48875 850138278 good
951768563 1.62082 850138278 good
951768568 7.46457 850138278 good
951768575 1.83111 850138280 good
951768581 4.42153 850138280 good
951768586 2.11725 850138280 good
951768593 2.39016 850138282 good
951768598 1.75857 850138282 good
951768604 6.47378 850138284 good
951768611 0.82968 850138284 good
951768616 1.5769 850138284 good
951768621 3.24547 850138286 good
951768627 11.0219 850138286 good
951768632 4.57457 850138286 good
951768637 2.74026 850138288 noise
951768643 1.4684 850138288 good
951768649 5.50615 850138288 good
951768655 2.28073 850138288 good
951768660 0.7403 850138290 good
951768668 2.53855 850138290 good
951768673 1.92969 850138294 good
951768681 0.49353 850138292 good
951768686 3.26159 850138294 noise
951768693 2.85889 850138294 good
951768699 4.46896 850138294 good
951768705 4.19585 850138296 good
951768712 4.65549 850138296 good
951768717 1.42169 850138296 good
951768723 5.12256 850138296 good
951768729 1.35205 850138294 noise
951768735 0.81573 850138300 good
951768739 1.94953 850138300 good
951768745 2.27897 850138296 noise
951768749 2.02352 850138302 good
951768754 1.3661 850138302 good
951768760 4.04994 850138294 noise
951768766 8.87438 850138304 good
951768771 8.05575 850138304 noise
951768776 0.03441 850138308 good
951768782 0.1641 850138310 good
951768786 3.67638 850138310 noise
951768793 4.23739 850138302 good
951768797 0.88393 850138312 good
951768802 0.00651 850138314 good
951768807 2.17615 850138312 good
951768810 2.27835 850138302 noise
951768815 2.70812 850138318 good
951768820 5.31446 850138304 noise
951768823 6.52535 850138320 good
951768830 10.9098 850138320 good
951768835 7.83947 850138324 good
951768842 2.49308 850138320 good
951768848 4.81886 850138320 noise
951768854 3.75047 850138312 noise
951768861 0.24088 850138326 good
951768867 0.03813 850138324 good
951768875 0.94707 850138322 good
951768881 2.06258 850138326 good
951768888 2.90921 850138328 good
951768894 9.16155 850138328 good
951768901 3.99186 850138330 good
951768907 2.85765 850138332 good
951768913 0.0712 850138332 good
951768920 1.85539 850138334 good
951768925 2.28806 850138336 good
951768932 0.78329 850138336 noise
951768937 0.08412 850138340 good
951768944 0.96981 850138344 good
951768950 0.37893 850138364 noise
951768957 10.2835 850138394 noise
951768969 6.83019 850138376 noise
951768974 1.00556 850138394 noise
951768980 6.48257 850137694 good
951768986 8.03663 850137696 good
951768990 1.87875 850137708 good
951768995 4.25578 850137712 good
951769002 0.03389 850137722 good
951769007 15.5288 850137738 good
951769012 1.77727 850137738 good
951769018 2.70678 850137742 good
951769024 7.12573 850137742 good
951769029 11.3657 850137740 good
951769034 10.5122 850137750 good
951769041 1.54229 850137756 good
951769046 6.2699 850137758 good
951769054 2.17036 850137780 good
951769060 2.35905 850137792 good
951769068 3.05016 850137792 good
951769074 0.03823 850137792 good
951769081 14.6808 850137796 good
951769088 2.94218 850137800 good
951769094 7.31804 850137816 good
951769100 2.82582 850137818 good
951769106 7.54703 850137818 good
951769112 2.67371 850137824 good
951769119 6.08782 850137816 good
951769125 2.68911 850137816 good
951769131 1.97671 850137828 good
951769138 2.61677 850137832 good
951769144 1.13215 850137838 good
951769149 3.25725 850137848 good
951769156 1.14785 850137986 good
951769162 0.04485 850137986 good
951769169 0.04433 850138002 good
951769174 1.73439 850138006 noise
951769182 0.13651 850138002 good
951769187 1.45662 850138052 noise
951769194 1.14785 850138088 noise
951769200 0.28438 850138088 noise
951769207 0.01054 850138088 noise
951769213 0.0156 850138088 noise
951769220 0.00889 850138088 noise
951769226 0.03348 850138088 noise
951769233 0.04309 850138130 good
951769238 0.01932 850138136 noise
951769246 0.14777 850138132 good
951769251 2.34118 850138132 good
951769259 0.10148 850138132 good
951769264 1.08802 850138148 good
951769272 0.02769 850138162 good
951769277 0.02108 850138164 good
951769284 0.45054 850138238 good
951769289 0.28851 850138270 good
951769295 3.27275 850138270 good
951769299 4.57933 850138272 good
951769304 2.04729 850138274 good
951769309 1.31185 850138278 good
951769314 1.02519 850138276 good
951769319 0.83041 850138288 good
951769325 0.75714 850138292 good
951769330 1.10104 850138308 good
951769334 0.07223 850138308 good
951769339 0.3778 850138310 good
951769344 0.94873 850138314 good
951769351 0.25638 850138314 good
951769355 0.05136 850138322 good
951769362 0.04464 850138328 good
951769365 0.03141 850138340 good
951769371 0.25679 850138344 good
951769377 0.16978 850138394 noise
951769383 0.08019 850137838 good
951769390 0.21091 850138000 good
951769395 0.03947 850137998 good
951769401 0.16813 850138088 noise
951769406 0.0434 850138088 noise
951769412 0.05704 850138088 noise
951769418 0.01963 850138088 noise
951769424 0.15046 850138324 good
951769429 0.03513 850138324 good
951769435 0.07027 850138340 good
951769443 0.09135 850138002 good
951769448 0.04681 850138002 good
951769456 0.04392 850138088 noise
951769462 0.00827 850138088 noise
951769470 0.07368 850138088 noise
951769475 0.05043 850138088 noise
951769482 3.38115 850138164 good
951769487 0.26702 850138192 noise
951769493 0.40022 850138230 good
951769500 0.06045 850138322 good
951769506 0.05539 850138088 noise
951769514 0.02098 850138088 noise
951769521 0.0371 850138136 noise
951769527 0.01674 850138088 noise
951769538 0.01116 850138088 noise
951769546 0.14694 850138322 good
951769554 0.07172 850138088 noise
951769645 1.43048 850140490 good
951769654 2.99788 850140498 good
951769662 33.2358 850140500 good
951769668 19.8743 850140500 good
951769674 0.00413 850140500 noise
951769681 3.13717 850140504 good
951769688 3.78963 850140506 good
951769694 30.0669 850140506 good
951769698 37.0382 850140508 good
951769706 2.10733 850140508 good
951769711 1.39586 850140510 good
951769718 0.04795 850140510 good
951769724 1.20748 850140512 good
951769730 1.56461 850140516 good
951769737 0.54086 850140514 good
951769744 11.9715 850140514 good
951769751 1.9887 850140516 good
951769758 1.55376 850140518 good
951769764 3.96613 850140522 good
951769771 51.3402 850140522 good
951769776 1.74369 850140522 good
951769784 0.36385 850140526 good
951769790 32.9643 850140528 good
951769797 1.20262 850140530 good
951769803 25.6825 850140528 good
951769808 45.8666 850140532 good
951769813 0.51606 850140532 good
951769818 12.9885 850140534 good
951769822 0.05198 850140536 good
951769826 38.6449 850140540 good
951769833 33.3518 850140542 good
951769839 0.30897 850140544 good
951769846 2.36701 850140546 noise
951769857 6.66723 850140548 good
951769864 4.09944 850140548 noise
951769870 1.66247 850140548 good
951769875 3.81971 850140548 good
951769878 27.2155 850140550 good
951769883 2.62452 850140550 good
951769890 25.5366 850140552 good
951769898 25.2519 850140552 good
951769905 20.452 850140552 good
951769911 2.5649 850140554 noise
951769917 0.6165 850140556 good
951769923 47.8529 850140562 good
951769930 6.53403 850140562 good
951769935 3.4045 850140562 noise
951769941 33.4774 850140564 good
951769948 39.7706 850140566 good
951769953 0.00682 850140566 good
951769959 8.49503 850140574 good
951769966 0.20957 850140570 noise
951769971 1.13907 850140570 good
951769978 35.3371 850140570 good
951769985 10.3165 850140578 good
951769992 0.37335 850140572 good
951769999 2.20922 850140574 noise
951770005 5.12298 850140574 good
951770012 4.62014 850140578 noise
951770018 13.4504 850140580 good
951770024 9.66686 850140584 good
951770031 1.18785 850140582 good
951770036 41.438 850140582 good
951770042 3.69715 850140584 good
951770049 19.4763 850140584 noise
951770053 8.94733 850140584 good
951770058 0.70961 850140586 noise
951770063 13.2811 850140588 good
951770068 38.2703 850140588 good
951770072 2.30067 850140594 good
951770077 0.30856 850140594 good
951770082 2.02931 850140590 good
951770087 0.0124 850140594 noise
951770091 1.88815 850140594 good
951770093 46.1365 850140594 good
951770098 0.03224 850140594 good
951770102 0.0094 850140594 noise
951770105 0.01529 850140594 good
951770111 0.24811 850140594 good
951770116 0.01416 850140594 noise
951770121 0.01157 850140594 noise
951770127 0.02253 850140594 good
951770132 2.404 850140588 good
951770136 0.5267 850140588 good
951770142 2.90952 850140598 good
951770147 2.11745 850140600 good
951770154 10.0171 850140600 good
951770159 0.18766 850140602 good
951770164 5.28366 850140602 noise
951770170 17.817 850140602 good
951770178 3.51083 850140604 noise
951770183 6.9079 850140610 good
951770188 35.2797 850140610 good
951770196 8.93566 850140610 good
951770200 4.70416 850140616 good
951770205 6.16409 850140616 good
951770210 0.75301 850140616 good
951770214 5.3033 850140618 good
951770220 28.654 850140618 good
951770224 8.07962 850140620 good
951770229 2.06527 850140620 good
951770234 22.1688 850140620 good
951770238 5.75922 850140626 good
951770243 2.45495 850140624 good
951770248 0.73585 850140626 good
951770251 2.08718 850140626 noise
951770258 0.09435 850140626 noise
951770264 0.13196 850140626 good
951770270 0.02542 850140626 good
951770276 3.03642 850140628 good
951770283 13.0684 850140630 good
951770288 36.0112 850140634 good
951770295 7.37415 850140634 good
951770300 18.2104 850140634 good
951770307 0.15242 850140632 good
951770312 3.81661 850140648 good
951770315 12.5504 850140642 good
951770321 4.15937 850140642 good
951770327 2.71463 850140644 good
951770333 41.5639 850140652 good
951770340 3.59846 850140646 good
951770347 2.79255 850140650 good
951770353 0.00114 850140648 good
951770358 15.6871 850140644 good
951770366 4.55928 850140654 good
951770375 0.00434 850140654 good
951770379 0.68574 850140654 good
951770386 0.76241 850140656 good
951770391 0.38668 850140658 noise
951770397 0.05208 850140648 good
951770401 0.40373 850140658 noise
951770406 3.30272 850140660 good
951770412 4.56641 850140662 good
951770417 2.03014 850140666 good
951770423 40.8491 850140666 good
951770428 7.49309 850140666 good
951770434 42.6069 850140668 good
951770439 44.0604 850140668 good
951770446 9.16289 850140674 good
951770452 3.19711 850140674 good
951770457 6.71766 850140668 good
951770465 8.21706 850140676 good
951770470 8.14875 850140682 good
951770477 37.1047 850140680 good
951770484 5.17609 850140682 good
951770489 0.94955 850140682 good
951770497 0.73007 850140682 good
951770501 4.21404 850140690 good
951770508 1.8741 850140690 good
951770513 4.27707 850140690 good
951770519 0.70237 850140696 good
951770525 1.99056 850140700 good
951770530 0.0062 850140696 good
951770536 0.05177 850140702 good
951770542 0.19747 850140698 good
951770548 1.45735 850140698 good
951770556 0.10809 850140706 noise
951770561 1.84444 850140706 good
951770569 0.14798 850140706 noise
951770574 16.8392 850140714 noise
951770580 0.00765 850140714 noise
951770586 7.93485 850140714 good
951770592 1.68127 850140722 good
951770599 0.13227 850140722 good
951770604 5.58602 850140726 good
951770610 0.3222 850140730 good
951770618 0.14901 850140732 good
951770623 0.16317 850140732 noise
951770630 0.05311 850140732 noise
951770636 1.18382 850140766 noise
951770641 1.42738 850140810 noise
951770647 2.63909 850140818 noise
951770653 0.93426 850140814 noise
951770658 3.0141 850140814 noise
951770663 21.2313 850140826 noise
951770670 1.88836 850140834 noise
951770674 2.97886 850140824 noise
951770680 0.01767 850140838 good
951770685 0.08742 850140824 noise
951770691 0.94656 850140826 good
951770696 0.0744 850140826 good
951770704 0.95203 850140826 noise
951770708 1.23135 850140828 good
951770714 1.40785 850140828 good
951770720 12.3374 850140832 good
951770728 13.9405 850140842 good
951770735 1.29015 850140842 noise
951770742 3.76835 850140850 good
951770748 1.0222 850140850 good
951770755 7.26544 850140852 good
951770760 0.29544 850140838 noise
951770768 0.5141 850140838 noise
951770773 11.2351 850140862 noise
951770780 3.64 850140862 good
951770785 3.57532 850140862 noise
951770791 0.00537 850140858 noise
951770795 1.7439 850140862 noise
951770802 0.4058 850140882 noise
951770808 0.29275 850140882 noise
951770814 2.82355 850140862 noise
951770822 5.15015 850140878 noise
951770828 2.51685 850140882 noise
951770834 9.90298 850140882 noise
951770842 3.29125 850140904 noise
951770847 0.00434 850140904 good
951770854 1.60326 850140930 noise
951770860 2.06372 850140922 good
951770867 2.47717 850140926 noise
951770873 3.86228 850140930 good
951770880 0.34214 850140938 noise
951770886 1.24447 850140938 noise
951770891 3.36224 850140938 noise
951770896 4.17508 850140940 noise
951770901 2.79089 850140952 noise
951770908 0.65711 850140954 good
951770914 2.69304 850140954 noise
951770921 2.56759 850140958 noise
951770928 3.41143 850140962 good
951770943 0.82007 850140968 noise
951770949 7.27515 850140968 good
951770955 3.869 850140970 good
951770960 3.89628 850140976 good
951770965 2.26109 850140984 good
951770969 0.96547 850140994 noise
951770976 5.17216 850140986 good
951770981 3.4756 850140978 good
951770987 3.96231 850140972 good
951770994 7.32072 850140980 good
951771000 1.40661 850140976 noise
951771005 4.06492 850140986 good
951771013 5.3747 850140986 good
951771018 1.93496 850140986 good
951771024 8.65086 850140986 good
951771032 6.05693 850140994 good
951771038 1.6262 850140994 noise
951771043 1.92535 850140994 good
951771050 10.1953 850140990 good
951771057 5.83796 850140990 good
951771064 14.5114 850140994 good
951771069 2.92957 850140992 good
951771077 0.01912 850140992 good
951771083 3.73104 850140994 good
951771089 1.26979 850140994 good
951771095 3.76111 850140994 noise
951771103 4.8884 850140994 good
951771110 5.96702 850140994 good
951771115 0.84911 850140994 good
951771121 3.54969 850140996 good
951771128 6.16161 850140996 good
951771135 3.06256 850140996 good
951771142 4.31344 850140996 good
951771148 2.52987 850140996 good
951771155 0.56235 850140996 good
951771161 8.70253 850140996 good
951771167 7.51086 850140996 good
951771174 9.14336 850140996 good
951771180 7.4625 850140996 good
951771188 3.9774 850140996 good
951771194 0.02645 850140996 noise
951771199 7.97298 850140998 good
951771206 2.36866 850140994 good
951771211 5.55864 850140998 good
951771218 0.38296 850140998 good
951771224 7.28487 850140998 good
951771229 2.20705 850140998 good
951771234 1.37302 850141000 good
951771239 2.48233 850141000 good
951771246 1.51552 850141000 good
951771252 0.91514 850140998 noise
951771257 0.14436 850141002 noise
951771263 5.93799 850140994 good
951771270 0.87722 850141002 noise
951771276 0.47348 850140998 noise
951771283 3.91767 850141002 good
951771288 23.3667 850141004 good
951771294 1.09433 850141004 good
951771300 1.47967 850140998 noise
951771307 1.63054 850141002 noise
951771313 24.9118 850141012 good
951771320 6.55645 850141018 good
951771326 3.15164 850141018 good
951771331 7.01433 850141018 good
951771338 2.82262 850141020 good
951771344 1.48122 850141024 noise
951771349 0.00496 850141024 good
951771357 0.39929 850141026 good
951771362 2.05752 850141026 noise
951771368 5.53353 850141036 good
951771374 7.31979 850141036 good
951771381 2.6857 850141040 noise
951771387 16.6017 850141042 good
951771393 1.57887 850141042 good
951771400 1.9175 850141044 good
951771405 5.89996 850141044 good
951771412 1.98229 850141044 good
951771418 3.86786 850141044 good
951771425 0.40549 850141044 good
951771431 5.86503 850141044 good
951771438 4.19388 850141046 good
951771443 1.38098 850141046 good
951771449 1.79143 850141046 good
951771453 3.01431 850141050 good
951771458 1.86583 850141044 good
951771465 0.02914 850141050 noise
951771471 0.03493 850141048 noise
951771477 0.35723 850141052 good
951771483 0.86812 850141052 good
951771488 2.25034 850141062 good
951771494 1.36796 850141054 good
951771499 1.9794 850141066 good
951771507 2.54867 850141058 good
951771512 4.34724 850141058 good
951771517 3.91891 850141058 noise
951771522 4.67925 850141060 good
951771528 0.57196 850141060 good
951771533 0.68016 850141064 good
951771538 2.74791 850141066 good
951771543 2.02022 850141066 good
951771547 4.78693 850141066 good
951771552 2.32061 850141068 noise
951771558 6.86873 850141068 good
951771563 0.11915 850141068 good
951771568 0.00651 850141068 good
951771572 2.39574 850141074 good
951771577 3.0018 850141074 good
951771583 5.8083 850141076 good
951771588 5.41314 850141076 good
951771594 3.27368 850141078 good
951771601 5.52867 850141080 good
951771607 1.00194 850141080 good
951771613 4.61436 850141082 good
951771620 6.89674 850141082 good
951771626 1.36703 850141084 good
951771633 2.41093 850141084 good
951771639 11.5399 850141084 good
951771645 4.6558 850141084 good
951771652 5.98996 850141086 good
951771658 11.5414 850141086 good
951771665 8.46951 850141090 good
951771670 13.1894 850141088 good
951771676 9.0145 850141088 good
951771684 18.1031 850141090 good
951771690 10.0666 850141090 good
951771697 5.62436 850141092 good
951771701 7.59312 850141092 good
951771706 2.95881 850141092 good
951771712 19.8755 850141098 good
951771718 2.07374 850141098 good
951771724 8.25695 850141098 good
951771730 4.56145 850141096 good
951771735 14.1265 850141102 good
951771742 4.94235 850141102 good
951771747 6.43018 850141104 good
951771753 1.40289 850141104 good
951771759 0.84095 850141104 good
951771764 0.37914 850141104 good
951771771 2.218 850141106 good
951771777 3.94567 850141106 good
951771782 9.33443 850141106 good
951771788 3.70903 850141106 noise
951771794 2.83161 850141108 good
951771800 3.41215 850141108 good
951771806 3.12219 850141108 good
951771813 1.75506 850141112 good
951771818 3.30881 850141106 good
951771824 6.21451 850141114 good
951771831 2.3697 850141114 good
951771837 3.87396 850141108 noise
951771844 2.08521 850141116 good
951771850 3.78664 850141118 good
951771856 1.62589 850141122 good
951771862 2.99746 850141122 good
951771866 0.01044 850141124 good
951771872 1.64263 850141126 good
951771878 4.61539 850141132 good
951771885 4.81121 850141132 good
951771892 0.48216 850141132 noise
951771898 21.6197 850141136 good
951771904 3.51838 850141138 noise
951771910 12.4171 850141138 good
951771918 8.58276 850141138 good
951771924 1.99087 850141138 noise
951771931 10.2836 850141146 good
951771938 2.95086 850141148 good
951771944 3.20909 850141198 noise
951771951 0.93333 850141198 noise
951771958 7.62329 850141198 noise
951771965 5.10593 850141198 noise
951771971 0.51761 850140516 good
951771979 0.03338 850140536 good
951771985 0.17319 850140566 noise
951771992 39.7843 850140586 good
951771998 0.24522 850140586 good
951772005 0.33904 850140602 good
951772012 0.12359 850140626 good
951772018 0.21732 850140648 good
951772026 33.3255 850140654 good
951772032 1.78823 850140648 good
951772037 0.07182 850140654 good
951772045 0.15562 850140696 good
951772049 0.10788 850140696 good
951772057 0.034 850140692 good
951772063 0.91008 850140698 good
951772073 0.28097 850140698 good
951772078 0.31662 850140722 good
951772083 0.86719 850140826 good
951772090 2.37993 850140850 good
951772095 0.09941 850141004 good
951772101 0.46284 850141074 good
951772107 0.80612 850141074 good
951772113 0.5328 850141108 good
951772119 0.14643 850141198 noise
951772125 0.06965 850140648 good
951772131 0.08639 850140692 good
951772137 0.05384 850140702 good
951772142 0.03472 850140696 good
951772147 0.61784 850140636 good
951772153 0.04557 850140826 good
951772159 0.24501 850140992 good
951772221 4.70457 850136298 good
951772227 3.72102 850136298 good
951772233 4.29154 850136298 good
951772239 2.28093 850136298 noise
951772247 4.57168 850136298 noise
951772253 3.104 850136298 noise
951772260 3.12601 850136298 good
951772266 0.01395 850136298 good
951772273 9.67812 850136302 good
951772280 3.65292 850136298 good
951772286 5.45903 850136310 good
951772293 0.12597 850136308 good
951772298 6.74628 850136306 good
951772304 10.3528 850136306 good
951772310 1.77521 850136306 noise
951772316 10.7254 850136308 good
951772322 8.32804 850136308 good
951772328 6.40651 850136308 good
951772334 18.4867 850136308 good
951772340 5.77689 850136308 noise
951772344 0.73565 850136308 noise
951772351 2.77353 850136308 good
951772355 15.4752 850136312 good
951772361 15.1415 850136314 good
951772367 13.1557 850136314 good
951772373 9.70323 850136314 good
951772379 7.98435 850136314 good
951772385 12.4186 850136314 good
951772391 3.13418 850136316 good
951772397 11.6179 850136308 good
951772402 11.3955 850136316 good
951772407 2.20756 850136316 noise
951772413 10.3179 850136320 good
951772419 1.6946 850136324 good
951772428 10.7328 850136322 good
951772434 12.0966 850136322 good
951772441 5.97333 850136322 good
951772448 0.38296 850136322 good
951772455 18.6347 850136324 good
951772462 8.74727 850136324 good
951772468 1.84847 850136328 noise
951772475 9.45988 850136330 good
951772482 7.84856 850136326 good
951772489 0.06582 850136328 good
951772495 11.0722 850136330 good
951772502 2.96905 850136330 good
951772509 17.9442 850136330 good
951772515 3.88615 850136330 noise
951772523 4.55339 850136330 noise
951772529 14.0161 850136330 good
951772535 6.00805 850136332 good
951772541 8.51777 850136332 good
951772548 8.34685 850136332 good
951772555 3.23121 850136328 good
951772561 0.59077 850136334 good
951772569 0.12566 850136330 noise
951772576 11.8787 850136332 good
951772581 4.21889 850136330 good
951772589 7.18174 850136330 good
951772595 3.95766 850136338 good
951772600 8.49968 850136338 good
951772606 1.89136 850136338 good
951772612 15.3178 850136332 good
951772618 8.75554 850136340 good
951772623 4.32357 850136340 good
951772630 2.79782 850136340 good
951772635 7.88483 850136342 good
951772640 19.2235 850136342 good
951772647 11.4084 850136344 good
951772653 8.2618 850136344 good
951772659 15.0126 850136346 good
951772665 4.13767 850136348 good
951772671 7.32217 850136346 good
951772678 2.33477 850136346 good
951772685 4.5414 850136346 good
951772690 14.0128 850136348 good
951772696 10.392 850136348 good
951772703 0.6567 850136348 good
951772710 1.17059 850136348 noise
951772716 0.26392 850136348 noise
951772723 14.0084 850136350 good
951772728 2.47551 850136350 noise
951772734 6.73936 850136348 good
951772739 9.04798 850136352 good
951772745 13.1074 850136354 good
951772751 13.2988 850136354 good
951772757 11.6707 850136354 good
951772761 13.112 850136356 good
951772766 16.3706 850136356 good
951772774 0.82658 850136356 good
951772782 0.01033 850136356 good
951772789 6.37034 850136360 good
951772795 8.44626 850136360 good
951772802 5.88198 850136360 good
951772809 7.97732 850136362 noise
951772815 2.64416 850136362 good
951772822 7.36898 850136362 good
951772829 0.13041 850136362 noise
951772835 17.3807 850136364 good
951772842 7.26906 850136364 good
951772849 8.62214 850136364 good
951772855 1.47367 850136364 noise
951772864 4.52611 850136366 good
951772870 1.61958 850136366 good
951772876 8.47416 850136370 good
951772884 12.4035 850136370 good
951772890 0.17412 850136370 good
951772896 1.20283 850136378 good
951772900 0.94242 850136370 good
951772906 22.9855 850136370 good
951772914 1.54022 850136370 noise
951772920 1.10528 850136370 noise
951772926 9.69156 850136372 good
951772932 12.5661 850136372 good
951772938 8.21799 850136372 good
951772945 8.04211 850136376 good
951772952 7.12284 850136372 good
951772958 8.39697 850136378 good
951772963 5.69318 850136374 good
951772969 15.0003 850136378 good
951772975 18.025 850136378 good
951772981 8.63671 850136378 noise
951772987 9.09717 850136378 good
951772993 1.1494 850136378 good
951773000 14.0709 850136378 good
951773011 4.41874 850136378 good
951773018 3.55971 850136380 good
951773024 0.77678 850136376 good
951773030 5.0059 850136376 good
951773035 11.9163 850136384 good
951773043 15.1822 850136386 good
951773049 6.09082 850136386 good
951773054 1.77428 850136378 good
951773061 6.19881 850136394 good
951773069 11.9444 850136388 good
951773075 11.032 850136388 good
951773083 15.5343 850136390 good
951773089 10.2341 850136390 good
951773096 19.8385 850136392 good
951773103 14.4526 850136392 good
951773110 10.6374 850136394 good
951773117 5.88622 850136396 good
951773123 5.89552 850136396 good
951773131 3.35097 850136396 good
951773137 9.55154 850136394 good
951773144 45.8654 850136398 good
951773151 5.87702 850136398 good
951773158 1.78802 850136400 good
951773164 6.55614 850136400 good
951773171 20.5879 850136402 good
951773178 7.93516 850136402 good
951773184 7.36464 850136404 good
951773189 5.8487 850136404 good
951773195 12.4258 850136410 good
951773200 7.92534 850136408 good
951773205 2.09927 850136406 good
951773211 24.5946 850136408 good
951773216 8.96087 850136410 good
951773222 2.38499 850136410 good
951773227 28.6015 850136410 good
951773233 27.4672 850136410 good
951773238 21.7692 850136410 good
951773242 2.26584 850136412 good
951773246 7.70462 850136414 good
951773251 5.49767 850136414 good
951773257 16.671 850136416 good
951773262 13.6102 850136418 good
951773268 5.20575 850136418 good
951773273 7.88153 850136418 good
951773278 3.29879 850136420 good
951773284 5.82824 850136426 good
951773289 21.2072 850136426 good
951773295 0.88755 850136426 noise
951773300 17.8141 850136428 good
951773305 0.66001 850136434 good
951773310 0.00909 850136436 noise
951773315 4.69124 850136442 good
951773320 11.3156 850136442 good
951773325 4.03867 850136442 good
951773332 3.75285 850136444 good
951773337 10.0735 850136444 good
951773342 11.6127 850136444 good
951773346 2.5774 850136448 noise
951773350 1.16966 850136448 noise
951773356 2.28124 850136448 noise
951773361 6.95708 850136450 good
951773368 6.06116 850136450 good
951773373 9.64351 850136452 good
951773378 6.23911 850136452 noise
951773384 14.4246 850136452 good
951773389 9.8353 850136452 good
951773395 9.01181 850136452 good
951773401 5.89521 850136454 good
951773407 17.2197 850136458 good
951773412 5.74992 850136460 good
951773418 7.05133 850136460 good
951773423 9.72349 850136460 good
951773429 2.03365 850136460 good
951773435 5.71612 850136460 good
951773441 10.7019 850136462 good
951773446 6.60864 850136462 good
951773452 6.75145 850136460 good
951773458 8.26149 850136464 good
951773463 6.89054 850136466 good
951773469 0.52939 850136466 good
951773474 12.0999 850136468 good
951773480 8.47023 850136468 good
951773485 17.9799 850136468 good
951773490 0.04381 850136468 noise
951773496 5.71054 850136470 good
951773501 10.275 850136470 good
951773507 11.7831 850136470 good
951773513 14.1525 850136472 good
951773518 11.593 850136474 good
951773523 4.68132 850136474 good
951773533 7.15776 850136474 good
951773538 10.1507 850136476 good
951773542 4.49346 850136476 good
951773548 0.31176 850136476 good
951773553 8.24196 850136476 good
951773560 0.00176 850136476 good
951773565 13.1914 850136484 good
951773570 0.0032 850136484 good
951773577 8.17376 850136482 good
951773582 3.94536 850136482 good
951773587 10.9628 850136482 good
951773594 10.7748 850136482 good
951773599 0.00837 850136482 noise
951773605 6.66568 850136484 good
951773611 11.5895 850136484 good
951773616 2.00193 850136484 good
951773622 11.3103 850136486 good
951773628 3.25208 850136486 good
951773633 1.76239 850136486 good
951773638 9.19493 850136490 good
951773644 8.98805 850136492 good
951773650 10.012 850136492 good
951773656 8.05689 850136494 good
951773662 7.08966 850136494 good
951773667 2.58474 850136498 good
951773673 11.9129 850136498 good
951773678 14.7664 850136498 good
951773683 19.4405 850136498 good
951773690 12.8355 850136500 good
951773696 15.4212 850136500 good
951773701 4.61828 850136506 good
951773706 7.06538 850136506 good
951773713 10.5483 850136508 good
951773718 3.08065 850136510 good
951773724 0.01044 850136510 good
951773730 13.4889 850136514 good
951773735 1.32249 850136484 noise
951773741 10.9077 850136596 good
951773747 5.22662 850136602 noise
951773752 2.11353 850136606 noise
951773758 7.64623 850136606 good
951773765 1.74875 850136608 noise
951773770 4.37545 850136618 good
951773775 4.7428 850136618 good
951773780 2.17315 850136618 noise
951773786 0.03276 850136618 good
951773792 12.5212 850136620 good
951773797 2.61564 850136620 noise
951773803 22.0037 850136620 good
951773808 4.94266 850136620 good
951773813 2.64488 850136620 good
951773819 1.51129 850136620 good
951773824 0.10819 850136622 good
951773832 0.97198 850136630 good
951773838 15.3389 850136626 good
951773843 0.53187 850136626 good
951773849 2.82396 850136626 noise
951773853 0.13124 850136626 noise
951773856 1.28798 850136626 noise
951773862 0.02532 850136626 noise
951773869 9.21497 850136634 good
951773874 0.24201 850136626 noise
951773879 0.00424 850136626 good
951773886 0.02842 850136628 good
951773892 0.20161 850136628 good
951773897 0.03121 850136634 noise
951773903 32.447 850136636 noise
951773908 3.27905 850136636 good
951773914 20.7261 850136634 good
951773920 0.06861 850136642 noise
951773926 0.04051 850136644 noise
951773929 0.00279 850136650 noise
951773931 13.1911 850136652 good
951773933 26.4001 850136652 good
951773935 15.1065 850136658 good
951773937 0.71911 850136648 noise
951773940 2.06093 850136660 good
951773943 1.61855 850136668 noise
951773945 5.53167 850136680 noise
951773948 11.6486 850136676 noise
951773950 6.02014 850136676 good
951773956 2.38127 850136680 noise
951773960 1.28632 850136680 noise
951773965 4.68432 850136692 good
951773969 3.59402 850136680 noise
951773973 2.29695 850136696 noise
951773977 2.75359 850136694 noise
951773982 12.0485 850136700 good
951773986 8.86012 850136708 good
951773990 2.37032 850136708 good
951773994 4.72214 850136716 good
951774002 2.18173 850136716 good
951774008 3.6709 850136724 good
951774013 4.5722 850136732 noise
951774019 3.26014 850136732 good
951774024 4.29412 850136732 good
951774030 7.90808 850136732 good
951774035 1.57298 850136736 good
951774039 10.0113 850136740 good
951774044 5.67055 850136740 good
951774049 3.17148 850136740 good
951774054 0.59067 850136746 good
951774059 45.3328 850136748 good
951774065 0.12969 850136748 good
951774070 4.59214 850136748 good
951774075 0.10881 850136752 good
951774082 1.11096 850136754 good
951774086 2.80422 850136762 good
951774091 3.19235 850136756 good
951774097 22.7047 850136756 good
951774103 1.08368 850136756 good
951774108 7.15993 850136756 good
951774113 0.09548 850136756 good
951774118 3.24485 850136756 good
951774124 0.6009 850136756 good
951774130 6.34275 850136756 good
951774134 0.76086 850136756 good
951774140 0.20202 850136756 good
951774145 0.43752 850136758 good
951774150 6.21327 850136758 good
951774156 0.01261 850136756 good
951774161 0.01891 850136760 good
951774166 6.77511 850136760 good
951774172 4.30187 850136760 good
951774176 1.91233 850136760 good
951774180 0.02046 850136760 good
951774186 1.58507 850136762 noise
951774192 1.27031 850136762 good
951774197 14.1142 850136762 good
951774203 2.40617 850136764 good
951774208 2.43108 850136764 good
951774213 8.71751 850136764 good
951774220 2.89175 850136766 good
951774225 3.53119 850136768 good
951774231 6.2483 850136768 good
951774237 0.16988 850136770 good
951774242 4.82031 850136770 good
951774247 24.9531 850136770 good
951774253 4.07505 850136770 good
951774258 0.63655 850136770 good
951774264 4.27221 850136764 good
951774269 1.69915 850136774 good
951774275 3.28319 850136774 good
951774280 0.91483 850136770 noise
951774286 7.29623 850136774 noise
951774290 3.97678 850136774 noise
951774295 2.4254 850136770 good
951774299 0.01147 850136770 noise
951774304 7.5027 850136778 good
951774308 13.8395 850136788 good
951774313 3.97595 850136788 good
951774318 4.31592 850136794 good
951774322 10.2349 850136794 good
951774327 5.38824 850136794 good
951774331 6.53475 850136794 good
951774337 30.3643 850136802 good
951774341 2.66141 850136808 good
951774347 1.14579 850136832 noise
951774352 1.91512 850136828 good
951774357 1.55748 850136828 noise
951774362 2.41196 850136828 noise
951774364 3.73487 850136834 good
951774368 4.57788 850136834 good
951774374 4.24442 850136842 good
951774380 5.31932 850136836 good
951774386 0.46253 850136832 noise
951774393 3.09356 850136834 good
951774401 2.91841 850136842 good
951774407 2.73168 850136850 good
951774414 2.32144 850136844 good
951774420 4.20411 850136844 good
951774427 2.8065 850136844 good
951774433 9.01998 850136848 noise
951774439 2.68983 850136850 good
951774448 10.3982 850136850 good
951774454 2.77147 850136852 good
951774461 1.37426 850136854 good
951774466 1.02964 850136832 noise
951774473 3.55062 850136860 good
951774479 3.90702 850136862 good
951774484 2.11404 850136862 noise
951774491 1.71424 850136862 good
951774502 6.93642 850136868 noise
951774507 2.62225 850136860 good
951774513 0.66073 850136868 noise
951774520 17.2249 850136870 good
951774527 0.80592 850136870 good
951774533 0.02645 850136866 good
951774538 0.09207 850136872 noise
951774544 0.11501 850136872 noise
951774549 1.59003 850136872 good
951774555 0.01447 850136874 good
951774562 2.70048 850136876 good
951774567 2.73571 850136882 good
951774572 2.62421 850136880 good
951774576 3.32142 850136880 good
951774582 1.86366 850136882 good
951774588 10.9189 850136884 good
951774592 18.9308 850136880 good
951774598 3.77403 850136884 noise
951774603 5.37553 850136884 good
951774609 1.08079 850136884 good
951774614 9.83375 850136886 good
951774620 8.5343 850136888 good
951774625 2.47717 850136890 good
951774631 8.54856 850136892 good
951774636 17.9195 850136892 good
951774641 0.00083 850136884 good
951774648 13.007 850136898 good
951774653 11.9066 850136906 good
951774659 7.84381 850136900 good
951774664 9.02308 850136900 good
951774670 2.4595 850136900 good
951774676 8.36369 850136906 good
951774682 3.01792 850136906 good
951774686 2.36773 850136906 good
951774692 5.19159 850136908 good
951774697 3.62357 850136908 good
951774704 2.26626 850136906 good
951774708 2.1035 850136906 good
951774713 3.15867 850136906 good
951774719 2.25675 850136908 good
951774724 4.8387 850136906 noise
951774730 15.427 850136912 good
951774736 8.75523 850136914 good
951774741 1.59148 850136914 good
951774745 4.33163 850136916 good
951774752 7.80909 850136922 good
951774757 1.71279 850136916 good
951774761 2.3604 850136914 good
951774768 3.21633 850136914 good
951774772 1.79246 850136922 good
951774777 5.85552 850136922 good
951774783 1.22463 850136922 good
951774785 3.60363 850136922 good
951774791 3.0265 850136926 noise
951774796 2.2892 850136928 good
951774800 1.44009 850136926 noise
951774806 3.8847 850136928 good
951774812 0.85417 850136930 good
951774817 1.44153 850136940 good
951774823 0.06531 850136932 noise
951774827 0.51503 850136938 good
951774832 0.86151 850136936 good
951774838 0.71219 850136938 good
951774845 5.84715 850136942 good
951774850 1.69874 850136946 good
951774856 3.67338 850136938 noise
951774862 2.26429 850136938 noise
951774866 2.56294 850136946 noise
951774872 3.04841 850136952 good
951774878 3.83149 850136956 good
951774884 0.12938 850136962 good
951774890 0.00176 850136988 noise
951774895 8.19463 850136998 noise
951774900 2.1871 850137006 noise
951774906 0.01126 850136992 noise
951774913 2.63393 850136992 noise
951774918 0.81625 850137002 noise
951774924 0.00496 850136298 good
951774930 8.73084 850136330 good
951774934 21.6061 850136340 good
951774941 0.55357 850136370 good
951774947 6.24169 850136430 good
951774952 10.4657 850136466 good
951774958 9.37008 850136476 good
951774963 3.82084 850136508 good
951774969 0.28262 850136510 good
951774975 0.0279 850136618 good
951774982 0.05735 850136618 good
951774988 0.00372 850136622 good
951774995 0.30174 850136628 good
951775003 0.02325 850136628 good
951775009 0.07079 850136770 good
951775014 0.07823 850136778 good
951775020 0.50676 850136834 good
951775028 0.01891 850136870 good
951775033 0.43236 850136866 good
951775039 0.07451 850136866 good
951775044 0.03813 850136866 good
951775051 0.21969 850136874 good
951775057 0.85789 850136900 good
951775065 2.42664 850136924 good
951775073 0.41376 850136962 good
951775080 0.1362 850137002 noise
951775086 0.01912 850136628 good
951775092 0.03048 850136874 good
951775099 0.01653 850136484 good
951775105 0.0124 850136484 good
951775110 0.02656 850136760 good
951775116 0.26196 850136850 good
951775173 5.91525 850139164 good
951775180 7.71454 850139164 good
951775184 3.89483 850139168 good
951775192 9.07888 850139164 good
951775198 3.91622 850139168 good
951775206 8.11248 850139168 good
951775212 2.37393 850139170 good
951775218 8.28102 850139170 good
951775223 7.29561 850139172 good
951775230 5.32149 850139172 good
951775236 8.77363 850139172 good
951775243 4.58635 850139172 good
951775249 2.43449 850139174 good
951775254 4.44902 850139174 good
951775260 5.00383 850139174 good
951775265 4.27996 850139178 good
951775271 10.4868 850139178 good
951775279 7.32362 850139180 good
951775285 11.3536 850139180 good
951775292 7.47914 850139180 good
951775297 3.22563 850139180 good
951775303 4.19481 850139180 good
951775309 10.7328 850139182 good
951775314 7.63786 850139182 good
951775321 5.68471 850139182 good
951775327 9.05005 850139184 good
951775333 4.2221 850139188 good
951775339 7.25025 850139188 good
951775345 2.67268 850139188 good
951775351 1.50984 850139190 good
951775355 3.66739 850139192 good
951775363 10.0034 850139190 good
951775369 4.31685 850139192 good
951775375 6.58642 850139196 good
951775380 11.8742 850139196 good
951775385 4.25516 850139196 good
951775392 12.3145 850139198 good
951775397 3.13004 850139198 good
951775403 2.64674 850139198 good
951775407 2.80278 850139190 good
951775412 11.3512 850139198 good
951775417 5.77244 850139204 good
951775423 3.63814 850139202 good
951775429 8.45359 850139204 good
951775435 0.12783 850139204 good
951775441 15.7157 850139204 good
951775448 5.67954 850139204 good
951775453 2.09172 850139206 noise
951775465 3.09677 850139206 good
951775472 1.61307 850139206 good
951775477 4.29391 850139202 good
951775484 2.01732 850139210 good
951775489 2.53524 850139210 good
951775496 3.5313 850139210 good
951775502 8.72495 850139212 good
951775508 0.58591 850139212 good
951775515 7.21904 850139214 good
951775522 4.06905 850139216 good
951775529 9.18253 850139216 good
951775535 4.03723 850139216 good
951775542 0.60586 850139216 noise
951775550 12.0122 850139218 good
951775556 17.1874 850139218 good
951775561 0.58271 850139218 good
951775569 7.29985 850139218 good
951775576 6.64046 850139216 good
951775582 11.2056 850139220 good
951775589 3.70862 850139220 good
951775595 8.77259 850139222 good
951775602 0.10995 850139226 good
951775607 8.06443 850139230 good
951775614 6.70484 850139228 good
951775620 5.07875 850139228 good
951775627 0.02242 850139230 good
951775633 11.1431 850139236 good
951775639 5.2942 850139236 good
951775645 6.28933 850139230 good
951775648 11.3501 850139238 good
951775655 4.79406 850139242 good
951775660 9.35944 850139240 good
951775666 11.0597 850139240 good
951775671 8.41691 850139240 good
951775678 3.69808 850139242 good
951775684 2.12748 850139248 good
951775689 13.6246 850139248 good
951775695 1.63064 850139248 good
951775702 14.4631 850139248 good
951775708 15.7992 850139254 good
951775714 3.70376 850139254 good
951775720 5.57476 850139260 good
951775726 9.92344 850139260 good
951775733 0.47348 850139262 good
951775738 1.0131 850139262 good
951775741 4.01666 850139264 good
951775745 9.23078 850139264 good
951775748 3.94433 850139264 good
951775751 6.06096 850139272 good
951775754 6.40713 850139274 good
951775759 4.98223 850139278 good
951775764 3.11888 850139276 good
951775770 12.4008 850139276 good
951775776 4.19047 850139276 good
951775782 4.02462 850139280 good
951775789 0.05745 850139280 good
951775795 9.85834 850139282 good
951775800 0.03658 850139282 good
951775806 4.49077 850139286 good
951775813 1.23269 850139282 good
951775819 0.663 850139294 good
951775826 7.01712 850139292 good
951775830 0.03823 850139296 good
951775836 1.6696 850139298 good
951775843 5.1145 850139298 good
951775849 1.22205 850139302 good
951775857 1.93197 850139302 good
951775863 2.86612 850139302 good
951775869 2.13171 850139306 good
951775875 6.9637 850139308 good
951775880 0.03751 850139308 good
951775885 0.56607 850139316 good
951775890 9.40997 850139316 good
951775897 7.1681 850139316 good
951775903 7.18907 850139316 noise
951775908 10.2125 850139318 good
951775915 7.01413 850139318 good
951775919 2.94631 850139322 good
951775927 6.76664 850139322 good
951775934 3.88078 850139324 good
951775940 4.93687 850139326 good
951775947 6.44878 850139332 good
951775954 1.10311 850139328 good
951775961 3.56591 850139332 good
951775967 3.97533 850139330 good
951775974 4.69145 850139334 good
951775980 6.49197 850139334 good
951775985 4.92654 850139336 good
951775990 4.2006 850139336 good
951776000 1.76766 850139606 noise
951776007 2.56934 850139338 noise
951776014 0.04764 850139336 noise
951776020 2.06269 850139340 good
951776024 3.81785 850139340 good
951776031 8.76536 850139342 good
951776037 10.8718 850139344 good
951776043 1.12409 850139348 good
951776049 4.25723 850139350 good
951776055 5.59956 850139350 good
951776061 2.47872 850139350 good
951776067 4.50431 850139350 good
951776074 4.13591 850139352 good
951776080 6.05755 850139352 good
951776085 3.87726 850139358 good
951776091 3.25219 850139358 good
951776096 3.20424 850139358 good
951776100 2.1993 850139360 good
951776106 0.33336 850139360 noise
951776112 1.66009 850139364 noise
951776117 28.7194 850139366 good
951776124 2.19186 850139362 good
951776129 0.12648 850139368 good
951776135 7.08915 850139372 good
951776142 6.08607 850139372 good
951776147 12.7011 850139374 good
951776152 1.01786 850139376 good
951776159 1.14196 850139384 good
951776165 2.34851 850139388 noise
951776170 1.31237 850139388 noise
951776176 0.01395 850139390 good
951776182 2.65387 850139400 good
951776188 7.58506 850139402 good
951776194 1.39235 850139436 noise
951776200 3.31594 850139476 noise
951776206 2.21232 850139476 noise
951776213 3.47467 850139488 good
951776217 1.15323 850139486 noise
951776225 2.83533 850139488 noise
951776231 1.63539 850139494 good
951776237 4.36801 850139496 good
951776243 0.02015 850139494 noise
951776249 0.1333 850139496 good
951776255 0.86006 850139496 good
951776262 1.76591 850139498 good
951776268 0.69349 850139498 good
951776273 2.10133 850139506 good
951776281 2.41527 850139502 good
951776286 5.27199 850139506 good
951776292 0.29006 850139510 good
951776299 2.34386 850139510 noise
951776306 3.13056 850139514 noise
951776311 0.47865 850139510 noise
951776317 2.72466 850139510 noise
951776323 0.41438 850139510 noise
951776329 0.17257 850139518 good
951776333 3.40068 850139518 noise
951776339 2.95179 850139520 good
951776345 5.67582 850139522 good
951776352 0.08835 850139526 noise
951776358 1.60532 850139510 noise
951776364 3.15164 850139540 noise
951776370 2.33405 850139544 noise
951776376 1.21916 850139510 noise
951776382 1.59633 850139510 noise
951776388 2.31338 850139544 noise
951776394 3.37784 850139544 noise
951776401 0.3811 850139544 noise
951776407 1.67166 850139546 good
951776412 2.13885 850139566 good
951776419 2.17935 850139542 noise
951776425 3.04179 850139580 good
951776431 25.9364 850139594 good
951776436 16.3894 850139594 good
951776442 0.89551 850139590 noise
951776449 0.88187 850139594 noise
951776455 4.70261 850139600 good
951776462 2.2024 850139602 noise
951776468 0.30908 850139604 noise
951776475 5.13217 850139606 good
951776480 0.34979 850139610 good
951776486 11.6435 850139610 good
951776493 3.33826 850139618 noise
951776499 2.7602 850139618 noise
951776505 1.7409 850139622 noise
951776512 3.64651 850139618 noise
951776518 1.70142 850139620 noise
951776524 0.23643 850139620 good
951776530 2.69469 850139618 noise
951776541 2.25727 850139620 noise
951776547 2.07664 850139630 noise
951776551 0.64513 850139624 good
951776556 3.84606 850139618 noise
951776563 2.90591 850139642 good
951776569 4.88251 850139630 good
951776576 0.00723 850139632 good
951776582 0.00858 850139630 noise
951776589 1.49506 850139632 good
951776595 0.3068 850139632 good
951776599 1.85973 850139652 noise
951776606 0.05828 850139652 noise
951776612 0.34556 850139652 noise
951776618 2.53968 850139638 good
951776624 9.47982 850139638 good
951776630 3.25229 850139638 good
951776636 3.49523 850139642 good
951776642 1.51511 850139642 noise
951776647 3.67679 850139642 noise
951776653 5.73586 850139654 noise
951776660 2.62494 850139642 good
951776666 1.85581 850139642 good
951776671 7.42644 850139642 good
951776677 0.02563 850139642 good
951776683 1.38026 850139648 good
951776690 0.38668 850139644 good
951776697 3.73518 850139644 good
951776703 5.1762 850139652 good
951776710 0.80106 850139648 good
951776716 4.67522 850139648 good
951776723 2.30098 850139650 good
951776731 0.20771 850139648 good
951776737 10.9451 850139652 good
951776743 11.8429 850139650 good
951776748 1.14434 850139654 good
951776753 5.10355 850139652 good
951776760 6.08576 850139652 good
951776767 16.1401 850139652 good
951776772 2.8405 850139652 good
951776776 3.27616 850139652 good
951776781 5.68213 850139652 noise
951776789 4.30807 850139652 good
951776794 1.27733 850139650 good
951776799 4.62221 850139656 good
951776806 3.71358 850139652 good
951776812 4.75965 850139658 good
951776818 5.79559 850139658 good
951776824 1.50478 850139660 good
951776832 4.22158 850139660 good
951776838 8.0572 850139660 good
951776845 0.01095 850139652 noise
951776852 2.96067 850139662 good
951776857 0.6226 850139662 good
951776864 3.84451 850139662 good
951776869 27.6137 850139658 good
951776877 4.8419 850139664 good
951776884 1.78947 850139664 good
951776888 4.99505 850139660 good
951776896 7.33798 850139668 good
951776902 1.86769 850139676 noise
951776909 4.72844 850139678 noise
951776914 1.52307 850139678 noise
951776922 7.57958 850139678 good
951776927 2.80154 850139678 good
951776932 1.71186 850139678 noise
951776939 8.60229 850139684 good
951776944 12.1399 850139688 good
951776950 0.62704 850139700 good
951776956 0.55915 850139700 noise
951776962 1.88547 850139700 noise
951776968 0.07606 850139700 noise
951776973 5.24429 850139710 good
951776980 0.49395 850139776 noise
951776985 2.14122 850139714 good
951776991 1.7595 850139716 good
951776998 15.5874 850139718 good
951777003 0.02139 850139720 good
951777009 2.26564 850139728 good
951777016 7.24705 850139724 good
951777021 6.45084 850139730 good
951777029 2.72641 850139724 good
951777034 0.00124 850139732 noise
951777040 1.73635 850139732 noise
951777046 3.54597 850139736 good
951777052 13.0328 850139736 good
951777058 0.75921 850139742 good
951777065 1.94437 850139742 good
951777071 1.55035 850139744 good
951777079 2.82437 850139746 good
951777092 4.38795 850139742 good
951777098 16.4999 850139750 good
951777105 1.70287 850139758 good
951777112 6.41085 850139762 good
951777117 4.244 850139764 good
951777123 7.17006 850139764 good
951777129 12.4829 850139764 good
951777136 9.09128 850139762 good
951777142 10.2364 850139766 good
951777148 5.99234 850139766 good
951777155 4.41244 850139766 good
951777162 5.94036 850139772 good
951777168 8.81382 850139772 good
951777175 4.78135 850139778 good
951777181 6.2388 850139778 good
951777188 9.04302 850139772 good
951777193 0.42626 850139776 noise
951777199 6.21296 850139778 good
951777205 2.5617 850139780 good
951777212 8.14979 850139778 good
951777218 8.29714 850139782 good
951777223 4.54461 850139786 good
951777227 5.30526 850139790 noise
951777232 4.30135 850139790 good
951777237 1.81179 850139790 good
951777243 0.69834 850139796 good
951777249 3.40781 850139798 good
951777257 1.51222 850139806 good
951777263 3.24774 850139806 good
951777270 1.99283 850139806 good
951777275 1.71165 850139808 noise
951777281 2.62432 850139808 good
951777287 3.70531 850139812 good
951777292 6.32219 850139812 good
951777298 2.21759 850139814 good
951777304 2.35492 850139816 good
951777310 0.00692 850139820 noise
951777315 0.85717 850139826 good
951777321 5.74124 850139864 noise
951777323 1.19601 850139868 noise
951777326 7.5492 850139868 noise
951777329 3.32462 850139168 good
951777333 2.34583 850139170 good
951777335 8.80669 850139196 good
951777339 6.94045 850139204 good
951777342 9.22283 850139212 good
951777345 3.64734 850139222 good
951777348 5.85966 850139226 good
951777351 2.74057 850139230 good
951777355 0.02976 850139240 good
951777360 3.54401 850139262 good
951777366 2.21697 850139280 good
951777371 2.06393 850139286 good
951777377 0.0216 850139294 good
951777384 1.97764 850139300 good
951777389 4.77825 850139306 good
951777395 2.48264 850139308 good
951777401 0.57599 850139316 good
951777406 9.18087 850139324 good
951777413 0.03513 850139338 good
951777419 3.67266 850139340 good
951777424 1.44453 850139340 good
951777430 3.33051 850139348 good
951777437 0.24656 850139350 good
951777442 0.98799 850139368 good
951777448 1.35814 850139388 good
951777455 0.37707 850139390 good
951777462 0.18022 850139488 good
951777468 0.05012 850139496 good
951777474 0.03069 850139518 good
951777480 0.06975 850139518 good
951777485 0.40177 850139526 noise
951777492 0.04919 850139632 good
951777499 0.24739 850139652 noise
951777504 0.42574 850139642 good
951777511 0.13516 850139642 good
951777517 0.09641 850139642 good
951777523 1.61256 850139650 good
951777528 0.82524 850139728 noise
951777534 0.03792 850139720 good
951777540 0.1177 850139742 good
951777548 0.20078 850139864 noise
951777553 2.35957 850139294 good
951777559 0.02108 850139336 good
951777565 0.08143 850139526 noise
951777571 0.20088 850139738 good
951777576 0.01085 850139338 good
951777582 0.1457 850139622 good
951777593 0.0464 850139620 good
951777600 0.0621 850139642 good
Here we do not have the brain area information but we need it, so we need to do some preprocessing to extract brain area from the nwb object using the peak_channel_id metadata. Luckily, Pynapple stored the nwb object as well.
# Units and brain areas those units belong to are in two different places.
# With the electrodes table, we can map units to their corresponding brain regions.
def get_unit_location(unit_id):
"""Aligns location information from electrodes table with channel id from the units table
"""
return channel_probes[int(units[unit_id].peak_channel_id)]
channel_probes = {}
electrodes = nwb.electrodes
for i in range(len(electrodes)):
channel_id = electrodes["id"][i]
location = electrodes["location"][i]
channel_probes[channel_id] = location
# Add a new column to include location in our spikes TsGroup
units.brain_area = [channel_probes[int(ch_id)] for ch_id in units.peak_channel_id]
# Remove peak_channel_id because we already got the brain_area information
units.drop_info("peak_channel_id")
print(units)
Index rate quality brain_area
--------- -------- --------- ------------
951763702 2.38003 good PoT
951763707 0.01147 noise PoT
951763711 3.1503 good PoT
951763715 6.53 good PoT
951763720 2.00296 good PoT
951763724 8.66233 noise PoT
951763729 11.134 noise PoT
951763733 23.8915 good PoT
951763737 1.01848 noise PoT
951763741 11.8133 noise PoT
951763745 13.4006 noise PoT
951763749 18.2252 noise PoT
951763753 18.9817 noise PoT
951763758 13.2587 noise PoT
951763762 17.3762 noise PoT
951763766 12.0932 noise PoT
951763770 4.00705 noise LP
951763774 5.77131 good PoT
951763778 1.15881 noise PoT
951763782 14.6012 good PoT
951763786 7.50032 good PoT
951763790 0.50676 good PoT
951763794 13.4125 noise PoT
951763798 3.45524 good PoT
951763802 14.2516 good PoT
951763806 2.36639 good LP
951763808 10.4327 good PoT
951763811 0.91494 noise PoT
951763815 8.95715 noise PoT
951763819 0.69669 good PoT
951763823 15.7534 good LP
951763828 20.426 good LP
951763833 5.54128 good LP
951763837 10.3832 good LP
951763841 18.6182 good LP
951763845 12.7977 good LP
951763849 11.4132 good LP
951763854 2.52108 noise LP
951763859 17.1477 good LP
951763863 0.59377 good LP
951763867 0.03658 good LP
951763874 0.01312 noise LP
951763880 0.02273 noise CA1
951763887 5.85025 good LP
951763893 5.0215 good LP
951763901 6.27197 good LP
951763907 9.34383 good LP
951763914 15.789 good LP
951763920 4.00488 good LP
951763928 5.38287 good LP
951763934 3.04221 good LP
951763941 0.00816 noise LP
951763947 1.57897 noise LP
951763954 11.8275 good LP
951763961 8.62689 good LP
951763968 8.3856 good LP
951763975 14.9898 good LP
951763982 12.1488 good LP
951763988 7.26286 good LP
951763994 5.46647 noise LP
951764001 11.7287 good LP
951764008 0.15738 good LP
951764014 2.82003 noise LGd
951764022 11.1967 good LP
951764029 5.63883 good LP
951764035 11.5555 good LP
951764042 12.2763 good LP
951764049 3.296 good LP
951764055 7.28983 good LP
951764063 7.33901 good LP
951764070 10.6127 good LP
951764076 3.39117 good LP
951764083 10.1095 good LP
951764090 14.326 good LP
951764099 11.0116 good LP
951764106 12.9879 good LP
951764112 8.86983 good LP
951764118 4.8696 good LGd
951764125 4.77381 good LGd
951764132 11.0504 good LGd
951764139 6.14549 good LGd
951764147 7.73138 good LGd
951764155 7.7847 good LGd
951764162 3.00635 good LGd
951764169 0.58705 good LGd
951764175 11.2825 good LGd
951764182 3.69808 good LGd
951764190 8.31926 good LGd
951764196 2.44906 good LGd
951764203 14.0843 good LGd
951764210 5.32293 good LGd
951764216 19.1162 good LGd
951764224 3.83655 good LGd
951764232 5.33502 good LGd
951764239 3.92841 good LGd
951764246 5.55037 good LGd
951764250 6.62693 good LGd
951764254 0.49198 noise LGd
951764259 7.92751 good LGd
951764263 5.8641 good LGd
951764268 4.06389 good LGd
951764272 14.842 good LGd
951764276 1.14734 noise LGd
951764279 10.7474 good LGd
951764284 4.16102 good LGd
951764287 4.80088 good LGd
951764293 16.162 good LGd
951764299 9.321 good LGd
951764305 12.0763 good LGd
951764312 13.7481 good LGd
951764319 2.25282 good LGd
951764325 14.3434 good LGd
951764332 6.43751 good LGd
951764338 6.4588 good LGd
951764344 12.0088 good LGd
951764350 10.6634 good LGd
951764357 11.6866 good LGd
951764364 6.12068 good LGd
951764370 14.4044 good LGd
951764374 4.53159 good LGd
951764379 4.49532 good LGd
951764385 8.29497 good LGd
951764390 3.70893 good LGd
951764396 5.75643 good LGd
951764403 1.74472 noise LGd
951764409 2.02507 noise LGd
951764415 22.8442 good LGd
951764421 11.9241 good LGd
951764426 2.71742 noise LGd
951764432 14.0462 good LGd
951764438 22.7161 good LGd
951764443 14.2488 good LGd
951764447 3.7575 good LGd
951764454 8.93462 good LGd
951764460 20.9761 good LGd
951764466 3.91136 good LGd
951764472 15.2495 good LGd
951764478 17.1805 good LGd
951764484 5.14984 good LGd
951764490 3.234 good LGd
951764496 10.2851 good LGd
951764503 20.7697 good LGd
951764508 3.69643 good LGd
951764514 12.4374 good LGd
951764520 10.2671 good LGd
951764525 5.52423 good LGd
951764531 12.6207 noise LGd
951764537 11.6708 noise LGd
951764543 3.67886 good LGd
951764550 4.92685 good LGd
951764557 9.14284 good LGd
951764563 10.5269 good LGd
951764570 11.5479 good LGd
951764576 6.09557 noise LGd
951764582 3.42961 noise LGd
951764589 5.32965 noise LGd
951764595 6.93115 noise LGd
951764601 3.70697 noise LGd
951764608 18.6999 good LGd
951764614 15.2261 good LGd
951764618 1.6015 good LGd
951764622 13.3591 good LGd
951764624 13.0301 good LGd
951764626 11.5823 good LGd
951764630 7.20716 good LGd
951764635 5.02522 good LGd
951764639 10.251 good LGd
951764644 13.5192 good LGd
951764648 8.21975 good LGd
951764652 6.23229 good LGd
951764656 5.28139 noise LGd
951764663 0.00093 noise LGd
951764669 3.9993 good LGd
951764675 4.10233 good LGd
951764681 1.56647 good LGd
951764688 1.50726 good LGd
951764694 2.66358 good LGd
951764700 4.42691 good LGd
951764706 10.0951 good LGd
951764714 3.74241 good LGd
951764718 9.8384 noise LGd
951764724 10.5901 good LGd
951764731 12.0302 good LGd
951764739 1.05082 noise LGd
951764746 0.00227 noise LGd
951764753 9.52085 good LGd
951764761 8.88574 noise LGd
951764768 9.13933 good LGd
951764776 3.37133 good LGd
951764783 23.1542 good LGd
951764791 5.49003 good LGd
951764798 10.1731 good LGd
951764809 20.4946 noise LGd
951764815 0.83423 noise LGd
951764821 0.83144 noise LGd
951764827 0.0031 noise LGd
951764835 9.1322 noise CA3
951764842 2.50341 good DG
951764848 0.71105 good DG
951764855 4.23894 good DG
951764862 2.10123 good DG
951764868 13.3805 good DG
951764875 1.47967 good DG
951764883 3.91798 noise DG
951764889 7.6392 noise DG
951764895 5.06408 good DG
951764903 6.99842 good DG
951764909 3.95053 noise DG
951764916 0.01033 noise DG
951764923 0.00558 noise DG
951764928 0.00765 noise DG
951764935 0.01354 noise DG
951764939 0.00827 noise DG
951764944 4.10667 noise DG
951764951 2.11601 good DG
951764958 2.80133 noise DG
951764964 4.36522 noise DG
951764971 1.73925 noise DG
951764977 3.93389 noise DG
951764983 3.26614 noise DG
951764990 1.58476 noise DG
951764995 1.82656 noise DG
951765001 0.65494 noise DG
951765009 18.7407 good DG
951765017 1.72437 noise CA1
951765023 2.14391 good CA1
951765031 6.40951 noise CA1
951765039 6.89932 noise CA1
951765044 6.80167 noise CA1
951765049 0.0031 noise CA1
951765055 0.04092 noise CA1
951765061 0.04764 good CA1
951765067 1.06364 good CA1
951765074 0.86037 noise CA1
951765080 3.61148 noise CA1
951765085 0.00713 noise CA1
951765093 0.0125 noise CA1
951765098 0.62353 good CA1
951765105 17.799 noise CA1
951765110 3.41453 noise CA1
951765118 1.60491 noise CA1
951765124 10.2191 noise CA1
951765132 6.29749 noise CA1
951765138 4.64836 noise CA1
951765145 5.76635 good CA1
951765151 12.9111 good CA1
951765159 25.3179 noise CA1
951765164 8.99611 noise CA1
951765170 5.02088 noise CA1
951765176 2.50662 good CA1
951765182 10.2026 good CA1
951765189 3.2618 noise CA1
951765195 0.83537 noise CA1
951765200 0.81367 noise CA1
951765206 0.65071 noise CA1
951765213 0.47751 good CA1
951765219 0.00651 noise CA1
951765225 5.07885 good CA1
951765231 2.53317 noise CA1
951765238 2.03313 noise CA1
951765243 5.11461 good CA1
951765247 7.2672 noise CA1
951765252 4.16857 good CA1
951765258 9.5782 good CA1
951765264 2.62855 good CA1
951765270 2.10805 good CA1
951765276 6.53124 good CA1
951765282 2.79348 good CA1
951765288 9.12827 good CA1
951765293 5.05044 good CA1
951765299 4.3677 good CA1
951765303 6.53413 good CA1
951765309 2.50352 good CA1
951765314 9.83788 good CA1
951765319 0.90471 good CA1
951765323 3.66574 good CA1
951765329 4.50648 good CA1
951765334 6.26566 good CA1
951765339 1.33551 good CA1
951765343 4.19781 good CA1
951765349 10.8901 good CA1
951765353 3.54545 good CA1
951765358 2.30501 good CA1
951765364 39.3285 good CA1
951765369 13.1377 good CA1
951765374 0.32385 noise CA1
951765379 2.20085 noise CA1
951765385 0.00785 good CA1
951765393 5.09063 noise CA1
951765396 0.00289 noise CA1
951765400 16.8106 noise CA1
951765405 33.1885 good CA1
951765411 11.0497 noise CA1
951765414 5.89448 good CA1
951765420 13.1448 good CA1
951765423 14.1916 good CA1
951765430 5.69876 good CA1
951765435 19.8853 good CA1
951765440 9.97935 good VISp
951765447 1.86221 good VISp
951765454 5.47349 good VISp
951765460 4.44892 good VISp
951765467 9.98162 good VISp
951765473 4.10409 noise VISp
951765478 17.4047 good VISp
951765485 13.9773 good VISp
951765490 5.27323 noise VISp
951765497 8.33011 noise VISp
951765502 13.287 noise VISp
951765508 2.13461 good VISp
951765513 3.90661 noise VISp
951765520 24.5397 noise VISp
951765525 12.0324 noise VISp
951765530 2.95127 good VISp
951765535 3.3674 good VISp
951765541 1.58972 good VISp
951765547 3.5935 good VISp
951765552 2.32971 good VISp
951765557 4.0796 good VISp
951765561 1.76766 good VISp
951765566 3.18388 good VISp
951765571 2.77426 good VISp
951765576 12.7688 noise VISp
951765582 14.778 good VISp
951765587 2.62793 good VISp
951765594 2.76868 good VISp
951765600 0.00796 noise VISp
951765606 7.46973 good VISp
951765611 23.9673 good VISp
951765617 2.60169 good VISp
951765623 6.50075 good VISp
951765629 3.00129 good VISp
951765635 0.11336 noise VISp
951765641 4.34527 good VISp
951765647 9.12497 good VISp
951765653 9.42195 good VISp
951765661 15.6626 good VISp
951765666 9.72245 good VISp
951765669 5.41325 good VISp
951765675 18.6652 good VISp
951765681 14.6917 good VISp
951765686 11.2814 good VISp
951765692 1.13855 good VISp
951765697 9.08022 good VISp
951765703 3.58978 noise VISp
951765710 0.003 noise VISp
951765716 3.34756 good VISp
951765721 10.0994 good VISp
951765727 15.782 good VISp
951765732 1.64645 good VISp
951765737 6.97155 good VISp
951765743 10.5288 noise VISp
951765747 13.0858 noise VISp
951765753 13.4251 noise VISp
951765758 13.2055 noise VISp
951765764 19.5368 noise VISp
951765769 7.64943 good VISp
951765775 0.31001 noise VISp
951765780 0.00289 noise VISp
951765786 2.58722 good VISp
951765793 7.54827 good VISp
951765801 1.88846 good VISp
951765809 5.72387 good VISp
951765815 0.00713 noise VISp
951765820 5.49643 good VISp
951765825 1.98983 good VISp
951765832 5.27602 noise VISp
951765836 1.17183 noise VISp
951765841 0.00858 noise VISp
951765849 1.28302 noise VISp
951765855 1.28787 good VISp
951765859 0.18828 noise VISp
951765866 3.43602 good VISp
951765870 0.45974 noise VISp
951765876 0.00134 noise VISp
951765881 1.33448 good VISp
951765886 3.61417 good VISp
951765892 0.73668 good VISp
951765898 21.7077 noise
951765904 0.91411 noise
951765910 10.1545 noise
951765913 10.8102 good LP
951765921 0.11367 good LP
951765926 9.27046 good LGd
951765931 5.00807 good LGd
951765944 1.90417 good LGd
951765950 1.62072 good LGd
951765955 0.16513 good DG
951765961 0.948 good DG
951765966 0.10117 good CA1
951765973 0.67416 good CA1
951765977 0.50407 good CA1
951765984 0.12969 noise CA1
951765988 0.45085 good CA1
951765995 1.32508 good VISp
951766001 0.1395 noise
951766007 0.57589 good DG
951766012 0.09083 good CA1
951766019 0.02501 good CA1
951766024 0.00837 good CA1
951766138 3.56684 good PO
951766144 10.9933 good PO
951766152 7.44338 good PO
951766160 4.75634 good PO
951766167 10.7141 good PO
951766173 9.36047 good PO
951766180 10.412 good PO
951766188 5.87175 good PO
951766195 8.16663 good PO
951766203 1.90221 good PO
951766208 12.5293 good PO
951766214 0.0589 noise PO
951766220 0.17577 good PO
951766225 5.32087 good PO
951766229 4.65135 good PO
951766235 0.96609 good PO
951766240 5.05385 good PO
951766245 3.38342 good PO
951766251 6.44888 good PO
951766256 0.70733 good PO
951766262 6.33583 good PO
951766266 8.58318 good PO
951766271 6.02665 good PO
951766276 2.62132 good PO
951766280 4.53841 good PO
951766286 6.32157 good PO
951766291 2.9985 good PO
951766298 8.71307 good PO
951766303 9.10947 good PO
951766309 27.6031 good LP
951766314 13.9623 good LP
951766322 13.2362 good LP
951766327 20.8808 good LP
951766334 9.46226 good PO
951766340 3.49089 good LP
951766346 7.1218 good LP
951766353 0.01281 good LP
951766360 0.39991 good LP
951766366 10.6936 good LP
951766372 12.1386 good LP
951766379 6.03647 good LP
951766385 3.86827 good LP
951766390 6.73223 good LP
951766398 1.86687 good LP
951766403 7.8248 good LP
951766408 10.6266 good LP
951766416 10.091 good LP
951766421 0.68915 good LP
951766427 7.16882 good LP
951766432 7.59136 good LP
951766438 5.55885 good LP
951766442 9.71284 good LP
951766447 13.6457 good LP
951766452 5.53095 good LP
951766458 15.2865 good LP
951766463 8.09647 good LP
951766469 0.06086 good LP
951766474 15.4068 good LP
951766480 6.592 good LP
951766485 1.00887 good LP
951766489 5.3901 good LP
951766494 5.21226 good LP
951766500 0.344 good LP
951766504 7.791 good LP
951766510 3.71916 good LP
951766515 14.5508 good LP
951766521 10.2152 good LP
951766526 7.57307 good LP
951766531 8.37578 good LP
951766541 15.5747 good LP
951766546 12.2331 good LP
951766552 6.38915 good LP
951766557 4.74549 good LP
951766562 0.16058 good LP
951766567 1.90572 good LP
951766573 14.5612 good LP
951766577 2.15807 good LP
951766582 6.21069 good LP
951766589 13.1292 good LP
951766593 2.40938 good LP
951766599 10.8013 good LP
951766605 0.91628 noise LP
951766611 8.05554 good LP
951766616 4.09551 good LP
951766621 4.53768 good LP
951766625 7.22948 good LP
951766630 17.7724 good LP
951766634 5.82938 good LP
951766636 10.1654 good LP
951766640 14.9032 good LP
951766645 9.48799 good LP
951766650 9.78735 good LP
951766657 4.37906 good LP
951766662 8.9896 good LP
951766673 19.209 good LP
951766679 4.43683 good LP
951766685 5.74878 good LP
951766691 0.12307 good LP
951766697 9.43415 good LP
951766704 14.0932 good LP
951766709 3.67142 good LP
951766714 5.80851 good LP
951766722 4.83012 good LP
951766727 7.53411 noise LP
951766732 9.49439 good LP
951766738 0.03865 good LP
951766743 6.11428 good LP
951766749 10.5625 good LP
951766754 4.75293 good LP
951766761 2.22317 noise LP
951766767 6.77501 good LP
951766773 5.93778 good LP
951766780 9.65053 noise LP
951766785 0.00289 noise LP
951766791 12.2685 good LP
951766797 9.73103 good LP
951766803 1.74886 good LP
951766809 5.3809 good LP
951766816 13.8656 good LP
951766820 4.09675 noise LP
951766828 3.99424 good LP
951766833 3.1071 good LP
951766840 0.74164 good LP
951766846 3.07569 good LP
951766853 0.11636 good LP
951766860 0.19882 good LP
951766867 5.40002 good LP
951766873 6.75093 good LP
951766879 10.7436 good LP
951766886 1.85229 good LP
951766893 6.92133 good LP
951766899 6.3007 good LP
951766906 4.72048 good LP
951766912 6.60729 good LP
951766918 0.34101 good LP
951766923 1.02189 good LP
951766928 1.23497 good LP
951766933 0.08133 good LP
951766938 6.78389 good LP
951766942 7.80795 good LP
951766948 6.11903 good LP
951766952 13.0386 good LP
951766957 1.97123 good LP
951766960 1.76363 good LP
951766965 6.69885 good LP
951766968 1.38088 good LP
951766973 0.0062 good LP
951766978 4.07247 noise LP
951766983 0.16131 good LP
951766990 12.6832 good LP
951766995 1.32249 good LP
951767001 2.79089 good LP
951767006 3.95456 good LP
951767013 1.88857 good LP
951767020 1.77717 noise LP
951767025 2.16158 noise LP
951767033 0.14818 noise LP
951767038 1.78885 good LP
951767045 5.89758 good LP
951767050 11.6229 good LP
951767056 5.01468 good LP
951767061 4.74084 good LP
951767067 5.18054 good LP
951767074 8.54753 good LP
951767078 2.8839 good LP
951767086 17.4824 noise LP
951767092 2.35626 good LP
951767098 6.15344 good LP
951767104 1.92845 noise LP
951767108 5.38793 good LP
951767112 9.06679 good LP
951767120 4.13839 good LP
951767125 3.19928 noise LP
951767133 3.54359 good LP
951767138 3.67855 good LP
951767144 4.2285 good LP
951767152 8.61593 good LP
951767157 1.58776 noise LP
951767164 9.383 noise DG
951767169 3.17086 noise DG
951767177 2.97917 noise DG
951767182 7.54455 noise DG
951767190 0.09238 good DG
951767195 2.75473 good DG
951767202 3.80731 noise DG
951767209 5.08578 good DG
951767217 0.1054 good DG
951767223 6.24179 good DG
951767230 0.08897 good DG
951767242 10.0404 good DG
951767247 1.57566 good DG
951767253 8.11517 good CA1
951767258 4.49191 noise DG
951767263 3.47787 noise DG
951767269 1.71785 noise DG
951767274 0.48785 noise CA1
951767280 13.4059 good DG
951767285 1.1801 good DG
951767291 7.60314 noise CA1
951767297 5.39754 noise CA1
951767304 1.49341 good CA1
951767310 20.5422 good CA1
951767318 0.76107 good CA1
951767322 0.1455 good CA1
951767329 3.09563 noise CA1
951767334 5.63676 noise CA1
951767340 4.63348 noise CA1
951767346 6.02128 noise CA1
951767351 1.51118 noise CA1
951767358 0.50418 noise CA1
951767364 0.4586 noise CA1
951767370 5.1362 noise CA1
951767376 3.00521 noise CA1
951767383 2.80598 noise CA1
951767389 0.93684 noise CA1
951767395 1.53702 noise CA1
951767402 1.03677 noise CA1
951767408 0.03968 noise CA1
951767415 0.16286 noise CA1
951767422 3.12963 noise CA1
951767428 0.00806 noise CA1
951767433 0.48826 noise CA1
951767438 4.72493 good CA1
951767443 0.44 noise CA1
951767450 0.01478 noise CA1
951767455 2.51437 good CA1
951767461 1.6666 good CA1
951767468 6.65524 noise CA1
951767474 4.99029 noise CA1
951767481 2.13409 good CA1
951767487 15.1874 good CA1
951767493 0.00765 noise CA1
951767500 2.84287 good CA1
951767507 1.90045 noise CA1
951767514 1.88309 good CA1
951767520 2.06217 good CA1
951767526 2.5247 noise CA1
951767532 6.72251 good CA1
951767538 0.62498 good CA1
951767544 0.76841 good CA1
951767547 0.21701 noise CA1
951767552 0.27684 noise CA1
951767556 2.96853 noise CA1
951767562 0.29637 noise CA1
951767566 0.71446 good CA1
951767573 7.00834 good CA1
951767580 0.01715 good CA1
951767586 5.66043 good CA1
951767594 3.2216 good CA1
951767599 1.25687 noise CA1
951767606 1.26183 good CA1
951767612 6.88134 good CA1
951767618 4.13209 good CA1
951767624 3.92211 good CA1
951767631 0.00496 good CA1
951767636 0.19076 noise CA1
951767643 4.95309 good CA1
951767649 6.09692 good CA1
951767655 1.171 good CA1
951767661 7.66545 good CA1
951767667 1.09298 good CA1
951767674 0.24584 good CA1
951767681 0.22228 good CA1
951767688 1.44722 noise CA1
951767694 0.24387 noise CA1
951767700 0.04929 good CA1
951767707 0.01829 noise CA1
951767713 17.364 good CA1
951767719 1.35949 good CA1
951767725 14.6946 good CA1
951767730 13.7188 good CA1
951767738 2.12593 good CA1
951767743 1.28085 noise CA1
951767750 1.1275 good CA1
951767757 0.86709 good CA1
951767763 0.25875 good CA1
951767770 2.86085 good CA1
951767776 2.16685 noise CA1
951767782 1.31753 good CA1
951767789 4.99897 good CA1
951767795 2.74997 good CA1
951767803 4.23677 good CA1
951767810 2.37765 good CA1
951767821 4.38216 good CA1
951767827 4.35674 good CA1
951767832 3.53626 good CA1
951767838 2.72631 good CA1
951767845 0.74929 noise CA1
951767852 0.26867 noise CA1
951767857 1.92391 good CA1
951767862 0.6289 noise CA1
951767868 2.15331 noise CA1
951767873 2.78717 good CA1
951767879 1.65482 good CA1
951767884 0.02883 good CA1
951767892 0.20926 good CA1
951767897 26.7566 good CA1
951767903 4.96601 good CA1
951767907 1.15405 good CA1
951767915 2.33498 good CA1
951767920 11.689 good CA1
951767927 4.05283 good CA1
951767933 1.48814 good CA1
951767939 3.34074 good CA1
951767945 4.65301 good CA1
951767950 11.2101 good CA1
951767956 3.27482 good CA1
951767960 7.71826 good CA1
951767966 7.05711 good CA1
951767973 1.25284 good CA1
951767979 2.99633 good CA1
951767984 0.48289 good CA1
951767991 5.21691 good CA1
951767997 2.56841 good CA1
951768004 4.48581 good CA1
951768010 4.42339 good CA1
951768018 8.212 good CA1
951768023 4.26932 good CA1
951768030 2.22027 good CA1
951768035 3.24588 noise CA1
951768042 3.34725 noise CA1
951768047 2.89165 good CA1
951768054 18.1724 good CA1
951768060 0.46429 noise CA1
951768067 3.65075 good CA1
951768073 2.28259 noise CA1
951768080 1.55624 good CA1
951768086 0.1579 good CA1
951768093 3.65344 good CA1
951768098 4.65538 noise CA1
951768105 13.1174 good CA1
951768109 2.4225 noise CA1
951768115 0.42089 noise CA1
951768121 0.28893 noise VISp
951768127 3.07114 noise VISp
951768133 12.0295 good VISp
951768139 4.95733 good VISp
951768144 3.58524 noise VISp
951768149 3.98442 noise VISp
951768154 5.94749 good VISp
951768160 2.84969 good VISp
951768165 5.99213 noise VISp
951768170 4.00664 good VISp
951768177 2.6113 good VISp
951768183 5.32107 good VISp
951768188 3.62843 good VISp
951768196 1.16005 good VISp
951768201 4.48178 noise VISp
951768209 1.65337 good VISp
951768215 2.43232 good VISp
951768222 38.6918 good VISp
951768228 1.4528 good VISp
951768234 0.04402 good VISp
951768239 2.24094 good VISp
951768247 6.3691 good VISp
951768252 0.95854 good VISp
951768258 2.92234 good VISp
951768266 1.54962 good VISp
951768272 0.11047 good VISp
951768278 9.61519 good VISp
951768285 3.60332 good VISp
951768291 2.06661 good VISp
951768298 7.5058 good VISp
951768307 3.44108 good VISp
951768313 2.51974 noise VISp
951768318 11.362 good VISp
951768327 1.25057 good VISp
951768332 18.085 good VISp
951768340 2.44038 good VISp
951768345 4.23646 good VISp
951768352 1.72974 good VISp
951768356 3.20248 noise VISp
951768363 1.26452 good VISp
951768369 4.01356 good VISp
951768374 10.5394 good VISp
951768382 11.6807 good VISp
951768390 27.369 good VISp
951768402 7.5028 good VISp
951768408 11.9073 good VISp
951768415 1.64232 good VISp
951768421 11.2489 good VISp
951768427 5.18322 good VISp
951768434 10.6732 good VISp
951768441 23.9354 good VISp
951768446 14.5898 good VISp
951768451 11.3477 good VISp
951768457 9.15917 good VISp
951768462 3.18564 good VISp
951768467 1.92143 good VISp
951768473 8.20703 good VISp
951768480 5.17423 good VISp
951768487 0.31145 good VISp
951768495 16.5755 good VISp
951768500 11.2425 good VISp
951768506 0.13651 good VISp
951768511 6.84621 good VISp
951768519 0.21856 good VISp
951768524 4.24338 good VISp
951768530 2.67815 good VISp
951768538 4.26591 good VISp
951768544 2.18772 good VISp
951768550 2.01825 good VISp
951768557 7.48875 good VISp
951768563 1.62082 good VISp
951768568 7.46457 good VISp
951768575 1.83111 good VISp
951768581 4.42153 good VISp
951768586 2.11725 good VISp
951768593 2.39016 good VISp
951768598 1.75857 good VISp
951768604 6.47378 good VISp
951768611 0.82968 good VISp
951768616 1.5769 good VISp
951768621 3.24547 good VISp
951768627 11.0219 good VISp
951768632 4.57457 good VISp
951768637 2.74026 noise VISp
951768643 1.4684 good VISp
951768649 5.50615 good VISp
951768655 2.28073 good VISp
951768660 0.7403 good VISp
951768668 2.53855 good VISp
951768673 1.92969 good VISp
951768681 0.49353 good VISp
951768686 3.26159 noise VISp
951768693 2.85889 good VISp
951768699 4.46896 good VISp
951768705 4.19585 good VISp
951768712 4.65549 good VISp
951768717 1.42169 good VISp
951768723 5.12256 good VISp
951768729 1.35205 noise VISp
951768735 0.81573 good VISp
951768739 1.94953 good VISp
951768745 2.27897 noise VISp
951768749 2.02352 good VISp
951768754 1.3661 good VISp
951768760 4.04994 noise VISp
951768766 8.87438 good VISp
951768771 8.05575 noise VISp
951768776 0.03441 good VISp
951768782 0.1641 good VISp
951768786 3.67638 noise VISp
951768793 4.23739 good VISp
951768797 0.88393 good VISp
951768802 0.00651 good VISp
951768807 2.17615 good VISp
951768810 2.27835 noise VISp
951768815 2.70812 good VISp
951768820 5.31446 noise VISp
951768823 6.52535 good VISp
951768830 10.9098 good VISp
951768835 7.83947 good VISp
951768842 2.49308 good VISp
951768848 4.81886 noise VISp
951768854 3.75047 noise VISp
951768861 0.24088 good VISp
951768867 0.03813 good VISp
951768875 0.94707 good VISp
951768881 2.06258 good VISp
951768888 2.90921 good VISp
951768894 9.16155 good VISp
951768901 3.99186 good VISp
951768907 2.85765 good VISp
951768913 0.0712 good VISp
951768920 1.85539 good VISp
951768925 2.28806 good VISp
951768932 0.78329 noise VISp
951768937 0.08412 good VISp
951768944 0.96981 good VISp
951768950 0.37893 noise VISp
951768957 10.2835 noise
951768969 6.83019 noise
951768974 1.00556 noise
951768980 6.48257 good PO
951768986 8.03663 good PO
951768990 1.87875 good PO
951768995 4.25578 good PO
951769002 0.03389 good LP
951769007 15.5288 good LP
951769012 1.77727 good LP
951769018 2.70678 good LP
951769024 7.12573 good LP
951769029 11.3657 good LP
951769034 10.5122 good LP
951769041 1.54229 good LP
951769046 6.2699 good LP
951769054 2.17036 good LP
951769060 2.35905 good LP
951769068 3.05016 good LP
951769074 0.03823 good LP
951769081 14.6808 good LP
951769088 2.94218 good LP
951769094 7.31804 good LP
951769100 2.82582 good LP
951769106 7.54703 good LP
951769112 2.67371 good LP
951769119 6.08782 good LP
951769125 2.68911 good LP
951769131 1.97671 good LP
951769138 2.61677 good LP
951769144 1.13215 good LP
951769149 3.25725 good LP
951769156 1.14785 good DG
951769162 0.04485 good DG
951769169 0.04433 good DG
951769174 1.73439 noise DG
951769182 0.13651 good DG
951769187 1.45662 noise CA1
951769194 1.14785 noise CA1
951769200 0.28438 noise CA1
951769207 0.01054 noise CA1
951769213 0.0156 noise CA1
951769220 0.00889 noise CA1
951769226 0.03348 noise CA1
951769233 0.04309 good CA1
951769238 0.01932 noise CA1
951769246 0.14777 good CA1
951769251 2.34118 good CA1
951769259 0.10148 good CA1
951769264 1.08802 good CA1
951769272 0.02769 good CA1
951769277 0.02108 good CA1
951769284 0.45054 good VISp
951769289 0.28851 good VISp
951769295 3.27275 good VISp
951769299 4.57933 good VISp
951769304 2.04729 good VISp
951769309 1.31185 good VISp
951769314 1.02519 good VISp
951769319 0.83041 good VISp
951769325 0.75714 good VISp
951769330 1.10104 good VISp
951769334 0.07223 good VISp
951769339 0.3778 good VISp
951769344 0.94873 good VISp
951769351 0.25638 good VISp
951769355 0.05136 good VISp
951769362 0.04464 good VISp
951769365 0.03141 good VISp
951769371 0.25679 good VISp
951769377 0.16978 noise
951769383 0.08019 good LP
951769390 0.21091 good DG
951769395 0.03947 good DG
951769401 0.16813 noise CA1
951769406 0.0434 noise CA1
951769412 0.05704 noise CA1
951769418 0.01963 noise CA1
951769424 0.15046 good VISp
951769429 0.03513 good VISp
951769435 0.07027 good VISp
951769443 0.09135 good DG
951769448 0.04681 good DG
951769456 0.04392 noise CA1
951769462 0.00827 noise CA1
951769470 0.07368 noise CA1
951769475 0.05043 noise CA1
951769482 3.38115 good CA1
951769487 0.26702 noise CA1
951769493 0.40022 good VISp
951769500 0.06045 good VISp
951769506 0.05539 noise CA1
951769514 0.02098 noise CA1
951769521 0.0371 noise CA1
951769527 0.01674 noise CA1
951769538 0.01116 noise CA1
951769546 0.14694 good VISp
951769554 0.07172 noise CA1
951769645 1.43048 good APN
951769654 2.99788 good APN
951769662 33.2358 good APN
951769668 19.8743 good APN
951769674 0.00413 noise APN
951769681 3.13717 good APN
951769688 3.78963 good APN
951769694 30.0669 good APN
951769698 37.0382 good APN
951769706 2.10733 good APN
951769711 1.39586 good APN
951769718 0.04795 good APN
951769724 1.20748 good APN
951769730 1.56461 good APN
951769737 0.54086 good APN
951769744 11.9715 good APN
951769751 1.9887 good APN
951769758 1.55376 good APN
951769764 3.96613 good APN
951769771 51.3402 good APN
951769776 1.74369 good APN
951769784 0.36385 good APN
951769790 32.9643 good APN
951769797 1.20262 good APN
951769803 25.6825 good APN
951769808 45.8666 good APN
951769813 0.51606 good APN
951769818 12.9885 good APN
951769822 0.05198 good APN
951769826 38.6449 good APN
951769833 33.3518 good APN
951769839 0.30897 good APN
951769846 2.36701 noise APN
951769857 6.66723 good APN
951769864 4.09944 noise APN
951769870 1.66247 good APN
951769875 3.81971 good APN
951769878 27.2155 good APN
951769883 2.62452 good APN
951769890 25.5366 good APN
951769898 25.2519 good APN
951769905 20.452 good APN
951769911 2.5649 noise APN
951769917 0.6165 good APN
951769923 47.8529 good APN
951769930 6.53403 good APN
951769935 3.4045 noise APN
951769941 33.4774 good APN
951769948 39.7706 good APN
951769953 0.00682 good APN
951769959 8.49503 good APN
951769966 0.20957 noise APN
951769971 1.13907 good APN
951769978 35.3371 good APN
951769985 10.3165 good APN
951769992 0.37335 good APN
951769999 2.20922 noise APN
951770005 5.12298 good APN
951770012 4.62014 noise APN
951770018 13.4504 good APN
951770024 9.66686 good APN
951770031 1.18785 good APN
951770036 41.438 good APN
951770042 3.69715 good APN
951770049 19.4763 noise APN
951770053 8.94733 good APN
951770058 0.70961 noise APN
951770063 13.2811 good APN
951770068 38.2703 good APN
951770072 2.30067 good APN
951770077 0.30856 good APN
951770082 2.02931 good APN
951770087 0.0124 noise APN
951770091 1.88815 good APN
951770093 46.1365 good APN
951770098 0.03224 good APN
951770102 0.0094 noise APN
951770105 0.01529 good APN
951770111 0.24811 good APN
951770116 0.01416 noise APN
951770121 0.01157 noise APN
951770127 0.02253 good APN
951770132 2.404 good APN
951770136 0.5267 good APN
951770142 2.90952 good APN
951770147 2.11745 good APN
951770154 10.0171 good APN
951770159 0.18766 good APN
951770164 5.28366 noise APN
951770170 17.817 good APN
951770178 3.51083 noise APN
951770183 6.9079 good APN
951770188 35.2797 good APN
951770196 8.93566 good APN
951770200 4.70416 good APN
951770205 6.16409 good APN
951770210 0.75301 good APN
951770214 5.3033 good APN
951770220 28.654 good APN
951770224 8.07962 good APN
951770229 2.06527 good APN
951770234 22.1688 good APN
951770238 5.75922 good APN
951770243 2.45495 good APN
951770248 0.73585 good APN
951770251 2.08718 noise APN
951770258 0.09435 noise APN
951770264 0.13196 good APN
951770270 0.02542 good APN
951770276 3.03642 good APN
951770283 13.0684 good APN
951770288 36.0112 good APN
951770295 7.37415 good APN
951770300 18.2104 good APN
951770307 0.15242 good APN
951770312 3.81661 good APN
951770315 12.5504 good APN
951770321 4.15937 good APN
951770327 2.71463 good APN
951770333 41.5639 good APN
951770340 3.59846 good APN
951770347 2.79255 good APN
951770353 0.00114 good APN
951770358 15.6871 good APN
951770366 4.55928 good APN
951770375 0.00434 good APN
951770379 0.68574 good APN
951770386 0.76241 good APN
951770391 0.38668 noise APN
951770397 0.05208 good APN
951770401 0.40373 noise APN
951770406 3.30272 good APN
951770412 4.56641 good APN
951770417 2.03014 good APN
951770423 40.8491 good APN
951770428 7.49309 good APN
951770434 42.6069 good APN
951770439 44.0604 good APN
951770446 9.16289 good APN
951770452 3.19711 good APN
951770457 6.71766 good APN
951770465 8.21706 good APN
951770470 8.14875 good APN
951770477 37.1047 good APN
951770484 5.17609 good APN
951770489 0.94955 good APN
951770497 0.73007 good APN
951770501 4.21404 good POL
951770508 1.8741 good POL
951770513 4.27707 good POL
951770519 0.70237 good POL
951770525 1.99056 good POL
951770530 0.0062 good POL
951770536 0.05177 good POL
951770542 0.19747 good POL
951770548 1.45735 good POL
951770556 0.10809 noise POL
951770561 1.84444 good POL
951770569 0.14798 noise POL
951770574 16.8392 noise LP
951770580 0.00765 noise LP
951770586 7.93485 good LP
951770592 1.68127 good LP
951770599 0.13227 good LP
951770604 5.58602 good LP
951770610 0.3222 good LP
951770618 0.14901 good LP
951770623 0.16317 noise LP
951770630 0.05311 noise LP
951770636 1.18382 noise LP
951770641 1.42738 noise DG
951770647 2.63909 noise DG
951770653 0.93426 noise DG
951770658 3.0141 noise DG
951770663 21.2313 noise DG
951770670 1.88836 noise DG
951770674 2.97886 noise DG
951770680 0.01767 good DG
951770685 0.08742 noise DG
951770691 0.94656 good DG
951770696 0.0744 good DG
951770704 0.95203 noise DG
951770708 1.23135 good DG
951770714 1.40785 good DG
951770720 12.3374 good DG
951770728 13.9405 good DG
951770735 1.29015 noise DG
951770742 3.76835 good DG
951770748 1.0222 good DG
951770755 7.26544 good DG
951770760 0.29544 noise DG
951770768 0.5141 noise DG
951770773 11.2351 noise DG
951770780 3.64 good DG
951770785 3.57532 noise DG
951770791 0.00537 noise DG
951770795 1.7439 noise DG
951770802 0.4058 noise CA1
951770808 0.29275 noise CA1
951770814 2.82355 noise DG
951770822 5.15015 noise CA1
951770828 2.51685 noise CA1
951770834 9.90298 noise CA1
951770842 3.29125 noise CA1
951770847 0.00434 good CA1
951770854 1.60326 noise CA1
951770860 2.06372 good CA1
951770867 2.47717 noise CA1
951770873 3.86228 good CA1
951770880 0.34214 noise CA1
951770886 1.24447 noise CA1
951770891 3.36224 noise CA1
951770896 4.17508 noise CA1
951770901 2.79089 noise CA1
951770908 0.65711 good CA1
951770914 2.69304 noise CA1
951770921 2.56759 noise CA1
951770928 3.41143 good CA1
951770943 0.82007 noise CA1
951770949 7.27515 good CA1
951770955 3.869 good CA1
951770960 3.89628 good CA1
951770965 2.26109 good CA1
951770969 0.96547 noise CA1
951770976 5.17216 good CA1
951770981 3.4756 good CA1
951770987 3.96231 good CA1
951770994 7.32072 good CA1
951771000 1.40661 noise CA1
951771005 4.06492 good CA1
951771013 5.3747 good CA1
951771018 1.93496 good CA1
951771024 8.65086 good CA1
951771032 6.05693 good CA1
951771038 1.6262 noise CA1
951771043 1.92535 good CA1
951771050 10.1953 good CA1
951771057 5.83796 good CA1
951771064 14.5114 good CA1
951771069 2.92957 good CA1
951771077 0.01912 good CA1
951771083 3.73104 good CA1
951771089 1.26979 good CA1
951771095 3.76111 noise CA1
951771103 4.8884 good CA1
951771110 5.96702 good CA1
951771115 0.84911 good CA1
951771121 3.54969 good CA1
951771128 6.16161 good CA1
951771135 3.06256 good CA1
951771142 4.31344 good CA1
951771148 2.52987 good CA1
951771155 0.56235 good CA1
951771161 8.70253 good CA1
951771167 7.51086 good CA1
951771174 9.14336 good CA1
951771180 7.4625 good CA1
951771188 3.9774 good CA1
951771194 0.02645 noise CA1
951771199 7.97298 good CA1
951771206 2.36866 good CA1
951771211 5.55864 good CA1
951771218 0.38296 good CA1
951771224 7.28487 good CA1
951771229 2.20705 good CA1
951771234 1.37302 good CA1
951771239 2.48233 good CA1
951771246 1.51552 good CA1
951771252 0.91514 noise CA1
951771257 0.14436 noise CA1
951771263 5.93799 good CA1
951771270 0.87722 noise CA1
951771276 0.47348 noise CA1
951771283 3.91767 good CA1
951771288 23.3667 good CA1
951771294 1.09433 good CA1
951771300 1.47967 noise CA1
951771307 1.63054 noise CA1
951771313 24.9118 good VISam
951771320 6.55645 good VISam
951771326 3.15164 good VISam
951771331 7.01433 good VISam
951771338 2.82262 good VISam
951771344 1.48122 noise VISam
951771349 0.00496 good VISam
951771357 0.39929 good VISam
951771362 2.05752 noise VISam
951771368 5.53353 good VISam
951771374 7.31979 good VISam
951771381 2.6857 noise VISam
951771387 16.6017 good VISam
951771393 1.57887 good VISam
951771400 1.9175 good VISam
951771405 5.89996 good VISam
951771412 1.98229 good VISam
951771418 3.86786 good VISam
951771425 0.40549 good VISam
951771431 5.86503 good VISam
951771438 4.19388 good VISam
951771443 1.38098 good VISam
951771449 1.79143 good VISam
951771453 3.01431 good VISam
951771458 1.86583 good VISam
951771465 0.02914 noise VISam
951771471 0.03493 noise VISam
951771477 0.35723 good VISam
951771483 0.86812 good VISam
951771488 2.25034 good VISam
951771494 1.36796 good VISam
951771499 1.9794 good VISam
951771507 2.54867 good VISam
951771512 4.34724 good VISam
951771517 3.91891 noise VISam
951771522 4.67925 good VISam
951771528 0.57196 good VISam
951771533 0.68016 good VISam
951771538 2.74791 good VISam
951771543 2.02022 good VISam
951771547 4.78693 good VISam
951771552 2.32061 noise VISam
951771558 6.86873 good VISam
951771563 0.11915 good VISam
951771568 0.00651 good VISam
951771572 2.39574 good VISam
951771577 3.0018 good VISam
951771583 5.8083 good VISam
951771588 5.41314 good VISam
951771594 3.27368 good VISam
951771601 5.52867 good VISam
951771607 1.00194 good VISam
951771613 4.61436 good VISam
951771620 6.89674 good VISam
951771626 1.36703 good VISam
951771633 2.41093 good VISam
951771639 11.5399 good VISam
951771645 4.6558 good VISam
951771652 5.98996 good VISam
951771658 11.5414 good VISam
951771665 8.46951 good VISam
951771670 13.1894 good VISam
951771676 9.0145 good VISam
951771684 18.1031 good VISam
951771690 10.0666 good VISam
951771697 5.62436 good VISam
951771701 7.59312 good VISam
951771706 2.95881 good VISam
951771712 19.8755 good VISam
951771718 2.07374 good VISam
951771724 8.25695 good VISam
951771730 4.56145 good VISam
951771735 14.1265 good VISam
951771742 4.94235 good VISam
951771747 6.43018 good VISam
951771753 1.40289 good VISam
951771759 0.84095 good VISam
951771764 0.37914 good VISam
951771771 2.218 good VISam
951771777 3.94567 good VISam
951771782 9.33443 good VISam
951771788 3.70903 noise VISam
951771794 2.83161 good VISam
951771800 3.41215 good VISam
951771806 3.12219 good VISam
951771813 1.75506 good VISam
951771818 3.30881 good VISam
951771824 6.21451 good VISam
951771831 2.3697 good VISam
951771837 3.87396 noise VISam
951771844 2.08521 good VISam
951771850 3.78664 good VISam
951771856 1.62589 good VISam
951771862 2.99746 good VISam
951771866 0.01044 good VISam
951771872 1.64263 good VISam
951771878 4.61539 good VISam
951771885 4.81121 good VISam
951771892 0.48216 noise VISam
951771898 21.6197 good VISam
951771904 3.51838 noise VISam
951771910 12.4171 good VISam
951771918 8.58276 good VISam
951771924 1.99087 noise VISam
951771931 10.2836 good VISam
951771938 2.95086 good VISam
951771944 3.20909 noise
951771951 0.93333 noise
951771958 7.62329 noise
951771965 5.10593 noise
951771971 0.51761 good APN
951771979 0.03338 good APN
951771985 0.17319 noise APN
951771992 39.7843 good APN
951771998 0.24522 good APN
951772005 0.33904 good APN
951772012 0.12359 good APN
951772018 0.21732 good APN
951772026 33.3255 good APN
951772032 1.78823 good APN
951772037 0.07182 good APN
951772045 0.15562 good POL
951772049 0.10788 good POL
951772057 0.034 good POL
951772063 0.91008 good POL
951772073 0.28097 good POL
951772078 0.31662 good LP
951772083 0.86719 good DG
951772090 2.37993 good DG
951772095 0.09941 good CA1
951772101 0.46284 good VISam
951772107 0.80612 good VISam
951772113 0.5328 good VISam
951772119 0.14643 noise
951772125 0.06965 good APN
951772131 0.08639 good POL
951772137 0.05384 good POL
951772142 0.03472 good POL
951772147 0.61784 good APN
951772153 0.04557 good DG
951772159 0.24501 good CA1
951772221 4.70457 good VPM
951772227 3.72102 good VPM
951772233 4.29154 good VPM
951772239 2.28093 noise VPM
951772247 4.57168 noise VPM
951772253 3.104 noise VPM
951772260 3.12601 good VPM
951772266 0.01395 good VPM
951772273 9.67812 good VPM
951772280 3.65292 good VPM
951772286 5.45903 good VPM
951772293 0.12597 good VPM
951772298 6.74628 good VPM
951772304 10.3528 good VPM
951772310 1.77521 noise VPM
951772316 10.7254 good VPM
951772322 8.32804 good VPM
951772328 6.40651 good VPM
951772334 18.4867 good VPM
951772340 5.77689 noise VPM
951772344 0.73565 noise VPM
951772351 2.77353 good VPM
951772355 15.4752 good VPM
951772361 15.1415 good VPM
951772367 13.1557 good VPM
951772373 9.70323 good VPM
951772379 7.98435 good VPM
951772385 12.4186 good VPM
951772391 3.13418 good VPM
951772397 11.6179 good VPM
951772402 11.3955 good VPM
951772407 2.20756 noise VPM
951772413 10.3179 good VPM
951772419 1.6946 good VPM
951772428 10.7328 good VPM
951772434 12.0966 good VPM
951772441 5.97333 good VPM
951772448 0.38296 good VPM
951772455 18.6347 good VPM
951772462 8.74727 good VPM
951772468 1.84847 noise VPM
951772475 9.45988 good VPM
951772482 7.84856 good VPM
951772489 0.06582 good VPM
951772495 11.0722 good VPM
951772502 2.96905 good VPM
951772509 17.9442 good VPM
951772515 3.88615 noise VPM
951772523 4.55339 noise VPM
951772529 14.0161 good VPM
951772535 6.00805 good VPM
951772541 8.51777 good VPM
951772548 8.34685 good VPM
951772555 3.23121 good VPM
951772561 0.59077 good VPM
951772569 0.12566 noise VPM
951772576 11.8787 good VPM
951772581 4.21889 good VPM
951772589 7.18174 good VPM
951772595 3.95766 good VPM
951772600 8.49968 good VPM
951772606 1.89136 good VPM
951772612 15.3178 good VPM
951772618 8.75554 good VPM
951772623 4.32357 good VPM
951772630 2.79782 good VPM
951772635 7.88483 good VPM
951772640 19.2235 good VPM
951772647 11.4084 good VPM
951772653 8.2618 good VPM
951772659 15.0126 good VPM
951772665 4.13767 good VPM
951772671 7.32217 good VPM
951772678 2.33477 good VPM
951772685 4.5414 good VPM
951772690 14.0128 good VPM
951772696 10.392 good VPM
951772703 0.6567 good VPM
951772710 1.17059 noise VPM
951772716 0.26392 noise VPM
951772723 14.0084 good VPM
951772728 2.47551 noise VPM
951772734 6.73936 good VPM
951772739 9.04798 good VPM
951772745 13.1074 good VPM
951772751 13.2988 good VPM
951772757 11.6707 good VPM
951772761 13.112 good VPM
951772766 16.3706 good VPM
951772774 0.82658 good VPM
951772782 0.01033 good VPM
951772789 6.37034 good VPM
951772795 8.44626 good VPM
951772802 5.88198 good VPM
951772809 7.97732 noise VPM
951772815 2.64416 good VPM
951772822 7.36898 good VPM
951772829 0.13041 noise VPM
951772835 17.3807 good VPM
951772842 7.26906 good VPM
951772849 8.62214 good VPM
951772855 1.47367 noise VPM
951772864 4.52611 good VPM
951772870 1.61958 good VPM
951772876 8.47416 good VPM
951772884 12.4035 good VPM
951772890 0.17412 good VPM
951772896 1.20283 good VPM
951772900 0.94242 good VPM
951772906 22.9855 good VPM
951772914 1.54022 noise VPM
951772920 1.10528 noise VPM
951772926 9.69156 good VPM
951772932 12.5661 good VPM
951772938 8.21799 good VPM
951772945 8.04211 good VPM
951772952 7.12284 good VPM
951772958 8.39697 good VPM
951772963 5.69318 good VPM
951772969 15.0003 good VPM
951772975 18.025 good VPM
951772981 8.63671 noise VPM
951772987 9.09717 good VPM
951772993 1.1494 good VPM
951773000 14.0709 good VPM
951773011 4.41874 good VPM
951773018 3.55971 good VPM
951773024 0.77678 good VPM
951773030 5.0059 good VPM
951773035 11.9163 good VPM
951773043 15.1822 good VPM
951773049 6.09082 good VPM
951773054 1.77428 good VPM
951773061 6.19881 good VPM
951773069 11.9444 good VPM
951773075 11.032 good VPM
951773083 15.5343 good VPM
951773089 10.2341 good VPM
951773096 19.8385 good VPM
951773103 14.4526 good VPM
951773110 10.6374 good VPM
951773117 5.88622 good VPM
951773123 5.89552 good VPM
951773131 3.35097 good VPM
951773137 9.55154 good VPM
951773144 45.8654 good VPM
951773151 5.87702 good VPM
951773158 1.78802 good VPM
951773164 6.55614 good VPM
951773171 20.5879 good VPM
951773178 7.93516 good VPM
951773184 7.36464 good VPM
951773189 5.8487 good VPM
951773195 12.4258 good VPM
951773200 7.92534 good VPM
951773205 2.09927 good VPM
951773211 24.5946 good VPM
951773216 8.96087 good VPM
951773222 2.38499 good VPM
951773227 28.6015 good VPM
951773233 27.4672 good VPM
951773238 21.7692 good VPM
951773242 2.26584 good VPM
951773246 7.70462 good VPM
951773251 5.49767 good VPM
951773257 16.671 good VPM
951773262 13.6102 good VPM
951773268 5.20575 good VPM
951773273 7.88153 good VPM
951773278 3.29879 good VPM
951773284 5.82824 good VPM
951773289 21.2072 good VPM
951773295 0.88755 noise VPM
951773300 17.8141 good VPM
951773305 0.66001 good LGd
951773310 0.00909 noise LGd
951773315 4.69124 good LGd
951773320 11.3156 good LGd
951773325 4.03867 good LGd
951773332 3.75285 good LGd
951773337 10.0735 good LGd
951773342 11.6127 good LGd
951773346 2.5774 noise LGd
951773350 1.16966 noise LGd
951773356 2.28124 noise LGd
951773361 6.95708 good LGd
951773368 6.06116 good LGd
951773373 9.64351 good LGd
951773378 6.23911 noise LGd
951773384 14.4246 good LGd
951773389 9.8353 good LGd
951773395 9.01181 good LGd
951773401 5.89521 good LGd
951773407 17.2197 good LGd
951773412 5.74992 good LGd
951773418 7.05133 good LGd
951773423 9.72349 good LGd
951773429 2.03365 good LGd
951773435 5.71612 good LGd
951773441 10.7019 good LGd
951773446 6.60864 good LGd
951773452 6.75145 good LGd
951773458 8.26149 good LGd
951773463 6.89054 good LGd
951773469 0.52939 good LGd
951773474 12.0999 good LGd
951773480 8.47023 good LGd
951773485 17.9799 good LGd
951773490 0.04381 noise LGd
951773496 5.71054 good LGd
951773501 10.275 good LGd
951773507 11.7831 good LGd
951773513 14.1525 good LGd
951773518 11.593 good LGd
951773523 4.68132 good LGd
951773533 7.15776 good LGd
951773538 10.1507 good LGd
951773542 4.49346 good LGd
951773548 0.31176 good LGd
951773553 8.24196 good LGd
951773560 0.00176 good LGd
951773565 13.1914 good LGd
951773570 0.0032 good LGd
951773577 8.17376 good LGd
951773582 3.94536 good LGd
951773587 10.9628 good LGd
951773594 10.7748 good LGd
951773599 0.00837 noise LGd
951773605 6.66568 good LGd
951773611 11.5895 good LGd
951773616 2.00193 good LGd
951773622 11.3103 good LGd
951773628 3.25208 good LGd
951773633 1.76239 good LGd
951773638 9.19493 good LGd
951773644 8.98805 good LGd
951773650 10.012 good LGd
951773656 8.05689 good LGd
951773662 7.08966 good LGd
951773667 2.58474 good LGd
951773673 11.9129 good LGd
951773678 14.7664 good LGd
951773683 19.4405 good LGd
951773690 12.8355 good LGd
951773696 15.4212 good LGd
951773701 4.61828 good LGd
951773706 7.06538 good LGd
951773713 10.5483 good LGd
951773718 3.08065 good LGd
951773724 0.01044 good LGd
951773730 13.4889 good LGd
951773735 1.32249 noise LGd
951773741 10.9077 good CA3
951773747 5.22662 noise CA3
951773752 2.11353 noise CA3
951773758 7.64623 good CA3
951773765 1.74875 noise CA3
951773770 4.37545 good CA3
951773775 4.7428 good CA3
951773780 2.17315 noise CA3
951773786 0.03276 good CA3
951773792 12.5212 good CA3
951773797 2.61564 noise CA3
951773803 22.0037 good CA3
951773808 4.94266 good CA3
951773813 2.64488 good CA3
951773819 1.51129 good CA3
951773824 0.10819 good CA3
951773832 0.97198 good CA3
951773838 15.3389 good CA3
951773843 0.53187 good CA3
951773849 2.82396 noise CA3
951773853 0.13124 noise CA3
951773856 1.28798 noise CA3
951773862 0.02532 noise CA3
951773869 9.21497 good CA3
951773874 0.24201 noise CA3
951773879 0.00424 good CA3
951773886 0.02842 good CA3
951773892 0.20161 good CA3
951773897 0.03121 noise CA3
951773903 32.447 noise CA3
951773908 3.27905 good CA3
951773914 20.7261 good CA3
951773920 0.06861 noise CA3
951773926 0.04051 noise CA3
951773929 0.00279 noise CA3
951773931 13.1911 good CA3
951773933 26.4001 good CA3
951773935 15.1065 good CA3
951773937 0.71911 noise CA3
951773940 2.06093 good CA3
951773943 1.61855 noise CA3
951773945 5.53167 noise CA3
951773948 11.6486 noise CA3
951773950 6.02014 good CA3
951773956 2.38127 noise CA3
951773960 1.28632 noise CA3
951773965 4.68432 good CA2
951773969 3.59402 noise CA3
951773973 2.29695 noise CA2
951773977 2.75359 noise CA2
951773982 12.0485 good CA2
951773986 8.86012 good CA1
951773990 2.37032 good CA1
951773994 4.72214 good CA1
951774002 2.18173 good CA1
951774008 3.6709 good CA1
951774013 4.5722 noise CA1
951774019 3.26014 good CA1
951774024 4.29412 good CA1
951774030 7.90808 good CA1
951774035 1.57298 good CA1
951774039 10.0113 good CA1
951774044 5.67055 good CA1
951774049 3.17148 good CA1
951774054 0.59067 good CA1
951774059 45.3328 good CA1
951774065 0.12969 good CA1
951774070 4.59214 good CA1
951774075 0.10881 good CA1
951774082 1.11096 good CA1
951774086 2.80422 good CA1
951774091 3.19235 good CA1
951774097 22.7047 good CA1
951774103 1.08368 good CA1
951774108 7.15993 good CA1
951774113 0.09548 good CA1
951774118 3.24485 good CA1
951774124 0.6009 good CA1
951774130 6.34275 good CA1
951774134 0.76086 good CA1
951774140 0.20202 good CA1
951774145 0.43752 good CA1
951774150 6.21327 good CA1
951774156 0.01261 good CA1
951774161 0.01891 good CA1
951774166 6.77511 good CA1
951774172 4.30187 good CA1
951774176 1.91233 good CA1
951774180 0.02046 good CA1
951774186 1.58507 noise CA1
951774192 1.27031 good CA1
951774197 14.1142 good CA1
951774203 2.40617 good CA1
951774208 2.43108 good CA1
951774213 8.71751 good CA1
951774220 2.89175 good CA1
951774225 3.53119 good CA1
951774231 6.2483 good CA1
951774237 0.16988 good CA1
951774242 4.82031 good CA1
951774247 24.9531 good CA1
951774253 4.07505 good CA1
951774258 0.63655 good CA1
951774264 4.27221 good CA1
951774269 1.69915 good CA1
951774275 3.28319 good CA1
951774280 0.91483 noise CA1
951774286 7.29623 noise CA1
951774290 3.97678 noise CA1
951774295 2.4254 good CA1
951774299 0.01147 noise CA1
951774304 7.5027 good CA1
951774308 13.8395 good CA1
951774313 3.97595 good CA1
951774318 4.31592 good CA1
951774322 10.2349 good CA1
951774327 5.38824 good CA1
951774331 6.53475 good CA1
951774337 30.3643 good CA1
951774341 2.66141 good CA1
951774347 1.14579 noise VISrl
951774352 1.91512 good VISrl
951774357 1.55748 noise VISrl
951774362 2.41196 noise VISrl
951774364 3.73487 good VISrl
951774368 4.57788 good VISrl
951774374 4.24442 good VISrl
951774380 5.31932 good VISrl
951774386 0.46253 noise VISrl
951774393 3.09356 good VISrl
951774401 2.91841 good VISrl
951774407 2.73168 good VISrl
951774414 2.32144 good VISrl
951774420 4.20411 good VISrl
951774427 2.8065 good VISrl
951774433 9.01998 noise VISrl
951774439 2.68983 good VISrl
951774448 10.3982 good VISrl
951774454 2.77147 good VISrl
951774461 1.37426 good VISrl
951774466 1.02964 noise VISrl
951774473 3.55062 good VISrl
951774479 3.90702 good VISrl
951774484 2.11404 noise VISrl
951774491 1.71424 good VISrl
951774502 6.93642 noise VISrl
951774507 2.62225 good VISrl
951774513 0.66073 noise VISrl
951774520 17.2249 good VISrl
951774527 0.80592 good VISrl
951774533 0.02645 good VISrl
951774538 0.09207 noise VISrl
951774544 0.11501 noise VISrl
951774549 1.59003 good VISrl
951774555 0.01447 good VISrl
951774562 2.70048 good VISrl
951774567 2.73571 good VISrl
951774572 2.62421 good VISrl
951774576 3.32142 good VISrl
951774582 1.86366 good VISrl
951774588 10.9189 good VISrl
951774592 18.9308 good VISrl
951774598 3.77403 noise VISrl
951774603 5.37553 good VISrl
951774609 1.08079 good VISrl
951774614 9.83375 good VISrl
951774620 8.5343 good VISrl
951774625 2.47717 good VISrl
951774631 8.54856 good VISrl
951774636 17.9195 good VISrl
951774641 0.00083 good VISrl
951774648 13.007 good VISrl
951774653 11.9066 good VISrl
951774659 7.84381 good VISrl
951774664 9.02308 good VISrl
951774670 2.4595 good VISrl
951774676 8.36369 good VISrl
951774682 3.01792 good VISrl
951774686 2.36773 good VISrl
951774692 5.19159 good VISrl
951774697 3.62357 good VISrl
951774704 2.26626 good VISrl
951774708 2.1035 good VISrl
951774713 3.15867 good VISrl
951774719 2.25675 good VISrl
951774724 4.8387 noise VISrl
951774730 15.427 good VISrl
951774736 8.75523 good VISrl
951774741 1.59148 good VISrl
951774745 4.33163 good VISrl
951774752 7.80909 good VISrl
951774757 1.71279 good VISrl
951774761 2.3604 good VISrl
951774768 3.21633 good VISrl
951774772 1.79246 good VISrl
951774777 5.85552 good VISrl
951774783 1.22463 good VISrl
951774785 3.60363 good VISrl
951774791 3.0265 noise VISrl
951774796 2.2892 good VISrl
951774800 1.44009 noise VISrl
951774806 3.8847 good VISrl
951774812 0.85417 good VISrl
951774817 1.44153 good VISrl
951774823 0.06531 noise VISrl
951774827 0.51503 good VISrl
951774832 0.86151 good VISrl
951774838 0.71219 good VISrl
951774845 5.84715 good VISrl
951774850 1.69874 good VISrl
951774856 3.67338 noise VISrl
951774862 2.26429 noise VISrl
951774866 2.56294 noise VISrl
951774872 3.04841 good VISrl
951774878 3.83149 good VISrl
951774884 0.12938 good VISrl
951774890 0.00176 noise
951774895 8.19463 noise
951774900 2.1871 noise
951774906 0.01126 noise
951774913 2.63393 noise
951774918 0.81625 noise
951774924 0.00496 good VPM
951774930 8.73084 good VPM
951774934 21.6061 good VPM
951774941 0.55357 good VPM
951774947 6.24169 good LGd
951774952 10.4657 good LGd
951774958 9.37008 good LGd
951774963 3.82084 good LGd
951774969 0.28262 good LGd
951774975 0.0279 good CA3
951774982 0.05735 good CA3
951774988 0.00372 good CA3
951774995 0.30174 good CA3
951775003 0.02325 good CA3
951775009 0.07079 good CA1
951775014 0.07823 good CA1
951775020 0.50676 good VISrl
951775028 0.01891 good VISrl
951775033 0.43236 good VISrl
951775039 0.07451 good VISrl
951775044 0.03813 good VISrl
951775051 0.21969 good VISrl
951775057 0.85789 good VISrl
951775065 2.42664 good VISrl
951775073 0.41376 good VISrl
951775080 0.1362 noise
951775086 0.01912 good CA3
951775092 0.03048 good VISrl
951775099 0.01653 good LGd
951775105 0.0124 good LGd
951775110 0.02656 good CA1
951775116 0.26196 good VISrl
951775173 5.91525 good PO
951775180 7.71454 good PO
951775184 3.89483 good Eth
951775192 9.07888 good PO
951775198 3.91622 good Eth
951775206 8.11248 good Eth
951775212 2.37393 good Eth
951775218 8.28102 good Eth
951775223 7.29561 good Eth
951775230 5.32149 good Eth
951775236 8.77363 good Eth
951775243 4.58635 good Eth
951775249 2.43449 good Eth
951775254 4.44902 good Eth
951775260 5.00383 good Eth
951775265 4.27996 good Eth
951775271 10.4868 good Eth
951775279 7.32362 good Eth
951775285 11.3536 good Eth
951775292 7.47914 good Eth
951775297 3.22563 good Eth
951775303 4.19481 good Eth
951775309 10.7328 good Eth
951775314 7.63786 good Eth
951775321 5.68471 good Eth
951775327 9.05005 good Eth
951775333 4.2221 good Eth
951775339 7.25025 good Eth
951775345 2.67268 good Eth
951775351 1.50984 good Eth
951775355 3.66739 good Eth
951775363 10.0034 good Eth
951775369 4.31685 good Eth
951775375 6.58642 good Eth
951775380 11.8742 good Eth
951775385 4.25516 good Eth
951775392 12.3145 good Eth
951775397 3.13004 good Eth
951775403 2.64674 good Eth
951775407 2.80278 good Eth
951775412 11.3512 good Eth
951775417 5.77244 good Eth
951775423 3.63814 good Eth
951775429 8.45359 good Eth
951775435 0.12783 good Eth
951775441 15.7157 good Eth
951775448 5.67954 good Eth
951775453 2.09172 noise Eth
951775465 3.09677 good Eth
951775472 1.61307 good Eth
951775477 4.29391 good Eth
951775484 2.01732 good Eth
951775489 2.53524 good Eth
951775496 3.5313 good Eth
951775502 8.72495 good Eth
951775508 0.58591 good Eth
951775515 7.21904 good Eth
951775522 4.06905 good Eth
951775529 9.18253 good Eth
951775535 4.03723 good Eth
951775542 0.60586 noise Eth
951775550 12.0122 good Eth
951775556 17.1874 good Eth
951775561 0.58271 good Eth
951775569 7.29985 good Eth
951775576 6.64046 good Eth
951775582 11.2056 good Eth
951775589 3.70862 good Eth
951775595 8.77259 good Eth
951775602 0.10995 good Eth
951775607 8.06443 good Eth
951775614 6.70484 good Eth
951775620 5.07875 good Eth
951775627 0.02242 good Eth
951775633 11.1431 good Eth
951775639 5.2942 good Eth
951775645 6.28933 good Eth
951775648 11.3501 good Eth
951775655 4.79406 good Eth
951775660 9.35944 good Eth
951775666 11.0597 good Eth
951775671 8.41691 good Eth
951775678 3.69808 good Eth
951775684 2.12748 good Eth
951775689 13.6246 good Eth
951775695 1.63064 good Eth
951775702 14.4631 good Eth
951775708 15.7992 good Eth
951775714 3.70376 good Eth
951775720 5.57476 good Eth
951775726 9.92344 good Eth
951775733 0.47348 good Eth
951775738 1.0131 good Eth
951775741 4.01666 good Eth
951775745 9.23078 good Eth
951775748 3.94433 good Eth
951775751 6.06096 good LP
951775754 6.40713 good LP
951775759 4.98223 good LP
951775764 3.11888 good LP
951775770 12.4008 good LP
951775776 4.19047 good LP
951775782 4.02462 good LP
951775789 0.05745 good LP
951775795 9.85834 good LP
951775800 0.03658 good LP
951775806 4.49077 good LP
951775813 1.23269 good LP
951775819 0.663 good LP
951775826 7.01712 good LP
951775830 0.03823 good LP
951775836 1.6696 good LP
951775843 5.1145 good LP
951775849 1.22205 good LP
951775857 1.93197 good LP
951775863 2.86612 good LP
951775869 2.13171 good LP
951775875 6.9637 good LP
951775880 0.03751 good LP
951775885 0.56607 good LP
951775890 9.40997 good LP
951775897 7.1681 good LP
951775903 7.18907 noise LP
951775908 10.2125 good LP
951775915 7.01413 good LP
951775919 2.94631 good LP
951775927 6.76664 good LP
951775934 3.88078 good LP
951775940 4.93687 good LP
951775947 6.44878 good LP
951775954 1.10311 good LP
951775961 3.56591 good LP
951775967 3.97533 good LP
951775974 4.69145 good LP
951775980 6.49197 good LP
951775985 4.92654 good LP
951775990 4.2006 good LP
951776000 1.76766 noise CA1
951776007 2.56934 noise LP
951776014 0.04764 noise LP
951776020 2.06269 good LP
951776024 3.81785 good LP
951776031 8.76536 good LP
951776037 10.8718 good LP
951776043 1.12409 good LP
951776049 4.25723 good LP
951776055 5.59956 good LP
951776061 2.47872 good LP
951776067 4.50431 good LP
951776074 4.13591 good LP
951776080 6.05755 good LP
951776085 3.87726 good LP
951776091 3.25219 good LP
951776096 3.20424 good LP
951776100 2.1993 good LP
951776106 0.33336 noise LP
951776112 1.66009 noise LP
951776117 28.7194 good LP
951776124 2.19186 good LP
951776129 0.12648 good LP
951776135 7.08915 good LP
951776142 6.08607 good LP
951776147 12.7011 good LP
951776152 1.01786 good LP
951776159 1.14196 good LP
951776165 2.34851 noise LP
951776170 1.31237 noise LP
951776176 0.01395 good LP
951776182 2.65387 good TH
951776188 7.58506 good TH
951776194 1.39235 noise DG
951776200 3.31594 noise DG
951776206 2.21232 noise DG
951776213 3.47467 good DG
951776217 1.15323 noise DG
951776225 2.83533 noise DG
951776231 1.63539 good DG
951776237 4.36801 good DG
951776243 0.02015 noise DG
951776249 0.1333 good DG
951776255 0.86006 good DG
951776262 1.76591 good DG
951776268 0.69349 good DG
951776273 2.10133 good DG
951776281 2.41527 good DG
951776286 5.27199 good DG
951776292 0.29006 good DG
951776299 2.34386 noise DG
951776306 3.13056 noise DG
951776311 0.47865 noise DG
951776317 2.72466 noise DG
951776323 0.41438 noise DG
951776329 0.17257 good DG
951776333 3.40068 noise DG
951776339 2.95179 good DG
951776345 5.67582 good DG
951776352 0.08835 noise DG
951776358 1.60532 noise DG
951776364 3.15164 noise CA1
951776370 2.33405 noise CA1
951776376 1.21916 noise DG
951776382 1.59633 noise DG
951776388 2.31338 noise CA1
951776394 3.37784 noise CA1
951776401 0.3811 noise CA1
951776407 1.67166 good CA1
951776412 2.13885 good CA1
951776419 2.17935 noise CA1
951776425 3.04179 good CA1
951776431 25.9364 good CA1
951776436 16.3894 good CA1
951776442 0.89551 noise CA1
951776449 0.88187 noise CA1
951776455 4.70261 good CA1
951776462 2.2024 noise CA1
951776468 0.30908 noise CA1
951776475 5.13217 good CA1
951776480 0.34979 good CA1
951776486 11.6435 good CA1
951776493 3.33826 noise CA1
951776499 2.7602 noise CA1
951776505 1.7409 noise CA1
951776512 3.64651 noise CA1
951776518 1.70142 noise CA1
951776524 0.23643 good CA1
951776530 2.69469 noise CA1
951776541 2.25727 noise CA1
951776547 2.07664 noise CA1
951776551 0.64513 good CA1
951776556 3.84606 noise CA1
951776563 2.90591 good CA1
951776569 4.88251 good CA1
951776576 0.00723 good CA1
951776582 0.00858 noise CA1
951776589 1.49506 good CA1
951776595 0.3068 good CA1
951776599 1.85973 noise CA1
951776606 0.05828 noise CA1
951776612 0.34556 noise CA1
951776618 2.53968 good CA1
951776624 9.47982 good CA1
951776630 3.25229 good CA1
951776636 3.49523 good CA1
951776642 1.51511 noise CA1
951776647 3.67679 noise CA1
951776653 5.73586 noise CA1
951776660 2.62494 good CA1
951776666 1.85581 good CA1
951776671 7.42644 good CA1
951776677 0.02563 good CA1
951776683 1.38026 good CA1
951776690 0.38668 good CA1
951776697 3.73518 good CA1
951776703 5.1762 good CA1
951776710 0.80106 good CA1
951776716 4.67522 good CA1
951776723 2.30098 good CA1
951776731 0.20771 good CA1
951776737 10.9451 good CA1
951776743 11.8429 good CA1
951776748 1.14434 good CA1
951776753 5.10355 good CA1
951776760 6.08576 good CA1
951776767 16.1401 good CA1
951776772 2.8405 good CA1
951776776 3.27616 good CA1
951776781 5.68213 noise CA1
951776789 4.30807 good CA1
951776794 1.27733 good CA1
951776799 4.62221 good CA1
951776806 3.71358 good CA1
951776812 4.75965 good CA1
951776818 5.79559 good CA1
951776824 1.50478 good CA1
951776832 4.22158 good CA1
951776838 8.0572 good CA1
951776845 0.01095 noise CA1
951776852 2.96067 good CA1
951776857 0.6226 good CA1
951776864 3.84451 good CA1
951776869 27.6137 good CA1
951776877 4.8419 good CA1
951776884 1.78947 good CA1
951776888 4.99505 good CA1
951776896 7.33798 good CA1
951776902 1.86769 noise CA1
951776909 4.72844 noise CA1
951776914 1.52307 noise CA1
951776922 7.57958 good CA1
951776927 2.80154 good CA1
951776932 1.71186 noise CA1
951776939 8.60229 good CA1
951776944 12.1399 good CA1
951776950 0.62704 good VISpm
951776956 0.55915 noise VISpm
951776962 1.88547 noise VISpm
951776968 0.07606 noise VISpm
951776973 5.24429 good VISpm
951776980 0.49395 noise VISpm
951776985 2.14122 good VISpm
951776991 1.7595 good VISpm
951776998 15.5874 good VISpm
951777003 0.02139 good VISpm
951777009 2.26564 good VISpm
951777016 7.24705 good VISpm
951777021 6.45084 good VISpm
951777029 2.72641 good VISpm
951777034 0.00124 noise VISpm
951777040 1.73635 noise VISpm
951777046 3.54597 good VISpm
951777052 13.0328 good VISpm
951777058 0.75921 good VISpm
951777065 1.94437 good VISpm
951777071 1.55035 good VISpm
951777079 2.82437 good VISpm
951777092 4.38795 good VISpm
951777098 16.4999 good VISpm
951777105 1.70287 good VISpm
951777112 6.41085 good VISpm
951777117 4.244 good VISpm
951777123 7.17006 good VISpm
951777129 12.4829 good VISpm
951777136 9.09128 good VISpm
951777142 10.2364 good VISpm
951777148 5.99234 good VISpm
951777155 4.41244 good VISpm
951777162 5.94036 good VISpm
951777168 8.81382 good VISpm
951777175 4.78135 good VISpm
951777181 6.2388 good VISpm
951777188 9.04302 good VISpm
951777193 0.42626 noise VISpm
951777199 6.21296 good VISpm
951777205 2.5617 good VISpm
951777212 8.14979 good VISpm
951777218 8.29714 good VISpm
951777223 4.54461 good VISpm
951777227 5.30526 noise VISpm
951777232 4.30135 good VISpm
951777237 1.81179 good VISpm
951777243 0.69834 good VISpm
951777249 3.40781 good VISpm
951777257 1.51222 good VISpm
951777263 3.24774 good VISpm
951777270 1.99283 good VISpm
951777275 1.71165 noise VISpm
951777281 2.62432 good VISpm
951777287 3.70531 good VISpm
951777292 6.32219 good VISpm
951777298 2.21759 good VISpm
951777304 2.35492 good VISpm
951777310 0.00692 noise VISpm
951777315 0.85717 good VISpm
951777321 5.74124 noise VISpm
951777323 1.19601 noise
951777326 7.5492 noise
951777329 3.32462 good Eth
951777333 2.34583 good Eth
951777335 8.80669 good Eth
951777339 6.94045 good Eth
951777342 9.22283 good Eth
951777345 3.64734 good Eth
951777348 5.85966 good Eth
951777351 2.74057 good Eth
951777355 0.02976 good Eth
951777360 3.54401 good Eth
951777366 2.21697 good LP
951777371 2.06393 good LP
951777377 0.0216 good LP
951777384 1.97764 good LP
951777389 4.77825 good LP
951777395 2.48264 good LP
951777401 0.57599 good LP
951777406 9.18087 good LP
951777413 0.03513 good LP
951777419 3.67266 good LP
951777424 1.44453 good LP
951777430 3.33051 good LP
951777437 0.24656 good LP
951777442 0.98799 good LP
951777448 1.35814 good LP
951777455 0.37707 good LP
951777462 0.18022 good DG
951777468 0.05012 good DG
951777474 0.03069 good DG
951777480 0.06975 good DG
951777485 0.40177 noise DG
951777492 0.04919 good CA1
951777499 0.24739 noise CA1
951777504 0.42574 good CA1
951777511 0.13516 good CA1
951777517 0.09641 good CA1
951777523 1.61256 good CA1
951777528 0.82524 noise VISpm
951777534 0.03792 good VISpm
951777540 0.1177 good VISpm
951777548 0.20078 noise VISpm
951777553 2.35957 good LP
951777559 0.02108 good LP
951777565 0.08143 noise DG
951777571 0.20088 good VISpm
951777576 0.01085 good LP
951777582 0.1457 good CA1
951777593 0.0464 good CA1
951777600 0.0621 good CA1
Extracting trial structure#
Mice were exposed to a series of stimuli (gabor patches, flashes, natural images, etc.), out of which we are exclusively interested in flashes presentation for this tutorial.
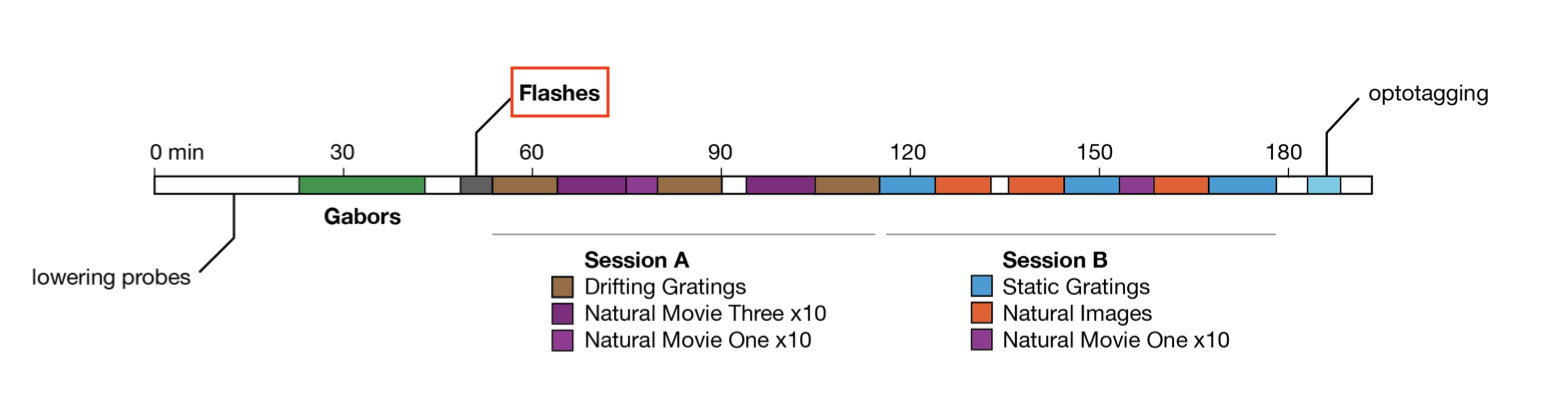
During the flashes presentation trials, mice were exposed to white or black full-field flashes in a gray background, each lasting 250 ms, and separated by a 2 second inter-trial interval. In total, they were exposed to 150 flashes (75 black, 75 white).
# Extract flashes as an Interval Set object
flashes = data["flashes_presentations"]
# Remove unnecessary columns, similarly to above
cols_to_keep = ['color']
restrict_cols(cols_to_keep, flashes)
print(flashes)
index start end color
0 1285.600869922 1285.851080039 -1.0
1 1287.602559922 1287.852767539 -1.0
2 1289.604229922 1289.854435039 -1.0
3 1291.605889922 1291.856100039 -1.0
4 1293.607609922 1293.857807539 1.0
5 1295.609249922 1295.859455039 -1.0
6 1297.610959922 1297.861155039 1.0
... ... ... ...
143 1571.840009922 1572.090212539 -1.0
144 1573.841669922 1574.091877539 1.0
145 1575.843359922 1576.093562539 1.0
146 1577.845019922 1578.095227539 -1.0
147 1579.846709922 1580.096915039 1.0
148 1581.848389922 1582.098595039 1.0
149 1583.850039922 1584.100247539 -1.0
shape: (150, 2), time unit: sec.
Create an object for white and a separate object for black flashes
flashes_white = flashes[flashes["color"] == "1.0"]
flashes_black = flashes[flashes["color"] == "-1.0"]
Show code cell source
def plot_stimuli():
n_flashes = 5
n_seconds = 13
offset = .5
start = data["flashes_presentations"]["start"].min() - offset
end = start + n_seconds
fig, ax = plt.subplots(figsize = (17, 4))
[ax.axvspan(s, e, color = "silver", alpha=.4, ec="black") for s, e in zip(flashes_white[:n_flashes].start, flashes_white[:n_flashes].end)]
[ax.axvspan(s, e, color = "black", alpha=.4, ec="black") for s, e in zip(flashes_black[:n_flashes].start, flashes_black[:n_flashes].end)]
plt.xlabel("Time (s)")
plt.ylabel("Absent = 0, Present = 1")
ax.set_title("Stimuli presentation")
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
plt.xlim(start-.1,end)
plt.show()
And we can plot the stimuli
plot_stimuli()
To analyze how units’ activity evolves around the time of stimulus presentation, we can extend each stimulus interval to include some time before and after the flash. Specifically, we add 500 ms before the flash onset and 500 ms after the flash offset. This gives us a window that captures pre-stimulus baseline activity and any delayed neural responses.
dt = .50 # 500 ms
start = flashes.start - dt # Start 500 ms before stimulus presentation
end = flashes.end + dt # End 500 ms after stimulus presentation
extended_flashes = nap.IntervalSet(start,end, metadata=flashes.metadata)
print(extended_flashes)
index start end color
0 1285.100869922 1286.351080039 -1.0
1 1287.102559922 1288.352767539 -1.0
2 1289.104229922 1290.354435039 -1.0
3 1291.105889922 1292.356100039 -1.0
4 1293.107609922 1294.357807539 1.0
5 1295.109249922 1296.359455039 -1.0
6 1297.110959922 1298.361155039 1.0
... ... ... ...
143 1571.340009922 1572.590212539 -1.0
144 1573.341669922 1574.591877539 1.0
145 1575.343359922 1576.593562539 1.0
146 1577.345019922 1578.595227539 -1.0
147 1579.346709922 1580.596915039 1.0
148 1581.348389922 1582.598595039 1.0
149 1583.350039922 1584.600247539 -1.0
shape: (150, 2), time unit: sec.
This extended IntervalSet, extended_flashes, will later allow us to restrict units’ activity to the periods surrounding each flash stimulus.
We now create one object for white and another for black extended flashes.
extended_flashes_white = extended_flashes[extended_flashes["color"]=="1.0"]
extended_flashes_black = extended_flashes[extended_flashes["color"]=="-1.0"]
Preprocessing spiking data#
There are multiple reasons for filtering units. Here, we will use four criteria: brain area, quality of units, firing rate and responsiveness
Brain area: we are interested in analyzing VISp units for this tutorial
Quality: we will only select “good” quality units
Firing rate: overall, we want units with a firing rate larger than 2Hz around the presentation of stimuli
Responsiveness: for the purposes of the tutorial, we will select the most responsive units (top 15%), and only use those for further analysis. We define responsiveness as the normalized difference between post stimulus and pre stimulus average firing rate.
What does it mean for a unit to be of “good” quality?
More information on unit quality metrics can be found in Visualizing Unit Quality Metrics
# Filter units according criteria 1 & 2
units = units[
(units["brain_area"]=="VISp") &
(units["quality"]=="good")
]
# Restrict around stimuli presentation
units = units.restrict(extended_flashes)
# Filter according to criterion 3
units = units[(units["rate"]>2.0)]
print(units)
Index rate quality brain_area
--------- -------- --------- ------------
951765440 2.32495 good VISp
951765454 22.6523 good VISp
951765460 2.29829 good VISp
951765467 25.8091 good VISp
951765485 22.9616 good VISp
951765547 2.83687 good VISp
951765552 5.69507 good VISp
951765557 6.87888 good VISp
951765582 16.7119 good VISp
951765594 2.98618 good VISp
951765606 4.04201 good VISp
951765611 31.0989 good VISp
951765623 8.47862 good VISp
951765653 7.81739 good VISp
951765661 14.579 good VISp
951765666 5.01251 good VISp
951765669 6.92687 good VISp
951765675 18.9142 good VISp
951765681 14.8242 good VISp
951765686 11.4915 good VISp
951765692 2.57025 good VISp
951765697 5.22048 good VISp
951765716 2.10632 good VISp
951765721 8.19066 good VISp
951765727 9.74774 good VISp
951765732 4.31929 good VISp
951765737 6.79356 good VISp
951765769 8.68658 good VISp
951765793 4.4846 good VISp
951765809 5.36979 good VISp
951765820 5.92437 good VISp
951765886 2.35695 good VISp
951768133 2.24497 good VISp
951768139 6.75623 good VISp
951768154 2.82087 good VISp
951768183 6.07367 good VISp
951768188 5.18849 good VISp
951768222 41.124 good VISp
951768247 10.121 good VISp
951768278 3.43944 good VISp
951768285 4.06867 good VISp
951768291 2.77821 good VISp
951768298 7.65208 good VISp
951768307 2.32495 good VISp
951768318 8.25998 good VISp
951768327 3.33812 good VISp
951768332 31.4509 good VISp
951768345 20.5566 good VISp
951768369 9.82773 good VISp
951768374 10.9315 good VISp
951768390 25.5692 good VISp
951768402 6.98553 good VISp
951768408 11.6461 good VISp
951768421 13.4538 good VISp
951768427 5.65774 good VISp
951768434 11.6514 good VISp
951768441 25.7291 good VISp
951768446 9.42779 good VISp
951768451 13.9231 good VISp
951768457 5.48177 good VISp
951768462 2.36761 good VISp
951768473 5.15649 good VISp
951768480 8.93187 good VISp
951768495 14.9895 good VISp
951768500 9.82773 good VISp
951768524 2.2183 good VISp
951768550 3.96735 good VISp
951768557 3.92469 good VISp
951768568 13.7737 good VISp
951768581 2.61291 good VISp
951768586 2.82087 good VISp
951768604 3.54076 good VISp
951768621 3.41278 good VISp
951768627 12.3766 good VISp
951768632 5.93503 good VISp
951768649 4.22864 good VISp
951768673 2.39428 good VISp
951768705 7.49744 good VISp
951768712 4.48993 good VISp
951768723 2.77288 good VISp
951768749 2.04767 good VISp
951768754 2.76755 good VISp
951768766 11.3208 good VISp
951768793 6.27098 good VISp
951768815 2.23963 good VISp
951768823 5.40712 good VISp
951768830 7.58276 good VISp
951768835 5.60442 good VISp
951768881 4.01534 good VISp
951768894 4.2713 good VISp
951769295 2.23963 good VISp
951769344 2.91152 good VISp
Now, to calculate responsiveness, we need to do some preprocessing to align units’ spiking timestamps with the onset of the stimulus repetitions, and then take an average over them. For this, we will use the compute_perievent function, which allows us to re-center time series and timestamps around particular events and compute spikes-triggered averages.
# Set window of perievent 500 ms before and after the start of the event
window_size = (-.250, .500)
# Re-center timestamps for white stimuli
# +50 because we subtracted 500 ms at beginning of stimulus presentation
peri_white = nap.compute_perievent(timestamps = units,
tref = nap.Ts(extended_flashes_white.start +.50),
minmax = window_size
)
# Re-center timestamps for black stimuli
# +50 because we subtracted 500 ms at beginning of stimulus presentation
peri_black = nap.compute_perievent(timestamps = units,
tref = nap.Ts(extended_flashes_black.start +.50),
minmax = window_size
)
The output of the perievent is a dictionary of TsGroup objects, indexed by each unit ID.
Will the output of compute_perievent always be a dictionary?
No. In this case it is because the input was a TsGroup containing the spiking information of multiple units. Had it been a Ts/Tsd/TsdFrame/TsdTensor (only one unit), then the output of compute_perievent would have been a TsGroup.
For more information, please refer to Pynapple documentation for processing perievents.
When we index an element of this dictionary, we retrieve the spike times aligned to stimulus onset for a single unit, across all repetitions of the stimulus. These spike times are centered around the stimulus within the specified window_size. You’ll notice that the ref_times in the perievent output correspond exactly to the start times of the stimulus presentations!
# Let's select one unit
example_id = 951765485
print(f"Number of trials: {len(peri_black[example_id])}\n ")
# And print it's rates
print(f"TsGroup of centered activity for unit {example_id}: \n {peri_black[example_id]}\n")
# Start times of black flashes presentation
print(f"black flashes start times: \n {flashes_black.starts}")
Number of trials: 75
TsGroup of centered activity for unit 951765485:
Index rate ref_times
------- -------- -----------
0 18.6667 1285.6
1 18.6667 1287.6
2 12 1289.6
3 9.33333 1291.61
4 32 1295.61
5 20 1303.62
6 18.6667 1307.62
7 22.6667 1311.62
8 32 1323.63
9 24 1327.64
10 33.3333 1331.64
11 10.6667 1333.64
12 17.3333 1335.64
13 21.3333 1349.65
14 44 1353.66
15 34.6667 1355.66
16 12 1363.67
17 26.6667 1367.67
18 10.6667 1369.67
19 16 1371.67
20 22.6667 1377.68
21 33.3333 1379.68
22 17.3333 1381.68
23 18.6667 1385.68
24 12 1387.69
25 17.3333 1391.69
26 33.3333 1393.69
27 29.3333 1395.69
28 28 1399.7
29 25.3333 1403.7
30 24 1407.7
31 13.3333 1417.71
32 29.3333 1421.71
33 24 1423.72
34 20 1425.72
35 26.6667 1429.72
36 16 1435.73
37 21.3333 1437.73
38 21.3333 1443.73
39 13.3333 1447.74
40 13.3333 1451.74
41 32 1455.74
42 20 1457.74
43 22.6667 1459.75
44 30.6667 1463.75
45 16 1465.75
46 9.33333 1467.75
47 20 1469.75
48 12 1471.76
49 30.6667 1479.76
50 17.3333 1481.76
51 20 1485.77
52 13.3333 1499.78
53 16 1503.78
54 17.3333 1505.78
55 18.6667 1507.79
56 10.6667 1515.79
57 4 1517.79
58 33.3333 1523.8
59 10.6667 1525.8
60 8 1527.8
61 16 1529.8
62 6.66667 1535.81
63 6.66667 1541.81
64 9.33333 1543.82
65 14.6667 1545.82
66 12 1555.83
67 12 1559.83
68 13.3333 1561.83
69 6.66667 1563.83
70 8 1565.83
71 12 1569.84
72 20 1571.84
73 12 1577.85
74 10.6667 1583.85
black flashes start times:
Time (s)
1285.600869922
1287.602559922
1289.604229922
1291.605889922
1295.609249922
1303.615919922
1307.619279922
...
1561.831629922
1563.833279922
1565.834999922
1569.838349922
1571.840009922
1577.845019922
1583.850039922
shape: 75
Let’s inspect a bit further our TsGroup objects with the centered spikes. If we grab the FIRST element of peri_black[example_id], we would get the spike times centered around the FIRST presentation of stimulus.
print(peri_black[example_id][0])
Time (s)
-0.128226254
-0.12362626
0.070806812
0.132140063
0.223106608
0.252739902
0.270706544
0.305906497
0.308506494
0.330173131
0.401073036
0.434739658
0.455372963
0.471839608
shape: 14
Negative spike times are expected here because the spike times in peri_white and peri_black are aligned relative to stimulus onset. A negative time means the spike occurred before the stimulus was presented, while a positive time indicates the spike occurred after stimulus onset. This alignment allows us to analyze how neuronal activity changes around the time of stimulus presentation.
We can also visualize these aligned spike times to better understand the timing and rate of neural responses relative to the stimulus. This type of plot is known as a Peristimulus Time Histogram (PSTH), and it shows how spiking activity is distributed around the stimulus onset. Let’s generate a PSTH for the first 9 units to explore their response patterns.
Show code cell source
def plot_raster_psth(peri_color, units, color_flashes, bin_size, n_units = 9, smoothing=0.015):
"""
Plot perievent time histograms (PSTHs) and raster plots for multiple units.
Parameters:
-----------
peri_color : dict
Dictionary mapping unit names to binned spike count peri-stimulus data (e.g., binned time series).
units : dict
Dictionary of neural units, e.g., spike trains or trial-aligned spike events.
color_flashes : str
A label indicating the flash color condition ('black' or other), used for visual styling.
bin_size : float
Size of the bin used for spike count computation (in seconds).
smoothing : float
Standard deviation for Gaussian smoothing of the PSTH traces.
"""
# Layout setup: 9 columns (units), 2 rows (split vertically into PSTH and raster plot)
n_cols = n_units
n_rows = 2
fig, ax = plt.subplots(n_rows, n_cols)
fig.set_figheight(4)
fig.set_figwidth(17)
fig.tight_layout()
# Use tab10 color palette for plotting different units
colors = plt.cm.tab10.colors[:n_cols]
# Extract unit names for iteration
units_list = list(units.keys())
start = 0
end = int(n_rows / 2) # Plot as many units as half the number of rows
# each unit occupies 2 rows (one for psth and other for raster)
for col in range(n_cols):
for i, unit in enumerate(units_list[start:end]):
u = peri_color[unit]
line_color = colors[col]
# Plot PSTH (smoothed firing rate)
ax[2*i, col].plot(
(np.mean(u.count(bin_size), 1) / bin_size).smooth(std=smoothing),
linewidth=2,
color=line_color
)
ax[2*i, col].axvline(0.0) # Stimulus onset line
span_color = "black" if color_flashes == "black" else "silver"
ax[2*i, col].axvspan(0, 0.250, color=span_color, alpha=0.3, ec="black") # Stim duration
ax[2*i, col].set_xlim(-0.25, 0.50)
ax[2*i, col].set_title(f'{unit}')
# Plot raster
ax[2*i+1, col].plot(u.to_tsd(), "|", markersize=1, color=line_color, mew=2)
ax[2*i+1, col].axvline(0.0)
ax[2*i+1, col].axvspan(0, 0.250, color=span_color, alpha=0.3, ec="black")
ax[2*i+1, col].set_ylim(0, 75)
ax[2*i+1, col].set_xlim(-0.25, 0.50)
# Shift window for next units
start += 1
end += 1
# Y-axis and title annotations
ax[0, 0].set_ylabel("Rate (Hz)")
ax[1, 0].set_ylabel("Trial")
if n_rows > 2:
ax[2, 0].set_ylabel("Rate (Hz)")
ax[3, 0].set_ylabel("Trial")
fig.text(0.5, 0.00, 'Time from stim(s)', ha='center')
fig.text(0.5, 1.00, f'PSTH & Spike Raster Plot - {color_flashes} flashes', ha='center')
bin_size = 0.005 # Bin size
# Plot PSTH and spike raster plots
plot_raster_psth(peri_white, units, "white", bin_size)
plot_raster_psth(peri_black, units, "black", bin_size)
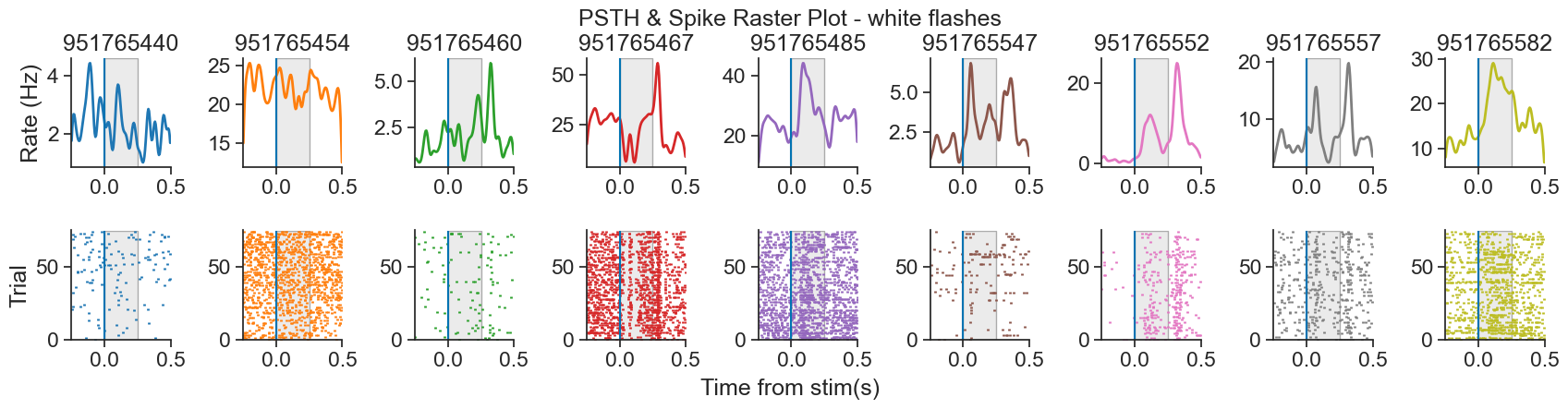
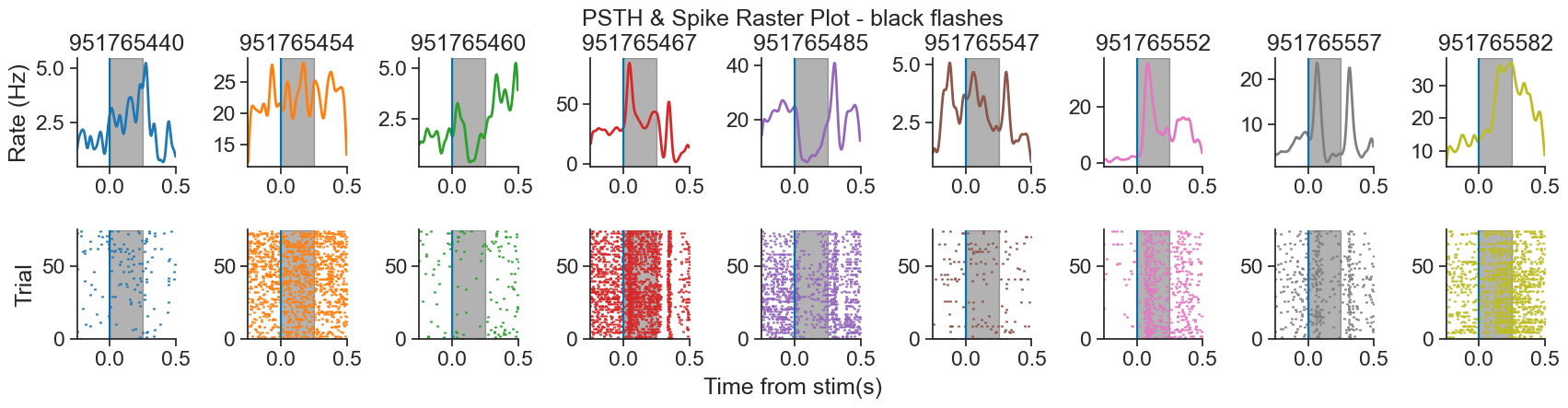
How to choose bin size?
The bin_size determines the width of the time bins used to discretize the spike train. For example, a bin size of 0.005 means each second is divided into 200 bins of 5 milliseconds each. Smaller bin sizes provide higher temporal resolution, allowing you to detect rapid changes in firing rate, while larger bin sizes smooth out the activity over time but may obscure fine temporal dynamics.
In this tutorial, we use a bin size of 0.005, but there is no one-size-fits-all rule. The optimal bin size depends on the timescale of the neural activity you are modeling. For fast, precisely timed responses, a small bin size may be necessary. For slower or more sustained responses, larger bins may be more appropriate. Ultimately, it’s a modeling decision that should balance resolution with interpretability and noise.
Why does the PSTH plot look so smooth?
We are using the smooth function from Pynapple to apply Gaussian smoothing to the perievent time series before plotting. This reduces trial-to-trial variability and emphasizes consistent temporal patterns in firing rate, making features like peaks or latency shifts easier to interpret—especially when spike trains are noisy or sparse.
In this tutorial, we use a Gaussian kernel with a standard deviation of 0.015 seconds.
To convert the standard deviation from seconds to bins, we divide by the bin size:
\( \begin{aligned} \frac{0.015}{0.005} = 3 \text{ bins} \end{aligned} \)
For implementation details, refer to the Pynapple documentation.
In the plot above, we can see that some units (951765552, pink or 951765557, gray) are clearly more responsive than others (951765454, orange), which are apparently not modulated by the flashes. Thus, it would make sense to take a subset of the neurons, the most responsive ones, and model those.
We will now calculate responsiveness for each neuron as the normalized difference between average firing rate before and after stimulus presentation, and select the most responsive ones for further analyses.
Show code cell source
def get_responsiveness(perievents, bin_size):
"""Calculate responsiveness for each neuron. This is
computer as:
post_presentation_avg :
Average firing rate during presentation (250 ms) of stimulus across
all instances of stimulus.
pre_presentation_avg :
Average firing rate prior (250 ms) to the presentation of stimulus
across all instances prior of stimulus.
responsiveness :
abs((post_presentation_avg - pre_presentation_avg) / (post_presentation_avg + pre_presentation_avg))
Larger values indicate higher responsiveness to the stimuli.
Parameters
----------
perievents : TsGroup
Contains perievent information of a subset of neurons
bin_size : float
Bin size for calculating spike counts
Returns
----------
resp_array : np.array
Array of responsiveness information.
resp_dict : dict
Dictionary of responsiveness information. Indexed by each neuron's,
contains responsiveness, pre_presentation_avg and post_presentation_avg information
"""
resp_dict = {}
resp_array = np.zeros(len(perievents.keys()), dtype=float)
for index,unit in enumerate(perievents.keys()):
# Count the number of timestamps in each bin_size bin.
peri_counts = perievents[unit].count(bin_size)
# Get the firing rate
peri_rate = peri_counts/bin_size
# Compute average firing rate for each millisecond in the
# the 250 ms before stimulus presentation
pre_presentation = np.mean(peri_rate,1).restrict(nap.IntervalSet([-.25,0]))
# Compute average firing rate for each millisecond in the
# the 250 ms after stimulus presentation
post_presentation = np.mean(peri_rate,1).restrict(nap.IntervalSet([0,.25]))
pre_presentation_avg = np.mean(pre_presentation)
post_presentation_avg = np.mean(post_presentation)
responsiveness = abs((post_presentation_avg - pre_presentation_avg) / (post_presentation_avg + pre_presentation_avg))
resp_dict[unit] = {
"responsiveness": responsiveness,
"pre_presentation_avg": pre_presentation_avg,
"post_presentation_avg": post_presentation_avg,
}
resp_array[index] = responsiveness
return resp_array, resp_dict
# Calculate responsiveness
responsiveness_white,_ = get_responsiveness(peri_white, bin_size)
responsiveness_black,_ = get_responsiveness(peri_black, bin_size)
# Add responsiveness as metadata for units
units.set_info(responsiveness_white=responsiveness_white)
units.set_info(responsiveness_black=responsiveness_black)
# See metadata
print(units)
Index rate quality brain_area responsiveness_white responsiveness_black
--------- -------- --------- ------------ ---------------------- ----------------------
951765440 2.32495 good VISp 0.14 0.28
951765454 22.6523 good VISp 0.02 0.02
951765460 2.29829 good VISp 0.18 0
951765467 25.8091 good VISp 0.17 0.22
951765485 22.9616 good VISp 0.15 0.39
951765547 2.83687 good VISp 0.39 0
951765552 5.69507 good VISp 0.75 0.81
951765557 6.87888 good VISp 0.14 0.16
951765582 16.7119 good VISp 0.3 0.36
951765594 2.98618 good VISp 0.04 0.21
951765606 4.04201 good VISp 0.27 0.41
951765611 31.0989 good VISp 0.07 0.07
951765623 8.47862 good VISp 0.25 0.05
951765653 7.81739 good VISp 0.17 0.19
951765661 14.579 good VISp 0.08 0.06
951765666 5.01251 good VISp 0.49 0.44
951765669 6.92687 good VISp 0.09 0.25
951765675 18.9142 good VISp 0.33 0.2
951765681 14.8242 good VISp 0.04 0.09
951765686 11.4915 good VISp 0.21 0.4
951765692 2.57025 good VISp 0.03 0.16
951765697 5.22048 good VISp 0.43 0.06
951765716 2.10632 good VISp 0.02 0.23
951765721 8.19066 good VISp 0.23 0.41
951765727 9.74774 good VISp 0.05 0.44
951765732 4.31929 good VISp 0.9 1
951765737 6.79356 good VISp 0.12 0.25
951765769 8.68658 good VISp 0.15 0.14
951765793 4.4846 good VISp 0.02 0.25
951765809 5.36979 good VISp 0.09 0
951765820 5.92437 good VISp 0.03 0.2
951765886 2.35695 good VISp 0.36 0.08
951768133 2.24497 good VISp 0.02 0.28
951768139 6.75623 good VISp 0.03 0.51
951768154 2.82087 good VISp 0.64 0.89
951768183 6.07367 good VISp 0.24 0.41
951768188 5.18849 good VISp 0.33 0
951768222 41.124 good VISp 0.07 0.32
951768247 10.121 good VISp 0.38 0.43
951768278 3.43944 good VISp 0.5 0.66
951768285 4.06867 good VISp 0.91 0.3
951768291 2.77821 good VISp 0.99 0.5
951768298 7.65208 good VISp 0 0.13
951768307 2.32495 good VISp 0.88 0.5
951768318 8.25998 good VISp 0.16 0.72
951768327 3.33812 good VISp 0.57 0.41
951768332 31.4509 good VISp 0.08 0.43
951768345 20.5566 good VISp 0.13 0.36
951768369 9.82773 good VISp 0.17 0.31
951768374 10.9315 good VISp 0.2 0.52
951768390 25.5692 good VISp 0.13 0.36
951768402 6.98553 good VISp 0.15 0.28
951768408 11.6461 good VISp 0 0.27
951768421 13.4538 good VISp 0.09 0.13
951768427 5.65774 good VISp 0.08 0.59
951768434 11.6514 good VISp 0.12 0.07
951768441 25.7291 good VISp 0.07 0.25
951768446 9.42779 good VISp 0.12 0.48
951768451 13.9231 good VISp 0.03 0.04
951768457 5.48177 good VISp 0.18 0.52
951768462 2.36761 good VISp 0.25 0.36
951768473 5.15649 good VISp 0.23 0.12
951768480 8.93187 good VISp 0.33 0.39
951768495 14.9895 good VISp 0.13 0.08
951768500 9.82773 good VISp 0.78 0.89
951768524 2.2183 good VISp 0.13 0.03
951768550 3.96735 good VISp 0.19 0.44
951768557 3.92469 good VISp 0.46 0.81
951768568 13.7737 good VISp 0.03 0.06
951768581 2.61291 good VISp 0.05 0.23
951768586 2.82087 good VISp 0.59 0.52
951768604 3.54076 good VISp 0.13 0.2
951768621 3.41278 good VISp 0.35 0.59
951768627 12.3766 good VISp 0.08 0.22
951768632 5.93503 good VISp 0.16 0.79
951768649 4.22864 good VISp 0.38 0.04
951768673 2.39428 good VISp 0.49 0.07
951768705 7.49744 good VISp 0.2 0.09
951768712 4.48993 good VISp 0.08 0.48
951768723 2.77288 good VISp 0.25 0.21
951768749 2.04767 good VISp 0.94 0.91
951768754 2.76755 good VISp 0.78 1
951768766 11.3208 good VISp 0.01 0.34
951768793 6.27098 good VISp 0.11 0.06
951768815 2.23963 good VISp 0.59 0.76
951768823 5.40712 good VISp 0.03 0.4
951768830 7.58276 good VISp 0.15 0.47
951768835 5.60442 good VISp 0.07 0.27
951768881 4.01534 good VISp 0.5 0.27
951768894 4.2713 good VISp 0.09 0.46
951769295 2.23963 good VISp 0.2 0.45
951769344 2.91152 good VISp 0.68 0.92
Now I can keep the top 15% most responsive units for ongoing analyses.
# Get threshold for top 15% most responsive
thresh_black = np.percentile(units["responsiveness_black"], 85)
thresh_white = np.percentile(units["responsiveness_white"], 85)
# Only keep units that are within the 15% most responsive for either black or white
units = units[(units["responsiveness_black"] > thresh_black) | (units["responsiveness_white"] > thresh_white)]
print(units)
print(f"\nRemaining units: {len(units)}")
Index rate quality brain_area responsiveness_white responsiveness_black
--------- ------- --------- ------------ ---------------------- ----------------------
951765552 5.69507 good VISp 0.75 0.81
951765732 4.31929 good VISp 0.9 1
951768154 2.82087 good VISp 0.64 0.89
951768278 3.43944 good VISp 0.5 0.66
951768285 4.06867 good VISp 0.91 0.3
951768291 2.77821 good VISp 0.99 0.5
951768307 2.32495 good VISp 0.88 0.5
951768318 8.25998 good VISp 0.16 0.72
951768327 3.33812 good VISp 0.57 0.41
951768427 5.65774 good VISp 0.08 0.59
951768500 9.82773 good VISp 0.78 0.89
951768557 3.92469 good VISp 0.46 0.81
951768586 2.82087 good VISp 0.59 0.52
951768621 3.41278 good VISp 0.35 0.59
951768632 5.93503 good VISp 0.16 0.79
951768749 2.04767 good VISp 0.94 0.91
951768754 2.76755 good VISp 0.78 1
951768815 2.23963 good VISp 0.59 0.76
951769344 2.91152 good VISp 0.68 0.92
Remaining units: 19
Revision of stimuli and spiking data#
Now that we have selected the units we will use for our analyses, we can see how these look alongside the stimuli in a raster plot:
Show code cell source
def raster_plot(data, units, n_neurons=len(units), n_flashes=5, n_seconds=13, offset=0.5):
"""
Plot a raster of spiking activity for a subset of neurons during the initial stimulus presentations.
This function visualizes spike times as a raster plot for a selected number of neurons
over a specified time window. The spikes are aligned with stimulus presentations, and
flashes of different types (white or black) are shown as shaded regions in the background.
Parameters
----------
data : nap.TsGroup
A `TsGroup` object which contains all info of all units' spikes without any filtering
units : nap.TsdFrame
A `TsdFrame` object where each column corresponds to the spike train of a neuron. It contains only the filtered neurons after preprocessing
n_neurons : int, optional
Number of neurons to include in the plot. Defaults to the total number of units.
n_flashes : int, optional
Number of white and black flash presentations to show. Defaults to 5.
n_seconds : float, optional
Total duration (in seconds) of the time window to display. Defaults to 13 seconds.
offset : float, optional
Time (in seconds) to start plotting before the first flash. Useful to visualize pre-stimulus activity.
Defaults to 0.5 seconds.
Returns
-------
None
Displays a raster plot using `matplotlib`.
Notes
-----
- The flashes are overlaid using `axvspan`, with white flashes in light gray and black flashes in black.
- Each spike is drawn as a vertical line ('|') at its timestamp.
- Spike times are converted to a single `Tsd` object with unique identifiers for each unit to facilitate plotting.
"""
start = data["flashes_presentations"]["start"].min() - offset
end = start + n_seconds
# Select full spiking activity from units without restriction
units_ = data["units"]
# Select a subset from those - the filtered ones
units = units_[units.index]
# Restrict the spike trains to the selected time window
units = units.restrict(nap.IntervalSet(start, end))
# Convert spike trains to a single Tsd object and label each neuron for plotting
neurons_to_plot = units.to_tsd([i + 1 for i in range(n_neurons)])
fig, ax = plt.subplots(figsize=(17, 4))
ax.plot(neurons_to_plot, "|", markersize=2, mew=2)
# Overlay white flashes
for s, e in zip(flashes_white[:n_flashes].start, flashes_white[:n_flashes].end):
ax.axvspan(s - .50, e + .50, color="red", alpha=0.03, ec="black")
ax.axvspan(s, e, color="silver", alpha=0.4, ec="black")
ax.axvline(s - .50, color = "red")
ax.axvline(e + .50, color = "red")
# Overlay black flashes
for s, e in zip(flashes_black[:n_flashes].start, flashes_black[:n_flashes].end):
ax.axvspan(s - .50, e + .50, color="red", alpha=0.03, ec="black")
ax.axvspan(s, e, color="black", alpha=0.4, ec="black")
ax.axvline(s - .50, color = "red")
ax.axvline(e + .50, color = "red")
ax.set_xlabel("Time (s)")
ax.set_ylabel("Unit")
ax.set_title("Primary Visual Cortex (VISp) units spikes and stimuli")
ax.set_xlim(start, end)
plt.show()
raster_plot(data, units)
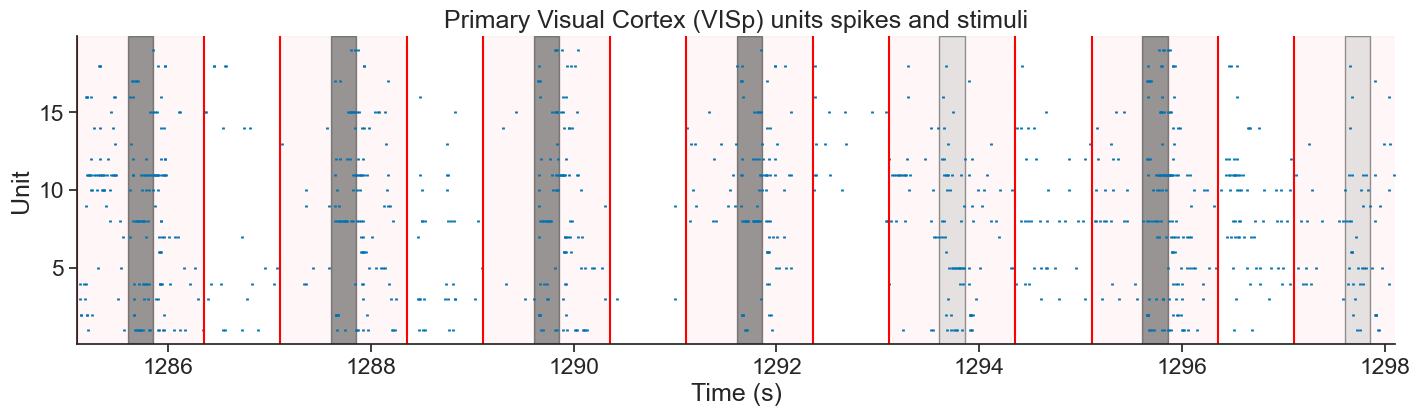
Above we can see a spike raster plot from the selected VISp units displayed alongside the black and white flashes presented to the mice. Each row represents spike times from a different unit. Black and silver bars indicate the presentation of black and white flashes, respectively. The bright red vertical lines mark the windows of interest, 500 ms before stimulus onset and 500 ms after stimulus offset, which are shaded in light red. Spikes occurring within these windows (the shaded red areas) are the ones that will be used for model fitting.
We can also look with each unit’s activity centered around the flashes presentation with a PSTH, as we did before.
# Get the perievent for a subset of the units (most responsive ones)
peri_white = {k: peri_white[k] for k in units.index if k in peri_white}
peri_black = {k: peri_black[k] for k in units.index if k in peri_black}
params_obs = [peri_white,
peri_black]
# Plot PSTH and spike raster plots
plot_raster_psth(peri_white, units, "white", bin_size)
plot_raster_psth(peri_black, units, "black", bin_size)
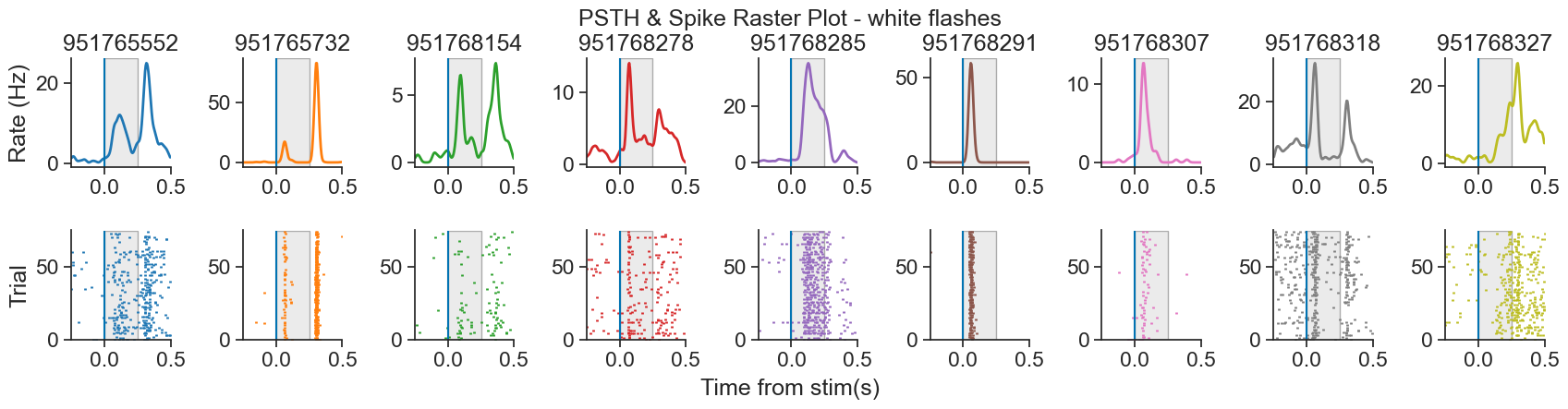
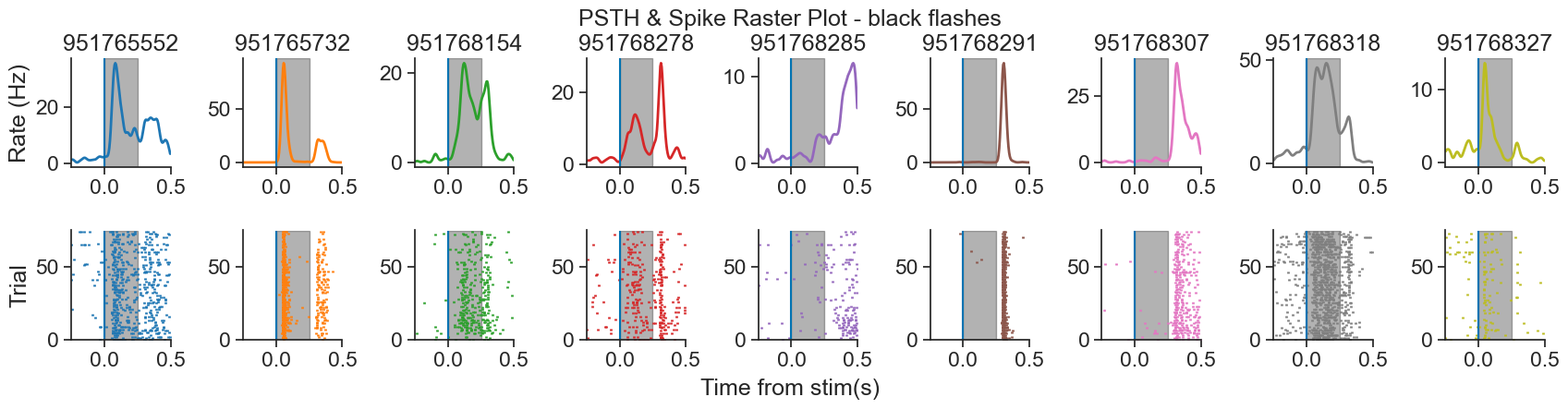
Splitting the dataset in train and test#
We could train the model on the entire dataset. However, if we do so, we wouldn’t have a way to assess whether the model is truly capable of making accurate predictions or if it’s simply overfitting to the data. The simplest way around this is to have a reserved part of the data for testing.
Here, we will split the data in two: 70% will be for training and 30% will be for testing. However, we can’t simply grab the first 70% timeseries - what if we are biasing our sample and there are some neurons that respond only towards the end or the beginning of the recording? For that, we will gather one every three flashes, and those will go to the testing set. The rest, will go to the training set.
How to decide how to split my data?
The optimal way to split your data depends on your specific research question, the structure of your data, and the modeling goals. There’s no single correct approach—splitting strategies can and should be adapted to the context.
For example, you might choose a simple two-way split (training and test), or include a third validation set to tune model parameters before final testing. Some researchers split their data 50/50, while others use more unbalanced ratios depending on dataset size.
In some cases, it may make sense to split based on stimulus properties or experimental design. Suppose you suspect that a mouse’s response to white flashes changes with repeated exposure—e.g., due to habituation. Then, randomly mixing all trials might obscure important patterns. Instead, separating interleaved vs. repeated flash conditions could give you a more meaningful evaluation of model generalization.
# We take one every three flashes (33% of all flashes of test)
flashes_test_white = extended_flashes_white[::3]
flashes_test_black = extended_flashes_black[::3]
Pynapple has a nice function to get all the epochs: set_diff. With it, we can get all of the interval sets which are not in the interval set passed as argument.
# The remaining is separated for training
flashes_train_white = extended_flashes_white.set_diff(flashes_test_white)
flashes_train_black = extended_flashes_black.set_diff(flashes_test_black)
Consider black and white for test and train
using union
# Merge both stimuli types in a single interval set
flashes_test = flashes_test_white.union(flashes_test_black)
flashes_train = flashes_train_white.union(flashes_train_black)
Now that we have our intervals correctly, we can use restrict to get our test and train sets for units
# General spike counts
units_counts = units.count(bin_size, ep = extended_flashes)
# Restrict counts to test and train
units_counts_test = units_counts.restrict(flashes_test)
units_counts_train = units_counts.restrict(flashes_train)
Fitting a GLM#
Preparing the data for NeMoS#
Now that we have a good understanding of our data, and that we have split our dataset in the corresponding test and train subsets, we are almost ready to run our model. However, before we can construct it, we need to get our data in the right format.
When fitting a single neuron, NeMoS requires that the predictors and spike counts it operates on have the following properties:
predictors and spike counts must have the same number of time points.
predictors must be two-dimensional, with shape
(n_time_bins, n_features). So far, we have two features in this tutorial: white and black flashes.spike counts must be one-dimensional, with shape
(n_time_bins,).predictors and spike counts must be jax.numpy arrays, numpy arrays,
TsdorTsdFrame.
When fitting multiple neurons, spike counts must be two-dimensional: (n_time_bins, n_neurons). In that case, spike can be TsGroup objects as well.
First, we can make sure that our predictors and our spike counts have the same number of time bins.
# Create a TsdFrame filled by zeros, for the size of units_counts
predictors = nap.TsdFrame(
t=units_counts.t,
d=np.zeros((len(units_counts), 2)),
columns = ['white', 'black']
)
At the moment, the flashes are in a IntervalSet, we need to grab them and make them time series of stimuli, separated by black and white (because we are interested in how neurons’ responses are modulated by each individual stimulus type separately).
# Check whether there is a flash within a given bin of spikes
# If there is not, put a nan in that index
idx_white = flashes_white.in_interval(units_counts)
idx_black = flashes_black.in_interval(units_counts)
# Replace everything that is not nan with 1 in the corresponding column
predictors.d[~np.isnan(idx_white), 0] = 1
predictors.d[~np.isnan(idx_black), 1] = 1
print(predictors)
Time (s) white black
-------------- ------- -------
1285.103369922 0 0
1285.108369922 0 0
1285.113369922 0 0
1285.118369922 0 0
1285.123369922 0 0
1285.128369922 0 0
1285.133369922 0 0
...
1584.567539922 0 0
1584.572539922 0 0
1584.577539922 0 0
1584.582539922 0 0
1584.587539922 0 0
1584.592539922 0 0
1584.597539922 0 0
dtype: float64, shape: (37500, 2)
predictors and units_counts match in the first dimension because they have the same number of timepoints, as intended. Meanwhile, in the second dimension, predictors is 2 because we have black and white flashes, and counts has 19 because the selected units for this tutorial sums to 19.
print(f"predictors shape: {predictors.shape}")
print(f"\ncount shape: {units_counts.shape}")
Just to make sure that we got the right output, let’s plot our new predictors TsdFrame as lines alongside our first plot.
Show code cell source
def stimuli_plot(predictors, n_flashes = 5, n_seconds = 13, offset = .5):
n_flashes = 5
n_seconds = 13
offset = .5
# Start a little bit earlier than the first flash presentation
start = data["flashes_presentations"]["start"].min() - offset
end = start + n_seconds
fig, ax = plt.subplots(figsize = (17, 4))
# Different coloured flashes
[ax.axvspan(s, e, color = "silver", alpha=.4, ec="black") for s, e in zip(flashes_white[:n_flashes].start, flashes_white[:n_flashes].end)]
[ax.axvspan(s, e, color = "black", alpha=.4, ec="black") for s, e in zip(flashes_black[:n_flashes].start, flashes_black[:n_flashes].end)]
plt.plot(predictors["white"], "o-", color= "silver")
plt.plot(predictors["black"], "o-", color= "black")
plt.xlabel("Time (s)")
plt.ylabel("Absent = 0, Present = 1")
ax.set_title("Presented Stimuli")
plt.xlim(start,end)
# Only use integer values for ticks
ax.yaxis.set_major_locator(MaxNLocator(integer=True))
plt.show()
stimuli_plot(predictors)
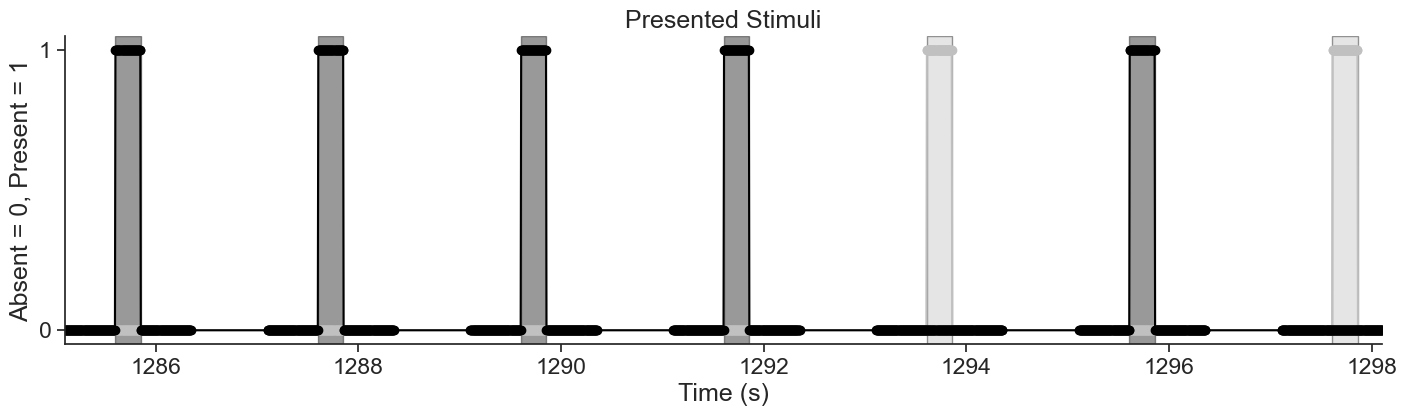
They match perfectly!
As a last preprocessing step, let’s just split predictors in train and test.
predictors_test = predictors.restrict(flashes_test)
predictors_train = predictors.restrict(flashes_train)
Constructing the design matrix using basis functions#
Right now, our predictors consist of the black and white flash values at each time point. However, this setup assumes that the neuron’s spiking behavior is driven only by the instantaneous flash presentation. In reality, neurons integrate information over time — so why not modify our predictors to reflect that?
We can achieve this by including variables that represent the history of exposure to the flashes. For this, we must decide the duration of time that we think is relevant: does the exposure to flashes 10 ms ago matter? What about 100 ms ago? 1s? We should use priori knowledge of our system to determine a initial value.
For this tutorial, we will use the whole duration of the stimuli as relevant history. That is, we will model each unit’s response to 250 ms full-field flashes by capturing how stimulus history over that duration influences spiking. We therefore define a 250 ms stimulus window, aligned with the flash onset, which spans the entire stimulus duration. This window enables the GLM to learn how the neuron’s firing rate evolves throughout the flash. Using a shorter window could omit delayed effects, while a longer window may incorporate unrelated post-stimulus activity.
To construct our stimulus history predictor, we could generate time-lagged copies of the stimulus input (in the form of a Hankel Matrix). Specifically, the value of the first predictor at time \( t \) would correspond to the stimulus at time \( t \), while the second predictor would capture the stimulus at time \( t - 1 \) , and so on, up to a maximum lag corresponding to the length of the stimulus integration window (250 ms in our case).
How do you build a Hankel matrix?
Every row is a shifted copy of the row above!
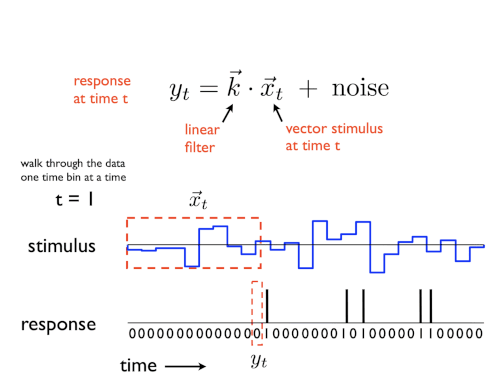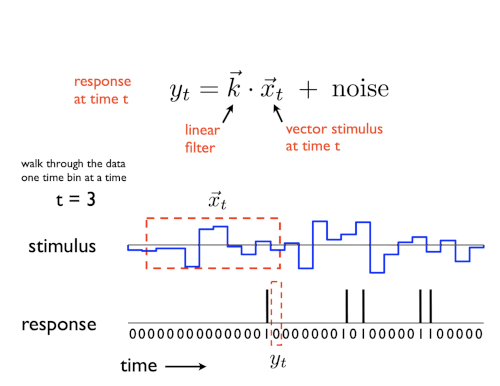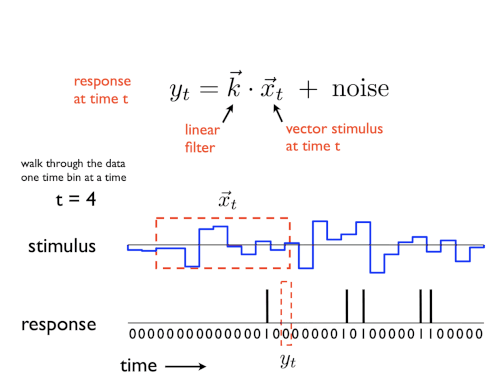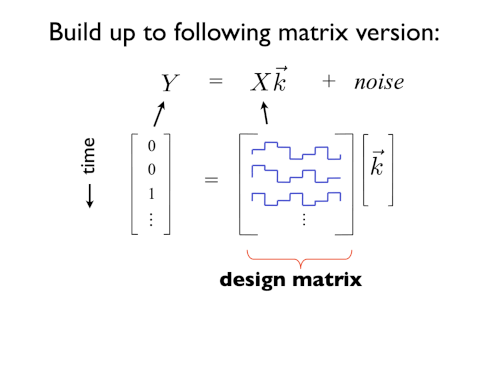
Construction of Hankel Matrix. Modified from Pillow [2018] [3].
For an example on how to build a design matrix using the raw history as a predictor, see this GLM notebook or this NeMoS Fit GLMs for neural coupling tutorial.
However, modeling each time lag with an independent parameter leads to a high-dimensional filter that is prone to overfitting (given that we are using a bin size of 0.005, we would end up with 50 lags = 50 parameters per flash color!) A better idea is to do some dimensionality reduction on these predictors, by parametrizing them using basis functions. This will allow us to capture interesting non-linear effects with a relatively low-dimensional parametrization that preserves convexity.
The way you perform this dimensionality reduction should be carefully considered. Choosing the appropriate type of basis functions, deciding how many to include, and setting their parameters all depend on the specifics of your problem. It’s essential to reflect on which aspects of the stimulus history are worth retaining and how best to represent them. For instance, do you expect sharp transient responses right after stimulus onset? Or are you more interested in slower, sustained effects?
Note
NeMoS has a whole library of basis objects available at nmo.basis. You can explore the different options available there and think carefully about which one best matches your problem and assumptions.
Certain aspects of our units’ response dynamics suggest that applying multiple basis transformations to the stimulus can help better capture the structure that drives the units’ activity. In particular, some neurons exhibit a strong response immediately after flash onset, while others (or the same unit) show an additional peak in activity at flash offset.
Show code cell source
# Plot perievent for a single unit as an example
def plot_peri_single_unit(peri_white, peri_black, unit_id):
fig, ax = plt.subplots(1,2,figsize=(17, 4), sharey=True)
### white
# observed
peri_u = peri_white[unit_id]
peri_u_count = peri_u.count(bin_size)
peri_u_count_conv_mean = np.mean(peri_u_count, 1).smooth(std=0.015)
peri_u_rate_conv = peri_u_count_conv_mean / bin_size
ax[0].plot(peri_u_rate_conv, linewidth=2, color="black")
ax[0].axvspan(0, 0.250, color="silver", alpha=0.3, ec="black")
ax[0].set_xlim(-.25, .5)
ax[0].set_title("White flashes")
#### black
# observed
peri_u = peri_black[unit_id]
peri_u_count = peri_u.count(bin_size)
peri_u_count_conv_mean = np.mean(peri_u_count, 1).smooth(std=0.015)
peri_u_rate_conv = peri_u_count_conv_mean / bin_size
ax[1].plot(peri_u_rate_conv, linewidth=2, color="black", label = "observed")
ax[1].axvspan(0, 0.250, color="black", alpha=0.3, ec="black")
ax[1].set_xlim(-.25, .5)
ax[1].set_title("Black flashes")
ax[0].set_ylabel("Rate (Hz)")
fig.text(0.5, -.05, 'Time from stim(s)', ha='center')
fig.text(0.5, .95, f'PSTH unit {unit_id}', ha='center')
plt.show()
# Choose an example unit
unit_id = 951768318
plot_peri_single_unit(peri_white, peri_black, unit_id)
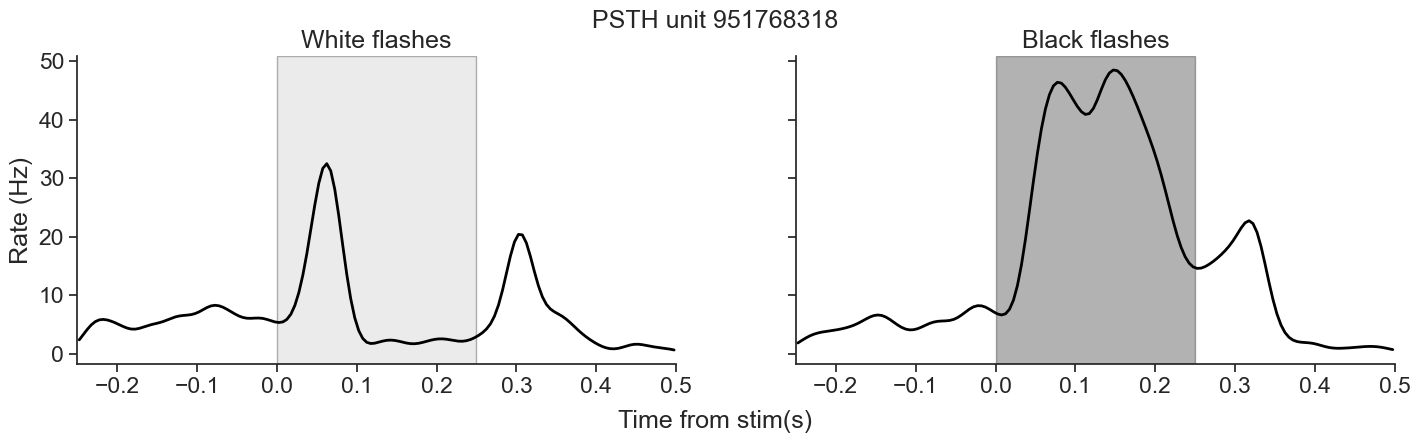
These distinct temporal features motivate us to model the onset and offset components separately, using tailored basis functions for each. Considering that, we will apply three distinct transformations to our predictors, each targeting a specific portion or feature of the stimulus:
Flash onset (beginning): We will convolve the early phase of the flash presentation with a basis function. This allows for fine temporal resolution immediately after stimulus onset, where rapid neural responses are often expected.
Flash offset (end): We will convolve the later phase of the flash (around its end) with a different basis function. This emphasizes activity changes around stimulus termination.
Full flash duration (smoothing): We will convolve the entire flash period with a third basis function, serving as a smoother to capture more sustained or slowly varying effects across the full stimulus window.
First, we will transform our predictors to get flash onset and offset. We should do this for train
white_train_on = nap.Tsd(
t=predictors_train.t,
d=np.hstack((0,np.diff(predictors_train["white"])==1)),
time_support = units_counts_train.time_support
)
white_train_off = nap.Tsd(
t=predictors_train.t,
d=np.hstack((0,np.diff(predictors_train["white"])==-1)),
time_support = units_counts_train.time_support
)
# Black train
black_train_on = nap.Tsd(
t=predictors_train.t,
d=np.hstack((0,np.diff(predictors_train["black"])==1)),
time_support = units_counts_train.time_support
)
black_train_off = nap.Tsd(
t=predictors_train.t,
d=np.hstack((0,np.diff(predictors_train["black"])==-1)),
time_support = units_counts_train.time_support
)
and test set.
# White test
white_test_on = nap.Tsd(
t=predictors_test.t,
d=np.hstack((0,np.diff(predictors_test["white"])==1)),
time_support=units_counts_test.time_support
)
white_test_off = nap.Tsd(
t=predictors_test.t,
d=np.hstack((0,np.diff(predictors_test["white"])==-1)),
time_support=units_counts_test.time_support
)
# Black test
black_test_on = nap.Tsd(
t=predictors_test.t,
d=np.hstack((0,np.diff(predictors_test["black"])==1)),
time_support=units_counts_test.time_support
)
black_test_off = nap.Tsd(
t=predictors_test.t,
d=np.hstack((0,np.diff(predictors_test["black"])==-1)),
time_support=units_counts_test.time_support
)
What are np.diff and np.hstack doing?
np.diff is a NumPy function that computes the difference between consecutive elements in an array.
Our stimulus predictors are binary: they take the value 0 when no flash is present, and 1 during the flash. For example, a typical pattern might look like:
[0, 0, 0, 0, 1, 1, 1, 0, 0]
Calling np.diff on this array will compute:
[0, 0, 0, 1, 0, 0, -1, 0]
This result highlights transitions:
A value of 1 indicates the start of a flash (0 → 1),
A value of -1 indicates the end of a flash (1 → 0),
All other values represent no change.
However, because np.diff returns an array that is one element shorter than the original, we prepend a 0 using np.hstack to align it with the original timestamps.
We now have our predictors, it’s time to choose which basis functions are the most suitable for our ends.
For history-type inputs like we’re discussing, the raised cosine log-stretched basis first described in Pillow et al. [2005] [4] is a good fit. This basis set has the nice property that their precision drops linearly with distance from event, which makes sense for many history-related inputs in neuroscience: whether an input happened 1 or 5 ms ago matters a lot, whereas whether an input happened 51 or 55 ms ago is less important. We will apply this basis function to the beginning of the flash.
Show code cell source
# Duration of stimuli
stimulus_history_duration = 0.25
# Window length in bin size units
window_len = int(stimulus_history_duration / bin_size)
basis_example = nmo.basis.RaisedCosineLogConv(
n_basis_funcs = 5,
window_size = window_len,
)
sample_points, basis_values = basis_example.evaluate_on_grid(100)
fig, ax = plt.subplots(figsize=(5, 3))
ax.plot(sample_points, basis_values)
ax.set_title("Raised cosine log-stretched basis")
ax.set_ylabel("Amplitude")
ax.set_xlabel("Time Lag")
plt.show()
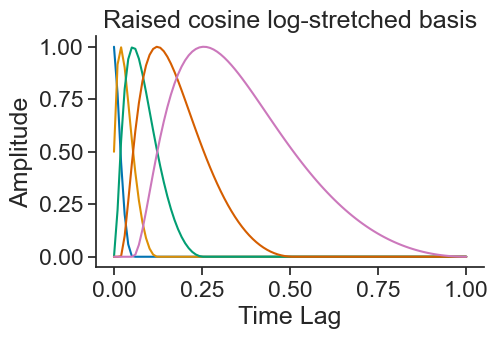
Another very useful transformation we can apply to our predictors is that of the raised cosine linearly spaced basis, in which the domain is uniformly covered. This is an interesting basis because it is symmetric. We will apply this to the end of the flash.
Show code cell source
# Duration of stimuli
stimulus_history_duration = 0.25
# Window length in bin size units
window_len = int(stimulus_history_duration / bin_size)
basis_example = nmo.basis.RaisedCosineLinearConv(
n_basis_funcs = 5,
window_size = window_len,
)
sample_points, basis_values = basis_example.evaluate_on_grid(100)
fig, ax = plt.subplots(figsize=(5, 3))
ax.plot(sample_points, basis_values)
ax.set_title("Raised cosine linear basis")
ax.set_ylabel("Amplitude")
ax.set_xlabel("Time Lag")
plt.show()
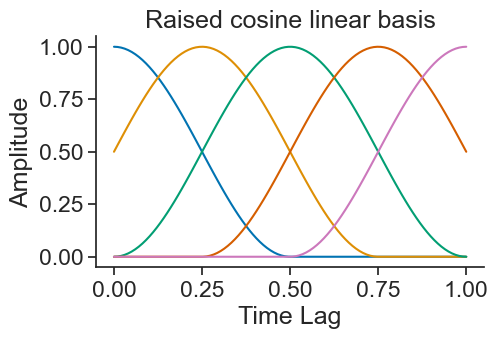
To see how these look convolved with the stimuli, let’s create our basis objects!
When we instantiate a basis object, the only arguments we must specify is the number of functions we want and the mode of operation of the basis:
Number of functions: with more basis functions, we’ll be able to represent the effect of the corresponding input with the higher precision, at the cost of adding additional parameters.
Mode of operation: either
Convfor convolutional orEvalfor evaluation form of the basis. This is determined by the type of feature we aim to represent. This is not a parameter; instead, the choice of basis will includeConvorEvalin the name.
When should I use the convolutional or evaluation form of the basis?
Evaluation bases transform the input through the non-linear function defined by the basis. This can be used to represent features such as spatial location and head direction.
Convolution bases apply a convolution of the input data to the bank of filters defined by the basis, and is particularly useful when analyzing data with inherent temporal dependencies, such as spike history or the history of flash exposure in this example. In convolution mode, we must additionally specify the
window_size(the length of the filters in bins).
Since we are using Convolution bases, we need to specify the window_size. In this tutorial, we will use 250 ms.
# Duration of stimuli
stimulus_history_duration = 0.250
# Window length in bin size units
window_len = int(stimulus_history_duration / bin_size)
Now we can initialize our basis objects. As mentioned, for each flash type (white and black), we will create three separate basis objects: one for the onset of the flash, one for the offset, and one that spans the entire duration of the flash. In this tutorial, each basis object will have 5 basis functions.
How many functions should I use for each basis object?
When conducting your own analysis, you should carefully consider what number of basis functions is optimal for your specific dataset and scientific question. Too few may poorly predict the dynamics; too many may lead to overfitting or unnecessary complexity. You can conduct cross validation to find the optimal number of basis functions. For more information on how to tune your bases, you can refer to NeMoS notebook on conducting cross validation for bases.
# Initialize basis objects
# White
# Raised Cosine Log Stretched basis for "On"
basis_white_on = nmo.basis.RaisedCosineLogConv(
n_basis_funcs = 5,
window_size = window_len,
label = "white_on"
)
# Raised Cosine Linear basis for "Off"
basis_white_off = nmo.basis.RaisedCosineLinearConv(
n_basis_funcs = 5,
window_size = window_len,
label = "white_off",
conv_kwargs = {"predictor_causality":"acausal"}
)
# Raised Cosine Log Stretched basis for smoothing throughout stimuli presentaiton
basis_white_stim= nmo.basis.RaisedCosineLogConv(
n_basis_funcs = 5,
window_size = window_len,
label = "white_stim"
)
# Black
# Raised Cosine Log Stretched basis for "On"
basis_black_on = nmo.basis.RaisedCosineLogConv(
n_basis_funcs = 5,
window_size = window_len,
label = "black_on"
)
# Raised Cosine Linear basis for "Off"
basis_black_off = nmo.basis.RaisedCosineLinearConv(
n_basis_funcs = 5,
window_size = window_len,
label = "black_off",
conv_kwargs = {"predictor_causality":"acausal"}
)
# Raised Cosine Log Stretched basis for smoothing throughout stimuli presentaiton
basis_black_stim = nmo.basis.RaisedCosineLogConv(
n_basis_funcs = 5,
window_size = window_len,
label = "black_stim"
)
What is the predictor_causality parameter doing in the initialization of the RaisedCosineLinearConv basis?
This manages the causality of the predictor: "causal" is the default setting, and it means that the convolution will occur with respect to the input. Conversely "acausal", the one we are using now for the raised cosine linear basis, applies the convolution to both sides of the stimulus equally. For more information, please refer to NeMoS notebook on causal, anti-causal and acausal filters
Using the compute_features function, NeMoS convolves our input features (predictors) with the basis object to compress them. Let’s see how that looks!
Show code cell source
def plot_basis_feature_summary(
basis_object,
predictors,
interval,
label,
window_len,
title
):
"""
Plot summary of basis functions and convolved features for a given input.
Parameters
----------
basis_object : object
A basis object implementing `compute_features()` and `evaluate_on_grid()`.
predictors : Tsd or TsdFrame
Time series of stimulus predictors to convolve.
interval : nap.IntervalSet
Interval to restrict the predictors and features to.
label : str
Label for the raw stimulus trace (e.g. "Flash").
window_len : float
Duration of the window used to scale the basis time axis.
title : str
Title to display above the figure.
"""
# Restrict raw stimulus first
restricted_input = predictors.restrict(interval)
# Compute features from numeric values (NeMoS expects array-like with astype)
features = basis_object.compute_features(np.asarray(restricted_input.d, dtype=float))
# Create time axis for basis
time, basis = basis_object.evaluate_on_grid(basis_object.window_size)
time *= window_len
# Initialize plot
fig, axes = plt.subplots(2, 3, sharey="row", figsize=(12, 2.5), tight_layout=True)
# Plot raw predictors
for ax in axes[1, :]:
ax.plot(restricted_input, "k--", label="true")
ax.set_xlabel("Time (s)")
# Plot first basis function and its feature
axes[0, 0].plot(time, basis, alpha=0.1)
axes[0, 0].plot(time, basis[:, 0], "C0", alpha=1)
axes[0, 0].set_xticks([])
axes[0, 0].set_ylabel("Amp.")
axes[0, 0].set_yticks([])
axes[0, 0].set_title("Feature 1")
axes[1, 0].plot(features[:, 0], label="conv.")
axes[1, 0].set_ylabel(label)
axes[1, 0].set_yticks([])
# Plot last basis function and its feature
last_idx = basis.shape[1] - 1
color = f"C{last_idx}"
axes[0, 1].plot(time, basis[:, last_idx], color, alpha=1)
axes[0, 1].plot(time, basis, alpha=0.1)
axes[0, 1].set_xticks([])
axes[0, 1].set_title(f"Feature {basis.shape[1]}")
axes[1, 1].plot(features[:, -1], color)
# Plot all basis functions and features
axes[0, 2].plot(time, basis)
axes[0, 2].set_xticks([])
axes[0, 2].set_title("All features")
axes[1, 2].plot(features)
fig.text(0.5, 1.00, title, ha='center')
plt.show()
interval = flashes_train_white[0]
plot_basis_feature_summary(
basis_white_on,
white_train_on,
interval,
label="Flash",
window_len=window_len,
title="Flashes On - Raised Cosine Log-Stretched Conv"
)
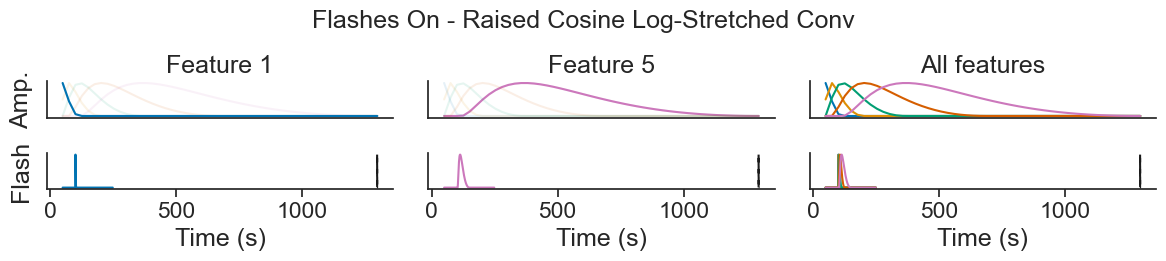
On the top row, we can see the basis function, same as in the plot “Raised cosine log-stretched basis” above. On the bottom row, we are showing the beginning of one flash presentation, as a dashed line, and corresponding features over a small window of time. These features are the result of a convolution between the basis function on the top row with the black dashed line showed below. The basis functions get progressively wider and delayed from the flash onset, so we can think of the features as weighted averages that get progressively later and smoother.
In the leftmost plot, we can see that the first feature almost perfectly tracks the input. Looking at the basis function above, that makes sense: this function’s max is at 0 and quickly decays. In the middle plot, we can see that the last feature has a fairly long lag compared to the flash beginning, and is a lot smoother. Looking at the rightmost plot, we can see that the other features vary between these two extremes, getting smoother and more delayed.
Now let’s see how our convolved features look for the basis for a instance of full flash duration:
plot_basis_feature_summary(
basis_white_stim,
predictors_train["white"],
interval,
label="Flash",
window_len=window_len,
title="Flash Presentation - Raised Cosine Log-Stretched Conv"
)
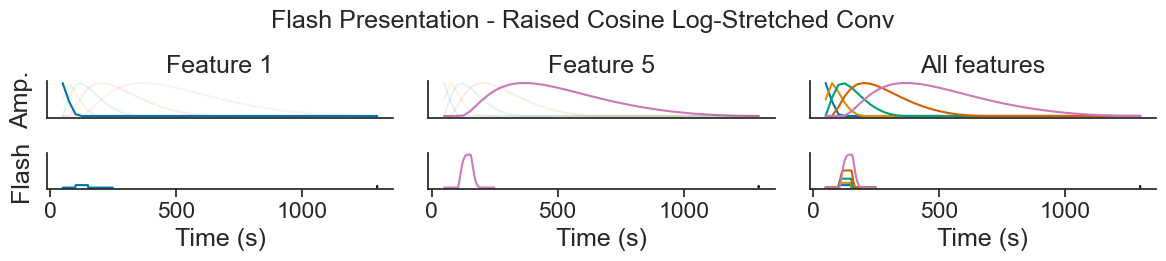
This is very similar to the Flashes On convolution, just a bit wider, as the duration of the flash is longer than a single instance of initiation of flash.
Finally, let’s see how our Raised Cosine Linear Conv basis is transforming our Flashes Off predictor.
plot_basis_feature_summary(
basis_white_off,
white_train_off,
interval,
label="Flash",
window_len=window_len,
title="Flashes Off - Raised Cosine Linear Conv"
)
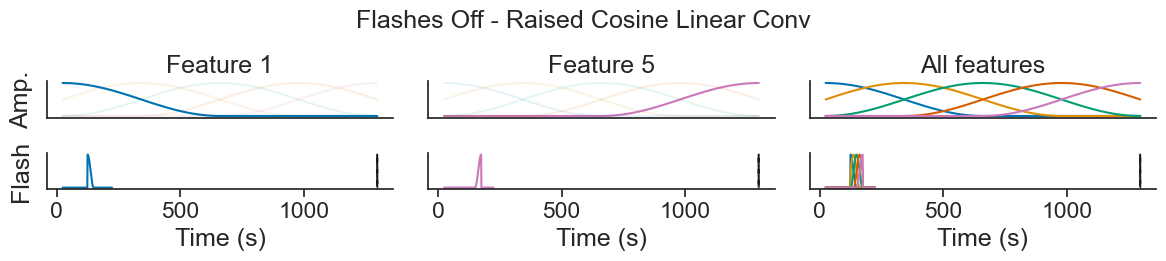
This basis might look a bit different, and that’s because we’re using the "acausal"setting for the "predictor_causality" option. In this mode, the center of the convolution is aligned with the end of the flash, rather than strictly following the stimulus forward in time.
This acausal alignment allows the model to capture changes in firing rate that occur both just before and after the flash ends. This is particularly useful for smoothing transitions between basis-driven components: it helps avoid abrupt or artificial jumps in the predicted firing rate at stimulus offset. Instead, we can interpolate more smoothly across time, producing more interpretable predictions.
These are the elements of our feature matrix: representations of not just the instantaneous presentation of a flash, but also of its history. Let’s see what this looks like when we go to fit the model!
In our case, we want our basis to be composed by both black and white flashes features. For that, we can build an additive basis. This will concatenate our already declared basis objects.
# Define additive basis object
additive_basis = (
basis_white_on +
basis_white_off +
basis_white_stim +
basis_black_on +
basis_black_off +
basis_black_stim
)
We can convolve our predictors with each basis within our additive basis by calling compute_features.
# Convolve basis with inputs - train set
X_train = additive_basis.compute_features(
np.asarray(white_train_on.d, dtype=float),
np.asarray(white_train_off.d, dtype=float),
np.asarray(predictors_train["white"], dtype=float),
np.asarray(black_train_on.d, dtype=float),
np.asarray(black_train_off.d, dtype=float),
np.asarray(predictors_train["black"], dtype=float)
)
# Convolve basis with inputs - test set
X_test = additive_basis.compute_features(
np.asarray(white_test_on.d, dtype=float),
np.asarray(white_test_off.d, dtype=float),
np.asarray(predictors_test["white"], dtype=float),
np.asarray(black_test_on.d, dtype=float),
np.asarray(black_test_off.d, dtype=float),
np.asarray(predictors_test["black"], dtype=float)
)
More resources on basis functions
NeMoS fit head-direction population tutorial: For a step by step explanation of how to build the design matrix first as a result of convolving the features with the identity matrix, and then by using basis functions, alongside nice visualizations.
Flatiron Institute Introduction to GLMs tutorial: For a detailed explanation, step by step, on how predictors look with and without basis functions, with nice visualizations as well.
NeMoS notebook on composition of basis functions: For a detailed explanation of the different operations that can be carried out using basis functions in 2 and more dimensions.
Bishop, 2009: Section 3.1 for a formal description of what basis functions are and some examples of them.
NeMoS notebook on conducting cross validation for bases: For a detailed explanation of how to combine NeMos objects within a scikit-learn pipeline to select the number of bases and bases type using cross validation.
Initialize and fit a GLM: single unit#
Now we are finally ready to start our model!
First, we need to define our GLM model object. To initialize our model, we need to specify the solver_name, the regularizer, the regularizer_strength and the observation_model. All of these are optional.
solver_name: this string specifies the solver algorithm. The default behavior depends on the regularizer, as each regularization scheme is only compatible with a subset of possible solvers.regularizer: this string or object specifies the regularization scheme. Regularization modifies the objective function to reflect your prior beliefs about the parameters, such as sparsity. Regularization becomes more important as the number of input features, and thus model parameters, grows. NeMoS’s solvers can be found within thenemos.regularizermodule.observation_model: this object links the firing rate and the observed data (in this case spikes), describing the distribution of neural activity (and thus changing the log-likelihood). For spiking data, we use the Poisson observation model.
For this tutorial, we’ll use a LBFGS solver_name with Ridge regularizer, and a regularizer_strength of 7.745e-06
Why LBFGS?
LBFGS is a quasi-Netwon method, that is, it uses the first derivative (the gradient) and approximates the second derivative (the Hessian) in order to solve the problem. This means that LBFGS tends to find a solution faster and is often less sensitive to step-size. Try other solvers to see how they behave!
What is regularization?
When fitting models, it is generally recommended to use regularization, a technique that adds a constraint or penalty to the model’s cost function. Regularization works by discouraging the coefficients from reaching large values.
Penalizing large coefficients is beneficial because it helps prevent overfitting, a phenomenon in which the model fits the training data too closely, capturing noise instead of the underlying pattern. Large coefficients often indicate a model that is too complex or sensitive to small fluctuations in the data. By keeping coefficients smaller and more stable, regularization promotes simpler models that generalize better to unseen data, improving predictive performance and robustness.
In this tutorial, we will use Ridge regularization (or L2 regularization). In this type of regularization, the penalty term added to the loss function is:
where \(\lambda\) is the regularization strength, \(N\) is the number of samples and \(\theta_j\) are the model coefficients, stored in model.coef_.
Please refer to NeMoS documentation for more details on how this was implemented.
regularizer_strength = 7.745e-06
# Initialize model object of a single unit
model = nmo.glm.GLM(
regularizer = "Ridge",
regularizer_strength = regularizer_strength,
solver_name="LBFGS",
)
Where did the regularizer_strength value come from?
We conducted cross validation to obtain the regularization strength:
from sklearn.model_selection import GridSearchCV
# Initialize model object
model = nmo.glm.GLM(
regularizer = "Ridge",
regularizer_strength = 0.01,
solver_name="LBFGS",
#solver_kwargs=dict(tol=10**-12)
)
# Create parameter grid
param_grid = {
"regularizer_strength" :
np.geomspace(10**-9, 10, 10)
}
# Instantiate the grid search object
grid_search = GridSearchCV(
model,param_grid,
cv=5
)
# Run grid search
grid_search.fit(X_train, u_counts_train)
# Print optimal parameter
print(grid_search.best_estimator_.regularizer_strength)
>>> 7.742636826811277e-06
In this tutorial, for conciseness, we will use the regularizer strength obtained for this single neuron across the entire population. However, please note that when running your own analysis, it is necessary to find the optimal regularizer strength for each neuron individually, as there is no guarantee that the optimal solution for one neuron will also be optimal for another.
First let’s choose an example unit to fit.
# Choose an example unit
unit_id = 951768318
# Get counts for train and test for said unit
u_counts_train = units_counts_train.loc[unit_id]
u_counts_test = units_counts_test.loc[unit_id]
NeMoS models are intended to be used like scikit-learn estimators. In these, a model instance is initialized with hyperparameters (like regularization strength, solver, etc), and then we can call the fit() function to fit the model to data. Since we have already created our model and have our data, we can go ahead and call fit().
model.fit(X_train, u_counts_train)
GLM(
observation_model=PoissonObservations(),
inverse_link_function=exp,
regularizer=Ridge(),
regularizer_strength=7.745e-06,
solver_name='LBFGS'
)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| observation_model | PoissonObservations() | |
| inverse_link_function | <function exp...001D8FA7C84C0> | |
| regularizer | Ridge() | |
| regularizer_strength | 7.745e-06 | |
| solver_name | 'LBFGS' | |
| solver_kwargs | {} |
Now that we have fit our data, we can retrieve the resulting parameters. Similar to scikit-learn , these are stored as the coef_.and intercept_ attributes:
print(f"firing_rate(t) = exp({model.coef_} * flash(t) + {model.intercept_})")
firing_rate(t) = exp([ 0.6043559 0.44007504 -2.1450105 2.0849879 3.6571403 1.8352346
2.5368817 3.1204095 3.9219391 0.09251922 -1.0855266 2.3020031
-1.8775219 0.6012459 -0.3855391 1.2680908 -0.07725894 -0.26846427
0.25450337 3.0106094 -0.23731844 2.050686 -0.6714147 1.3555073
-0.80394244 -0.44227383 0.33053422 -0.12981808 -0.07138676 0.07499503] * flash(t) + [-3.8936982])
Note
Note that model.coef_ has shape (n_features, ), while model.intercept_ has shape (n_neurons):
print(model.coef_.shape)
>>> (30,)
print(model.intercept_.shape)
>>> (1,)
Assess GLM performance: predict and PSTH#
Although it is helpful to examine the model parameters, they don’t tell us much about how well the model is performing. So how can we assess its quality?
One way is to use the model to predict firing rates and compare those predictions to the smoothed spike train. By calling predict, we obtain the model’s predicted firing rate for the input data — that is, the output of the nonlinearity.
# Use predict to obtain the firing rates
pred_unit = model.predict(X_test)
# Convert units from spikes/bin to spikes/sec and wrap as a Pynapple time series
pred_unit = nap.Tsd(
t=u_counts_test.t,
d=np.asarray(pred_unit, dtype=float) / bin_size,
time_support=u_counts_test.time_support,
)
print(pred_unit)
Time (s)
-------------- ---
1285.103369922 nan
1285.108369922 nan
1285.113369922 nan
1285.118369922 nan
1285.123369922 nan
1285.128369922 nan
1285.133369922 nan
...
1576.560859922 nan
1576.565859922 nan
1576.570859922 nan
1576.575859922 nan
1576.580859922 nan
1576.585859922 nan
1576.590859922 nan
dtype: float64, shape: (12500,)
Why is our time series full of NaN values!?
IT IS NOT! We have NaN values at the beginning and end of each flash presentation. This is due to the convolution window used when applying the basis functions. In our case, the model uses a 250 ms temporal window, meaning that at any given time point, the model looks back 250 ms into the stimulus history.
As a result, during the first 250 ms of each trial, the convolution cannot be fully computed — the model lacks sufficient preceding data to construct the input to the linear filter. This leads to NaN values in the predicted firing rate during this initial period.
Given our bin size of 5 ms, 250 ms corresponds to 50 time bins. Thus, we expect the first 50 time points of the prediction to contain NaNs. After that, the model has enough history to compute valid predictions.
For example, if we inspect the predictions starting at timepoint 50, we no longer see NaN values at the beginning:
print(pred_unit[50:])
>>> Time (s)
-------------- ---------
1285.353369922 3.85464
1285.358369922 3.85464
1285.363369922 3.85464
1285.368369922 3.85464
1285.373369922 3.85464
1285.378369922 3.85464
1285.383369922 3.85464
...
1576.560859922 nan
1576.565859922 nan
1576.570859922 nan
1576.575859922 nan
1576.580859922 nan
1576.585859922 nan
1576.590859922 nan
dtype: float32, shape: (12450,)
By contrast, timepoint 49 still includes a NaN:
print(pred_unit[49:])
>>> Time (s)
-------------- ---------
1285.348369922 nan
1285.353369922 3.85464
1285.358369922 3.85464
1285.363369922 3.85464
1285.368369922 3.85464
1285.373369922 3.85464
1285.378369922 3.85464
...
1576.560859922 nan
1576.565859922 nan
1576.570859922 nan
1576.575859922 nan
1576.580859922 nan
1576.585859922 nan
1576.590859922 nan
dtype: float32, shape: (12451,)
Similarly, we find NaNs at the end of the convolution - specifically in the last 25 bins because the basis for Flashes Off is acausal. Given our 250 ms window, an acausalconvolution means that the convolution is centered in the event (in our case, flash offset), and it requires 125 ms (or 25 bins!) to each side of every timepoint to be computed. When there are 125 ms left to go (or less), the basis does not have enough timepoints to conduct the convolution, and this results in NaN values.
So, the NaNs are not an error — they’re simply a byproduct of the convolution requiring a full 250 ms or 125 ms history before producing an output.
Now, we can use Pynapple function compute_perievent_continuous to re-center the timestamps of the predicted rates around the stimulus presentations, in a similar manner than at the beginning of the tutorial. In contrast to compute_perievent, compute_perievent_continuous allows us to center a continuous time series.
We re-center the timestamps in the same way as we did at the beginning of the tutorial.
# Re-center timestamps around white stimuli
# +50 because we subtracted .50 at beginning of stimulus presentation
peri_white_pred_unit = nap.compute_perievent_continuous(
timeseries = pred_unit,
tref = nap.Ts(flashes_test_white.start+.50),
minmax=window_size
)
# Re-center timestamps for black stimuli
# +50 because we subtracted .50 at beginning of stimulus presentation
peri_black_pred_unit = nap.compute_perievent_continuous(
timeseries = pred_unit,
tref = nap.Ts(flashes_test_black.start+.50),
minmax=window_size
)
# Print centered spikes
print(peri_white_pred_unit)
Time (s) 0 1 2 3 4 ...
---------- ------- ------- ------- ------- ------- -----
-0.25 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.245 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.24 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.235 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.23 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.225 4.07397 4.07397 4.07397 4.07397 4.07397 ...
-0.22 4.07397 4.07397 4.07397 4.07397 4.07397 ...
... ...
0.47 3.98447 3.98447 4.02044 3.98447 3.98447 ...
0.475 4.02044 4.02044 4.04512 4.02044 4.02044 ...
0.48 4.04512 4.04512 4.06069 4.04512 4.04512 ...
0.485 4.06069 4.06069 4.0693 4.06069 4.06069 ...
0.49 4.0693 4.0693 4.07305 4.0693 4.0693 ...
0.495 4.07305 4.07305 4.07397 4.07305 4.07305 ...
0.5 4.07397 4.07397 4.07397 4.07397 4.07397 ...
dtype: float64, shape: (151, 25)
The resulting object is a Pynapple TsdFrame of shape (n_time_bins,n_trials) (we are defining one trial as one presentation of stimuli).
With that, we can plot the PSTH of both the average firing rate of this unit and the average predicted rate.
Show code cell source
def plot_peri_predict(
peri_white_pred_unit,
peri_black_pred_unit,
peri_white,
peri_black,
unit_id = unit_id
):
fig, ax = plt.subplots(1,2,figsize=(17, 4), sharey=True)
### white
# predicted
ax[0].plot(np.mean(peri_white_pred_unit,axis=1), linewidth=1.5, color="red", label = "predicted")
peri_u = peri_white[unit_id]
peri_u_count = peri_u.count(bin_size)
peri_u_count_conv_mean = np.mean(peri_u_count, 1).smooth(std=0.015)
peri_u_rate_conv = peri_u_count_conv_mean / bin_size
# observed
ax[0].plot(peri_u_rate_conv, linewidth=2, color="black")
ax[0].axvline(0.0)
ax[0].axvspan(0, 0.250, color="silver", alpha=0.3, ec="black")
ax[0].set_xlim(-.25, .5)
ax[0].set_title("White flashes")
#### black
# predicted
ax[1].plot(np.mean(peri_black_pred_unit,axis=1), linewidth=1.5, color="red")
peri_u = peri_black[unit_id]
peri_u_count = peri_u.count(bin_size)
peri_u_count_conv_mean = np.mean(peri_u_count, 1).smooth(std=0.015)
peri_u_rate_conv = peri_u_count_conv_mean / bin_size
# observed
ax[1].plot(peri_u_rate_conv, linewidth=2, color="black", label = "observed")
ax[1].axvline(0.0)
ax[1].axvspan(0, 0.250, color="black", alpha=0.3, ec="black")
ax[1].set_xlim(-.25, .5)
ax[1].set_title("Black flashes")
ax[0].set_ylabel("Rate (Hz)")
fig.text(0.5, -.05, 'Time from stim(s)', ha='center')
fig.text(0.5, .95, f'PSTH unit {unit_id}', ha='center')
fig.legend()
plt.show()
plot_peri_predict(peri_white_pred_unit,
peri_black_pred_unit,
peri_white,
peri_black
)
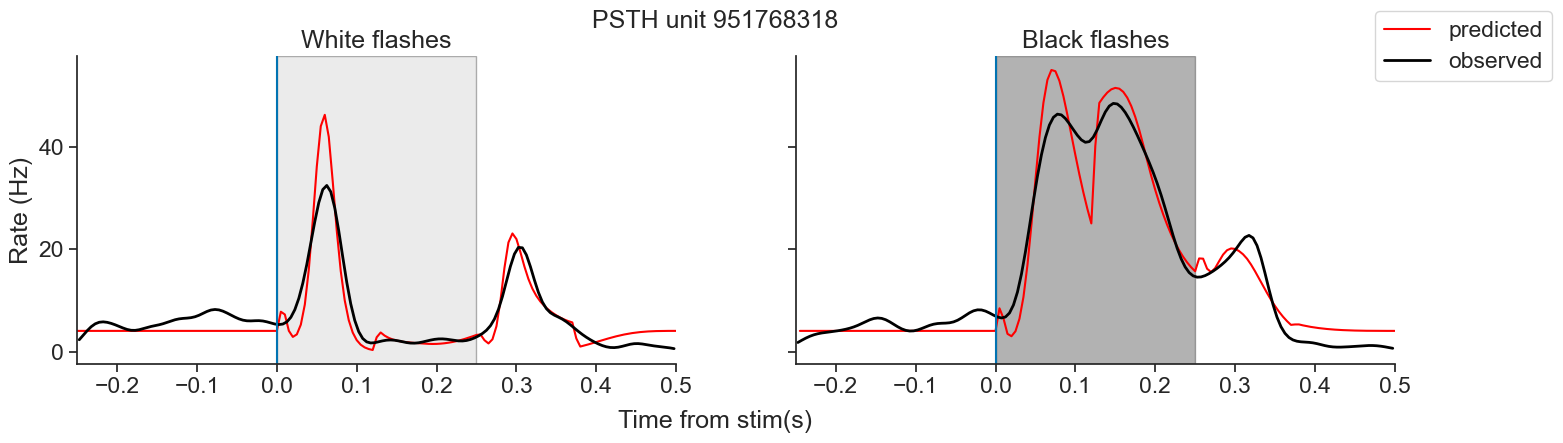
Now, we can move to fit all neurons!
Initialize and fit a GLM: PopulationGLM#
NeMoS has a separate PopulationGLM object for fitting a population of neurons. This is equivalent to fitting each individually in a loop, but faster. It operates very similarly to the GLM object we used a moment ago.
The first step is initializing the model, as with the GLM object.
model_stimuli = nmo.glm.PopulationGLM(
regularizer = "Ridge",
regularizer_strength = regularizer_strength,
solver_name="LBFGS"
)
Our input for the PopulationGLM can be the same basis object we used for fitting a single unit. Since we now want to fit all neurons, the counts for our model will be units_counts_train. With that, we call model_stimuli.fit() to fit our model.
model_stimuli.fit(
X_train,
units_counts_train
)
PopulationGLM(
observation_model=PoissonObservations(),
inverse_link_function=exp,
regularizer=Ridge(),
regularizer_strength=7.745e-06,
solver_name='LBFGS'
)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| observation_model | PoissonObservations() | |
| inverse_link_function | <function exp...001D8FA7C84C0> | |
| regularizer | Ridge() | |
| regularizer_strength | 7.745e-06 | |
| solver_name | 'LBFGS' | |
| solver_kwargs | {} | |
| feature_mask | None |
Same as before, our coefficients live in the coef_ attribute, while our intercept is stored in the intercept_ attribute.
However, since here we have fitted all units, the shape of our coef_ output will be (n_coefficients, n_units). Similarly, the shape of our intercept_ output will be (n_units,) because there is one intercept per unit.
print(model_stimuli.coef_.shape)
print(model_stimuli.intercept_.shape)
(30, 19)
(19,)
Assess PopulationGLM performance: PSTH#
To evaluate how well our PopulationGLM model captures the neural responses, we can visualize the activity of individual units using a PSTH.
For that, we first use the predict function.
# Predict spikes rate of all neurons in the population
predicted = model_stimuli.predict(X_test)
# Convert units from spikes/bin to spikes/sec
predicted = predicted/ bin_size
predicted = nap.TsdFrame(
t=units_counts_test.t,
d=np.asarray(predicted, dtype=float),
time_support=units_counts_test.time_support
)
Then, we use Pynapple function compute_perievent_continuous to re-center the timestamps of the observed and predicted rates around the stimulus presentations.
# Re-center timestamps for test set
peri_white_test = nap.compute_perievent_continuous(
timeseries = units.restrict(flashes_test).count(bin_size),
tref = nap.Ts(flashes_test_white.start+.50),
minmax = (window_size)
)
# Re-center timestampsfor test set
peri_black_test = nap.compute_perievent_continuous(
timeseries = units.restrict(flashes_test).count(bin_size),
tref = nap.Ts(flashes_test_black.start+.50),
minmax = (window_size)
)
# Re-center timestamps for predicted
peri_white_pred = nap.compute_perievent_continuous(
timeseries = predicted,
tref = nap.Ts(flashes_test_white.start+.50),
minmax=(window_size)
)
# Re-center timestamps for predicted
peri_black_pred = nap.compute_perievent_continuous(
timeseries = predicted,
tref = nap.Ts(flashes_test_black.start+.50),
minmax=(window_size)
)
We can then plot the centered spikes in a PSTH! Let’s see how that looks for the first 9 units.
Show code cell source
def plot_pop_psth(
peri_color,
color_flashes,
bin_size,
smoothing=0.015,
n_units = 9,
**peri_others
):
"""
Plot perievent time histograms (PSTHs) and raster plots for multiple units.
Parameters:
-----------
peri_color : dict
Dictionary mapping unit names to binned spike count peri-stimulus data (e.g., binned time series).
units : dict
Dictionary of neural units, e.g., spike trains or trial-aligned spike events.
color_flashes : str
A label indicating the flash color condition ('black' or other), used for visual styling.
bin_size : float
Size of the bin used for spike count computation (in seconds).
smoothing : float
Standard deviation for Gaussian smoothing of the PSTH traces.
"""
# Layout setup: 7 columns (units), 2 rows (split vertically into PSTH and raster plot)
n_cols = n_units
n_rows = 1
fig, ax = plt.subplots(n_rows, n_cols)
fig.set_figheight(2.5)
fig.set_figwidth(17)
fig.tight_layout()
# Use tab20 color palette for plotting different units
colors = plt.cm.tab20.colors[:n_cols]
start = 0
end = n_rows # Plot as many units as half the number of rows
# each unit occupies 2 rows (one for psth and other for raster)
for i in range(n_units):
u = peri_color[:,:,i]
# Plot PSTH (smoothed firing rate)
if (i == 0):
ax[i].plot(
(np.mean(u, axis=1) / bin_size).smooth(std=smoothing),
linewidth=2,
color="black",
label = "Observed"
)
else:
ax[i].plot(
(np.mean(u, axis=1) / bin_size).smooth(std=smoothing),
linewidth=2,
color="black",
)
ax[i].axvline(0.0) # Stimulus onset line
span_color = "black" if color_flashes == "black" else "silver"
ax[i].axvspan(0, 0.250, color=span_color, alpha=0.3, ec="black") # Stim duration
ax[i].set_xlim(-0.25, 0.50)
ax[i].set_title(f'{i}')
for (label, color, peri_pred) in peri_others.values():
u_pred = peri_pred[:,:,i]
if (i == 0):
ax[i].plot(
(np.mean(u_pred, axis=1)),
linewidth=1.5,
color=color,
label = label
)
else:
ax[i].plot(
(np.mean(u_pred, axis=1)),
linewidth=1.5,
color=color,
)
# Shift window for next units
start += 1
end += 1
# Y-axis and title annotations
ax[0].set_ylabel("Rate (Hz)")
if n_rows > 2:
ax[2, 0].set_ylabel("Rate (Hz)")
ax[3, 0].set_ylabel("Trial")
fig.legend()
fig.text(0.5, 0.00, 'Time from stim(s)', ha='center')
fig.text(0.5, 1.00, f'PSTH - {color_flashes} flashes', ha='center')
plot_pop_psth(
peri_white_test,
"white",
bin_size,
peri_pred_stimuli = ("Predicted", "red", peri_white_pred)
)
plot_pop_psth(
peri_black_test,
"black",
bin_size,
peri_pred_stimuli = ("Predicted", "red", peri_black_pred)
)


The model does pretty good! However, we can see some artifacts and unnatural peaks. What could we try to improve this model a little bit?
Adding coupling as a new predictor#
We can try extending the model in order to improve its performance. There are many ways one can do this: the iterative refinement and improvement of your model is an important part of the scientific process! In this tutorial, we’ll discuss one such extension, but you’re encouraged to try others.
Now, we’ll extend the model by adding coupling terms—that is, including the activity of other neurons as predictors—to account for shared variability within the network. It’s been shown by Pillow et al. [2008] [1b] that spike times can be predicted more accurately when taking into account the spiking of neighbouring units.
We start by creating a new basis object
# New basis object for coupling
basis_coupling = nmo.basis.RaisedCosineLogConv(
n_basis_funcs=8, window_size=window_len, label="spike_history"
)
We can add this new basis to our old additive basis
# New additive basis with coupling term
additive_basis_coupling = additive_basis + basis_coupling
And use compute_features to convolve our input features with the basis object to compress them.
# Compute the features for train and test
X_coupling_train = additive_basis_coupling.compute_features(
np.asarray(white_train_on.d, dtype=float),
np.asarray(white_train_off.d, dtype=float),
np.asarray(predictors_train["white"], dtype=float),
np.asarray(black_train_on.d, dtype=float),
np.asarray(black_train_off.d, dtype=float),
np.asarray(predictors_train["black"], dtype=float),
np.asarray(units_counts_train.d, dtype=float),
)
X_coupling_test = additive_basis_coupling.compute_features(
np.asarray(white_test_on.d, dtype=float),
np.asarray(white_test_off.d, dtype=float),
np.asarray(predictors_test["white"], dtype=float),
np.asarray(black_test_on.d, dtype=float),
np.asarray(black_test_off.d, dtype=float),
np.asarray(predictors_test["black"], dtype=float),
np.asarray(units_counts_test.d, dtype=float),
)
What is the result of running compute_features with our raised cosine log-stretched basis and the spike counts?
compute_features is convolving all spike counts from all neurons with a raised cosine log-stretched basis. We do this because adding a coupling filter would resemble interactions between cells, and can mimic the effects of shared input noise, as mentioned in Pillow et al. [2008] [1c].
We initialize a new PopulationGLM object
regularizer_strength = 0.005
model_coupling = nmo.glm.PopulationGLM(
regularizer = "Ridge",
regularizer_strength = regularizer_strength,
solver_name="LBFGS"
)
Where did this new regularizer_strength value come from?
We conducted cross validation again to obtain the regularization strength for this new model. Adding extra parameters increases the risk of overfitting, so getting a new regularizer_strength to account for that makes sense.
from sklearn.model_selection import GridSearchCV
model_coupling = nmo.glm.PopulationGLM(
regularizer = "Ridge",
regularizer_strength = regularizer_strength,
solver_name="LBFGS"
)
# Create parameter grid
param_grid = {
"regularizer_strength" :
np.geomspace(10**-9, 10, 10)
}
# Instantiate the grid search object
grid_search = GridSearchCV(
model_coupling,param_grid,
cv=5
)
# Run grid search
grid_search.fit(X_coupling_train, units_counts_train)
# Print optimal parameter
print(grid_search.best_estimator_.regularizer_strength)
>>> 0.004641588833612782
Here we got a regularizer strength for the whole population but, again, when conducting a real analysis, a regularizer strength must be obtained for each unit.
And we fit calling model_coupling.fit()
model_coupling.fit(X_coupling_train,units_counts_train)
PopulationGLM(
observation_model=PoissonObservations(),
inverse_link_function=exp,
regularizer=Ridge(),
regularizer_strength=0.005,
solver_name='LBFGS'
)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| observation_model | PoissonObservations() | |
| inverse_link_function | <function exp...001D8FA7C84C0> | |
| regularizer | Ridge() | |
| regularizer_strength | 0.005 | |
| solver_name | 'LBFGS' | |
| solver_kwargs | {} | |
| feature_mask | None |
Assess coupling PopulationGLM performance: heatmap#
Another way to visually inspect how well our PopulationGLM model captures the neural responses is to summarize the activity from all the units using a heatmap. Here’s how we construct it:
Predict: we get the predicted firing rate of each timepoint for each neuron using
predictwith ourPopulationGLMmodel object.Re center timestamps: we can use Pynapple function
compute_perievent_continuousto re-center spiking activity timestamps around the presentation of stimuli.Z-scoring: We normalize the activity of each unit by converting it to z-scores. This removes differences in firing rate scale and allows us to focus on the relative response patterns across neurons.
Sorting by peak time: We then sort neurons by the time at which they show their peak response in the observed data. This reveals any sequential or structured dynamics in the population response. We sort the observed data, and then use that sorting to order the prediction.
Side-by-side comparison: Finally, we plot the observed and predicted population responses side by side. If the model captures the key features of the response, the predicted plot should resemble the observed one: we would expect to see a similar diagonal or curved band of activity, reflecting the ordered peak responses.
Step 1: The same way as before, we can obtain the predictions using predict
predicted = nap.TsdFrame(
t=units_counts_test.t,
d=np.asarray(model_coupling.predict(X_coupling_test), dtype=float) / bin_size,
time_support=units_counts_test.time_support
)
Step 2: we can center unit’s activity around stimuli presentation with compute_perievent_continuous
# Re-center timestamps for predicted
peri_white_pred_coupling = nap.compute_perievent_continuous(
timeseries = predicted,
tref = nap.Ts(flashes_test_white.start+.50),
minmax=(window_size)
)
peri_black_pred_coupling = nap.compute_perievent_continuous(
timeseries = predicted,
tref = nap.Ts(flashes_test_black.start+.50),
minmax=(window_size)
)
Steps 3 and 4: Z-scoring and sorting according to peak time
def create_zscore_dic(
peri_white_test,
peri_black_test,
peri_white_pred,
peri_black_pred,
smoothing = 0.015):
"""
Computes z-scored, time-aligned population responses for both observed
and predicted data and stores the outputs in separate dictionaries
For each stimulus condition (white, black), the function:
- Averages peri-stimulus time series across trials
- Restricts to a fixed time window around stimulus onset
- Applies z-scoring across time for each neuron
- Sorts neurons by time of peak response (in observed data)
- Returns sorted z-scored matrices for both and predicted data
Parameters
----------
peri_white_test : TsdFrame
Observed responses to white stimuli (trials × time × neurons).
peri_black_test : TsdFrame
Observed responses to black stimuli.
peri_white_pred : TsdFrame
Predicted responses to white stimuli.
peri_black_pred : TsdFrame
Predicted responses to black stimuli.
smoothing : float
Standard deviation for Gaussian smoothing of the perievent traces.
Returns
-------
dic_test : dict
Dictionary containing:
- 'z': z-scored and sorted observed activity (time × neurons)
- 'order': neuron sorting indices based on peak response
dic_pred : dict
Dictionary containing:
- 'z': z-scored predicted activity, sorted using test order
"""
# Time window around the stimulus (250 ms before and 500ms after)
restriction = [-.24, .5]
# Initialize dictionaries to store processed data
dic_test = {
"white": {"z": None, "order": None}, # Z-scored + sorted activity + sort order
"black": {"z": None, "order": None}
}
dic_pred = {
"white": {"z": None}, # Z-scored + sorted predicted activity
"black": {"z": None}
}
# Process TEST data for each stimulus type
for color, peri in zip(["white", "black"], [peri_white_test, peri_black_test]):
# Restrict time window and average across trials
mean_peri = np.mean(
peri.restrict(nap.IntervalSet(restriction)), axis=1
).smooth(std=smoothing)
# Z-score across time for each neuron (independently)
z_mean_peri = zscore(mean_peri, axis=0)
# Sort neurons by time of their peak response
order = np.argsort(np.argmax(z_mean_peri, axis=0))
# Apply sorting to z-scored data
z_sorted = z_mean_peri[:, order]
# Store results in dictionary
dic_test[color]["z"] = z_sorted
dic_test[color]["order"] = order
# Process PREDICTED data
for color, peri in zip(
["white", "black"],
[peri_white_pred, peri_black_pred]):
# Restrict time window and average across trials
mean_peri = np.mean(
peri.restrict(nap.IntervalSet(restriction)), axis=1
)
# Z-score across time for each neuron
z_mean_peri = zscore(mean_peri, axis=0)
# Use the same neuron ordering as in test data for comparison
order = dic_test[color]["order"]
# Sort predicted responses using test-data order
z_sorted = z_mean_peri[:, order]
# Store in dictionary
dic_pred[color]["z"] = z_sorted
return dic_test, dic_pred
Create our dictionaries of z-scored mean activity
dic_test, dic_pred_coupling = create_zscore_dic(
peri_white_test,
peri_black_test,
peri_white_pred_coupling,
peri_black_pred_coupling
)
dic_test, dic_pred_stimuli = create_zscore_dic(
peri_white_test,
peri_black_test,
peri_white_pred,
peri_black_pred)
Step 5: Plot side by side comparison
Show code cell source
def plot_zscores(dic_test, dic_pred_stimuli, dic_pred_coupling, bin_size = bin_size):
"""
Plot heatmaps of z-scored neuronal responses for both observed and predicted data.
For each stimulus type (white and black), the function:
- Plots a heatmap of z-scored activity for each unit, sorted by time of peak response
- Compares observed and predicted activity side-by-side
- Adds time markers at stimulus onset and offset
Parameters
----------
dic_test : dict
Dictionary with observed z-scored and sorted activity for 'white' and 'black' stimuli.
dic_pred : dict
Dictionary with predicted z-scored activity for 'white' and 'black' stimuli,
sorted using the same order as dic_test.
Returns
-------
None
Displays matplotlib figures.
"""
for color in ["white", "black"]:
fig, ax = plt.subplots(1, 3)
fig.tight_layout()
fig.set_figheight(4)
fig.set_figwidth(20)
# Number of time bins in z-scored matrix (time x neurons)
#num_bins = dic_test[color]["z"].shape[0]
# Create time axis assuming bin size defined elsewhere
time = np.arange(-0.24, 0.5, bin_size)
# Image limits: [x_min, x_max, y_min, y_max]
limits = [time[0], time[-1], 0, dic_test[color]["z"].shape[1]]
# Plot observed activity
im = ax[0].imshow(
np.array(dic_test[color]["z"]).T, # neurons on y-axis, time on x-axis
aspect="auto",
extent=limits
)
ax[0].set_title(f"{color.capitalize()} Observed")
# Plot predicted activity with stimuli model
im = ax[1].imshow(
np.array(dic_pred_stimuli[color]["z"]).T,
aspect="auto",
extent=limits
)
ax[1].set_title(f"{color.capitalize()} Predicted (Stimuli)")
# Plot predicted activity with coupling model
im = ax[2].imshow(
np.array(dic_pred_coupling[color]["z"]).T,
aspect="auto",
extent=limits
)
ax[2].set_title(f"{color.capitalize()} Predicted (Stimuli + Coupling)")
# Add vertical lines for stimulus onset (0s) and offset (0.25s)
for a in ax:
a.axvline(0.0, color='k', linestyle='--')
a.axvline(0.25, color='k', linestyle='--')
a.set_ylabel("Unit")
# Shared x-axis label
fig.text(0.45, 0.00, 'Time from stim (s)', ha='center')
# Colorbar
fig.colorbar(im, ax=ax, location='right', label='Z-score')
plt.show()
plot_zscores(dic_test, dic_pred_stimuli, dic_pred_coupling)
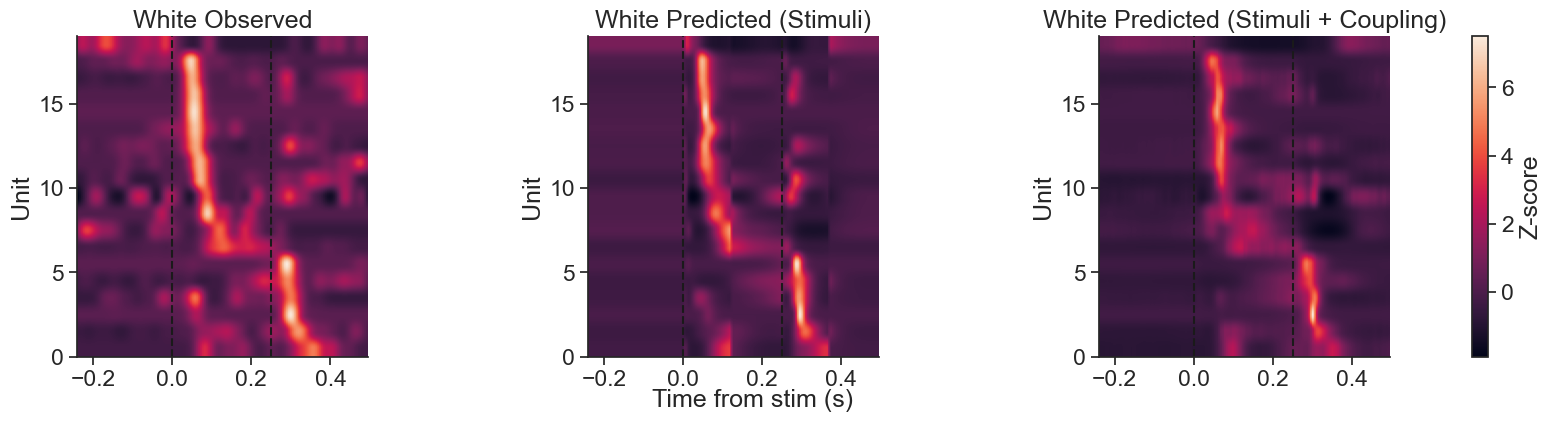
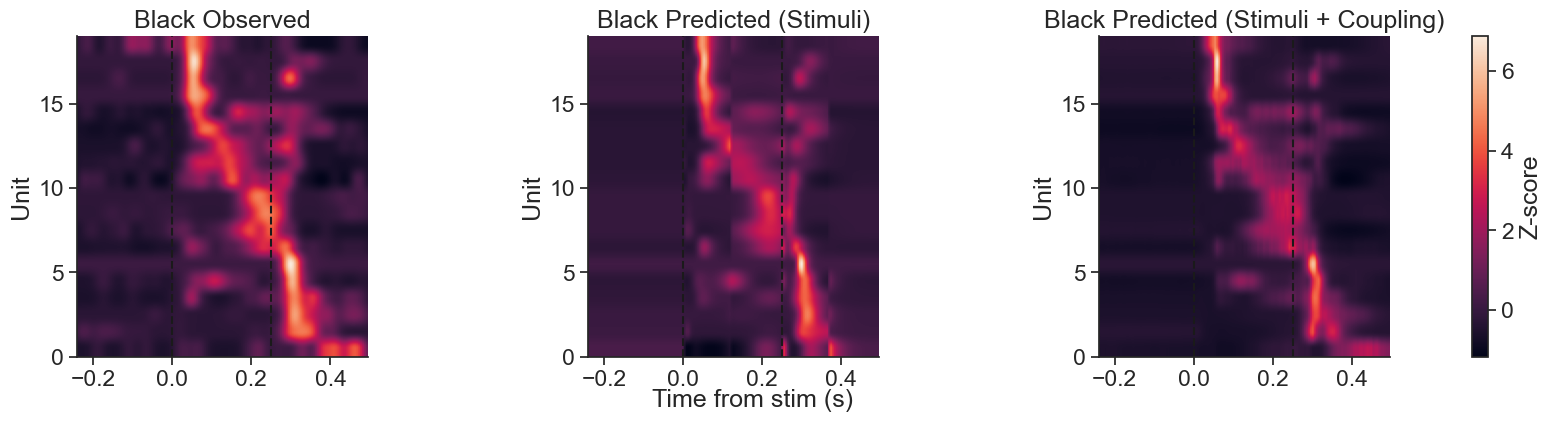
To the left of this plot we can see the observed z-scored activity, sorted by peak response time. In the middle, we can see the z-scored predictions of the model with Stimuli filters. To the right, we can see the z-scored predictions of the model with Stimuli and Coupling filters.
We can see that the average peak activity looks similar! Let’s compare the prediction of the Stimuli versus the Stimuli + Coupling model using a PSTH:
plot_pop_psth(
peri_white_test,
"white",
bin_size,
peri_pred_stimuli = ("Stimuli", "red", peri_white_pred),
peri_pred_coupling = ("Stimuli + Coupling", "blue", peri_white_pred_coupling)
)
plot_pop_psth(
peri_black_test,
"black",
bin_size,
peri_pred_stimuli = ("Stimuli", "red", peri_black_pred),
peri_pred_coupling = ("Stimuli + Coupling", "blue", peri_black_pred_coupling)
)


Evaluate model performance quantitatively: Pseudo-\(R^2\) McFadden#
Comparing the two models by examining their predictions is important, but you may also want a number with which to evaluate and compare your models’ performance. As discussed earlier, the GLM optimizes log-likelihood to find the best-fitting weights, and we can calculate this number using NeMoS score method.
This function takes the following as required inputs:
Predictors (in our case, our additive basis
X_coupling_test, which includes information of our black and white predictors, as well as the subset of units counts corresponding to the test set)Counts (in our case,
units_counts_test, because we wish to evaluate how good the model is at predicting unseen data)
By default, score computes the mean log-likelihood. However, because the log-likelihood is un-normalized, it should not be compared across datasets (because e.g., it won’t account for difference in noise levels). We provide the ability to compute the pseudo-\(R^2\) for this purpose. For that, you only need to pass "pseudo-r2-McFadden" as score_type (optional input):
Why are we using pseudo-r2? Why not just use standard \(R^2\) as in linear regression?
In standard linear regression, model performance is often evaluated using the coefficient of determination, \(R^2\), which represents the proportion of variance in the data explained by the model:
Here:
The numerator is the residual sum of squares (variance not explained by the model),
The denominator is the total variance of the observations.
For instance, if a model only predicts the mean of the data (i.e., \(\hat{y}_i = \mu\) for all \(i\)), then:
This means the model explains none of the variance beyond the baseline.
However, for GLMs, using \(R^2\) is problematic for two key reasons:
Mean-variance relationship: in many GLMs, the variance is not constant but depends on the mean. For example, in a LNP model, a higher predicted firing rate implies a higher variance. This violates the assumption of homoscedasticity (constant variance) required for standard \(R^2\) to be meaningful. As a result, even a model that predicts the mean accurately might appear to perform poorly under \(R^2\) due to large, but expected, residuals.
Nonlinear link function: GLMs include a nonlinear transformation (link function) between the predictors and the mean of the observations. Because \(R^2\) is derived under the assumption of a linear relationship, it no longer reflects the “proportion of explained variance” in a meaningful way when this assumption is violated.
To address these limitations, we use pseudo-r2, which generalizes the concept of goodness-of-fit to non-Gaussian models. One common version is McFadden’s pseudo-\(R^2\), defined as:
Where:
\(\log L_M\) is the log-likelihood of the fitted model,
\(\log L_0\) is the log-likelihood of the null model (a model with only an intercept, i.e. predicting a constant mean).
This metric captures how much better the model is compared to simply predicting a constant mean, and can be interpreted as a normalized log-likelihood. Its values typically range between 0 and 1, but negative values can occur and may indicate poor fit or overfitting.
In this tutorial, we use McFadden’s pseudo-\(R^2\) to evaluate model performance, as it is more appropriate for models like the LNP model used here.
For more details on implementation and additional scoring metrics, see the NeMos documentation.
# Calculate the mean score for the Stimuli + Coupling model
# using pseudo-r2-McFadden
score_coupling = model_coupling.score(
X_coupling_test,
units_counts_test,
score_type = "pseudo-r2-McFadden"
)
print(score_coupling)
0.19474232
We can also access each unit’s score by adding a lambda function to the optional parameter aggregate_sample_scores
# Obtain individual units' scores
score_units = model_coupling.score(
X_coupling_test,
units_counts_test,
score_type = "pseudo-r2-McFadden",
aggregate_sample_scores=lambda x:np.mean(x,axis=0),
)
print(score_units)
[0.10401607 0.41909814 0.16163844 0.10189188 0.17063117 0.5848063
0.2437715 0.1242221 0.090765 0.03999352 0.17067832 0.1294164
0.08004951 0.1682806 0.26983613 0.17280346 0.3971427 0.12376541
0.4043957 ]
Let’s calculate the score separately for white and black flashes, and for both models (Stimuli and Stimuli + Coupling) using helper functions
Show code cell source
def evaluate_model(model, X, y, score_type="pseudo-r2-McFadden"):
"""
Evaluate a model's performance at the population and unit levels.
Parameters
----------
model : object
A model object that implements a `.score()` method with arguments `X`, `y`, and `score_type`.
X : array-like or pynapple-compatible object
Input features used for evaluation.
y : array-like or pynapple-compatible object
Target outputs corresponding to `X`.
score_type : str, optional
The scoring metric to use (e.g., "log-likelihood" or "pseudo-r2-McFadden"). Passed to the model's `score` method.
Returns
-------
score_pop : float
The population-level score (aggregated across all units and samples).
score_unit : np.ndarray
The unit-level scores, computed by averaging over samples for each unit.
"""
score_pop = model.score(
X,
y,
score_type=score_type,
)
score_unit = model.score(
X,
y,
aggregate_sample_scores=lambda x: np.mean(x, axis=0),
score_type=score_type,
)
return score_pop, score_unit
def evaluate_models_by_color(models, X_sets, y_sets, flashes_color, score_type="log-likelihood"):
"""
Evaluate multiple models on a dataset filtered by flash color.
Parameters
----------
models : dict of str -> model
Dictionary of model names and model objects to evaluate. Each model must implement `.score()`.
X_sets : dict of str -> array-like or pynapple-compatible object
Dictionary mapping model names to their corresponding input features.
y_sets : array-like or pynapple-compatible object
The target outputs to be used with all models.
flashes_color : str
The flash color condition used to restrict the data (e.g., "black" or "white").
score_type : str, optional
The scoring metric to use (e.g., "log-likelihood").
Returns
-------
model_base_pop : float
Population-level score of the first model in `models`.
model_base_unit : np.ndarray
Unit-level scores of the first model in `models`.
model_hist_pop : float
Population-level score of the second model in `models`.
model_hist_unit : np.ndarray
Unit-level scores of the second model in `models`.
Notes
-----
The function assumes exactly two models in the `models` dictionary,
and returns their scores in fixed order based on insertion into the dictionary,
first returning the population score, then the unit scores for each.
"""
models_list = []
for model_name, model in models.items():
y = y_sets.restrict(flashes_color)
X_raw = X_sets[model_name]
if hasattr(X_raw, "restrict"):
X = X_raw.restrict(flashes_color)
else:
X = np.asarray(X_raw)[np.isin(np.asarray(y_sets.t), np.asarray(y.t))]
models_list.append(evaluate_model(model, X, y, score_type))
return models_list[0][0], models_list[0][1], models_list[1][0], models_list[1][1]
# Define model dictionary
models = {
"stimuli": model_stimuli,
"coupling": model_coupling
}
# Calculate scores when predicting during white flashes
(score_white_stimuli_pop,
score_white_stimuli_unit,
score_white_coupling_pop,
score_white_coupling_unit) = evaluate_models_by_color(
models,
{"stimuli": X_test,
"coupling": X_coupling_test},
units_counts_test,
flashes_test_white,
"pseudo-r2-McFadden"
)
# Calculate scores when predicting during black flashes
(score_black_stimuli_pop,
score_black_stimuli_unit,
score_black_coupling_pop,
score_black_coupling_unit) = evaluate_models_by_color(
models,
{"stimuli": X_test,
"coupling": X_coupling_test},
units_counts_test,
flashes_test_black,
"pseudo-r2-McFadden"
)
We can also see the individual scores for each unit!
Show code cell source
def half_violin(ax, data, center, side="left", color="blue", width=0.3, alpha=1):
"""Draw a half violin on a matplotlib Axes."""
kde = gaussian_kde(data)
x = np.linspace(min(data), max(data), 200)
y = kde(x)
y = y / y.max() * width # normalize
if side == "left":
ax.fill_betweenx(x, center, center - y, facecolor=color, alpha=alpha, edgecolor="black")
elif side == "right":
ax.fill_betweenx(x, center, center + y, facecolor=color, alpha=alpha, edgecolor="black")
def plot_half_violin_scores():
# Data
stim_white = score_white_stimuli_unit
coupling_white = score_white_coupling_unit
stim_black = score_black_stimuli_unit
coupling_black = score_black_coupling_unit
positions = [0, 1]
labels = ["White", "Black"]
width = 0.3
num_units = len(stim_white)
fig, ax = plt.subplots(figsize=(10, 5))
# Plot violins
half_violin(ax, stim_white, center=positions[0], side="left", color="#1f77b4", width=width)
half_violin(ax, coupling_white, center=positions[0], side="right", color="#ff7f0e", width=width)
half_violin(ax, stim_black, center=positions[1], side="left", color="#1f77b4", width=width)
half_violin(ax, coupling_black, center=positions[1], side="right", color="#ff7f0e", width=width)
# Plot individual data points and connect within-color models
for i in range(num_units):
jitter = np.random.normal(scale=0.01)
# White
ax.plot([positions[0]-0.05+jitter, positions[0]+0.05+jitter],
[stim_white[i], coupling_white[i]],
color="gray", alpha=0.8, linewidth=0.8)
ax.scatter([positions[0]-0.05+jitter, positions[0]+0.05+jitter],
[stim_white[i], coupling_white[i]],
color="black", s=8, alpha=.3)
# Black
ax.plot([positions[1]-0.05+jitter, positions[1]+0.05+jitter],
[stim_black[i], coupling_black[i]],
color="gray", alpha=.8, linewidth=0.8)
ax.scatter([positions[1]-0.05+jitter, positions[1]+0.05+jitter],
[stim_black[i], coupling_black[i]],
color="black", s=8, alpha=.3)
# Plot mean markers and annotate with values
offset = 0.07
mean_kwargs = dict(marker='d', color="black", markersize=6, zorder=3)
def annotate_mean(x, y):
ax.plot(x, y, **mean_kwargs)
ax.text(x, y + 0.005, f"{y:.3f}", ha='center', va='bottom', fontsize=9)
annotate_mean(positions[0] - offset, np.mean(stim_white))
annotate_mean(positions[0] + offset, np.mean(coupling_white))
annotate_mean(positions[1] - offset, np.mean(stim_black))
annotate_mean(positions[1] + offset, np.mean(coupling_black))
# Axes formatting
ax.set_xticks(positions)
ax.set_xticklabels(labels)
ax.set_ylabel("Pseudo-$R^2$ McFadden")
ax.set_title("Unit Scores per Flash Color and Model Type")
# Legend
legend_elements = [
Patch(facecolor="#1f77b4", edgecolor='black', label="Stimuli"),
Patch(facecolor="#ff7f0e", edgecolor='black', label="Stimuli + Coupling")
]
ax.legend(
handles=legend_elements,
title="Model",
loc='upper left',
fontsize=9,
title_fontsize=10,
bbox_to_anchor=(.8, .2),
borderaxespad=0.
)
plt.tight_layout()
plt.show()
plot_half_violin_scores()
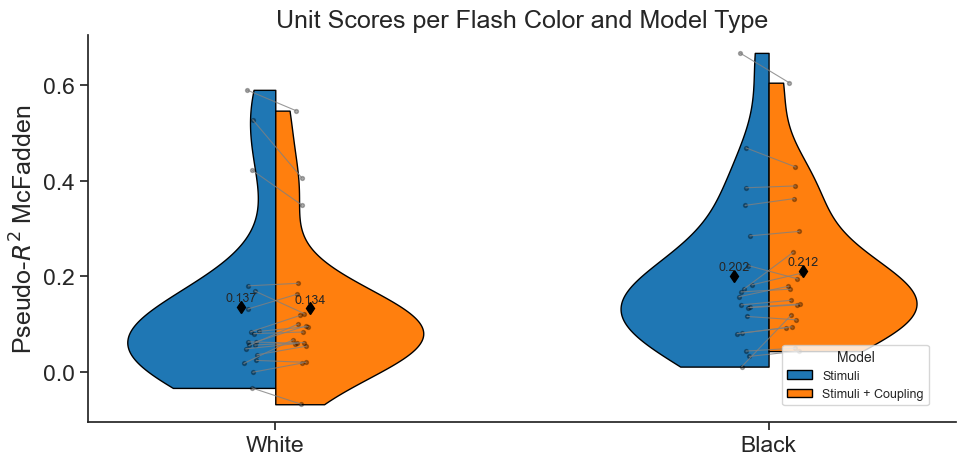
Although there is some variability between neurons, in general, the Stimuli + Coupling model is better at predicting spike trains than the model which only includes Stimuli filters. This makes a lot of sense! Noise is shared across neurons, and the information of a single cell response is also encoded in the population activity, beyond the information provided by stimuli alone Pillow et al. (2008) [1].
Food for thought#
We intentionally left out many details in this tutorial, as including everything would have resulted in a longer and more complex notebook. Our main goal was to introduce the key components of GLMs, walk through a real-data example, and demonstrate how using NeMoS and Pynapple can greatly simplify the modeling process. While going into every detail of model fitting was beyond the scope of this tutorial, it should not be beyond the scope of your own work. When applying GLMs to your own research questions, it’s crucial to be rigorous and intentional in your modeling choices.
In particular:
Explore different ways to split your data. Here, we used train and test data, but you could also try train, validate and test - specially if you will be trying different models and tweaking parameters before finally assessing the performance. Furthermore, different splitting strategies may be needed for different input statistics. For example, picking samples in a random uniform manner may be ideal for independent samples, but not recommended for time series (for which samples close in time are likely highly correlated).
Cross-validate the regularizer strength for each neuron individually, as using a fixed value across the population may lead to suboptimal fits. For example, the regularizer we used here does a reasonable job at capturing the activity of neurons that are strongly modulated by the flash (see units 1 and 5 in the PSTH of the Stimuli model). However, for neurons with weaker modulation (i.e., smaller changes in firing rate), the model tends to produce flattened predictions, possibly due to over-regularization (see units 4 or 3 in the PSTH of the Stimuli model).
Think carefully about and cross-validate the basis functions parameters, including the type of basis and the number of components. These choices can greatly influence the model’s performance, and it is important to remember that the basis of choice will force assumptions in your data, so it is key to be aware of those. For example, the raised cosine log stretched basis assumes that the precision of the basis decreases with the distance from the event. This makes the basis great to model rapid changes of the firing rate just after an event, and slow decay back to baseline. This may or may not be the case depending on the dynamics of the neuron you want to fit. There is a helpful NeMoS notebook on the topic dedicated to tuning basis functions — we encourage you to check it out.
We made one specific improvement to our model, i.e. adding coupling filters - what do you think would be another reasonable improvement to add? (hint: Pillow et al. [2008] [1d])
References#
[1a] [1b] [1c] [1d] Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, A. M., Chichilnisky, E. J., & Simoncelli, E. P. (2008). Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature, 454(7207), 995-999. https://doi.org/10.1038/nature07140
[2] Allen Institute for Brain Science. Allen Brain Observatory - Neuropixels Visual Coding - Technical White paper. Technical Report, Allen Institute for Brain Science, October 2019.
[3] Pillow, J. [Cosyne Talks]. (2018, March 1-4) Jonathan Pillow - Tutorial: Statistical models for neural data - Part 1 (Cosyne 2018) [Video]. Youtube
[4] Pillow, J. W., Paninski, L., Uzzell, V. J., Simoncelli, E. P., & Chichilnisky, E. J. (2005). Prediction and decoding of retinal ganglion cell responses with a probabilistic spiking model. The Journal of neuroscience : the official journal of the Society for Neuroscience, 25(47), 11003–11013. https://doi.org/10.1523/JNEUROSCI.3305-05.2005
Data citation#
The data used in this tutorial is from the Allen Brain Map, with the following citation:
Dataset: Allen Institute MindScope Program (2019). Allen Brain Observatory – Neuropixels Visual Coding [Dataset]. Available from brain-map.org/explore/circuits
Primary publication: Siegle, J. H., Jia, X., Durand, S., et al. (2021). Survey of spiking in the mouse visual system reveals functional hierarchy. Nature, 592(7612), 86-92. https://doi.org/10.1038/s41586-020-03171-x
Resources#
We have left some resources here and there throughout the notebook. Here is a complete list of all of them:
NeMoS GLM tutorial: for a bit more detailed explanation of all the components of a GLM within the NeMoS framework, as well as some nice visualizations of all the steps of the input transformation!
Introduction to GLM - CCN software workshop by the Flatiron Institute: for a step by step example of using GLMs to fit the activity of a single neuron in VISp under current injection.
Neuromatch Academy GLM tutorial: for a bit more detailed explanation of the components of a GLM, slides and some coding exercises to ensure comprehension.
Jonathan Pillow’s COSYNE tutorial: for a longer tutorial of all of the components of a GLM, as well as different types of GLM besides LNP
NeMoS Fit GLMs for neural coupling tutorial: for a guide on how to build a design matrix using raw history as a predictor, in the context of setting up a fully coupled GLM to capture pairwise interaction between neurons.
NeMoS fit head-direction population tutorial: for a step by step explanation of how to build the design matrix first as a result of convolving the features with the identity matrix, and then by using basis functions, alongside nice visualizations.
Flatiron Institute Introduction to GLMs tutorial: for a detailed explanation, step by step, on how predictors look with and without basis functions, with nice visualizations as well.
NeMoS notebook on composition of basis functions: for a detailed explanation of the different operations that can be carried out using basis functions in 2 and more dimensions.
Bishop, 2009: Section 3.1 for a formal description of what basis functions are and some examples of them.
NeMoS notebook on causal, anti-causal and acausal filters: for more information on the convolution occurring with basis functions, and how you can tailor that to your needs.
NeMoS notebook on conducting cross validation for bases: for a detailed explanation of how to combine NeMos objects within a scikit-learn pipeline to select the number of bases and bases type using cross validation.



